Конвективная диффузия к твердой частице • Обтекание сферической частицы стоксовым потоком • Диффузия к падающей твердой частице
Обтекание сферической частицы стоксовым потоком Рассмотрим обтекание твердой сферической частицы радиуса а однородным поступательным стоксовым потоком со скоростью U и вязкостью μ. В сферической системе координат исходные уравнения принимают вид: где
Обтекание сферической частицы стоксовым потоком Граничные условия на поверхности сферы: vr=vθ=0 при R=a. Условия на бесконечности: vr→ U cos θ , v θ → – U sin θ при R→∞ Компоненты скорости жидкости выражаются через функцию тока: Подставляя эти зависимости в уравнения движения получаем уравнения для функции тока: Решение: Где А, В, С, D- произвольные постоянные, Jn - функция Гегенбауера
Обтекание сферической частицы стоксовым потоком Используя граничные условия и ограничиваясь первым членом разложения получаем Отсюда компоненты скорости и давление: где Р – невозмущенное давление вдали от частицы.
Диффузия к падающей твердой частице Пусть частица настолько мала, что соответствующее число Рейнольдса Rе = Ua/ (где U — скорость падения и а — размер частицы) <<1, и Pe. D=Uа/D>>1. Режим движения бинарного раствора вокруг частицы вязкий, и распределение скоростей вблизи падающей частицы определяется по формуле Стокса. Уравнение конвективной диффузии в пограничном слое в сферических координатах г и имеет вид: Решение уравнения конвективной диффузии ищется при значениях r, близких к радиусу частицы а. (y=r-a; y/a<<1) (Из решения задачи о стоксовом обтекании шара)
Диффузия к падающей твердой частице Соответственно компоненты скорости выражаются через функцию тока: Уравнение диффузии запишем в переменных Ψ, θ. Для этого представим При малых значениях у (у<< а)
Диффузия к падающей твердой частице Уравнение конвективной диффузии в переменных ( , ) перепишется в виде Подставляя v , получаем: Граничные условия: с=0 при = 0 (на поверхности частицы), с = с0 при > (вдали от поверхности частицы), с = с0 при = 0, = 0. Введем новую переменную
Диффузия к падающей твердой частице Уравнение диффузии преобразуется к виду: Это уравнение имеет автомодельное решение вида с=с(η), Имеем
Диффузия к падающей твердой частице Уравнение диффузии в полных производных Произведя замену получаем Решение последнего уравнения где Из граничного условия на поверхности частицы С 3=0, из условия на бесконечности
Диффузия к падающей твердой частице Из условия в точке набегания потока на частицу = 0 концентрация с должна быть однозначной положительной функцией угла . При малых sin(2θ) разлагается в ряд и z определяется Для выполнения условия с=с0 при θ=0 необходимо, чтобы С 1=0. Следовательно. Диффузионный поток на поверхности частицы
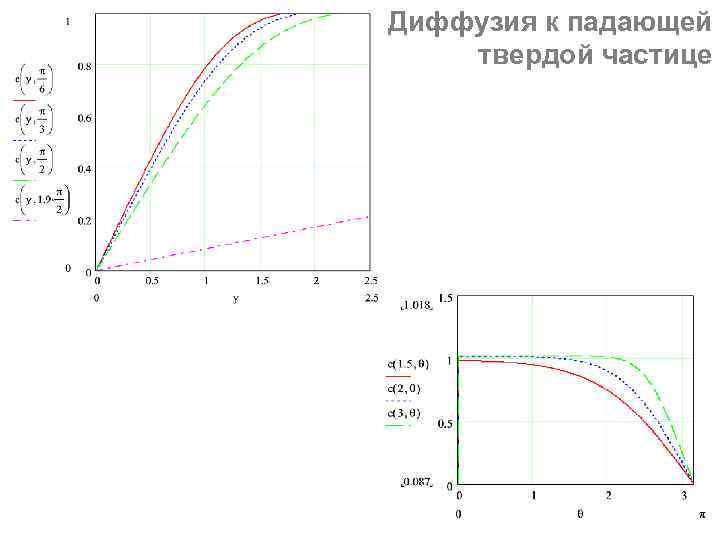
Диффузия к падающей твердой частице
Диффузия к падающей твердой частице Толщина диффузионного слоя имеет вид: Полный поток I вещества на частицу: I=7, 98 c 0 D 2/3 U 1/3 a 4/3 При Pe. D(=Ua/D)<<1 перенос вещества к сфере происходит за счет чистой диффузии, а конвективным потоком можно пренебречь. Уравнение диффузии преобразуется D с=0. Распределение концентрации зависит только от радиуса, т. е.
Диффузия к падающей твердой частице Граничные условия: с=0 при r=а, с=с0 при r→∞. Решение: c=c 0(1 -(a/r)2). Диффузионный поток на поверхность сферы Полный поток на частицу в случае Pe. D<<1 I = 4 π D a c 0 Можно написать апроксимационную формулу: I = 4 π D a c 0(1+0. 64*Pe 1/3).
Скачать презентацию Конвективная диффузия к твердой частице • Обтекание сферической
Лекция9_ дополнение.ppt