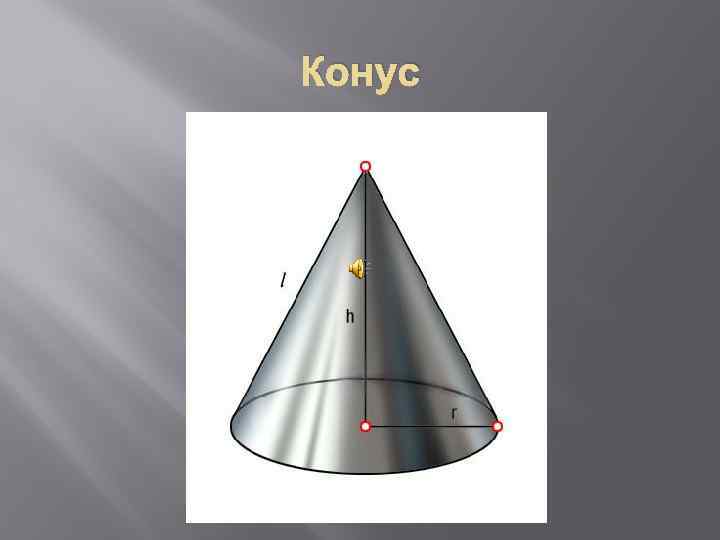
 Конус
Конус
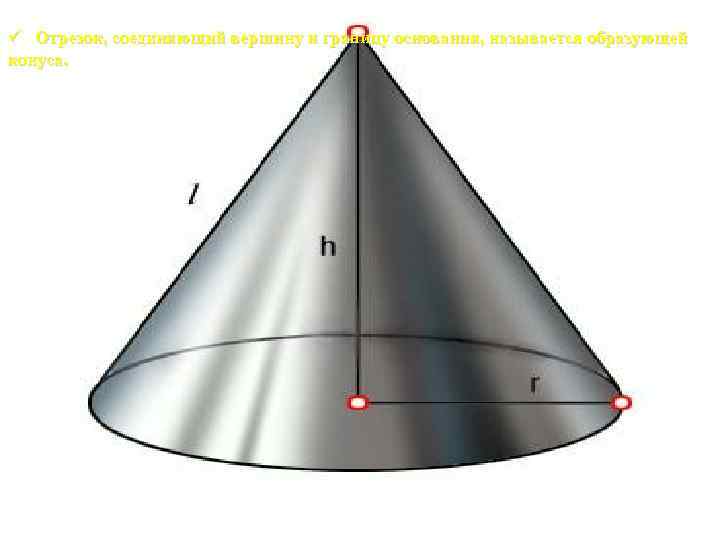 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
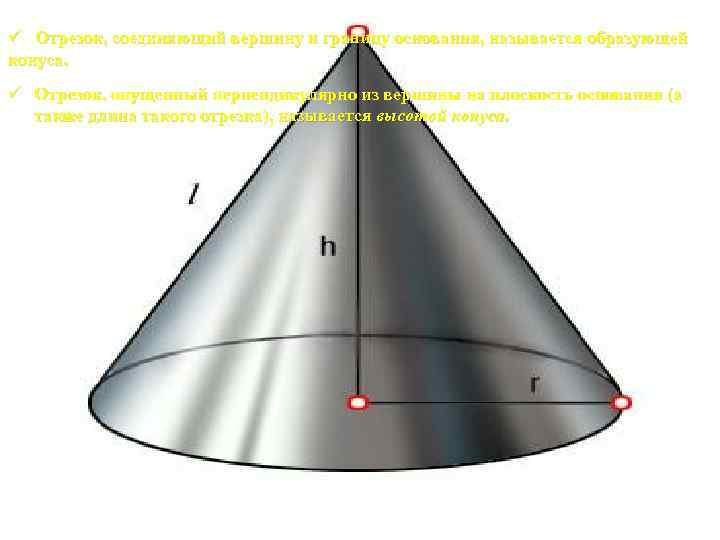 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
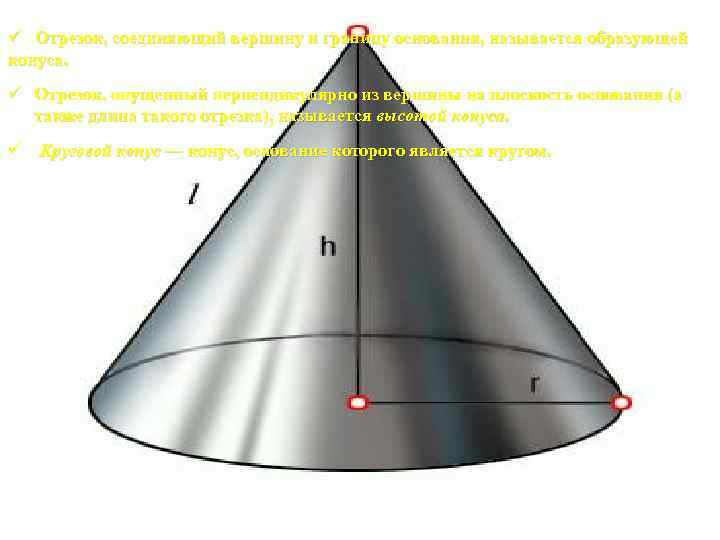 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом.
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом.
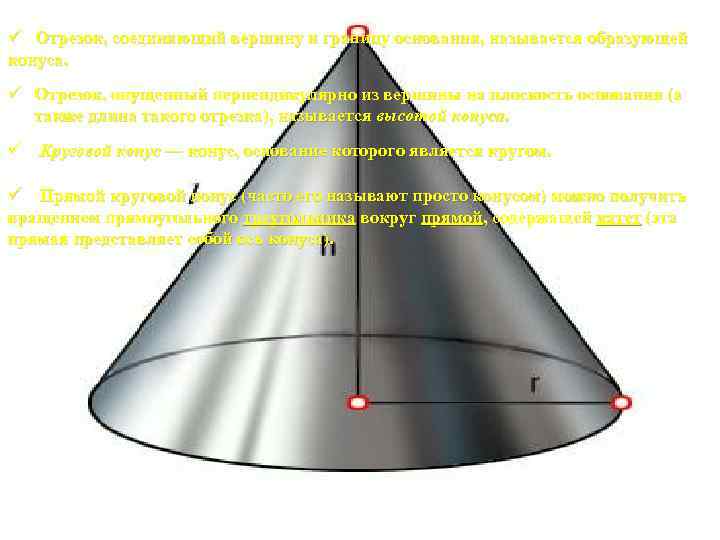 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
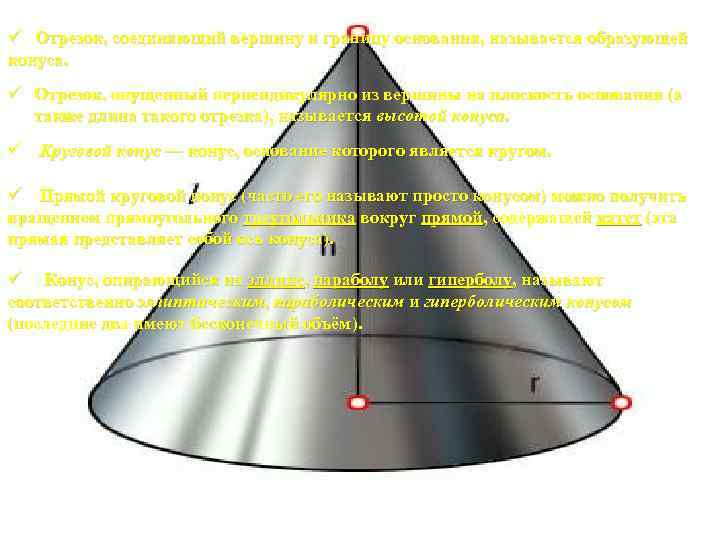 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса). ü Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса). ü Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
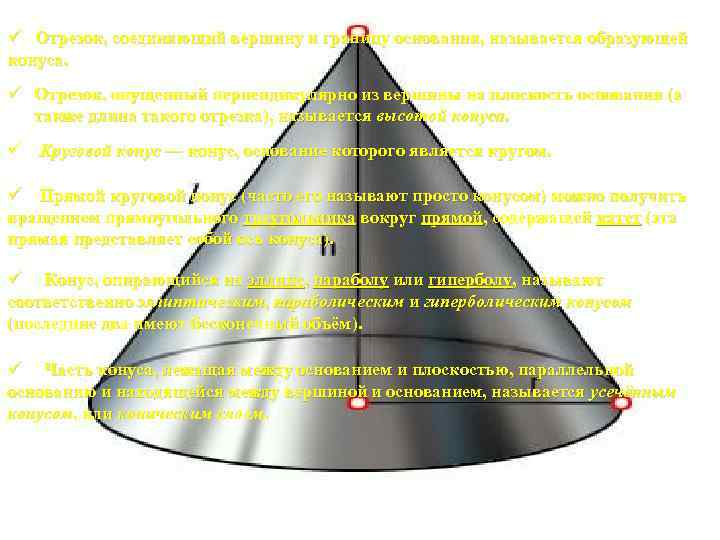 ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса). ü Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём). ü Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
ü Отрезок, соединяющий вершину и границу основания, называется образующей конуса. ü Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса. ü Круговой конус — конус, основание которого является кругом. ü Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса). ü Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём). ü Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
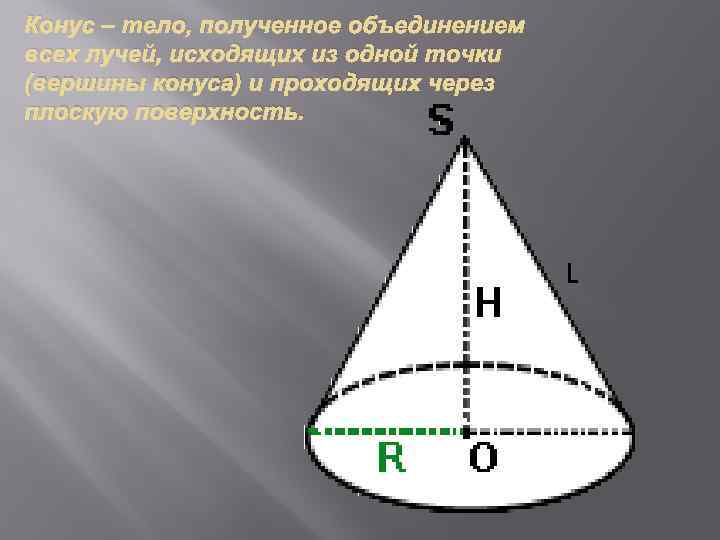 Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
 Как найти объем конуса ?
Как найти объем конуса ?
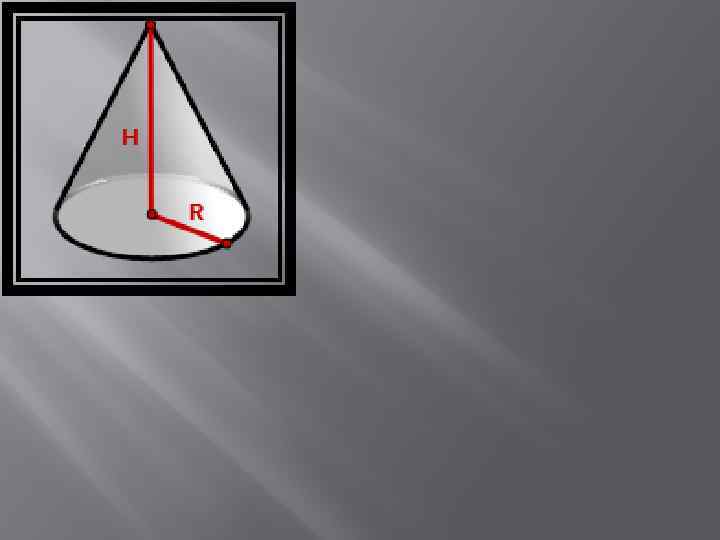
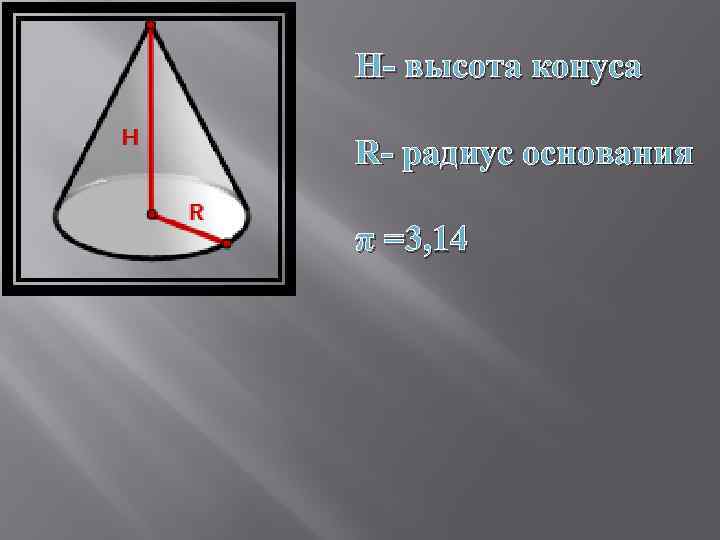 H- высота конуса R- радиус основания π =3, 14
H- высота конуса R- радиус основания π =3, 14
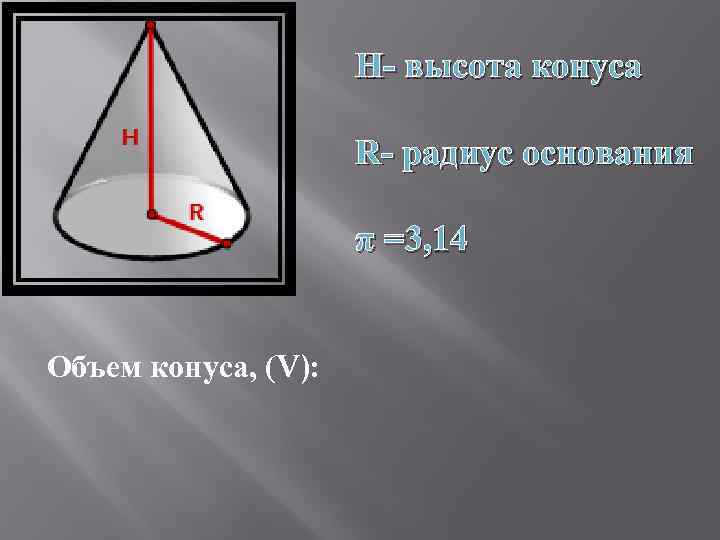 H- высота конуса R- радиус основания π =3, 14 Объем конуса, (V):
H- высота конуса R- радиус основания π =3, 14 Объем конуса, (V):
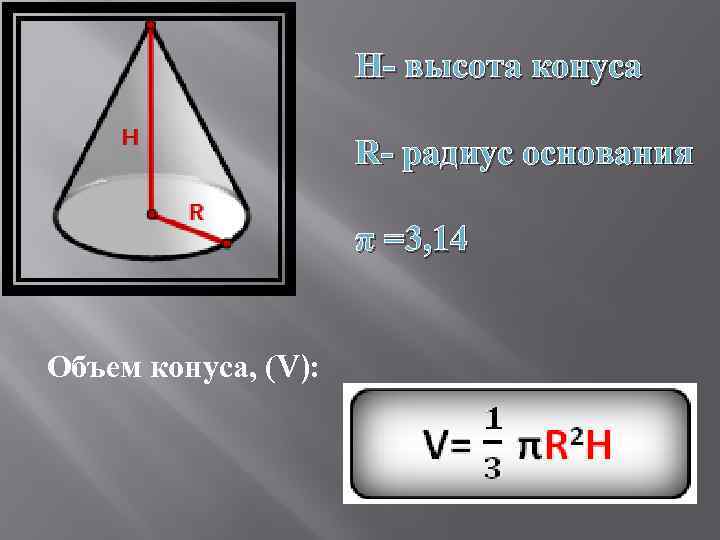 H- высота конуса R- радиус основания π =3, 14 Объем конуса, (V):
H- высота конуса R- радиус основания π =3, 14 Объем конуса, (V):
 Формула объема усеченного конуса
Формула объема усеченного конуса
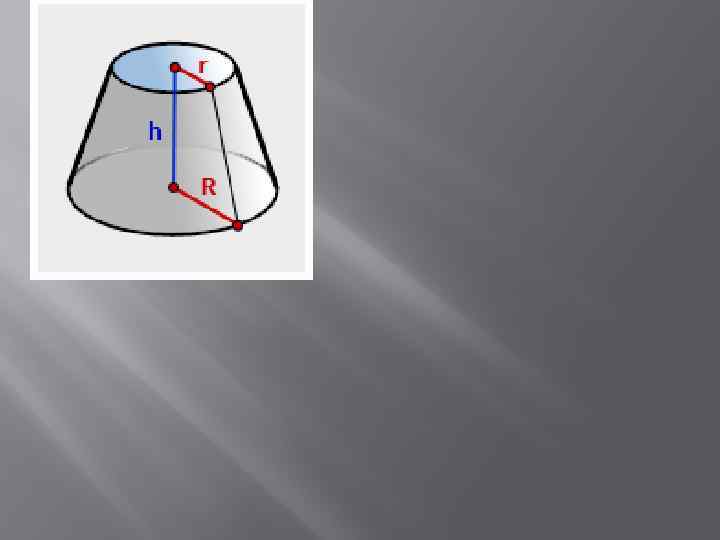
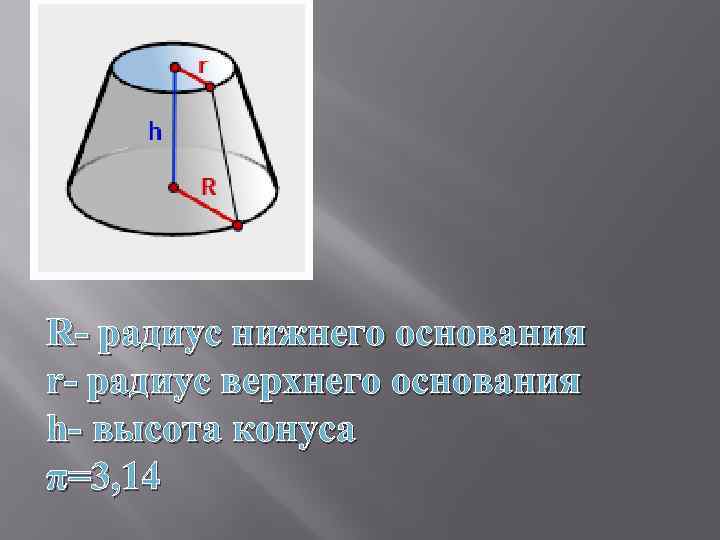 R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
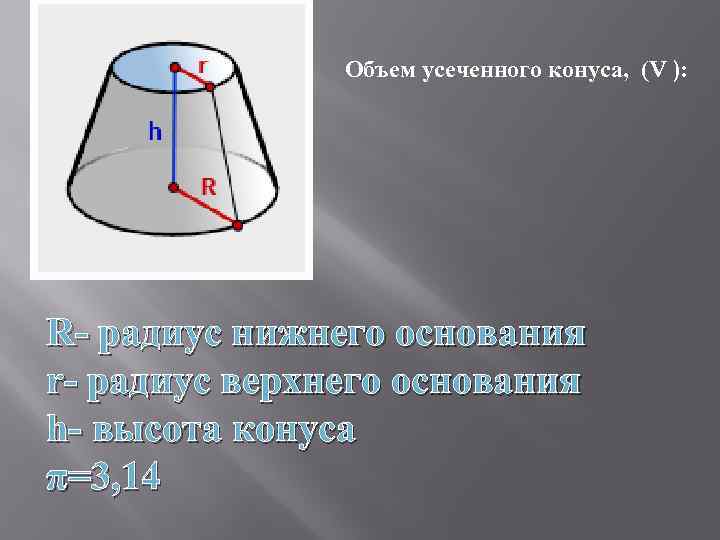 Объем усеченного конуса, (V ): R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
Объем усеченного конуса, (V ): R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
 Объем усеченного конуса, (V ): R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
Объем усеченного конуса, (V ): R- радиус нижнего основания r- радиус верхнего основания h- высота конуса π=3, 14
 Площадь поверхности прямого, кругового конуса
Площадь поверхности прямого, кругового конуса
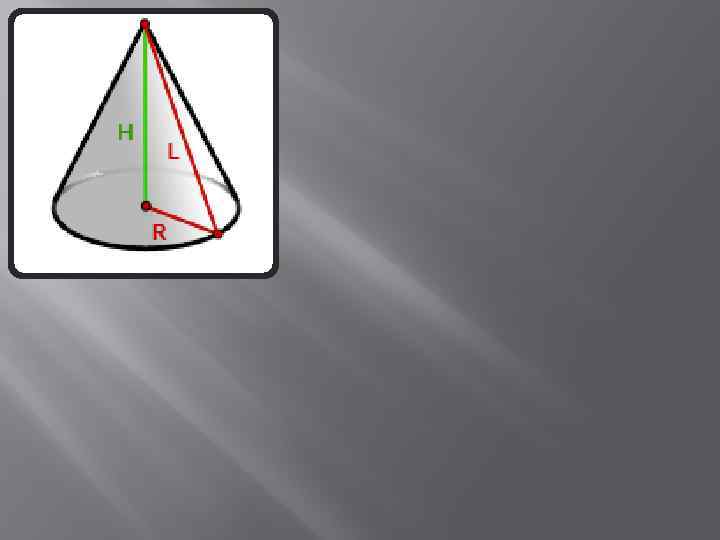
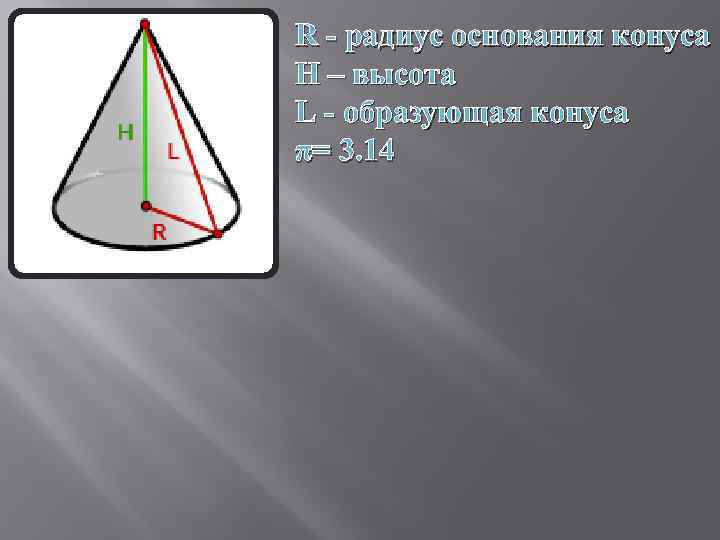 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14
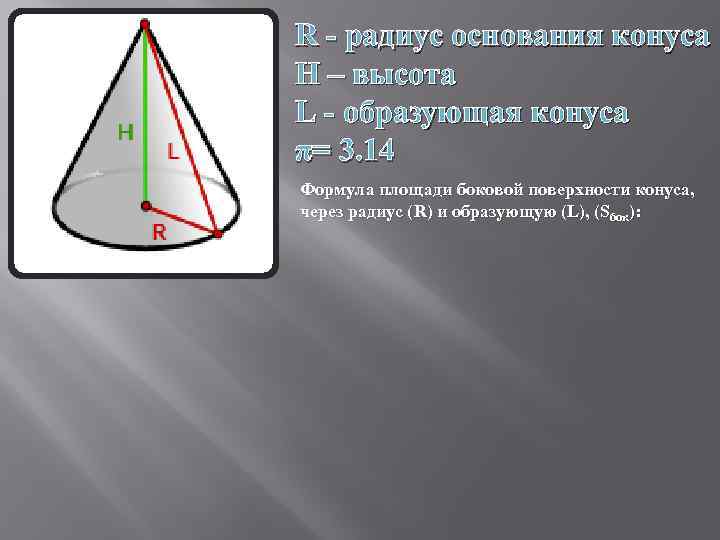 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
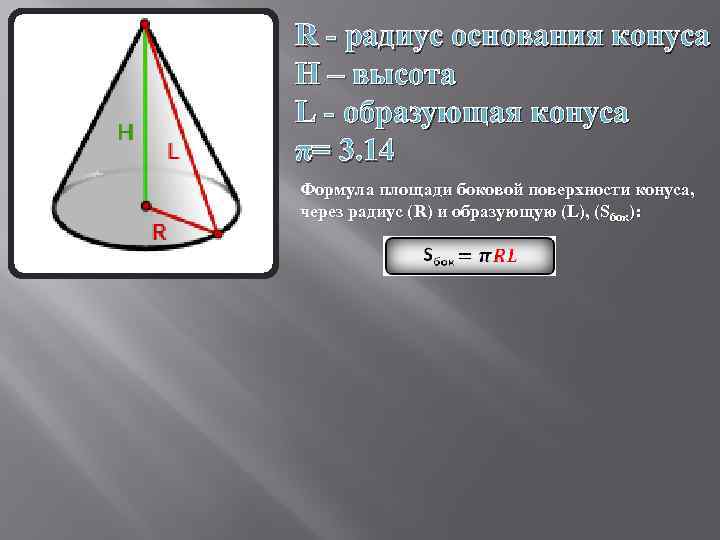 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
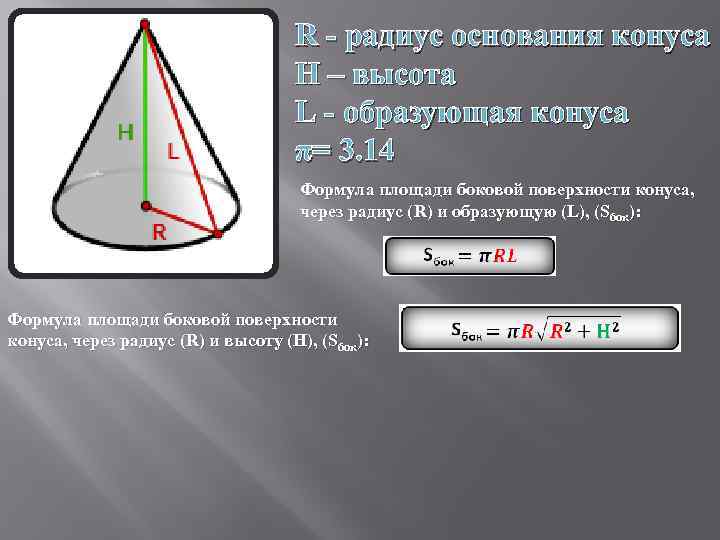
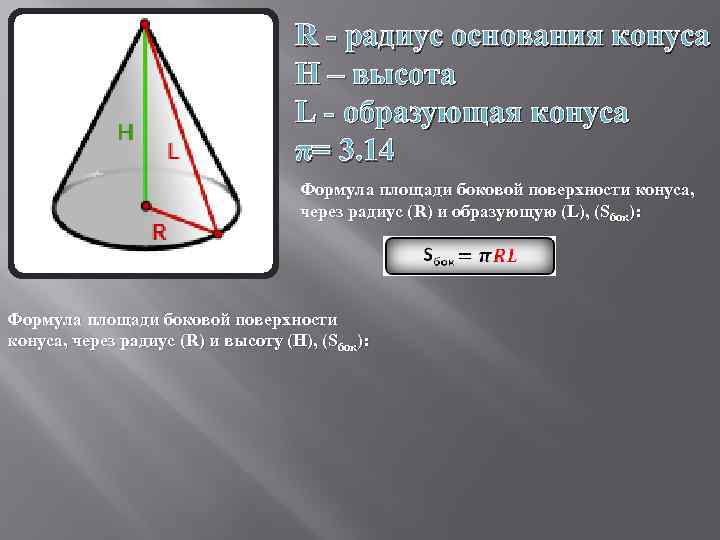 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
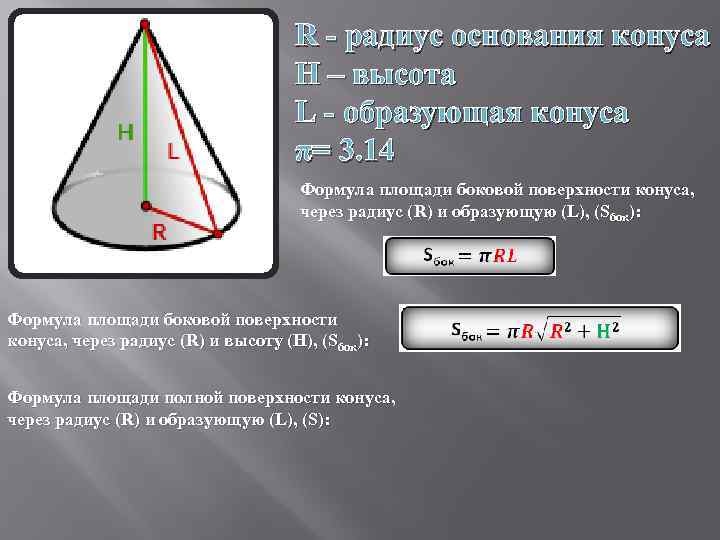 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
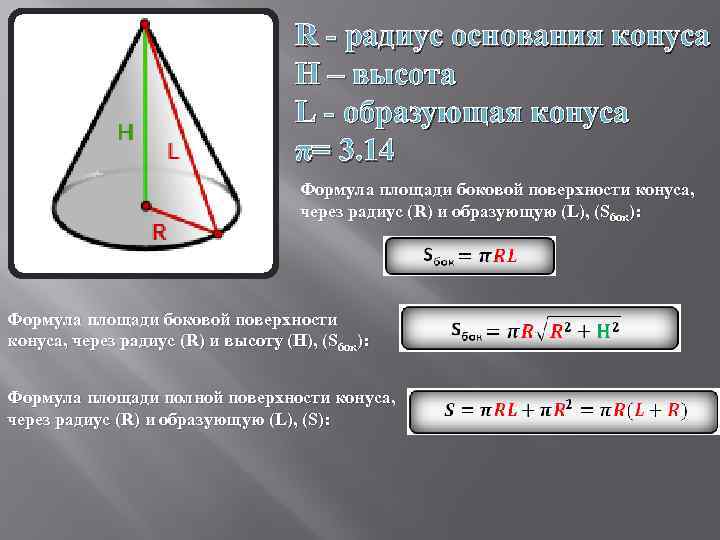 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
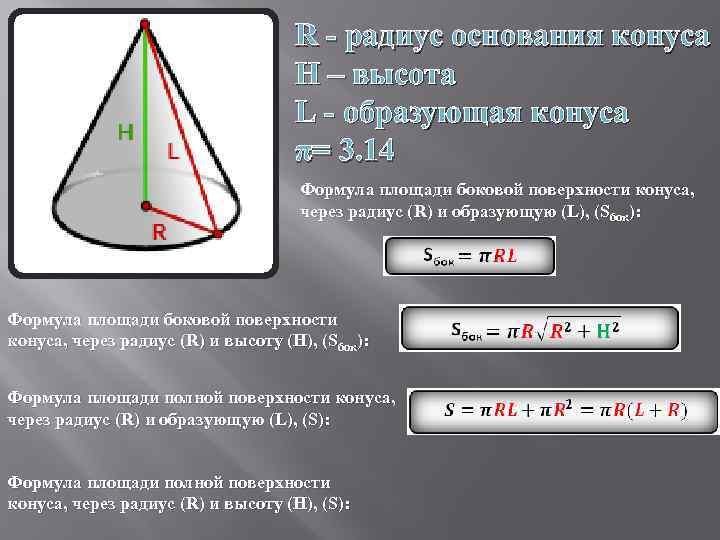 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S): Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S): Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
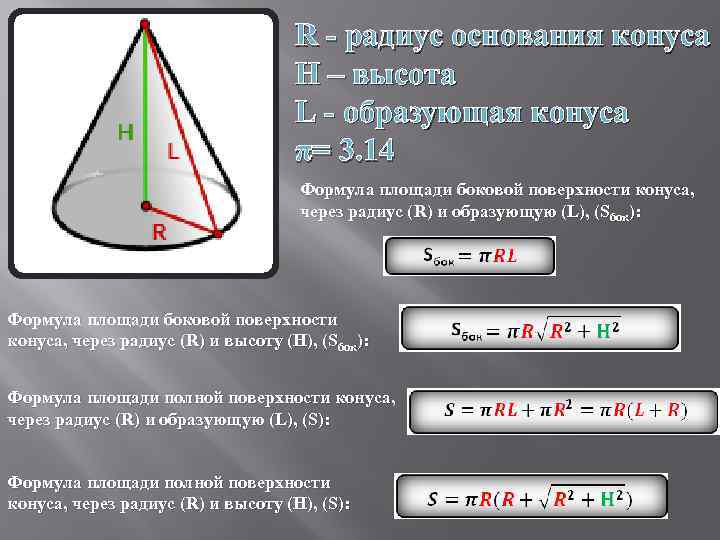 R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S): Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
R - радиус основания конуса H – высота L - образующая конуса π= 3. 14 Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок): Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок): Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S): Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
 Формулы площади поверхности усеченного конуса
Формулы площади поверхности усеченного конуса
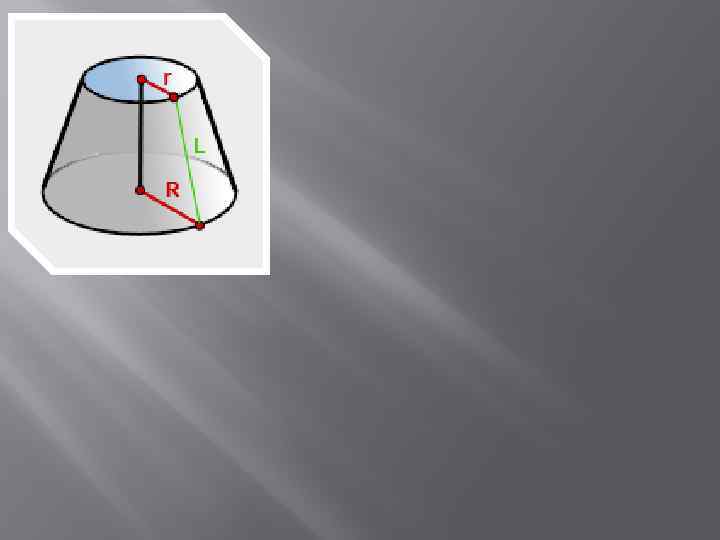
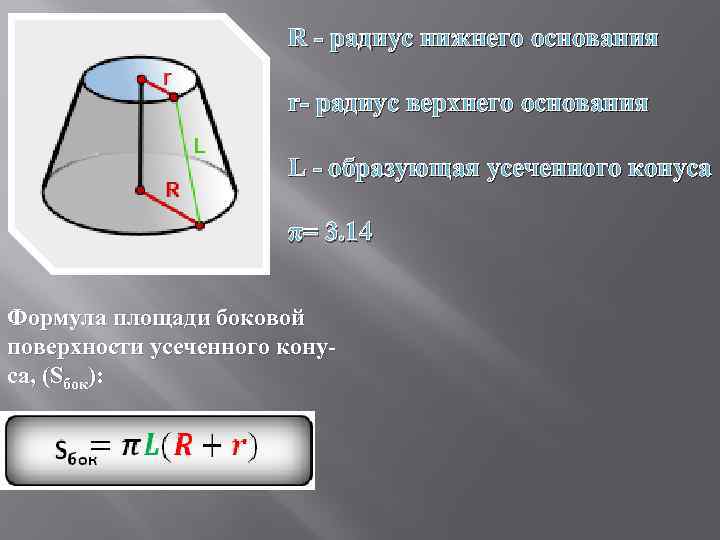
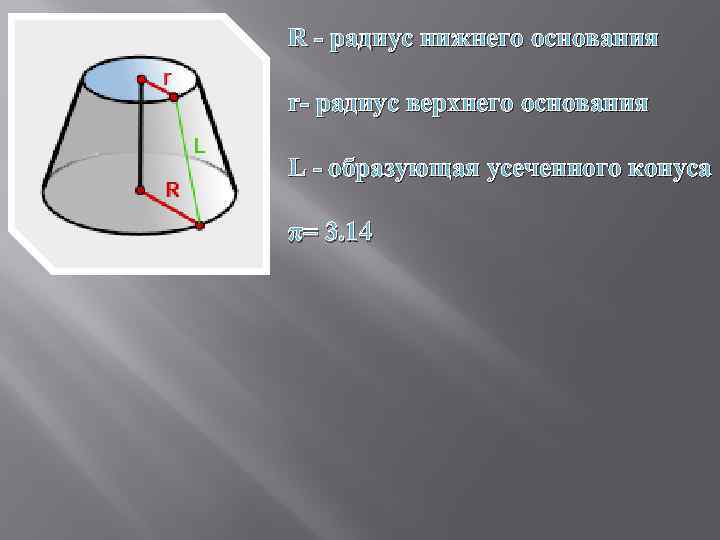 R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14
R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14
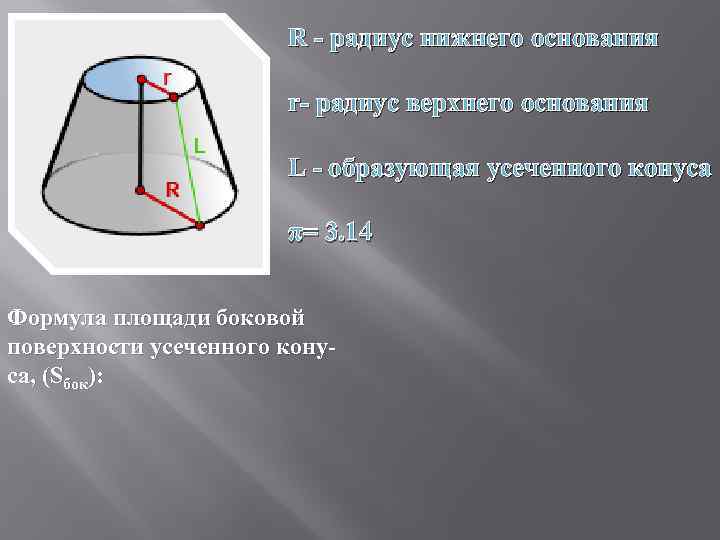 R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой поверхности усеченного конуса, (Sбок):
R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой поверхности усеченного конуса, (Sбок):
 R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой поверхности усеченного конуса, (Sбок):
R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой поверхности усеченного конуса, (Sбок):
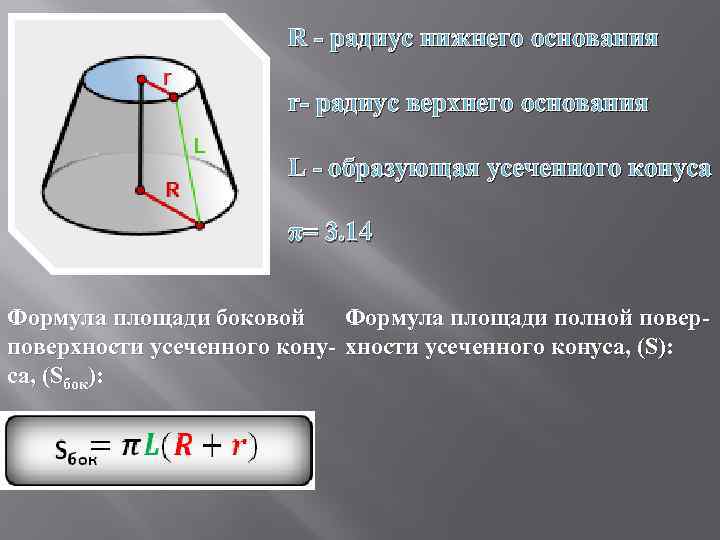 R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой Формула площади полной поверхности усеченного кону- хности усеченного конуса, (S): са, (Sбок):
R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой Формула площади полной поверхности усеченного кону- хности усеченного конуса, (S): са, (Sбок):
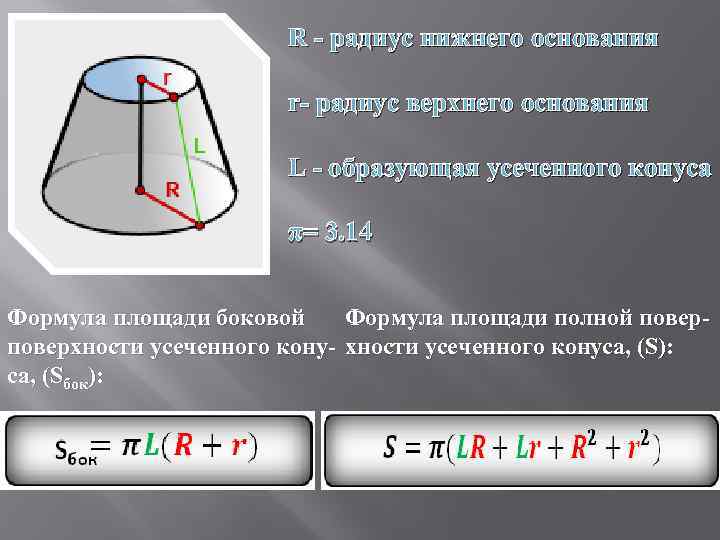 R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой Формула площади полной поверхности усеченного кону- хности усеченного конуса, (S): са, (Sбок):
R - радиус нижнего основания r- радиус верхнего основания L - образующая усеченного конуса π= 3. 14 Формула площади боковой Формула площади полной поверхности усеченного кону- хности усеченного конуса, (S): са, (Sбок):
 Tihonovich Natalia The End.
Tihonovich Natalia The End.


