2014_ЭМ_лекция_5.ppt
- Количество слайдов: 38
 Контрольный вопрос В плоский конденсатор, подключенный к аккумуляторной батарее, ввели диэлектрик, полностью заполняющий пространство между обкладками. Как изменилась энергия электрического поля внутри конденсатора? V = const C = 0 A/d U = C V 2/2 1
Контрольный вопрос В плоский конденсатор, подключенный к аккумуляторной батарее, ввели диэлектрик, полностью заполняющий пространство между обкладками. Как изменилась энергия электрического поля внутри конденсатора? V = const C = 0 A/d U = C V 2/2 1
 Cодержание сегодняшней лекции Ток и сопротивление Электрический ток. Микроскопическая модель тока. Сопротивление. Классическая модель электросопротивления. Электродвижущая сила (ЭДС). Правила Кирхгофа. Работа выхода электрона из металла. Контактная разность потенциалов. Термо. ЭДС. 2
Cодержание сегодняшней лекции Ток и сопротивление Электрический ток. Микроскопическая модель тока. Сопротивление. Классическая модель электросопротивления. Электродвижущая сила (ЭДС). Правила Кирхгофа. Работа выхода электрона из металла. Контактная разность потенциалов. Термо. ЭДС. 2
 Электрический ток 3
Электрический ток 3
 Электрический ток - суммарный заряд, переносимый в единицу времени через площадку, перпендикулярную вектору скорости перемещения носителей заряда. Аналогия между течением воды и электрическим током. Мгновенное значение тока Условность: ток течет в направлении перемещения положительных зарядов. Направление тока противоположно направлению перемещения отрицательных зарядов. 4
Электрический ток - суммарный заряд, переносимый в единицу времени через площадку, перпендикулярную вектору скорости перемещения носителей заряда. Аналогия между течением воды и электрическим током. Мгновенное значение тока Условность: ток течет в направлении перемещения положительных зарядов. Направление тока противоположно направлению перемещения отрицательных зарядов. 4
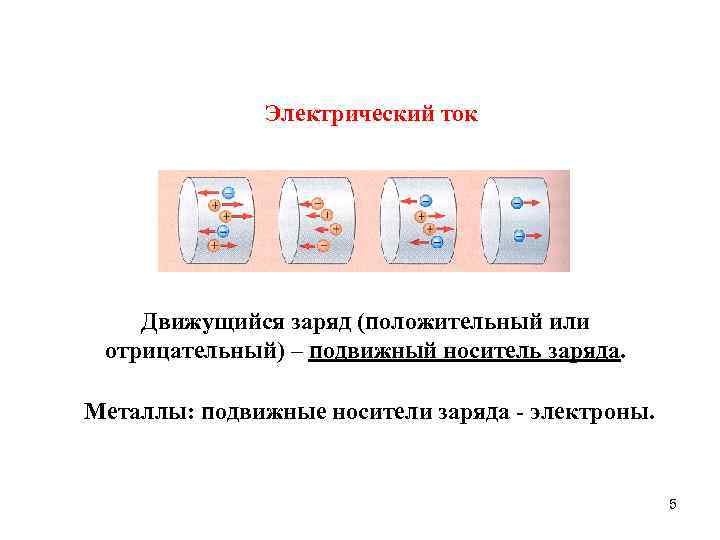 Электрический ток Движущийся заряд (положительный или отрицательный) – подвижный носитель заряда. Металлы: подвижные носители заряда - электроны. 5
Электрический ток Движущийся заряд (положительный или отрицательный) – подвижный носитель заряда. Металлы: подвижные носители заряда - электроны. 5
 Закон Ома в дифференциальной форме Джорд Симон Ом немецкий физик (1789 -1854) Для многих материалов (включая большинство металлов) величина , равная отношению плотности тока j к напряженности электрического поля E, есть величина постоянная, независящая от величины электрического поля, вызывающего ток. = j / E = const 6
Закон Ома в дифференциальной форме Джорд Симон Ом немецкий физик (1789 -1854) Для многих материалов (включая большинство металлов) величина , равная отношению плотности тока j к напряженности электрического поля E, есть величина постоянная, независящая от величины электрического поля, вызывающего ток. = j / E = const 6
 Закон Ома в интегральной форме Однородный проводник Закон Ома в интегральной форме - сопротивление проводника Ом ( ) - единица измерения сопротивления в СИ: Удельное электросопротивление [ ] – Ом метр ( м) 7
Закон Ома в интегральной форме Однородный проводник Закон Ома в интегральной форме - сопротивление проводника Ом ( ) - единица измерения сопротивления в СИ: Удельное электросопротивление [ ] – Ом метр ( м) 7
![Сопротивление Материал Удельное сопротивление (Ω м) Коэффициент теплового расширения [( C)-1] Cеребро 1, 59 Сопротивление Материал Удельное сопротивление (Ω м) Коэффициент теплового расширения [( C)-1] Cеребро 1, 59](https://present5.com/presentation/-57887135_287650852/image-8.jpg) Сопротивление Материал Удельное сопротивление (Ω м) Коэффициент теплового расширения [( C)-1] Cеребро 1, 59 10 -8 3, 8 10 -3 Медь 1, 7 10 -8 3, 9 10 -3 Золото 2, 44 10 -8 3, 4 10 -3 Алюминий 2, 82 10 -8 3, 9 10 -3 Вольфрам 5, 6 10 -8 4, 5 10 -3 Железо 10 10 -8 5, 0 10 -3 Платина 11 10 -8 3, 92 10 -3 Свинец 22 10 -8 3, 9 10 -3 Нихром 1, 50 10 -6 0, 4 10 -3 Углерод 3, 5 10 -5 -0, 5 10 -3 Германий 0, 46 -48 10 -3 Кремний 640 -75 10 -3 Стекло от 1010 до 1014 Эбонит 1013 Сера 1015 Кварц (плавленый) 75 1016 Все значения для 20 С 8
Сопротивление Материал Удельное сопротивление (Ω м) Коэффициент теплового расширения [( C)-1] Cеребро 1, 59 10 -8 3, 8 10 -3 Медь 1, 7 10 -8 3, 9 10 -3 Золото 2, 44 10 -8 3, 4 10 -3 Алюминий 2, 82 10 -8 3, 9 10 -3 Вольфрам 5, 6 10 -8 4, 5 10 -3 Железо 10 10 -8 5, 0 10 -3 Платина 11 10 -8 3, 92 10 -3 Свинец 22 10 -8 3, 9 10 -3 Нихром 1, 50 10 -6 0, 4 10 -3 Углерод 3, 5 10 -5 -0, 5 10 -3 Германий 0, 46 -48 10 -3 Кремний 640 -75 10 -3 Стекло от 1010 до 1014 Эбонит 1013 Сера 1015 Кварц (плавленый) 75 1016 Все значения для 20 С 8
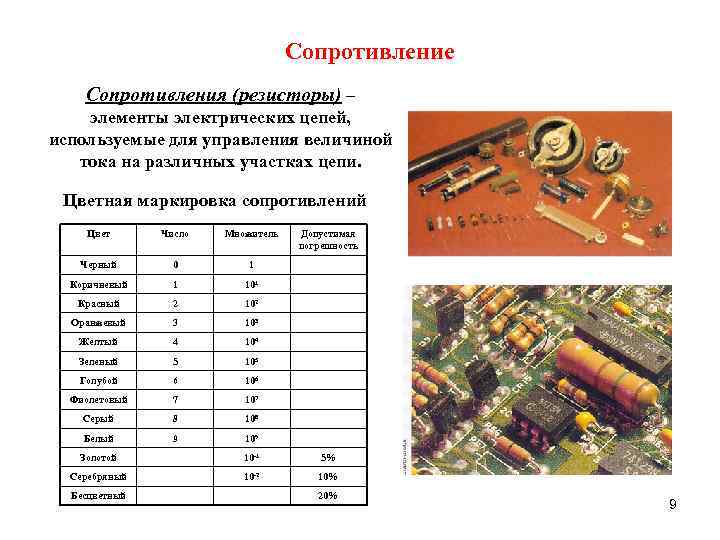 Сопротивление Сопротивления (резисторы) – элементы электрических цепей, используемые для управления величиной тока на различных участках цепи. Цветная маркировка сопротивлений Цвет Число Множитель Черный 0 1 Коричневый 1 101 Красный 2 102 Оранжевый 3 103 Желтый 4 104 Зеленый 5 105 Голубой 6 106 Фиолетовый 7 107 Серый 8 108 Белый 9 Допустимая погрешность 109 Золотой 10 -1 5% Серебряный 10 -2 10% Бесцветный 20% 9
Сопротивление Сопротивления (резисторы) – элементы электрических цепей, используемые для управления величиной тока на различных участках цепи. Цветная маркировка сопротивлений Цвет Число Множитель Черный 0 1 Коричневый 1 101 Красный 2 102 Оранжевый 3 103 Желтый 4 104 Зеленый 5 105 Голубой 6 106 Фиолетовый 7 107 Серый 8 108 Белый 9 Допустимая погрешность 109 Золотой 10 -1 5% Серебряный 10 -2 10% Бесцветный 20% 9
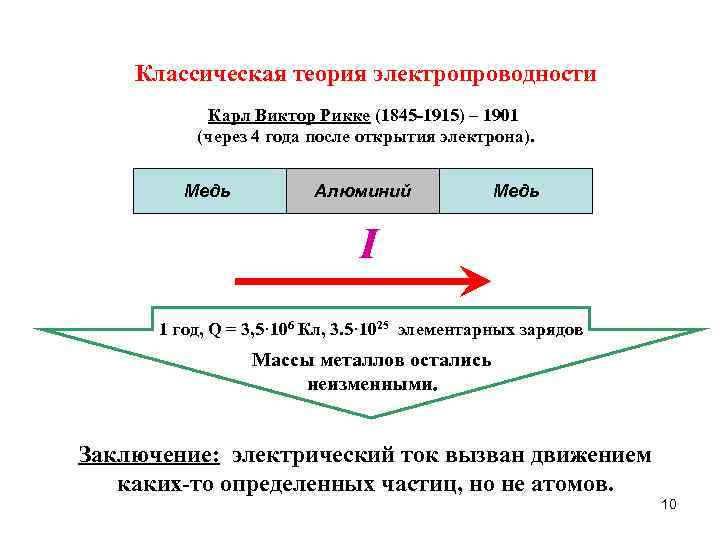 Классическая теория электропроводности Карл Виктор Рикке (1845 -1915) – 1901 (через 4 года после открытия электрона). Медь Алюминий Медь I 1 год, Q = 3, 5· 106 Кл, 3. 5· 1025 элементарных зарядов Массы металлов остались неизменными. Заключение: электрический ток вызван движением каких-то определенных частиц, но не атомов. 10
Классическая теория электропроводности Карл Виктор Рикке (1845 -1915) – 1901 (через 4 года после открытия электрона). Медь Алюминий Медь I 1 год, Q = 3, 5· 106 Кл, 3. 5· 1025 элементарных зарядов Массы металлов остались неизменными. Заключение: электрический ток вызван движением каких-то определенных частиц, но не атомов. 10
 Классическая модель электропроводности Идея Г. Лоренца: инерциальное движение зарядов после резкой остановки движущегося проводника должно вызвать электрический ток. Эксперимент Р. Толлмена и Т. Стюарта (1916): резкая остановка вращающейся с v = 300 м/с ( > 1000 км/час) катушки с проволокой (500 м) появление тока (движение отрицательных зарядов с удельным зарядом e/m, близким к характерному для электрона). Заключение: электрический ток вызван движением электронов. 11
Классическая модель электропроводности Идея Г. Лоренца: инерциальное движение зарядов после резкой остановки движущегося проводника должно вызвать электрический ток. Эксперимент Р. Толлмена и Т. Стюарта (1916): резкая остановка вращающейся с v = 300 м/с ( > 1000 км/час) катушки с проволокой (500 м) появление тока (движение отрицательных зарядов с удельным зарядом e/m, близким к характерному для электрона). Заключение: электрический ток вызван движением электронов. 11
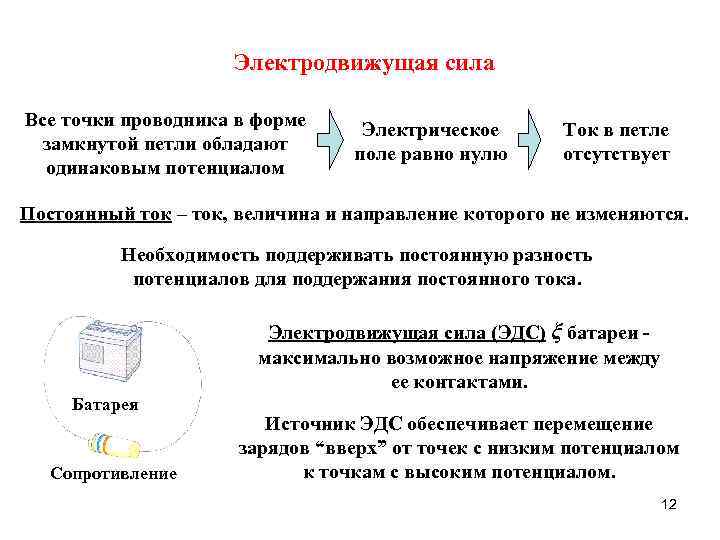 Электродвижущая сила Все точки проводника в форме замкнутой петли обладают одинаковым потенциалом Электрическое поле равно нулю Ток в петле отсутствует Постоянный ток – ток, величина и направление которого не изменяются. Необходимость поддерживать постоянную разность потенциалов для поддержания постоянного тока. Электродвижущая сила (ЭДС) ξ батареи максимально возможное напряжение между ее контактами. Батарея Сопротивление Источник ЭДС обеспечивает перемещение зарядов “вверх” от точек с низким потенциалом к точкам с высоким потенциалом. 12
Электродвижущая сила Все точки проводника в форме замкнутой петли обладают одинаковым потенциалом Электрическое поле равно нулю Ток в петле отсутствует Постоянный ток – ток, величина и направление которого не изменяются. Необходимость поддерживать постоянную разность потенциалов для поддержания постоянного тока. Электродвижущая сила (ЭДС) ξ батареи максимально возможное напряжение между ее контактами. Батарея Сопротивление Источник ЭДС обеспечивает перемещение зарядов “вверх” от точек с низким потенциалом к точкам с высоким потенциалом. 12
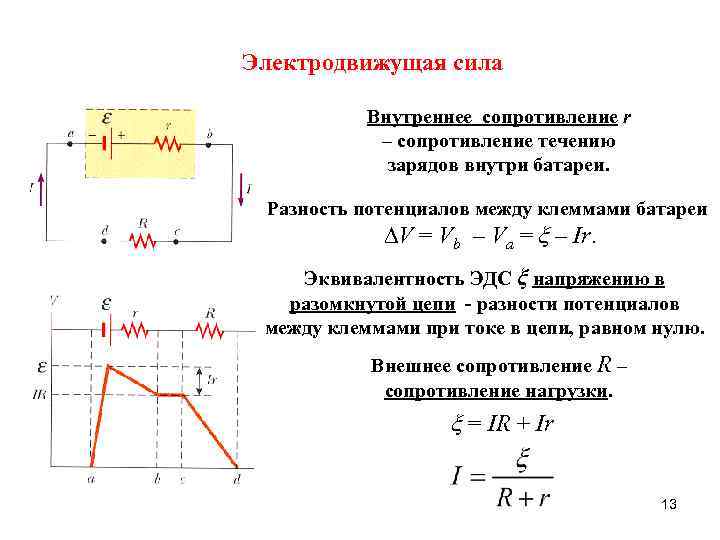 Электродвижущая сила Внутреннее сопротивление r – сопротивление течению зарядов внутри батареи. Разность потенциалов между клеммами батареи V = Vb – Va = ξ – Ir. Эквивалентность ЭДС ξ напряжению в разомкнутой цепи - разности потенциалов между клеммами при токе в цепи, равном нулю. Внешнее сопротивление R – сопротивление нагрузки. ξ = IR + Ir 13
Электродвижущая сила Внутреннее сопротивление r – сопротивление течению зарядов внутри батареи. Разность потенциалов между клеммами батареи V = Vb – Va = ξ – Ir. Эквивалентность ЭДС ξ напряжению в разомкнутой цепи - разности потенциалов между клеммами при токе в цепи, равном нулю. Внешнее сопротивление R – сопротивление нагрузки. ξ = IR + Ir 13
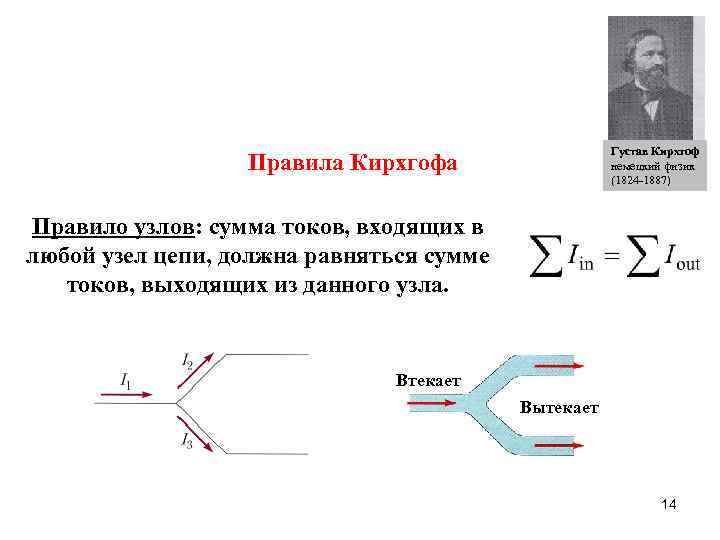 Густав Кирхгоф немецкий физик (1824 -1887) Правила Кирхгофа Правило узлов: cумма токов, входящих в любой узел цепи, должна равняться сумме токов, выходящих из данного узла. Втекает Вытекает 14
Густав Кирхгоф немецкий физик (1824 -1887) Правила Кирхгофа Правило узлов: cумма токов, входящих в любой узел цепи, должна равняться сумме токов, выходящих из данного узла. Втекает Вытекает 14
 Правила Кирхгофа Правило замкнутого контура: cумма разностей потенциалов вдоль всех элементов любого замкнутого контура должна равняться нулю. вдоль любого замкнутого контура 15
Правила Кирхгофа Правило замкнутого контура: cумма разностей потенциалов вдоль всех элементов любого замкнутого контура должна равняться нулю. вдоль любого замкнутого контура 15
 Классическая теория электропроводности металлов Суммарный заряд в объеме Mеталл n – концентрация носителей заряда в объеме, q – заряд носителя, A – площадь поперечного сечения, vd – скорость, t – интервал времени. Суммарный заряд, пересекающий со скоростью vd одно из оснований цилиндра за время t, равен Среднее значение тока в проводнике равно 16
Классическая теория электропроводности металлов Суммарный заряд в объеме Mеталл n – концентрация носителей заряда в объеме, q – заряд носителя, A – площадь поперечного сечения, vd – скорость, t – интервал времени. Суммарный заряд, пересекающий со скоростью vd одно из оснований цилиндра за время t, равен Среднее значение тока в проводнике равно 16
 Классическая теория электропроводности металлов vd – средняя скорость носителей заряда называется скоростью дрейфа. Если приложенная разность потенциалов V = 0, то свободные электроны движутся хаотично и vd = 0. Если V 0, свободные электроны раз за разом сталкиваются с атомами металла, их движение становится зигзагообразным и vd 0. Появление в проводнике эффективной внутренней силы трения в результате столкновения между движущимися электронами и ионами. Увеличение энергии колебаний ионов в результате этих столкновений и соответствующее увеличение температуры проводника. 17
Классическая теория электропроводности металлов vd – средняя скорость носителей заряда называется скоростью дрейфа. Если приложенная разность потенциалов V = 0, то свободные электроны движутся хаотично и vd = 0. Если V 0, свободные электроны раз за разом сталкиваются с атомами металла, их движение становится зигзагообразным и vd 0. Появление в проводнике эффективной внутренней силы трения в результате столкновения между движущимися электронами и ионами. Увеличение энергии колебаний ионов в результате этих столкновений и соответствующее увеличение температуры проводника. 17
 Сопротивление Заряды в проводнике в статическом равновесии, тогда Е=0 в проводнике. Вывод зарядов из равновесного состояния электрическим полем. Плотность тока Направление вектора плотности тока совпадает с направлением движения положительных зарядов Установление при поддержании определенной разности потенциалов между концами проводника определенной плотности тока j и напряженности электрического поля E. Некоторые (омические) материала: j = E, где коэффициент пропорциональности - электропроводность проводника. 18
Сопротивление Заряды в проводнике в статическом равновесии, тогда Е=0 в проводнике. Вывод зарядов из равновесного состояния электрическим полем. Плотность тока Направление вектора плотности тока совпадает с направлением движения положительных зарядов Установление при поддержании определенной разности потенциалов между концами проводника определенной плотности тока j и напряженности электрического поля E. Некоторые (омические) материала: j = E, где коэффициент пропорциональности - электропроводность проводника. 18
 Классическая электронная теория Закон Ома Предположение: пусть в металлическом проводнике существует Ускорение а заряда е под действием силы F Cкорость электрона к концу свободного пробега 19
Классическая электронная теория Закон Ома Предположение: пусть в металлическом проводнике существует Ускорение а заряда е под действием силы F Cкорость электрона к концу свободного пробега 19
 Классическая электронная теория Закон Ома Классическая теория металлов Друде: передача накопленной электроном энергии иону в конце свободного пробега. Следствие: средняя скорость направленного движения электрона Друде: распределение электронов по скоростям не учитывается. Зависимость среднего времени
Классическая электронная теория Закон Ома Классическая теория металлов Друде: передача накопленной электроном энергии иону в конце свободного пробега. Следствие: средняя скорость направленного движения электрона Друде: распределение электронов по скоростям не учитывается. Зависимость среднего времени
 Классическая электронная теория Закон Ома < v > << < u >
Классическая электронная теория Закон Ома < v > << < u >
 Классическая электронная теория Закон Ома в дифференциальной форме Удельная проводимость металла электронов концентрации свободных n и средней длине свободного пробега < l >. 22
Классическая электронная теория Закон Ома в дифференциальной форме Удельная проводимость металла электронов концентрации свободных n и средней длине свободного пробега < l >. 22
 Классическая электронная теория Закон Джоуля-Ленца Дополнительная кинетическая энергия, приобретенная электроном к концу свободного пробега под действием поля, Передача < Ek > решетке и повышение ее энергии (нагревание) при соударении электрона с ионом. < z > = < u > / < l > - cреднее число столкновений электрона с узлами решетки за единицу времени. Передача энергии w = n < z > < Eк > за n < z > cтолкновений, где n – концентрация электронов. 23
Классическая электронная теория Закон Джоуля-Ленца Дополнительная кинетическая энергия, приобретенная электроном к концу свободного пробега под действием поля, Передача < Ek > решетке и повышение ее энергии (нагревание) при соударении электрона с ионом. < z > = < u > / < l > - cреднее число столкновений электрона с узлами решетки за единицу времени. Передача энергии w = n < z > < Eк > за n < z > cтолкновений, где n – концентрация электронов. 23
 Классическая электронная теория Закон Джоуля-Ленца Энергия, передаваемая единице объема проводника в единицу времени и идущая на нагревание проводника, Равенство коэффициента пропорциональности между удельной тепловой мощностью тока w и E 2 удельной электропроводности . Закон Джоуля-Ленца в дифференциальной форме 24
Классическая электронная теория Закон Джоуля-Ленца Энергия, передаваемая единице объема проводника в единицу времени и идущая на нагревание проводника, Равенство коэффициента пропорциональности между удельной тепловой мощностью тока w и E 2 удельной электропроводности . Закон Джоуля-Ленца в дифференциальной форме 24
 Классическая электронная теория Закон Видемана-Франца Большая электропроводность и высокая теплопроводность металлов. Причина: носители тока и теплоты – одни и те же частицы (свободные электроны). Перенос свободными электронами при перемещении в металле не только электрического заряда, но и присущей им энергии хаотического (теплового) движения, т. е. теплоты. 25
Классическая электронная теория Закон Видемана-Франца Большая электропроводность и высокая теплопроводность металлов. Причина: носители тока и теплоты – одни и те же частицы (свободные электроны). Перенос свободными электронами при перемещении в металле не только электрического заряда, но и присущей им энергии хаотического (теплового) движения, т. е. теплоты. 25
 Классическая электронная теория Закон Видемана-Франца Экспериментальный закон Видемана и Франца (1853 г. ): отношение теплопроводности к удельной проводимости для всех металлов и при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре / = T, - постоянная, не зависящая от рода металла. 26
Классическая электронная теория Закон Видемана-Франца Экспериментальный закон Видемана и Франца (1853 г. ): отношение теплопроводности к удельной проводимости для всех металлов и при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре / = T, - постоянная, не зависящая от рода металла. 26
 Классическая электронная теория Закон Видемана-Франца Элементарная классическая теория электропроводности металлов предсказывает = 3 (к/e)2, где к – постоянная Больцмана. Хорошее согласие теории с экспериментом. 27
Классическая электронная теория Закон Видемана-Франца Элементарная классическая теория электропроводности металлов предсказывает = 3 (к/e)2, где к – постоянная Больцмана. Хорошее согласие теории с экспериментом. 27
 Классическая электронная теория Недостатки Температурная зависимость сопротивления Удельное сопротивление Теория: n и < l > от T не зависят Эксперимент: 28
Классическая электронная теория Недостатки Температурная зависимость сопротивления Удельное сопротивление Теория: n и < l > от T не зависят Эксперимент: 28
 Классическая электронная теория Недостатки Оценка длины свободного пробега электронов в металлах Удельное сопротивление Теория: Завышенные значения длины свободного пробега электронов (прохождение электроном сотен межузельных расстояний без соударения с ионами кристаллической решетки) для совпадения с экспериментом. 29
Классическая электронная теория Недостатки Оценка длины свободного пробега электронов в металлах Удельное сопротивление Теория: Завышенные значения длины свободного пробега электронов (прохождение электроном сотен межузельных расстояний без соударения с ионами кристаллической решетки) для совпадения с экспериментом. 29
 Классическая электронная теория Недостатки Теплоемкость металлов Вклад кристаллической решетки и электронного газа. Атомная (рассчитанная на 1 моль) теплоемкость у металлов выше, чем у диэлектриков, у которых нет свободных электронов. Закон Дюлонга и Пти: теплоемкость одноатомного кристалла равна 3 R. Теплоемкость одноатомного электронного газа равна 3/2 R. Атомная теплоемкость металлов должна быть равна 4, 5 R. 30
Классическая электронная теория Недостатки Теплоемкость металлов Вклад кристаллической решетки и электронного газа. Атомная (рассчитанная на 1 моль) теплоемкость у металлов выше, чем у диэлектриков, у которых нет свободных электронов. Закон Дюлонга и Пти: теплоемкость одноатомного кристалла равна 3 R. Теплоемкость одноатомного электронного газа равна 3/2 R. Атомная теплоемкость металлов должна быть равна 4, 5 R. 30
 Классическая электронная теория Недостатки Теплоемкость металлов Эксперимент: атомная теплоемкость равна 3 R как у металлов, так и у диэлектриков. Классическая электронная теория: невозможность объяснить почему наличие электронов проводимости практически не сказывается на значении теплоемкости. 31
Классическая электронная теория Недостатки Теплоемкость металлов Эксперимент: атомная теплоемкость равна 3 R как у металлов, так и у диэлектриков. Классическая электронная теория: невозможность объяснить почему наличие электронов проводимости практически не сказывается на значении теплоемкости. 31
 / = T Классическая электронная теория Недостатки Закон Видемана - Франца Хорошее согласие теории с экспериментом - случайность. Расчеты Лоренца с учетом применения к электронному газу статистики Максвелла-Больцмана: = 2 (к / е)2. Резкое расхождение теории с экспериментом. 32
/ = T Классическая электронная теория Недостатки Закон Видемана - Франца Хорошее согласие теории с экспериментом - случайность. Расчеты Лоренца с учетом применения к электронному газу статистики Максвелла-Больцмана: = 2 (к / е)2. Резкое расхождение теории с экспериментом. 32
 Классическая электронная теория Объяснение расхождений классической электронной теории металлов с экспериментом – поведение электронов проводимости надо описывать не статистикой Максвелла-Больцмана, а квантовой статистикой. Правильные качественные предсказания классической электронной теории во многих случаях, например, при малой концентрации электронов проводимости и высокой температуре. Простота и наглядность классической электронной теории. 33
Классическая электронная теория Объяснение расхождений классической электронной теории металлов с экспериментом – поведение электронов проводимости надо описывать не статистикой Максвелла-Больцмана, а квантовой статистикой. Правильные качественные предсказания классической электронной теории во многих случаях, например, при малой концентрации электронов проводимости и высокой температуре. Простота и наглядность классической электронной теории. 33
 Работа выхода электронов из металла Отрицательное облако из электронов _ _ _ _ + + + + Положительно заряженный металл Две причины, способствующие тому, чтобы свободные электроны не покидали металл: - электростатическое притяжение между положительно заряженным металлом и отрицательно заряженным электроном; - потенциальный барьер между положительно заряженным металлом и облаком отрицательно заряженных электронов (“заряженный конденсатор”) с разностью потенциалов ΔV. 34
Работа выхода электронов из металла Отрицательное облако из электронов _ _ _ _ + + + + Положительно заряженный металл Две причины, способствующие тому, чтобы свободные электроны не покидали металл: - электростатическое притяжение между положительно заряженным металлом и отрицательно заряженным электроном; - потенциальный барьер между положительно заряженным металлом и облаком отрицательно заряженных электронов (“заряженный конденсатор”) с разностью потенциалов ΔV. 34
 Работа выхода электронов из металла Возможность покидания электроном поверхности металла, если кинетическая энергия электрона - работа выхода электрона из металла [W] = э. В. T 300 K: Ek= 0, 026 э. В, но W несколько э. В. Вывод: лишь небольшое количество электронов может покинуть металл при комнатной температуре. 35
Работа выхода электронов из металла Возможность покидания электроном поверхности металла, если кинетическая энергия электрона - работа выхода электрона из металла [W] = э. В. T 300 K: Ek= 0, 026 э. В, но W несколько э. В. Вывод: лишь небольшое количество электронов может покинуть металл при комнатной температуре. 35
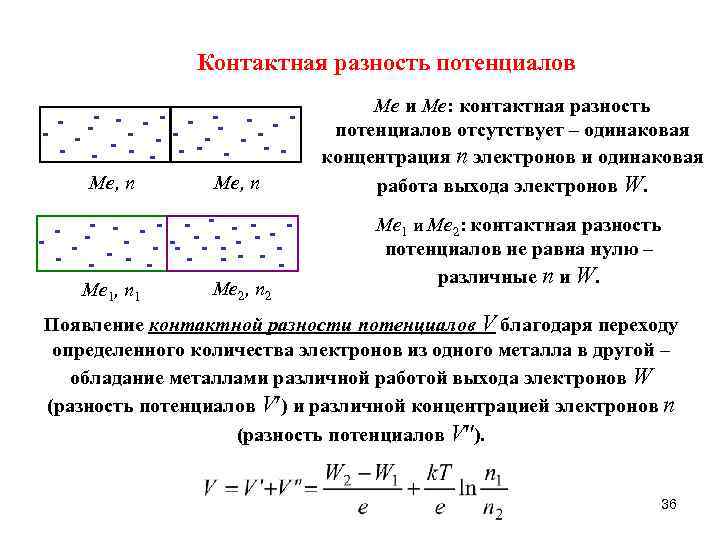 Контактная разность потенциалов - -- - - -- - - Me, n - -- - - -- - - Me 2, n 2 Me 1, n 1 Me и Me: контактная разность потенциалов отсутствует – одинаковая концентрация n электронов и одинаковая работа выхода электронов W. Me 1 и Me 2: контактная разность потенциалов не равна нулю – различные n и W. Появление контактной разности потенциалов V благодаря переходу определенного количества электронов из одного металла в другой – обладание металлами различной работой выхода электронов W (разность потенциалов V ) и различной концентрацией электронов n (разность потенциалов V ). 36
Контактная разность потенциалов - -- - - -- - - Me, n - -- - - -- - - Me 2, n 2 Me 1, n 1 Me и Me: контактная разность потенциалов отсутствует – одинаковая концентрация n электронов и одинаковая работа выхода электронов W. Me 1 и Me 2: контактная разность потенциалов не равна нулю – различные n и W. Появление контактной разности потенциалов V благодаря переходу определенного количества электронов из одного металла в другой – обладание металлами различной работой выхода электронов W (разность потенциалов V ) и различной концентрацией электронов n (разность потенциалов V ). 36
 Термо. ЭДС Два металла A и B, два контакта 1 и 2. A V 1 и V 2 – контактные разности потенциалов. T 1 T 2 B Различные знаки термо. ЭДС ξ 1 и ξ 2 в контактах. T 1 = T 2: V 1 = V 2, ΣVi = 0, I = 0. T 1 ≠ T 2: V 1 ≠ V 2, ΣVi ≠ 0, I 0. 37
Термо. ЭДС Два металла A и B, два контакта 1 и 2. A V 1 и V 2 – контактные разности потенциалов. T 1 T 2 B Различные знаки термо. ЭДС ξ 1 и ξ 2 в контактах. T 1 = T 2: V 1 = V 2, ΣVi = 0, I = 0. T 1 ≠ T 2: V 1 ≠ V 2, ΣVi ≠ 0, I 0. 37
 Контрольный вопрос Предположим, что металлическая проволока имеет постепенно уменьшающуюся вдоль ее длины площадь поперечного сечения. Какой из приведенных ниже ответов справедлив: (a) скорость дрейфа носителей заряда и сопротивление возрастают; (б) скорость дрейфа носителей заряда и сопротивление убывают; (в) скорость дрейфа увеличивается, а сопротивление убывает; (г) скорость дрейфа уменьшается, а сопротивление увеличивается вдоль длины проволоки. 38
Контрольный вопрос Предположим, что металлическая проволока имеет постепенно уменьшающуюся вдоль ее длины площадь поперечного сечения. Какой из приведенных ниже ответов справедлив: (a) скорость дрейфа носителей заряда и сопротивление возрастают; (б) скорость дрейфа носителей заряда и сопротивление убывают; (в) скорость дрейфа увеличивается, а сопротивление убывает; (г) скорость дрейфа уменьшается, а сопротивление увеличивается вдоль длины проволоки. 38


