Континуальный критерий Va R CC-Va R на финансовых

Скачать презентацию Континуальный критерий Va R CC-Va R на финансовых

c945e4e14e128908196fb53af0ffa126.ppt

Количество слайдов: 141

Континуальный критерий Va. R (CC-Va. R) на финансовых рынках Часть II Агасандян Г. А. Вычислительный центр РАН

Многомерные рынки • Рассматривается однопериодный финансовый рынок с n базовыми активами, значения которых образуют вектор x X n. • Инвестор характеризуется неотрицательной, монотонно возрастающей и непрерывной функцией рисковых предпочтений (ф. р. п. ) ( ), [0, 1], определяющей его склонность к риску. Пример: ( )= , [0, 1], >0, при этом большие значения параметра отвечают большей готовности инвестора идти на риск ради увеличения средней доходности. • Континуальный критерий Va. R (CC-Va. R) требует, чтобы при заданной инвестиционной сумме S случайный доход q, порожденный строящимся из имеющихся на рынке инструментов (оптимальным) портфелем, удовлетворял неравенствам P{q ( )} 1– для всех [0, 1], где P{M} – вероятность множества M (распределение вероятности составляет прогноз инвестора).

Многомерные рынки Предполагается, что многомерный однопериодный рынок образован несколькими (n>1) базовыми активами. На нем обращаются также инструменты, платежные функции которых определяются в общем случае совокупностью цен всех базовых активов. Рассматривается многомерный -рынок на основе многомерных -инструментов, а также рынок опционов, на котором особую роль играют элементарные инструменты, называемые -опционами. Вводятся x = (x 1, x 2, …, xn), ς = (ς1, ς2, …, ςn) и α = (α 1, α 2, …, αn) – векторы соответственно цен базовых активов xi , страйков ςi , i N={1, …, n}, и чисел αi {– 1, 1}, характеризующих тип опциона. Тогда α-опцион A(ς; α), по которому доход выплачивается в конечный момент времени, определяется платежной функцией max(0, α 1(x 1–ς1)). . . max(0, αn(xn–ςn)). Размерность доходов и цен опционов одинакова, но может не быть связана с размерностями базовых активов. Как и в одномерном случае, благодаря теоремам паритета опционов присутствие на рынке всех 2 n α-опционов для каждого ς n не является обязательным.

Многомерный -рынок

Многомерный рынок опционов

Многомерный рынок ζ-опционов

Многомерный рынок опционов

Двумерный рынок опционов

Многомерный рынок опционов

Двумерный рынок опционов

Двумерный рынок опционов Двумерный базисный внутренний баттерфляй B[2, 2]

Двумерный рынок опционов Двумерный базисный вершинный спред B[1, k 2]

Двумерный рынок опционов Двумерный базисный реберный баттерспред B[2, k 2]

Двумерный рынок опционов

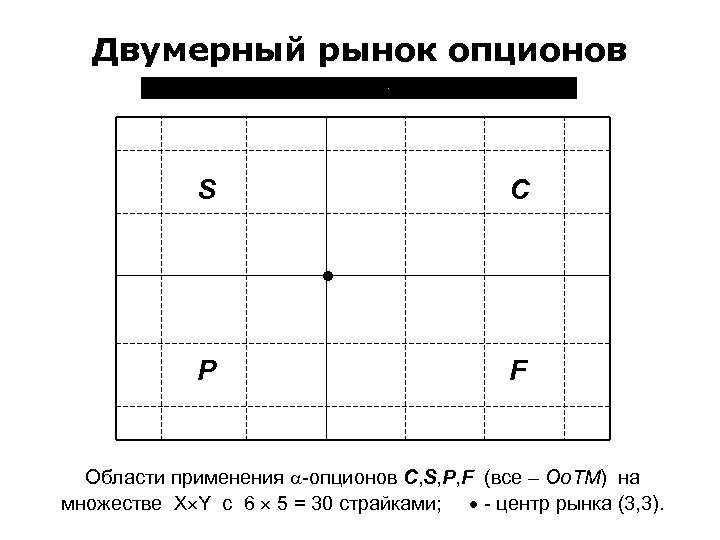Двумерный рынок опционов S C P F Области применения -опционов C, S, P, F (все – Oo. TM) на множестве X Y с 6 5 = 30 страйками; - центр рынка (3, 3).

Двумерный рынок опционов

Двумерный рынок опционов Пример. Подготовка данных X=Y=[-1, 1]; p(x, y) = 13/36 - x 2/6 - y 2/6 (график слева); c(x, y) = 37/120 - (x+1/2)2/20 - (y-1/2)2/20 (график справа); |C(s, t)| = (1 -s)2(1 -t)2(28 -4 s-s 2 -t 2)/480; x, s X; y, t Y; |S(s, t)| = (1+s)2(1 -t)2(36 -s 2 -t 2)/480; |P(s, t)| = (1+s)2(1+t)2(28 -s 2+4 t-t 2)/480; |F(s, t)| = (1 -s)2(1+t)2(20 -4 s-s 2+4 t-t 2)/480; |CX(s)| = (1 -s)2(25 -4 s-s 2)/120; |CY(t)| = (1 -t)2(33 -t 2)/120; |PY(s)| = (1+s)2(33 -s 2)/120; |PY(t)| = (1+t)2(25+4 t-t 2)/120.

Двумерный рынок опционов Пример. Базисные баттерфляи B C B[1, 1]=U+(CX[2]-CX[1])/h 1+(CY[2]-CY[1])/h 2+(C[2, 2]-C[1, 2]C[2, 1]+C[1, 1])/h 1/h 2; B[1, k 2]=(CY[k 2 -1]-CY[k 2])/h 2+(C[1, k 2]-C[2, k 2]-C[1, k 2 -1]+C[2, k 2 -1]) /h 1/h 2; B[k 1, 1]=(CX[k 1 -1]-CX[k 1])/h 1+(C[k 1, 1]-C[k 1, 2]-C[k 1 -1, 1]+C[k 1 -1, 2]) /h 1/h 2; B[k 1, k 2]=(C[k 1, k 2]-C[k 1, k 2 -1]-C[k 1 -1, k 2]+C[k 1 -1, k 2 -1])/h 1/h 2; B[1, j]=(CY[j-1]-2 CY[j]+CY[j+1])/h 2+(C[2, j-1]-2 C[2, j]+C[2, j+1]-C[1, j -1]+2 C[1, j]-C[1, j+1])/h 1/h 2, j=2, …, k 2 -1; B[k 1, j]=(C[k 1 -1, j-1]-2 C[k 1 -1, j]+C[k 1 -1, j+1]-C[k 1, j-1]+2 C[k 1, j]C[k 1, j+1])/h 1/h 2, j=2, …, k 2 -1; B[i, 1]=(CX[i-1]-2 CX[i]+CX[i+1])/h 1+(C[i-1, 2]-2 C[i, 2]+C[i+1, 2]C[i-1, 1]+2 C[i, 1]-C[i+1, 1])/h 1/h 2, i=2, …, k 1 -1; B[i, k 2]=(C[i-1, k 2 -1]-2 C[i, k 2 -1]+C[i+1, k 2 -1]-C[i-1, k 2]+2 C[i, k 2]C[i+1, k 2])/h 1/h 2, i=2, …, k 1 -1; B[i, j]=(4 C[i, j]-2 C[i+1, j]-2 C[i-1, j]-2 C[i, j+1]-2 C[i, j-1]+C[i+1, j+1]+ C[i+1, j-1]+C[i-1, j+1]+C[i-1, j-1])/h 1/h 2, i=2, …, k 1 -1, j=2, …, k 2 -1;

Двумерный рынок опционов Пример. Базисные баттерфляи B F B[1, 1]=(FY[2]-FY[1])/h 2+(F[2, 2]-F[1, 2]-F[2, 1]+F[1, 1])/h 1/h 2; B[1, k 2]=U+(FX[2]-FX[1])/h 1+(FY[k 2 -1]-FY[k 2])/h 2+(F[1, k 2]-F[2, k 2]F[1, k 2 -1]+F[2, k 2 -1]) /h 1/h 2; B[k 1, 1]=(F[k 1, 1]-F[k 1, 2]-F[k 1 -1, 1]+F[k 1 -1, 2]) /h 1/h 2; B[k 1, k 2]=(FX[k 1 -1]-FX[k 1])/h 1+(F[k 1, k 2]-F[k 1, k 2 -1]-F[k 1 -1, k 2]+F[k 1 -1, k 2 -1])/h 1/h 2; B[1, j]=(FY[j-1]-2 FY[j]+FY[j+1])/h 2+(F[2, j-1]-2 F[2, j]+F[2, j+1]- F[1, j 1]+2 F[1, j]-F[1, j+1])/h 1/h 2, j=2, …, k 2 -1; B[k 1, j]=(F[k 1 -1, j-1]-2 F[k 1 -1, j]+F[k 1 -1, j+1]-F[k 1, j-1]+2 F[k 1, j]F[k 1, j+1])/h 1/h 2, j=2, …, k 2 -1; B[i, 1]=(F[i-1, 2]-2 F[i, 2]+F[i+1, 2]-F[i-1, 1]+2 F[i, 1]-F[i+1, 1])/h 1/h 2, i=2, …, k 1 -1; B[i, k 2]=(FX[i-1]-2 FX[i]+FX[i+1])/h 1+(F[i-1, k 2 -1]-2 F[i, k 2 -1]+F[i+1, k 21]-F[i-1, k 2]+2 F[i, k 2]-F[i+1, k 2])/h 1/h 2, i=2, …, k 1 -1; B[i, j]=(4 F[i, j]-2 F[i+1, j]-2 F[i-1, j]-2 F[i, j+1]-2 F[i, j-1]+F[i+1, j+1]+ F[i+1, j-1]+F[i-1, j+1]+F[i-1, j-1])/h 1/h 2, i=2, …, k 1 -1, j=2, …, k 2 -1;

Двумерный рынок опционов Пример. Базисные смешанные баттерфляи B C, S, P, F Вершинные баттерфляи: B[1, 1]=(P[1, 1]-P[1, 2]-P[2, 1]+P[2, 2])/h 1/h 2; B[1, k 2]=(S[1, k 2]-S[2, k 2]-S[1, k 2 -1]+S[2, k 2 -1])/h 1/h 2; B[k 1, 1]=(F[k 1, 1]-F[k 1, 2]-F[k 1 -1, 1]+F[k 1 -1, 2])/h 1/h 2; B[k 1, k 2]=(C[k 1, k 2]-C[k 1, k 2 -1]-C[k 1 -1, k 2]+C[k 1 -1, k 2 -1])/h 1/h 2; Смешанные реберные баттерфляи: B[ic, k 2]=(CY[k 2 -1]-CY[k 2])/h 2 -(C[ic, k 2 -1]-C[ic, k 2]-C[ic+1, k 2 -1]+ C[ic+1, k 2] +S[ic, k 2 -1]-S[ic, k 2]-S[ic-1, k 2 -1]+S[ic-1, k 2])/h 1/h 2; B[1, jc]=(PX[2]-PX[1])/h 1 -(S[1, jc+1]-S[1, jc]-S[2, jc+1]+S[2, jc]+ P[1, jc -1]-P[1, jc]-P[2, jc-1]+P[2, jc])/h 1/h 2; B[ic, 1]=(PY[2]-PY[1])/h 2 -(P[ic, 2]-P[ic, 1]-P[ic-1, 2]+P[ic-1, 1]+F[ic, 2]F[ic, 1]-F[ic+1, 2]+F[ic+1, 1])/h 1/h 2; B[k 1, jc]=(CX[k 1 -1]-CX[k 1])/h 1 -(C[k 1, jc+1]-C[k 1, jc]-C[k 1 -1, jc+1]+ C[k 1 -1, jc]+F[k 1, jc-1]-F[k 1, jc]-F[k 1 -1, jc-1]+F[k 1 -1, jc])/h 1/h 2;

Двумерный рынок опционов Пример. Базисные смешанные баттерфляи B C, S, P, F Простые реберные баттерфляи: B[k 1, j]=(C[k 1 -1, j-1]-2 C[k 1 -1, j]+C[k 1 -1, j+1]-C[k 1, j-1]+2 C[k 1, j]C[k 1, j+1]) /h 1/h 2, j=jc+1, . . , k 2 -1; B[i, k 2]=(C[i-1, k 2 -1]-2 C[i, k 2 -1]+C[i+1, k 2 -1]-C[i-1, k 2]+2 C[i, k 2]C[i+1, k 2]) /h 1/h 2, i=ic+1, …, k 1 -1; B[1, j]=(S[2, j-1]-2 S[2, j]+S[2, j+1]-S[1, j-1]+2 S[1, j]-S[1, j+1])/h 1/h 2, j=jc+1, . . , k 2 -1; B[i, k 2]=(S[i-1, k 2 -1]-2 S[i, k 2 -1]+S[i+1, k 2 -1]-S[i-1, k 2]+2 S[i, k 2]S[i+1, k 2]) /h 1/h 2, i=2, …, ic-1; B[1, j]=(P[2, j-1]-2 P[2, j]+P[2, j+1]-P[1, j-1]+2 P[1, j]-P[1, j+1])/h 1/h 2, j=2, …, jc-1; B[i, 1]=(P[i-1, 2]-2 P[i, 2]+P[i+1, 2]-P[i-1, 1]+2 P[i, 1]-P[i+1, 1])/h 1/h 2, i=2, . . , ic-1; B[i, 1]=(F[i-1, 2]-2 F[i, 2]+F[i+1, 2]-F[i-1, 1]+2 F[i, 1]-F[i+1, 1])/h 1/h 2, i=ic+1, . . , k 1 -1; B[k 1, j]=(F[k 1 -1, j-1]-2 F[k 1 -1, j]+F[k 1 -1, j+1]-F[k 1, j-1]+2 F[k 1, j]F[k 1, j+1])/h 1/h 2, j=2, . . , jc-1;

Двумерный рынок опционов Пример. Базисные смешанные баттерфляи B C, S, P, F Смешанные осевые баттерфляи: B[ic, j]=(CY[j-1]-2 CY[j]+CY[j+1])/h 2 -(C[ic, j-1]-2 C[ic, j]+C[ic, j+1]C[ic+1, j-1]+2 C[ic+1, j]-C[ic+1, j+1]+S[ic, j-1]-2 S[ic, j]+S[ic, j+1]S[ic-1, j-1]+2 S[ic-1, j]-S[ic-1, j+1])/h 1/h 2, j=jc+1, …, k 2 -1; B[i, jc]=(PX[i-1]-2 PX[i]+PX[i+1])/h 1 -(S[i-1, jc]-2 S[i, jc]+S[i+1, jc]S[i-1, jc+1]+2 S[i, jc+1]-S[i+1, jc+1]+P[i-1, jc]-2 P[i, jc]+P[i+1, jc]P[i-1, jc-1]+2 P[i, jc-1]-P[i+1, jc-1])/h 1/h 2, i=2, …, ic-1; B[ic, j]=(PY[j-1]-2 PY[j]+PY[j+1])/h 2 -(P[ic, j-1]-2 P[ic, j]+P[ic, j+1]P[ic-1, j-1]+2 P[ic-1, j]-P[ic-1, j+1]+F[ic, j-1]-2 F[ic, j]+F[ic, j+1]F[ic+1, j-1]+2 F[ic+1, j]-F[ic+1, j+1])/h 1/h 2, j=2, …, jc-1; B[i, jc]=(CX[i-1]-2 CX[i]+CX[i+1])/h 1 -(C[i-1, jc]-2 C[i, jc]+C[i+1, jc]C[i-1, jc+1]+2 C[i, jc+1]-C[i+1, jc+1]+F[i-1, jc]-2 F[i, jc]+F[i+1, jc]F[i-1, jc-1]+2 F[i, jc-1]-F[i+1, jc-1])/h 1/h 2, i=ic+1, …, k 1 -1.

Двумерный рынок опционов Пример. Базисные смешанные баттерфляи B C, S, P, F Внутренние баттерфляи: B[i, j]=(4 C[i, j]-2 C[i+1, j]-2 C[i-1, j]-2 C[i, j+1]-2 C[i, j-1]+C[i+1, j+1] +C[i+1, j-1]+C[i-1, j+1]+C[i-1, j-1])/h 1/h 2, i=ic+1, …, k 1 -1, j=jc+1, k 2 -1; B[i, j]=(4 S[i, j]-2 S[i+1, j]-2 S[i-1, j]-2 S[i, j+1]-2 S[i, j-1]+S[i+1, j+1]+ S[i+1, j-1]+S[i-1, j+1]+S[i-1, j-1])/h 1/h 2, i=2, ic-1, j=jc+1, …, k 2 -1; B[i, j]=(4 P[i, j]-2 P[i+1, j]-2 P[i-1, j]-2 P[i, j+1]-2 P[i, j-1]+P[i+1, j+1]+ P[i+1, j-1]+P[i-1, j+1]+P[i-1, j-1])/h 1/h 2, i=2, …, ic-1, j=2, …, jc-1; B[i, j]=(4 F[i, j]-2 F[i+1, j]-2 F[i-1, j]-2 F[i, j+1]-2 F[i, j-1]+F[i+1, j+1]+ F[i+1, j-1]+F[i-1, j+1]+F[i-1, j-1])/h 1/h 2, i=ic+1, …, k 1 -1, j=2, …, jc-1; Центральный баттерфляй: B[ic, jc]=U+(CX[ic+1]-CX[ic])/h 1+(CY[jc+1]-CY[jc])/h 2+(PX[ic-1]PX[ic])/h 1+(PY[jc-1]-PY[jc])/h 2+(C[ic, jc]-C[ic, jc+1]-C[ic+1, jc]+ C[ic+1, jc+1]+S[ic, jc]-S[ic, jc+1]-S[ic-1, jc]+S[ic-1, jc+1]+P[ic, jc]P[ic, jc-1]-P[ic-1, jc]+P[ic-1, jc-1]+F[ic, jc]-F[ic, jc-1]-F[ic+1, jc]+ F[ic+1, jc-1])/h 1/h 2;

Двумерный рынок опционов Пример. Определение оптимального портфеля при {p. S, c. B} p. S = {0. 0179918, 0. 0286584, 0. 032214, 0. 0286584, 0. 0179918, 0. 0278683, 0. 038535, 0. 0420905, 0. 038535, 0. 0278683, 0. 0328066, 0. 0434733, 0. 0470288, 0. 0434733, 0. 0328066, 0. 0434733, 0. 0470288, 0. 0434733, 0. 0328066, 0. 0278683, 0. 038535, 0. 0420905, 0. 038535, 0. 0278683, 0. 0179918, 0. 0286584, 0. 032214, 0. 0286584, 0. 0179918}; c. B = {0. 0292284, 0. 0347617, 0. 0384951, 0. 0400951, 0. 0396728, 0. 0298765, 0. 0354099, 0. 0391432, 0. 0407432, 0. 040321, 0. 0291358, 0. 0346691, 0. 0384025, 0. 0400025, 0. 0395802, 0. 0269136, 0. 0324469, 0. 0361802, 0. 0377802, 0. 037358, 0. 0232099, 0. 0287432, 0. 0324765, 0. 0340765, 0. 0336543, 0. 0183025, 0. 0238358, 0. 0275691, 0. 0291691, 0. 0287469}. ξ = {5, 1, 30, 10, 4, 2, 25, 15, 3, 20, 6, 9, 26, 8, 14, 7, 11, 24, 19, 28, 21, 27, 16, 13, 12, 23, 18, 17, 22}; g = {0. 00129482, 0. 0193656, 0. 0538469, 0. 0122107, 0. 000323704, 0. 0856875, 0. 252012, 0. 1764, 0. 109733, 0. 00669838, 0. 286027, 0. 68703, 0. 616852, 0. 214807, 0. 0399342, 0. 545191, 0. 924415, 0. 842709, 0. 380471, 0. 0701487, 0. 458201, 1. , 0. 758576, 0. 32873, 0. 0278986, 0. 142816, 0. 49782, 0. 421249, 0. 129541, 0. 00291333}

Двумерный рынок опционов Пример. Оптимальный портфель в терминах -опционов C и опционов CX и CY при p = p. S, c = c. B. G = i I, j J gij B[i, j] = 0. 00129482 U+1. 1119 C[1, 1]-1. 93761 C[1, 2] +0. 637968 C[1, 3]-0. 495872 C[1, 4]+0. 683605 C[1, 5]+0. 648179 C[2, 1]+0. 218282 C[2, 2]-3. 19406 C[2, 3]+2. 47241 C[2, 4]0. 144813 C[2, 5]-1. 92342 C[3, 1]+1. 7962 C[3, 2]+2. 1911 C[3, 3]2. 54095 C[3, 4]+0. 477073 C[3, 5]+1. 38265 C[4, 1]-2. 49407 C[4, 2]+1. 80581 C[4, 3]+0. 392654 C[4, 4]-1. 08705 C[4, 5]2. 62027 C[5, 1]+5. 05454 C[5, 2]-1. 64117 C[5, 3]+0. 442252 C[5, 4]-1. 23535 C[5, 5]+1. 40096 C[6, 1]-2. 63735 C[6, 2]+ 0. 200356 C[6, 3]-0. 270493 C[6, 4]+1. 30653 C[6, 5]+0. 253178 CX[1]+0. 34784 CX[2]+0. 176474 CX[3]-1. 03846 CX[4]-0. 685186 CX[5]+0. 946156 CX[6]+0. 0451771 CY[1]+0. 0410261 CY[2]0. 190294 CY[3]+0. 074373 CY[4]+0. 0297175 CY[5].

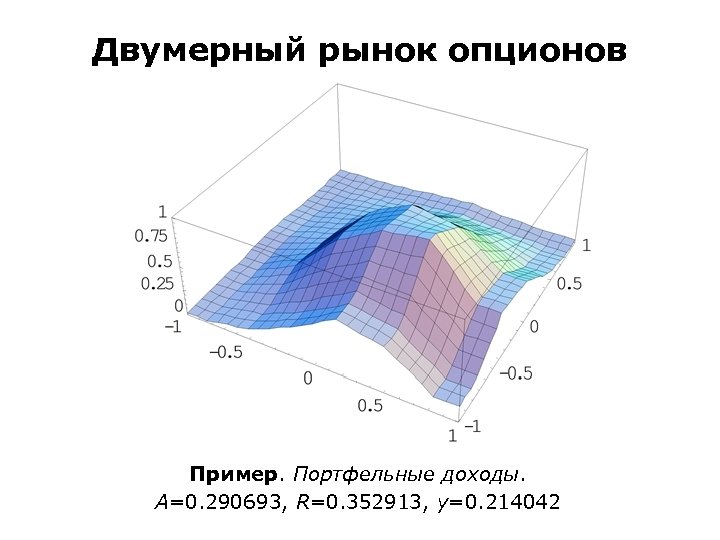Двумерный рынок опционов Пример. Портфельные доходы. A=0. 290693, R=0. 352913, y=0. 214042

Двумерный рынок опционов Пример. Определение оптимального портфеля при {p. B, c. B} X=Y=[-1, 1]; x, s X; y, t Y; p(x, y) = 13/36 - x 2/6 - y 2/6; c(x, y) = 37/120 - (x+1/2)2/20 - (y-1/2)2/20. |CP(s, t)| = (1 -s)2(1 -t)2(7 -2 s-s 2 -2 t-t 2)/144; |CPX(s)| = (1 -s)2(8 -2 s-s 2)/36; |CPY(t)| = (1 -t)2(8 -2 t-t 2)/36. p. B = {0. 0188477, 0. 0287737, 0. 0323292, 0. 0287737, 0. 0188477, 0. 028107, 0. 0380329, 0. 0415885, 0. 0380329, 0. 028107, 0. 0330453, 0. 0429712, 0. 0465267, 0. 0429712, 0. 0330453, 0. 0429712, 0. 0465267, 0. 0429712, 0. 0330453, 0. 028107, 0. 0380329, 0. 0415885, 0. 0380329, 0. 028107, 0. 0188477, 0. 0287737, 0. 0323292, 0. 0287737, 0. 0188477}; c. B = {0. 0292284, 0. 0347617, 0. 0384951, 0. 0400951, 0. 0396728, 0. 0298765, 0. 0354099, 0. 0391432, 0. 0407432, 0. 040321, 0. 0291358, 0. 0346691, 0. 0384025, 0. 0400025, 0. 0395802, 0. 0269136, 0. 0324469, 0. 0361802, 0. 0377802, 0. 037358, 0. 0232099, 0. 0287432, 0. 0324765, 0. 0340765, 0. 0336543, 0. 0183025, 0. 0238358, 0. 0275691, 0. 0291691, 0. 0287469}. ξ = {5, 1, 30, 10, 4, 2, 15, 25, 3, 20, 9, 6, 29, 26, 8, 7, 14, 24, 11, 19, 28, 27, 21, 13, 16, 12, 23, 18, 22, 17};

Двумерный рынок опционов Определение суррогатных вероятностей для базисных баттерфляев взвешенным интегрированием плотности p(x, y) с их платежными функциями в качестве весовых функций; X = [a 1, b 1], Y = [a 2, b 2].

Двумерный рынок опционов Пример. Оптимальный портфель в терминах -опционов C и опционов CX и CY при p = p. B, c = c. B. g = {0. 00129482, 0. 0193656, 0. 0538469, 0. 0122107, 0. 000323704, 0. 109733, 0. 210254, 0. 1764, 0. 0920461, 0. 00669838, 0. 32873, 0. 68703, 0. 566396, 0. 252012, 0. 0295727, 0. 616852, 1. 0, 0. 842709, 0. 380471, 0. 0701487, 0. 49782, 0. 914943, 0. 758576, 0. 292187, 0. 0399342, 0. 142816, 0. 459271, 0. 421249, 0. 129541, 0. 00291333} G = i I, j J gij B[i, j] = 0. 00129482 U + 0. 618381 C[1, 1] - 1. 1309 C[1, 2] + 0. 192134 C[1, 3] - 0. 230572 C[1, 4] + 0. 550955 C[1, 5] + 1. 31495 C[2, 1] - 1. 45328 C[2, 2] - 1. 26651 C[2, 3] + 0. 927604 C[2, 4] + 0. 477234 C[2, 5] - 1. 74697 C[3, 1] + 2. 12289 C[3, 2] + 0. 240391 C[3, 3] - 0. 247238 C[3, 4] - 0. 369071 C[3, 5] + 0. 0684481 C[4, 1] + 0. 213412 C[4, 2] + 0. 795916 C[4, 3] + 0. 0168603 C[4, 4] - 1. 09464 C[4, 5] - 1. 00982 C[5, 1] + 1. 89047 C[5, 2] + 0. 460589 C[5, 3] - 0. 834573 C[5, 4] - 0. 506671 C[5, 5] + 0. 755007 C[6, 1] - 1. 64259 C[6, 2] - 0. 422523 C[6, 3] + 0. 367919 C[6, 4] + 0. 94219 C[6, 5] + 0. 325314 CX[1] + 0. 331678 CX[2] + 0. 207374 CX[3] - 1. 22146 CX[4] - 0. 707919 CX[5] + 1. 06501 CX[6] + 0. 0451771 CY[1] + 0. 0410261 CY[2] - 0. 190294 CY[3] + 0. 074373 CY[4] + 0. 0297175 CY[5].

Двумерный рынок опционов Пример. Оптимальный портфель в терминах -опционов F и опционов FX и FY при {p. S, c. B} G = i I, j J gij B[i, j] = 0. 000323704 U + 1. 1119 F[1, 1] - 1. 93761 F[1, 2] + 0. 637968 F[1, 3] - 0. 495872 F[1, 4] + 0. 683605 F[1, 5] + 0. 648179 F[2, 1] + 0. 218282 F[2, 2] - 3. 19406 F[2, 3] + 2. 47241 F[2, 4] - 0. 144813 F[2, 5] - 1. 92342 F[3, 1] + 1. 7962 F[3, 2] + 2. 1911 F[3, 3] - 2. 54095 F[3, 4] + 0. 477073 F[3, 5] + 1. 38265 F[4, 1] - 2. 49407 F[4, 2] + 1. 80581 F[4, 3] + 0. 392654 F[4, 4] - 1. 08705 F[4, 5] - 2. 62027 F[5, 1] + 5. 05454 F[5, 2] - 1. 64117 F[5, 3] + 0. 442252 F[5, 4] - 1. 23535 F[5, 5] + 1. 40096 F[6, 1] - 2. 63735 F[6, 2] + 0. 200356 F[6, 3] - 0. 270493 F[6, 4] + 1. 30653 F[6, 5] + 0. 019124 FX[1] + 0. 0805834 FX[2] - 0. 00906392 FX[3] - 0. 217394 FX[4] + 0. 0517943 FX[5] + 0. 0749559 FX[6] + 0. 0451771 FY[1] + 0. 0410261 FY[2] - 0. 190294 FY[3] + 0. 074373 FY[4] + 0. 0297175 FY[5]; [GF]= [GC].

Двумерный рынок опционов Пример. Оптимальный портфель в терминах -опционов C, S, P, F и опционов CX, CY, PX, PY при {p. S, c. B}; ic = 3, jc = 3. G = i I, j J gij B[i, j] = 0. 616852 U-0. 451454 C[3, 3]-0. 564412 C[3, 4] +1. 01587 C[3, 5]+0. 694391 C[4, 3]+0. 392654 C[4, 4]-1. 08705 C[4, 5]+0. 793098 C[5, 3]+0. 442252 C[5, 4]-1. 23535 C[5, 5]1. 03604 C[6, 3]-0. 270493 C[6, 4]+1. 30653 C[6, 5]+ 0. 677571 CX[3]-0. 929968 CX[4]-0. 759585 CX[5]+1. 01198 CX[6] -1. 00511 CY[3]+0. 567928 CY[4]+0. 437183 CY[5]-0. 163338 F[3, 1]+0. 0768748 F[3, 2]+0. 0864635 F[3, 3]+1. 38265 F[4, 1]2. 49407 F[4, 2]+1. 11142 F[4, 3]-2. 62027 F[5, 1]+5. 05454 F[5, 2]2. 43427 F[5, 3]+1. 40096 F[6, 1]-2. 63735 F[6, 2]+1. 23639 F[6, 3]+1. 1119 P[1, 1]-1. 93761 P[1, 2]+0. 825702 P[1, 3]+ 0. 648179 P[2, 1]+0. 218282 P[2, 2]-0. 866461 P[2, 3]-1. 76008 P[3, 1]+1. 71932 P[3, 2]+0. 0407597 P[3, 3]+0. 367659 PX[1]+ 0. 953696 PX[2]-1. 32136 PX[3]+1. 00251 PY[1]-1. 17795 PY[2]+ 0. 175444 PY[3]-0. 187733 S[1, 3]-0. 495872 S[1, 4]+0. 683605 S[1, 5]-2. 3276 S[2, 3]+2. 47241 S[2, 4]-0. 144813 S[2, 5]+2. 51533 S[3, 3]-1. 97654 S[3, 4]-0. 538792 S[3, 5]; [G]= [GF]= [GC].

Трехмерный рынок опционов

Трехмерный рынок опционов Пример. Формирование данных X=Y=Z=[– 1, 1]; x, r X; y, s Y; z, t Z. p(x, y, z) = 7/40 – x 2/20 – y 2/20 – z 2/20; c(x, y, z) = 27/160 – (x+1/2)2/40 – (y– 1/2)2/40 – (z– 1/2)2/40; |C(r, s, t)| = [(x–r)(y–s)(z–t) c(x, y, z), {x, r, 1}, {y, s, 1}, {z, t, 1}] = = (1–r)2(1–s)2(1–t)2(31– 4 r–r 2–s 2–t 2)/1920; |CXY(r, s)| = [(x–r)(y–s) c(x, y, z), {x, r, 1}, {y, s, 1}, {z, – 1, 1}] = = (1–r)2(1–s)2(28– 4 r–r 2–s 2)/480; |CXZ(r, t)| = (1–r)2(1+t)2(28– 4 r–r 2–t 2)/480; |CYZ(s, t)| = (1–s)2(1–t)2(36–s 2–t 2)/480; |CX(r)| = [(x–r) c(x, y, z), {x, r, 1}, {y, – 1, 1}, {z, – 1, 1}] = = (1–r)2(25– 4 r–r 2)/120; |CY(s)| = (1–s)2(33–s 2)/120; |CZ(t)| = (1–t)2(33–t 2)/120. Свойство: ρ(x, y, z) = p(x, y, z)/c(x, y, z) (+1, – 1).

Трехмерный рынок опционов Пример. Базисные баттерфляи B C (всего 27 вариантов: 8 вершинных, 12 реберных, 6 граневых, 1 внутренний) B[1, 1, 1]=U+(CX[2]–CX[1])/h 1+(CY[2]–CY[1])/h 2+(CZ[2]–CZ[1])/h 3 +(CXY[1, 1]–CXY[2, 1]–CXY[1, 2]+CXY[2, 2])/h 1/h 2+(CXZ[1, 1]– CXZ[2, 1]–CXZ[1, 2]+ CXZ[2, 2])/h 1/h 3+(CYZ[1, 1]–CYZ[2, 1]– CYZ[1, 2]+CYZ[2, 2])/h 2/h 3+(–C[1, 1, 1]+C[2, 1, 1]+C[1, 2, 1]+ C[1, 1, 2]–C[2, 2, 1]–C[2, 1, 2]–C[1, 2, 2]+C[2, 2, 2])/h 1/h 2/h 3; . . . B[k 1, k 2, k 3]=(–C[k 1, k 2, k 3]+C[k 1– 1, k 2, k 3]+C[k 1, k 2– 1, k 3]+ C[k 1, k 2, k 3– 1]–C[k 1– 1, k 2– 1, k 3]–C[k 1– 1, k 2, k 3– 1]–C[k 1, k 2– 1, k 3– 1]+ C[k 1– 1, k 2– 1, k 3– 1])/h 1/h 2/h 3; . . . B[i, j, k]=(– 8 C[i, j, k]+4 C[i+1, j, k]+4 C[i– 1, j, k]+4 C[i, j+1, k]+4 C[i, j– 1, k] + 4 C[i, j, k+1]+4 C[i, j, k– 1]– 2 C[i+1, j+1, k]– 2 C[i+1, j– 1, k]– 2 C[i– 1, j+1, k]– 2 C[i– 1, j– 1, k]– 2 C[i, j+1, k+1]– 2 C[i, j+1, k– 1]– 2 C[i, j– 1, k+1] – 2 C[i, j– 1, k– 1]– 2 C[i+1, j, k+1]– 2 C[i+1, j, k– 1]– 2 C[i– 1, j, k+1]– 2 C[i– 1, j, k– 1]+C[i+1, j+1, k+1]+C[i+1, j+1, k– 1]+C[i+1, j– 1, k+1]+ C[i+1, j– 1, k– 1]+C[i– 1, j+1, k+1]+C[i– 1, j+1, k– 1]+C[i– 1, j– 1, k+1]+ C[i– 1, j– 1, k– 1])/h 1/h 2/h 3, i=2, …, k 1– 1, j=2, …, k 2– 1, k=2, …, k 3– 1.

Трехмерный рынок опционов Пример. Определение оптимального портфеля при (ε)= ε 2 p = {0. 00738436, 0. 00935967, 0. 00738436, 0. 0095177, 0. 011493, 0. 0095177, 0. 0102288, 0. 0122041, 0. 0102288, 0. 0095177, 0. 011493, 0. 0095177, 0. 00738436, 0. 00935967, 0. 00738436, 0. 00935967, 0. 011335, 0. 00935967, 0. 011493, 0. 0134683, 0. 011493, 0. 0122041, 0. 0141794, 0. 0122041, 0. 011493, 0. 0134683, 0. 011493, 0. 00935967, 0. 011335, 0. 00935967, 0. 0103473, 0. 0123226, 0. 0103473, 0. 0124807, 0. 014456, 0. 0124807, 0. 0131918, 0. 0151671, 0. 0131918, 0. 0124807, 0. 014456, 0. 0124807, 0. 0103473, 0. 0123226, 0. 0103473, 0. 00935967, 0. 011335, 0. 00935967, 0. 011493, 0. 0134683, 0. 011493, 0. 0122041, 0. 0141794, 0. 0122041, 0. 011493, 0. 0134683, 0. 011493, 0. 00935967, 0. 011335, 0. 00935967, 0. 00738436, 0. 00935967, 0. 00738436, 0. 0095177, 0. 011493, 0. 0095177, 0. 0102288, 0. 0122041, 0. 0102288, 0. 0095177, 0. 011493, 0. 0095177, 0. 00738436, 0. 00935967, 0. 00738436}

Трехмерный рынок опционов Пример. Определение оптимального портфеля при (ε)= ε 2 c = {0. 00803498, 0. 0103189, 0. 0108745, 0. 00987942, 0. 0121634, 0. 0127189, 0. 0111239, 0. 0134078, 0. 0139634, 0. 0116572, 0. 0139412, 0. 0144967, 0. 0115165, 0. 0138004, 0. 014356, 0. 00825103, 0. 010535, 0. 0110905, 0. 0100955, 0. 0123794, 0. 012935, 0. 0113399, 0. 0136239, 0. 0141794, 0. 0118733, 0. 0141572, 0. 0147128, 0. 0117325, 0. 0140165, 0. 014572, 0. 00800412, 0. 0102881, 0. 0108436, 0. 00984856, 0. 0121325, 0. 0126881, 0. 011093, 0. 013377, 0. 0139325, 0. 0116263, 0. 0139103, 0. 0144658, 0. 0114856, 0. 0137695, 0. 0143251, 0. 00726337, 0. 00954733, 0. 0101029, 0. 00910782, 0. 0113918, 0. 0119473, 0. 0103523, 0. 0126362, 0. 0131918, 0. 0108856, 0. 0131695, 0. 0137251, 0. 0107449, 0. 0130288, 0. 0135844, 0. 00602881, 0. 00831276, 0. 00886831, 0. 00787325, 0. 0101572, 0. 0107128, 0. 0091177, 0. 0114016, 0. 0119572, 0. 00965103, 0. 011935, 0. 0124905, 0. 00951029, 0. 0117942, 0. 0123498, 0. 004393, 0. 00667695, 0. 00723251, 0. 00623745, 0. 0085214, 0. 00907695, 0. 00748189, 0. 00976584, 0. 0103214, 0. 00801523, 0. 0102992, 0. 0108547, 0. 00787449, 0. 0101584, 0. 010714}

Трехмерный рынок опционов Пример. Определение оптимального портфеля при (ε)= ε 2 ξ ={15, 13, 30, 12, 14, 3, 90, 45, 9, 6, 75, 60, 27, 28, 29, 10, 11, 18, 24, 42, 87, 21, 44, 43, 2, 57, 8, 1, 7, 72, 89, 88, 5, 59, 39, 26, 33, 74, 58, 4, 25, 36, 73, 84, 54, 69, 78, 41, 23, 51, 81, 63, 66, 40, 17, 22, 20, 56, 86, 71, 38, 16, 19, 55, 85, 37, 70, 35, 32, 53, 68, 83, 34, 50, 52, 47, 31, 65, 67, 80, 62, 82, 49, 77, 46, 64, 79, 61, 76} g = {0. 0783594, 0. 0614338, 0. 00253916, 0. 168442, 0. 108825, 0. 00772084, 0. 0841907, 0. 0742798, 0. 00613882, 0. 0222847, 0. 0258482, 0. 00113206, 0. 000218115, 0. 0018495, 0. 0000545288, 0. 465158, 0. 350948, 0. 0289454, 0. 480967, 0. 382024, 0. 0465821, 0. 365556, 0. 276404, 0. 0332469, 0. 178008, 0. 136064, 0. 0141773, 0. 0164937, 0. 0195337, 0. 000582179, 0. 759213, 0. 588257, 0. 143805, 0. 674059, 0. 569507, 0. 188695, 0. 531015, 0. 452478, 0. 12631, 0. 337646, 0. 261696, 0. 0379541, 0. 0568817, 0. 0520531, 0. 00464058, 0. 925916, 0. 741288, 0. 247115, 0. 888378, 0. 698005, 0. 289683, 0. 720221, 0. 611753, 0. 218248, 0. 498434, 0. 400103, 0. 0677764, 0. 16072, 0. 117107, 0. 0115724, 0. 985286, 0. 846085, 0. 31036, 0. 948166, 0. 782865, 0. 323298, 0. 80461, 0. 634135, 0. 2298, 0. 547897, 0. 432304, 0. 0909924, 0. 196914, 0. 15253, 0. 00945328, 1. , 0. 90611, 0. 236934, 0. 966792, 0. 825361, 0. 300019, 0. 865007, 0. 653721, 0. 206097, 0. 511963, 0. 414774, 0. 0417531, 0. 101374, 0. 0967266, 0. 00333789}

Трехмерный рынок опционов Пример. Оптимальный портфель в терминах -опционов C и опционов CXY, CXZ, CYZ, CX, CY, CZ. G = i, j, k gijk. B[i, j, k] = 0. 0783594 U+0. 652028 C[1, 1, 1]– 0. 328364 C[1, 1, 2]– 0. 323664 C[1, 1, 3]– 1. 10107 C[1, 2, 1]+1. 44477 C[1, 2, 2] – 0. 343699 C[1, 2, 3]+0. 82855 C[1, 3, 1]– 0. 620154 C[1, 3, 2]– 0. 208396 C[1, 3, 3]+0. 148284 C[1, 4, 1]– 0. 123879 C[1, 4, 2]– 0. 0244049 C[1, 4, 3]– 0. 527796 C[1, 5, 1]– 0. 372368 C[1, 5, 2]+0. 900163 C[1, 5, 3]– 0. 0767373 C[2, 1, 1]+0. 62022 C[2, 1, 2]– 0. 543483 C[2, 1, 3]+0. 708291 C[2, 2, 1]– 2. 3426 C[2, 2, 2]+1. 6343 C[2, 2, 3]– 1. 51307 C[2, 3, 1]+1. 51614 C[2, 3, 2]– 0. 00307589 C[2, 3, 3]+0. 647775 C[2, 4, 1]+0. 365485 C[2, 4, 2]– 1. 01326 C[2, 4, 3]+0. 233736 C[2, 5, 1]– 0. 15925 C[2, 5, 2]– 0. 0744859 C[2, 5, 3]– 1. 38698 C[3, 1, 1]+0. 769723 C[3, 1, 2]+ 0. 617259 C[3, 1, 3]+1. 83324 C[3, 2, 1]– 1. 24058 C[3, 2, 2]– 0. 592661 C[3, 2, 3]+0. 140683 C[3, 3, 1]– 0. 368137 C[3, 3, 2]+ 0. 227454 C[3, 3, 3]– 1. 06554 C[3, 4, 1]+1. 05961 C[3, 4, 2]+ 0. 00592486 C[3, 4, 3]+0. 478598 C[3, 5, 1]– 0. 220621 C[3, 5, 2]– 0. 257976 C[3, 5, 3]+0. 582709 C[4, 1, 1]– 0. 941666 C[4, 1, 2]+ 0. 358957 C[4, 1, 3]– 2. 19114 C[4, 2, 1]+3. 45283 C[4, 2, 2] – 1. 2617 C[4, 2, 3]+2. 02687 C[4, 3, 1]– 2. 44481 C[4, 3, 2] + 0. 417943 …

Трехмерный рынок опционов … C[4, 3, 3]– 0. 0483658 C[4, 4, 1]– 1. 3254 C[4, 4, 2]+ 1. 37377 C[4, 4, 3]– 0. 370073 C[4, 5, 1]+1. 25905 C[4, 5, 2]– 0. 888973 C[4, 5, 3]– 0. 0122262 C[5, 1, 1]+0. 882652 C[5, 1, 2]– 0. 870426 C[5, 1, 3]+0. 264223 C[5, 2, 1]– 1. 33637 C[5, 2, 2]+ 1. 07215 C[5, 2, 3]– 0. 0892028 C[5, 3, 1]+0. 400438 C[5, 3, 2]– 0. 311235 C[5, 3, 3]– 0. 108355 C[5, 4, 1]+1. 23585 C[5, 4, 2]– 1. 12749 C[5, 4, 3] – 0. 0544399 C[5, 5, 1]– 1. 18256 C[5, 5, 2]+1. 237 C[5, 5, 3] +0. 241208 C[6, 1, 1]– 1. 00256 C[6, 1, 2] +0. 761356 C[6, 1, 3] +0. 486448 C[6, 2, 1]+0. 0219495 C[6, 2, 2]– 0. 508398 C[6, 2, 3]– 1. 39383 C[6, 3, 1]+1. 51652 C[6, 3, 2]– 0. 122691 C[6, 3, 3] + 0. 4262 C[6, 4, 1]– 1. 21166 C[6, 4, 2]+0. 785463 C[6, 4, 3]+ 0. 239974 C[6, 5, 1]+0. 675756 C[6, 5, 2]– 0. 91573 C[6, 5, 3]+ 1. 16039 CX[1]– 0. 278228 CX[2]– 0. 382058 CX[3]– 0. 321999 CX[4]– 0. 133967 CX[5]– 0. 0441426 CX[6]– 0. 557048 CXY[1, 1]+ 0. 32335 CXY[1, 2]– 0. 70862 CXY[1, 3]– 0. 103536 CXY[1, 4]+ 1. 04585 CXY[1, 5]– 0. 20018 CXY[2, 1]+0. 226632 CXY[2, 2]+ 0. 872213 CXY[2, 3]– 0. 74719 CXY[2, 4]– 0. 151475 CXY[2, 5]+ 1. 11436 CXY[3, 1]– 1. 09546 CXY[3, 2]– 0. 188378 CXY[3, 3]+ 0. 636744 CXY[3, 4]– 0. 467259 CXY[3, 5]– 0. 353993 CXY[4, 1]+ …

Трехмерный рынок опционов … +0. 726858 CXY[4, 2]– 0. 421669 CXY[4, 3]+0. 376403 CXY[4, 4]– 0. 327599 CXY[4, 5]+0. 0262043 CXY[5, 1]+0. 102564 CXY[5, 2]– 0. 589306 CXY[5, 3]+ 0. 113018 CXY[5, 4] +0. 34752 CXY[5, 5]– 0. 0293391 CXY[6, 1]– 0. 28394 CXY[6, 2]+ 1. 03576 CXY[6, 3]– 0. 275439 CXY[6, 4]– 0. 447041 CXY[6, 5]– 0. 43778 CXZ[1, 1]– 0. 746203 CXZ[1, 2]+1. 18398 CXZ[1, 3]+ 0. 182425 CXZ[2, 1]+ 0. 450533 CXZ[2, 2]– 0. 632958 CXZ[2, 3]+ 0. 193832 CXZ[3, 1]+ 0. 133447 CXZ[3, 2]– 0. 327279 CXZ[3, 3]+ 0. 265944 CXZ[4, 1]– 0. 229177 CXZ[4, 2]– 0. 0367664 CXZ[4, 3]– 0. 000523427 CXZ[5, 1]– 0. 413023 CXZ[5, 2]+0. 413546 CXZ[5, 3]– 0. 203897 CXZ[6, 1]+ 0. 804424 CXZ[6, 2]– 0. 600527 CXZ[6, 3]+ 0. 225206 CY[1]– 0. 435833 CY[2]+0. 0558623 CY[3]+0. 0995985 CY[4]+0. 0551665 CY[5]– 0. 160091 CYZ[1, 1]+ 0. 00180529 CYZ[1, 2]+ 0. 158286 CYZ[1, 3]+0. 346488 CYZ[2, 1]– 0. 0645896 CYZ[2, 2]– 0. 281898 CYZ[2, 3]– 0. 135867 CYZ[3, 1]+ 0. 175099 CYZ[3, 2]– 0. 0392312 CYZ[3, 3]– 0. 0577742 CYZ[4, 1]– 0. 0191148 CYZ[4, 2]+ 0. 076889 CYZ[4, 3]+0. 00724528 CYZ[5, 1]– 0. 0931996 CYZ[5, 2]+ 0. 0859543 CYZ[5, 3]– 0. 0253885 CZ[1]– 0. 0629535 CZ[2]+ 0. 088342 CZ[3]. (Всего k 1 k 2 k 3+k 1 k 2+k 1 k 3+k 2 k 3+k 1+k 2+k 3+1=168 компонент)

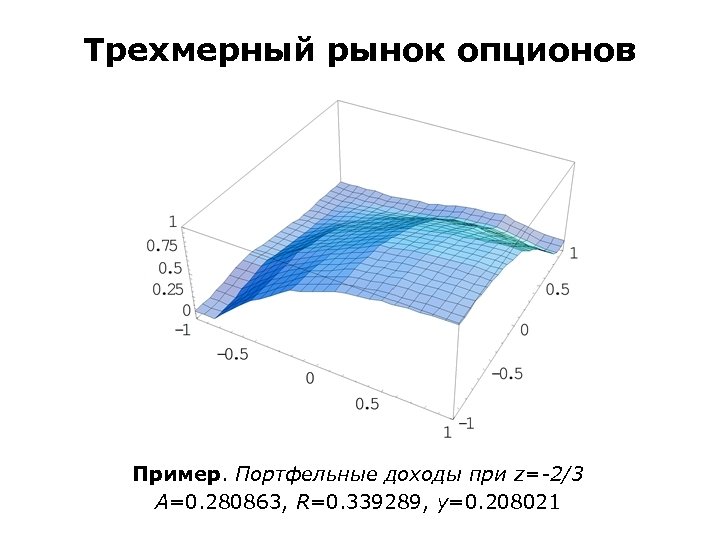Трехмерный рынок опционов Пример. Портфельные доходы при z=-2/3 A=0. 280863, R=0. 339289, y=0. 208021

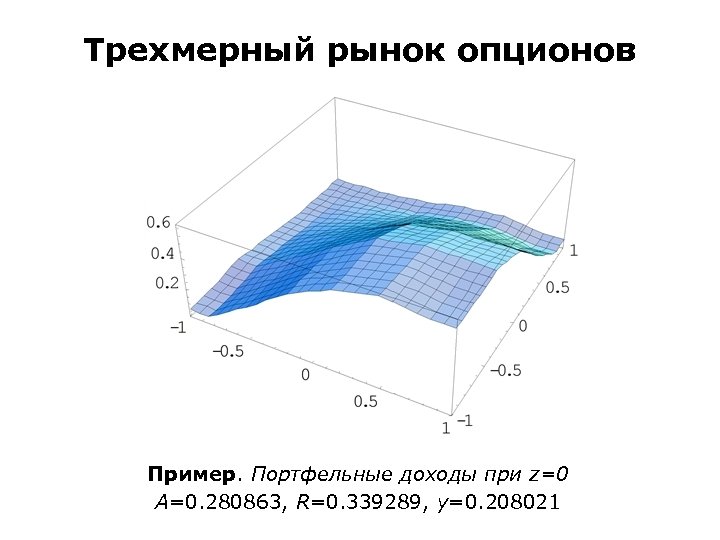Трехмерный рынок опционов Пример. Портфельные доходы при z=0 A=0. 280863, R=0. 339289, y=0. 208021

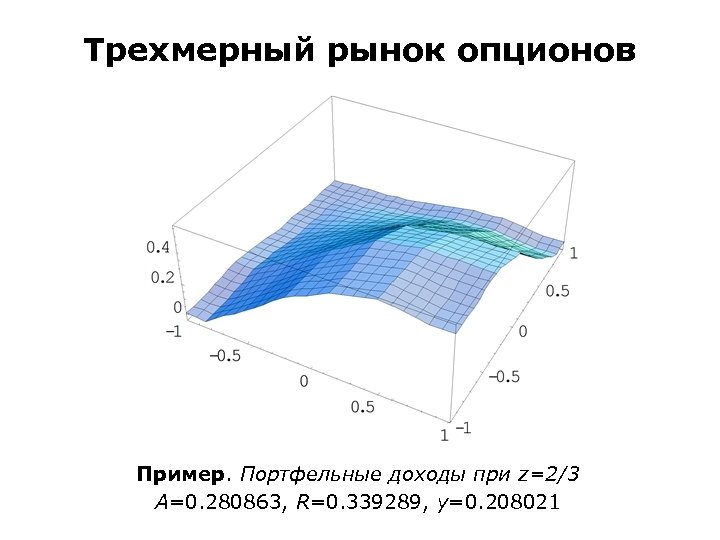Трехмерный рынок опционов Пример. Портфельные доходы при z=2/3 A=0. 280863, R=0. 339289, y=0. 208021

Многомерный рынок опционов

Двумерный рынок опционов

Трехмерный рынок опционов

Многомерный ζ-рынок

Двумерный ζ-рынок

Двумерный ζ-рынок Одномерная преамбула (2 слайда) Сценарные базисы: • α={– 1}; D 1 = Z 0; 1; Di = –Z 0; i– 1 + Z 0; i, 0

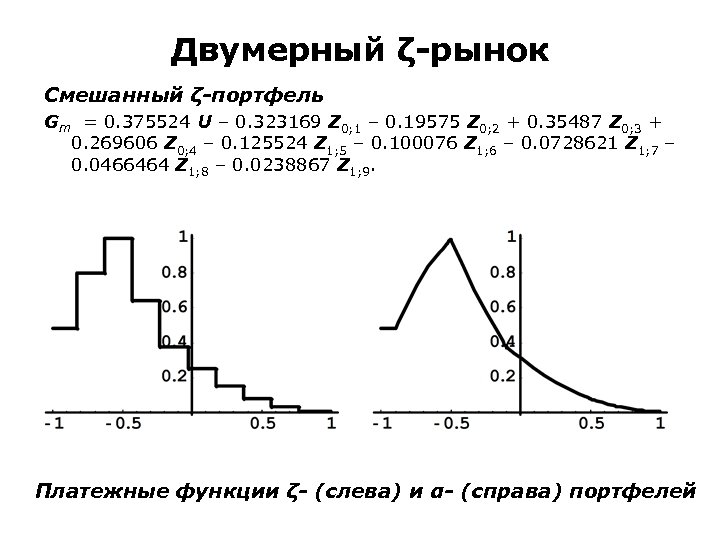Двумерный ζ-рынок Смешанный ζ-портфель Gm = 0. 375524 U – 0. 323169 Z 0; 1 – 0. 19575 Z 0; 2 + 0. 35487 Z 0; 3 + 0. 269606 Z 0; 4 – 0. 125524 Z 1; 5 – 0. 100076 Z 1; 6 – 0. 0728621 Z 1; 7 – 0. 0466464 Z 1; 8 – 0. 0238867 Z 1; 9. Платежные функции ζ- (слева) и α- (справа) портфелей

Двумерный ζ-рынок Однотипные ζ-базисы α = {-1, -1} D 1, 1 = Z 1, 1; D 1, j = –Z 1, j– 1 + Z 1, j; D 1, n 2 = Z 1, ∙ – Z 1, n 2– 1; Di, 1 = –Zi– 1, 1 + Zi, 1; Di, j = Zi– 1, j– 1 – Zi– 1, j – Zi, j– 1 + Zi, j; Di, n 2 = –Zi– 1, ∙ + Zi– 1, n 2– 1 + Zi, ∙ – Zi, n 2– 1; Dn 1, 1 = Z∙, 1 – Zn 1– 1, 1; Dn 1, j = –Z∙, j– 1 + Z∙, j + Zn 1– 1, j– 1 – Zn 1– 1, j; Dn 1, n 2 = U – Z∙, n 2– 1 – Zn 1– 1, ∙ + Zn 1– 1, n 2– 1; α = {-1, +1} D 1, 1 = –Z 1, 1 + Z 1, ∙; D 1, j = Z 1, j– 1 – Z 1, j; D 1, n 2 = Z 1, n 2– 1; Di, 1 = Zi– 1, 1 – Zi– 1, ∙ – Zi, 1 + Zi, ∙; Di, j = –Zi– 1, j– 1 + Zi– 1, j + Zi, j– 1 – Zi, j; Di, n 2 = –Zi– 1, n 2– 1 + Zi, n 2– 1; Dn 1, 1 = U – Z∙, 1 + Zn 1– 1, 1 – Zn 1– 1, ∙; Dn 1, j = Z∙, j– 1 – Z∙, j – Zn 1– 1, j– 1 + Zn 1– 1, j; Dn 1, n 2 = Z∙, n 2– 1 – Zn 1– 1, n 2– 1;

Двумерный ζ-рынок Однотипные ζ-базисы (продолжение) α = {+1, -1} D 1, 1 = –Z 1, 1 + Z∙, 1; D 1, j = Z 1, j– 1 – Z 1, j – Z∙, j– 1 + Z∙, j; D 1, n 2 = U – Z 1, ∙ + Z 1, n 2– 1 – Z∙, n 2– 1; Di, 1 = Zi– 1, 1 – Zi, 1; Di, j = –Zi– 1, j– 1 + Zi– 1, j + Zi, j– 1 – Zi, j; Di, n 2 = Zi– 1, ∙ – Zi– 1, n 2– 1 – Zi, ∙ + Zi, n 2– 1; Dn 1, 1 = Zn 1– 1, 1; Dn 1, j = –Zn 1– 1, j– 1 + Zn 1– 1, j; Dn 1, n 2 = Zn 1– 1, ∙ – Zn 1– 1, n 2– 1; α = {+1, +1} D 1, 1 = U + Z 1, 1 – Z 1, ∙ – Z∙, 1; D 1, j = –Z 1, j– 1 + Z 1, j + Z∙, j– 1 – Z∙, j; D 1, n 2 = –Z 1, n 2– 1 + Z∙, n 2– 1; Di, 1 = –Zi– 1, 1 + Zi– 1, ∙ + Zi, 1 – Zi, ∙; Di, j = Zi– 1, j– 1 – Zi– 1, j – Zi, j– 1 + Zi, j; Di, n 2 = Zi– 1, n 2– 1 – Zi, n 2– 1; Dn 1, 1 = –Zn 1– 1, 1 + Zn 1– 1, ∙; Dn 1, j = Zn 1– 1, j– 1 – Zn 1– 1, j; Dn 1, n 2 = Zn 1– 1, n 2– 1.

Двумерный ζ-рынок Смешанный ζ-базис D 1, 1 = Z 0; 1, 1; D 1, j = –Z 0; 1, j– 1 + Z 0; 1, j, 0

Двумерный ζ-рынок Однотипные ζ-портфели α = {– 1, – 1} G = 0. 00291333 U + 0. 148254 Z 1, 1 – 0. 110094 Z 1, 2 – 0. 0250311 Z 1, 3 – 0. 0911473 Z 1, 4 – 0. 00637467 Z 1, ∙ + 0. 191975 Z 2, 1 – 0. 0450216 Z 2, 2 – 0. 284921 Z 2, 3 – 0. 071839 Z 2, 4 – 0. 0332358 Z 2, ∙ – 0. 0507364 Z 3, 1 + 0. 0389278 Z 3, 2 – 0. 11065 Z 3, 3 – 0. 135449 Z 3, 4 – 0. 0302145 Z 3, ∙ + 0. 194617 Z 4, 1 – 0. 159717 Z 4, 2 – 0. 0041513 Z 4, 3 + 0. 0460336 Z 4, 4 + 0. 0422501 Z 4, ∙ – 0. 185724 Z 5, 1 + 0. 203401 Z 5, 2 + 0. 174681 Z 5, 3 + 0. 137661 Z 5, 4 + 0. 0249853 Z 5, ∙ – 0. 316456 Z∙, 1 + 0. 0380221 Z∙, 2 + 0. 291708 Z∙, 3 + 0. 126627 Z∙, 4; α ={– 1, +1} G = 0. 142816 U – 0. 148254 Z 1, 1 + 0. 110094 Z 1, 2 + 0. 0250311 Z 1, 3 + 0. 0911473 Z 1, 4 – 0. 0843927 Z 1, ∙ – 0. 191975 Z 2, 1 + 0. 0450216 Z 2, 2 + 0. 284921 Z 2, 3 + 0. 071839 Z 2, 4 – 0. 243042 Z 2, ∙ + 0. 0507364 Z 3, 1 – 0. 0389278 Z 3, 2 + 0. 11065 Z 3, 3 + 0. 135449 Z 3, 4 – 0. 288122 Z 3, ∙ – 0. 194617 Z 4, 1 + 0. 159717 Z 4, 2 + 0. 0041513 Z 4, 3 – 0. 0460336 Z 4, 4 + 0. 119032 Z 4, ∙ + 0. 185724 Z 5, 1 – 0. 203401 Z 5, 2 – 0. 174681 Z 5, 3 – 0. 137661 Z 5, 4 + 0. 355005 Z 5, ∙ + 0. 316456 Z∙, 1 – 0. 0380221 Z∙, 2 – 0. 291708 Z∙, 3 – 0. 126627 Z∙, 4; α = {+1, – 1} G = 0. 000323704 U – 0. 148254 Z 1, 1 + 0. 110094 Z 1, 2 + 0. 0250311 Z 1, 3 + 0. 0911473 Z 1, 4 + 0. 00637467 Z 1, ∙ – 0. 191975 Z 2, 1 + 0. 0450216 Z 2, 2 + 0. 284921 Z 2, 3 + 0. 071839 Z 2, 4 + 0. 0332358 Z 2, ∙ + 0. 0507364 Z 3, 1 – 0. 0389278 Z 3, 2 + 0. 11065 Z 3, 3 + 0. 135449 Z 3, 4 + 0. 0302145 Z 3, ∙ – 0. 194617 Z 4, 1 + 0. 159717 Z 4, 2 + 0. 0041513 Z 4, 3 – 0. 0460336 Z 4, 4 – 0. 0422501 Z 4, ∙ + 0. 185724 Z 5, 1 – 0. 203401 Z 5, 2 – 0. 174681 Z 5, 3 – 0. 137661 Z 5, 4 – 0. 0249853 Z 5, ∙ – 0. 0180708 Z∙, 1 – 0. 0344813 Z∙, 2 + 0. 0416362 Z∙, 3 + 0. 011887 Z∙, 4;

Двумерный ζ-рынок Однотипные ζ-портфели(продолжение) α = {+1, +1} G = 0. 00129482 U + 0. 148254 Z 1, 1 – 0. 110094 Z 1, 2 – 0. 0250311 Z 1, 3 – 0. 0911473 Z 1, 4 + 0. 0843927 Z 1, ∙ + 0. 191975 Z 2, 1 – 0. 0450216 Z 2, 2 – 0. 284921 Z 2, 3 – 0. 071839 Z 2, 4 + 0. 243042 Z 2, ∙ – 0. 0507364 Z 3, 1 + 0. 0389278 Z 3, 2 – 0. 11065 Z 3, 3 – 0. 135449 Z 3, 4 + 0. 288122 Z 3, ∙ + 0. 194617 Z 4, 1 – 0. 159717 Z 4, 2 – 0. 0041513 Z 4, 3 + 0. 0460336 Z 4, 4 – 0. 119032 Z 4, ∙ – 0. 185724 Z 5, 1 + 0. 203401 Z 5, 2 + 0. 174681 Z 5, 3 + 0. 137661 Z 5, 4 – 0. 355005 Z 5, ∙ + 0. 0180708 Z∙, 1 + 0. 0344813 Z∙, 2 – 0. 0416362 Z∙, 3 – 0. 011887 Z∙, 4. Смешанный ζ-портфель G = 0. 566396 U – 0. 122553 X 01; 1 – 0. 389996 X 01; 2 – 0. 3583 X 02; 1 + 0. 120634 X 02; 2 + 0. 276313 X 11; 3 – 0. 0841324 X 11; 4 – 0. 337327 X 11; 5 – 0. 351588 X 12; 3 – 0. 174873 X 12; 4 + 0. 148254 Z 0; 1, 1 – 0. 110094 Z 0; 1, 2 + 0. 191975 Z 0; 2, 1 – 0. 0450216 Z 0; 2, 2 + 0. 0250311 Z 1; 1, 3 + 0. 0911473 Z 1; 1, 4 + 0. 284921 Z 1; 2, 3 + 0. 071839 Z 1; 2, 4 + 0. 0507364 Z 2; 3, 1 – 0. 0389278 Z 2; 3, 2 – 0. 194617 Z 2; 4, 1 + 0. 159717 Z 2; 4, 2 + 0. 185724 Z 2; 5, 1 – 0. 203401 Z 2; 5, 2 – 0. 11065 Z 3; 3, 3 – 0. 135449 Z 3; 3, 4 – 0. 0041513 Z 3; 4, 3 + 0. 0460336 Z 3; 4, 4 + 0. 174681 Z 3; 5, 3 + 0. 137661 Z 3; 5, 4.

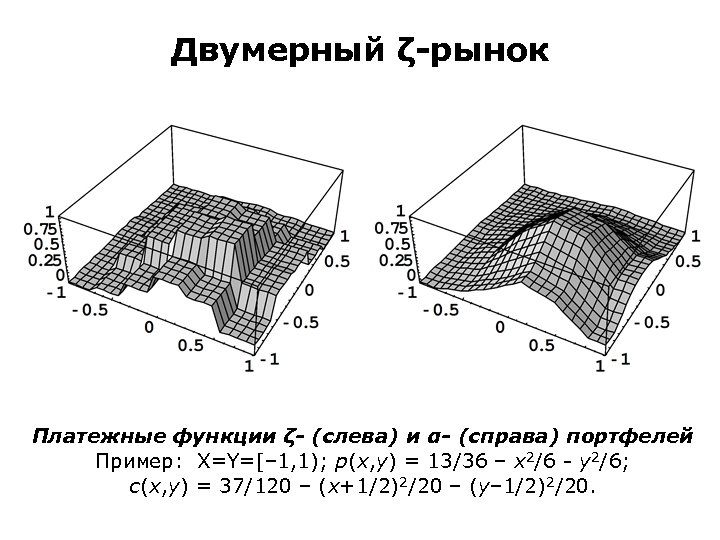Двумерный ζ-рынок Платежные функции ζ- (слева) и α- (справа) портфелей Пример: X=Y=[– 1, 1); p(x, y) = 13/36 – x 2/6 - y 2/6; c(x, y) = 37/120 – (x+1/2)2/20 – (y– 1/2)2/20.

Трехмерный ζ-рынок

Трехмерный ζ-рынок Однотипный базис α = {-1, +1, -1} D 1, 1, 1 = –Z 1, 1, 1 + Z 1, ∙, 1; D 1, 1, k = Z 1, 1, k– 1 – Z 1, 1, k – Z 1, ∙, k– 1 + Z 1, ∙, k; D 1, 1, n 3 = –Z 1, 1, ∙ + Z 1, 1, n 3– 1 + Z 1, ∙, ∙ – Z 1, ∙, n 3– 1; D 1, j, 1 = Z 1, j– 1, 1 – Z 1, j, 1; D 1, j, k = –Z 1, j– 1, k– 1 + Z 1, j– 1, k + Z 1, j, k– 1 – Z 1, j, k; D 1, j, n 3 = Z 1, j– 1, ∙ – Z 1, j– 1, n 3– 1 – Z 1, j, ∙ + Z 1, j, n 3– 1; D 1, n 2, 1 = Z 1, n 2– 1, 1; D 1, n 2, k = –Z 1, n 2– 1, k– 1 + Z 1, n 2– 1, k; D 1, n 2, n 3 = Z 1, n 2– 1, ∙ – Z 1, n 2– 1, n 3– 1; Di, 1, 1 = Zi– 1, 1, 1 – Zi– 1, ∙, 1 – Zi, 1, 1 + Zi, ∙, 1; Di, 1, k = –Zi– 1, 1, k– 1 + Zi– 1, 1, k + Zi– 1, ∙, k– 1 – Zi– 1, ∙, k+ Zi, 1, k– 1 – Zi, 1, k – Zi, ∙, k– 1 + Zi, ∙, k; Di, 1, n 3 = Zi– 1, 1, ∙ – Zi– 1, 1, n 3– 1 – Zi– 1, ∙, ∙ + Zi– 1, ∙, n 3– 1 – Zi, 1, ∙+ Zi, 1, n 3– 1 + Zi, ∙, ∙ – Zi, ∙, n 3– 1; Di, j, 1 = –Zi– 1, j– 1, 1 + Zi– 1, j, 1 + Zi, j– 1, 1 – Zi, j, 1; Di, j, k = Zi– 1, j– 1, k– 1 – Zi– 1, j– 1, k – Zi– 1, j, k– 1 + Zi– 1, j, k– Zi, j– 1, k– 1 + Zi, j– 1, k + Zi, j, k– 1 – Zi, j, k; Di, j, n 3 = –Zi– 1, j– 1, ∙ + Zi– 1, j– 1, n 3– 1 + Zi– 1, j, ∙– Zi– 1, j, n 3– 1 + Zi, j– 1, ∙ – Zi, j– 1, n 3– 1 – Zi, j, ∙+ Zi, j, n 3– 1; Di, n 2, 1 = –Zi– 1, n 2– 1, 1 + Zi, n 2– 1, 1; Di, n 2, k = Zi– 1, n 2– 1, k– 1 – Zi– 1, n 2– 1, k – Zi, n 2– 1, k– 1+ Zi, n 2– 1, k; Di, n 2, n 3 = –Zi– 1, n 2– 1, ∙ + Zi– 1, n 2– 1, n 3– 1+ Zi, n 2– 1, ∙ – Zi, n 2– 1, n 3– 1; Dn 1, 1, 1 = –Z∙, 1, 1 + Z∙, ∙, 1 + Zn 1– 1, 1, 1 – Zn 1– 1, ∙, 1; Dn 1, 1, k = Z∙, 1, k– 1 – Z∙, 1, k – Z∙, ∙, k– 1 + Z∙, ∙, k – Zn 1– 1, 1, k– 1+ Zn 1– 1, 1, k + Zn 1– 1, ∙, k– 1 – Zn 1– 1, ∙, k; Dn 1, 1, n 3 = U – Z∙, 1, ∙ + Z∙, 1, n 3– 1 – Z∙, ∙, n 3– 1 + Zn 1– 1, 1, ∙– Zn 1– 1, 1, n 3– 1 – Zn 1– 1, ∙, ∙ + Zn 1– 1, ∙, n 3– 1; Dn 1, j, 1 = Z∙, j– 1, 1 – Z∙, j, 1 – Zn 1– 1, j– 1, 1 + Zn 1– 1, j, 1; Dn 1, j, k = –Z∙, j– 1, k– 1 + Z∙, j– 1, k + Z∙, j, k– 1 – Z∙, j, k+ Zn 1– 1, j– 1, k– 1 – Zn 1– 1, j– 1, k – Zn 1– 1, j, k– 1+ Zn 1– 1, j, k; Dn 1, j, n 3 = Z∙, j– 1, ∙ – Z∙, j– 1, n 3– 1 – Z∙, j, ∙ + Z∙, j, n 3– 1– Zn 1– 1, j– 1, ∙ + Zn 1– 1, j– 1, n 3– 1 + Zn 1– 1, j, ∙– Zn 1– 1, j, n 3– 1; Dn 1, n 2, 1 = Z∙, n 2– 1, 1 – Zn 1– 1, n 2– 1, 1; Dn 1, n 2, k = –Z∙, n 2– 1, k– 1 + Z∙, n 2– 1, k+ Zn 1– 1, n 2– 1, k– 1 – Zn 1– 1, n 2– 1, k; Dn 1, n 2, n 3 = Z∙, n 2– 1, ∙ – Z∙, n 2– 1, n 3– 1 – Zn 1– 1, n 2– 1, ∙+ Zn 1– 1, n 2– 1, n 3– 1.

Трехмерный ζ-рынок Однотипный портфель α = {-1, +1, -1} G = 0. 289683 U + 0. 0719458 Z 1, 1, 1 + 0. 0272048 Z 1, 1, 2 – 0. 012455 Z 1, 1, ∙ – 0. 0321013 Z 1, 2, 1 + 0. 030143 Z 1, 2, 2 + 0. 0117531 Z 1, 2, ∙ + 0. 0345458 Z 1, 3, 1 + 0. 0890676 Z 1, 3, 2 + 0. 0140629 Z 1, 3, ∙ + 0. 0405706 Z 1, 4, 1 + 0. 079818 Z 1, 4, 2 + 0. 0128194 Z 1, 4, ∙ – 0. 118757 Z 1, ∙, 1 – 0. 241163 Z 1, ∙, 2 – 0. 0264062 Z 1, ∙, ∙ – 0. 0215768 Z 2, 1, 1 + 0. 100317 Z 2, 1, 2 – 0. 024241 Z 2, 1, ∙ + 0. 0680832 Z 2, 2, 1 – 0. 0710925 Z 2, 2, 2 + 0. 0542442 Z 2, 2, ∙ – 0. 0706414 Z 2, 3, 1 – 0. 00383163 Z 2, 3, 2 + 0. 0640917 Z 2, 3, ∙ + 0. 0458567 Z 2, 4, 1 + 0. 0690593 Z 2, 4, 2 + 0. 0194166 Z 2, 4, ∙ – 0. 0414198 Z 2, ∙, 1 – 0. 12514 Z 2, ∙, 2 – 0. 117872 Z 2, ∙, ∙ – 0. 0318548 Z 3, 1, 1 + 0. 00379276 Z 3, 1, 2 – 0. 0000836123 Z 3, 1, ∙ – 0. 0578945 Z 3, 2, 1 + 0. 0736296 Z 3, 2, 2 – 0. 00403864 Z 3, 2, ∙ + 0. 0985276 Z 3, 3, 1 – 0. 128407 Z 3, 3, 2 + 0. 0711606 Z 3, 3, ∙ – 0. 0589642 Z 3, 4, 1 + 0. 0717031 Z 3, 4, 2 + 0. 0190402 Z 3, 4, ∙ + 0. 01891 Z 3, ∙, 1 – 0. 0689503 Z 3, ∙, 2 – 0. 0930104 Z 3, ∙, ∙ – 0. 0370363 Z 4, 1, 1 – 0. 0115829 Z 4, 1, 2 + 0. 0290238 Z 4, 1, ∙ – 0. 0205342 Z 4, 2, 1 – 0. 0355973 Z 4, 2, 2 + 0. 029957 Z 4, 2, ∙ – 0. 0673051 Z 4, 3, 1 + 0. 0659939 Z 4, 3, 2 – 0. 00519868 Z 4, 3, ∙ + 0. 0658495 Z 4, 4, 1 – 0. 018446 Z 4, 4, 2 + 0. 0188696 Z 4, 4, ∙ + 0. 0454268 Z 4, ∙, 1 – 0. 0342641 Z 4, ∙, 2 – 0. 0705325 Z 4, ∙, ∙ – 0. 025263 Z 5, 1, 1 + 0. 0187494 Z 5, 1, 2 + 0. 00260173 Z 5, 1, ∙ – 0. 063479 Z 5, 2, 1 + 0. 0102523 Z 5, 2, 2 + 0. 00883539 Z 5, 2, ∙ + 0. 0111043 Z 5, 3, 1 + 0. 0303057 Z 5, 3, 2 + 0. 00680955 Z 5, 3, ∙ + 0. 03298 Z 5, 4, 1 + 0. 0681921 Z 5, 4, 2 – 0. 0328081 Z 5, 4, ∙ + 0. 0453105 Z 5, ∙, 1 – 0. 0807015 Z 5, ∙, 2 + 0. 0206768 Z 5, ∙, ∙ + 0. 0695667 Z∙, 1, 1 – 0. 11311 Z∙, 1, 2 + 0. 0103359 Z∙, 1, ∙ + 0. 0712005 Z∙, 2, 1 – 0. 0472814 Z∙, 2, 2 – 0. 102333 Z∙, 2, ∙ – 0. 0376786 Z∙, 3, 1 – 0. 0830138 Z∙, 3, 2 – 0. 155933 Z∙, 3, ∙ – 0. 13053 Z∙, 4, 1 – 0. 290278 Z∙, 4, 2 – 0. 0384152 Z∙, 4, ∙ + 0. 0938903 Z∙, ∙, 1 + 0. 616427 Z∙, ∙, 2.

Трехмерный ζ-рынок Смешанный портфель G = 0. 452478 U + 0. 0245874 X 01; 1, 1 + 0. 0707072 X 01; 2, 1 – 0. 0789124 X 02; 1, 1 + 0. 00508658 X 02; 2, 1 – 0. 0147498 X 03; 1, 1 – 0. 0418961 X 03; 1, 2 – 0. 076076 X 03; 2, 1 + 0. 0168483 X 03; 2, 2 – 0. 102151 X 11; 1, 2 + 0. 00100312 X 11; 2, 2 + 0. 183815 X 12; 1, 2 + 0. 0959155 X 12; 2, 2 + 0. 103131 X 13; 1, 3 + 0. 0926374 X 13; 1, 4 + 0. 0602601 X 13; 2, 3 + 0. 0884759 X 13; 2, 4 + 0. 00464822 X 21; 3, 1 – 0. 0906644 X 21; 4, 1 + 0. 0708394 X 22; 3, 1 + 0. 0121438 X 22; 4, 1 + 0. 0434315 X 22; 5, 1 + 0. 00370915 X 23; 3, 1 + 0. 0695909 X 23; 3, 2 + 0. 0174409 X 23; 4, 1 – 0. 00564038 X 23; 4, 2 + 0. 0213511 X 23; 5, 1 + 0. 0190877 X 23; 5, 2 + 0. 115122 X 31; 3, 2 + 0. 168829 X 31; 4, 2 + 0. 00847208 X 32; 3, 2 – 0. 0814444 X 32; 4, 2 – 0. 0516998 X 32; 5, 2 + 0. 0572467 X 33; 3, 3 – 0. 0907433 X 33; 3, 4 – 0. 0607952 X 33; 4, 3 – 0. 000423563 X 33; 4, 4 – 0. 0371152 X 33; 5, 3 – 0. 035384 X 33; 5, 4 – 0. 210923 Y 01; 1 – 0. 183784 Y 01; 2 + 0. 0602733 Y 02; 1 + 0. 0665762 Y 02; 2 + 0. 108243 Y 03; 1 + 0. 0886606 Y 11; 3 + 0. 0929961 Y 11; 4 + 0. 0195858 Y 11; 5 – 0. 198283 Y 12; 3 – 0. 202142 Y 12; 4 – 0. 331363 Y 13; 2 – 0. 0719458 Z 0; 1, 1, 1 + 0. 0321013 Z 0; 1, 2, 1 + 0. 0215768 Z 0; 2, 1, 1 – 0. 0680832 Z 0; 2, 2, 1 + 0. 0272048 Z 1; 1, 1, 2 + 0. 030143 Z 1; 1, 2, 2 + 0. 100317 Z 1; 2, 1, 2 – 0. 0710925 Z 1; 2, 2, 2 + 0. 0345458 Z 2; 1, 3, 1 + 0. 0405706 Z 2; 1, 4, 1 – 0. 0706414 Z 2; 2, 3, 1 + 0. 0458567 Z 2; 2, 4, 1 – 0. 0890676 Z 3; 1, 3, 2 – 0. 079818 Z 3; 1, 4, 2 + 0. 00383163 Z 3; 2, 3, 2 – 0. 0690593 Z 3; 2, 4, 2 – 0. 0318548 Z 4; 3, 1, 1 – 0. 0578945 Z 4; 3, 2, 1 – 0. 0370363 Z 4; 4, 1, 1 – 0. 0205342 Z 4; 4, 2, 1 – 0. 025263 Z 4; 5, 1, 1 – 0. 063479 Z 4; 5, 2, 1 – 0. 00379276 Z 5; 3, 1, 2 – 0. 0736296 Z 5; 3, 2, 2 + 0. 0115829 Z 5; 4, 1, 2 + 0. 0355973 Z 5; 4, 2, 2 – 0. 0187494 Z 5; 5, 1, 2 – 0. 0102523 Z 5; 5, 2, 2 – 0. 0985276 Z 6; 3, 3, 1 + 0. 0589642 Z 6; 3, 4, 1 + 0. 0673051 Z 6; 4, 3, 1 – 0. 0658495 Z 6; 4, 4, 1 – 0. 0111043 Z 6; 5, 3, 1 – 0. 03298 Z 6; 5, 4, 1 – 0. 128407 Z 7; 3, 3, 2 + 0. 0717031 Z 7; 3, 4, 2 + 0. 0659939 Z 7; 4, 3, 2 – 0. 018446 Z 7; 4, 4, 2 + 0. 0303057 Z 7; 5, 3, 2 + 0. 0681921 Z 7; 5, 4, 2.

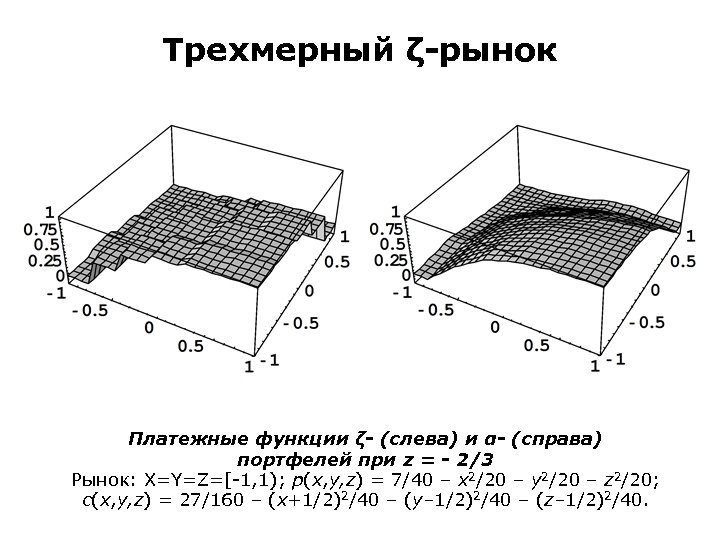Трехмерный ζ-рынок Платежные функции ζ- (слева) и α- (справа) портфелей при z = - 2/3 Рынок: X=Y=Z=[-1, 1); p(x, y, z) = 7/40 – x 2/20 – y 2/20 – z 2/20; c(x, y, z) = 27/160 – (x+1/2)2/40 – (y– 1/2)2/40 – (z– 1/2)2/40.

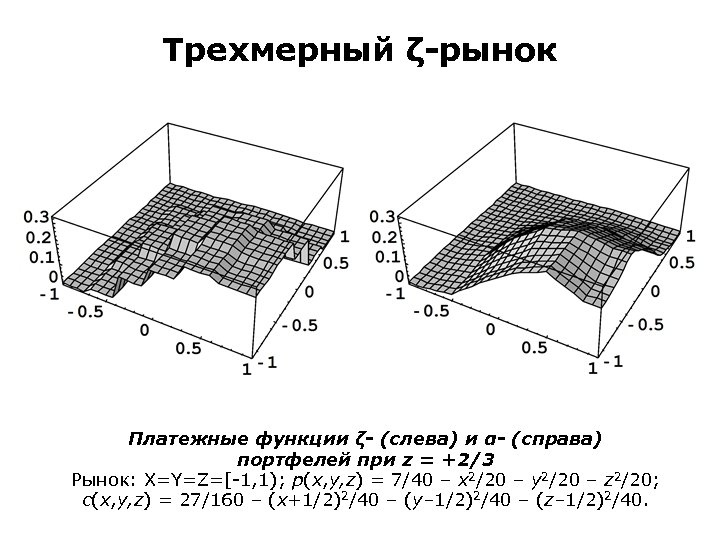Трехмерный ζ-рынок Платежные функции ζ- (слева) и α- (справа) портфелей при z = +2/3 Рынок: X=Y=Z=[-1, 1); p(x, y, z) = 7/40 – x 2/20 – y 2/20 – z 2/20; c(x, y, z) = 27/160 – (x+1/2)2/40 – (y– 1/2)2/40 – (z– 1/2)2/40.

Комбинированные рынки

Комбинированные рынки Пример 1. X=Y=[– 1, 1]; x X, y Y; n 1=20, n 2=15; p(x, y) = 13/36 – x 2/6 – y 2/6; c(x, y) = 37/120 – (x+1/2)2/20 – (y– 1/2)2/20. Платежные функции сценарных 2 d- и 1 dτ-портфелей (слева и справа соответственно)

Комбинированные рынки Платежные функции сценарных (2, 1)d-портфелей, построенных по упрощенному (слева) и строгому (справа) методам соответственно

Комбинированные рынки Пример 2. X=Y=[– 1, 1]; x X, y Y; n 1=20, n 2=15; p(x, y) = 3/10 – 3(x–y)2/40; c(x, y) = 29/100 – 3(x+y)2/50. Платежные функции сценарных 2 d- и 1 dτ-портфелей (слева и справа соответственно)

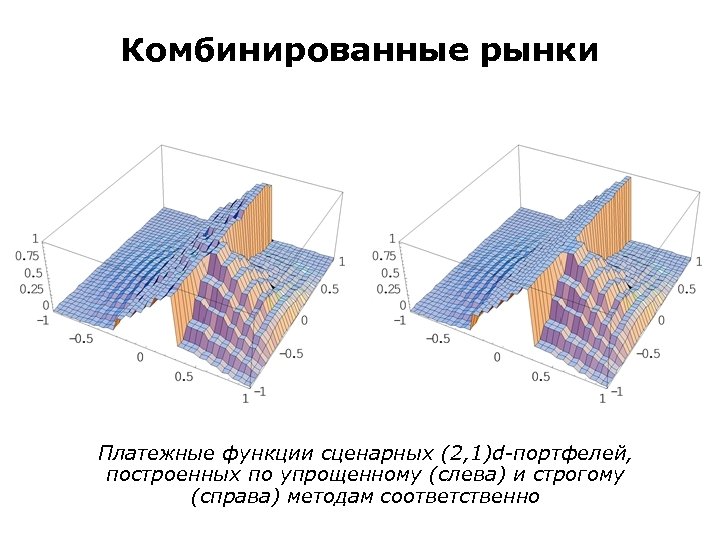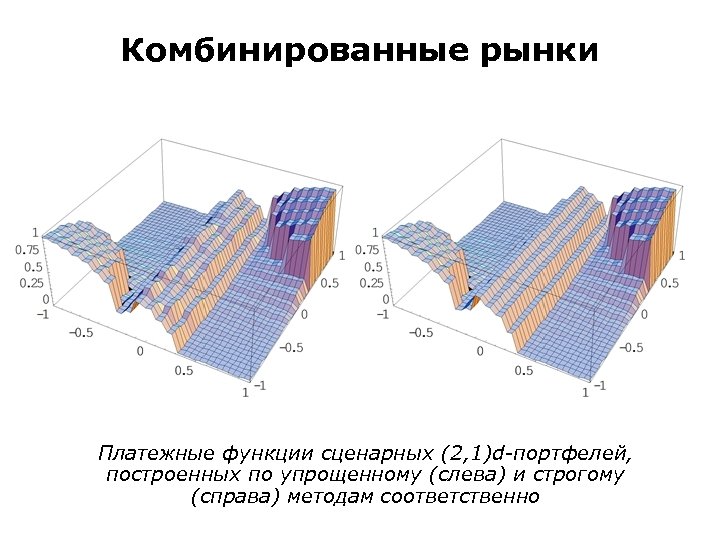Комбинированные рынки Таблица значений A, R, y для релевантных портфелей Пример 1. τ=0. 87; {0, 0, 1, 1, 1, 0, 0, 0, 0} • 2 -dim: {0. 273791, 0. 335295, 0. 224638} • 1 -dim: {0. 318633, 0. 361624, 0. 134922} • 1 -dim (rx): {0. 277211, 0. 361624, 0. 304508} • (2, 1) simplified: {0. 262105, 0. 335284, 0. 279199} • (2, 1) rigorous: {0. 273995, 0. 350872, 0. 280574} Пример 2. τ=0. 75; {0, 0, 1, 1, 1, 0, 0, 0, 0} • 2 -dim: {0. 239719, 0. 335227, 0. 398416} • 1 -dim: {0. 35538, 0. 360141, 0. 0133969} • 1 -dim (rx): {0. 266535, 0. 360141, 0. 351196} • (2, 1) simplified: {0. 219755, 0. 335211, 0. 525386} • (2, 1) rigorous: {0. 227555, 0. 34579, 0. 519586}

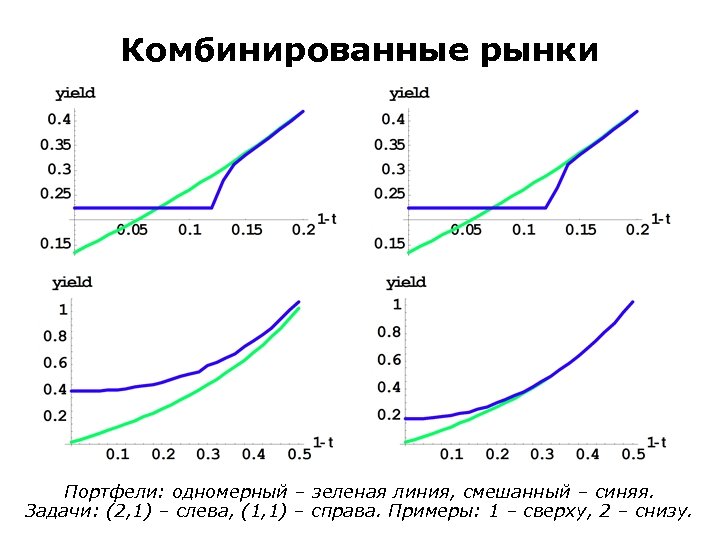Комбинированные рынки Портфели: одномерный – зеленая линия, смешанный – синяя. Задачи: (2, 1) – слева, (1, 1) – справа. Примеры: 1 – сверху, 2 – снизу.

Комбинированные рынки Сравнение рисунков с предыдущего слайда обнаруживает большее расхождение не по задачам ((2, 1)d и (1, 1)d), а по примерам рынков. В каждом примере графики для обеих задач качественно весьма похожи друг на друга. Расхождения, если они и есть, носят количественный характер. Меньшее значение доходности для (1, 1)d- по сравнению с (2, 1)d‑рынком в примере 2 в сравнении с примером 2′ обусловлено тем, что независимое задание цен смягчает противопоставление прогнозной и ценовой плотностей, свойственное примеру 2. В примере 1′ существует такое критическое значение τcr (0. 92, 0. 93), что при всех τ < τcr предпочтительны портфели из базисных инструментов исключительно одномерного рынка; при этом для τ > τcr предпочтительны портфели из базисных инструментов исключительно двумерного рынка (без "примеси" инструментария собственно одномерного рынка). В примере 2′ при всех значениях τ оказываются предпочтительными портфели из базисных инструментов комбинированного двумерного (реального или виртуализованного) и одномерного рынков.

Многопериодный рынок Предполагается, что на n-периодном рынке обращаются зависящие от траектории опционы (path-dependent options). Их платежные функции определяются в общем случае всей траекторией движения цены базового актива. Пусть x = (x 1, x 2, …, xn) и ς = (ς1, ς2, …, ςn) – векторы соответственно цен базового актива xi и страйков ςi , i I={1, 2…, n}, α = (α 1, α 2, …, αn) – набор чисел – 1 и +1 в любом порядке, характеризующий тип опциона. Среди всех зависящих от траектории опционов выделяются α-опционы A(ς; α) с платежной функцией a(x; ς; α) = ∏i Imax(0, αi(xi–ςi)). В соответствии с определением их свойства заимствуются у однопериодных многомерных α-опционов. • По существу, лучше было бы оперировать не самими ценами актива, а его разностными (xi–xi– 1) или относительными (xi/xi– 1) ценами (в зависимости от ставок) с включением x 0. • Необязательно требовать присутствия на рынке всех 2 n α-опционов для каждого ς n. Как и в однопериодном случае, достаточно, чтобы множество страйков, для которых определен хотя бы один тип -опциона, совпадало с n.

Многопериодный рынок Рынок многопериодных δ-инструментов

Многопериодный рынок Рынок многопериодных α-опционов

Трехпериодный рынок Пример (заимствуется из однопериодного трехмерного рынка). Формирование данных X=Y=Z=[– 1, 1); x X, y Y, z Z – последовательные цены. Задаются прогнозная и нормированная ценовая плотности: p(x, y, z) = 7/40 – x 2/20 – y 2/20 – z 2/20; c*(x, y, z) = 27/160 – (x+1/2)2/40 – (y– 1/2)2/40 – (z– 1/2)2/40; p(x) = (17– 6 x 2)/30 = y Y, z Z p(x, y, z) dy dz; c*(x) = (16– 3 x 2)/30 = y Y, z Z c*(x, y, z) dy dz; p(x, y) = (19– 6 x 2– 6 y 2)/60 = z Z p(x, y, z) dz; c*(x, y) = (17 – 3 x(1+x) + 3 y(1–y))/60 = z Z c*(x, y, z) dz. r = r 03 – средний относительный доход за весь трехпериодный горизонт инвестирования (>1); r 01, r 02 – средние относительные доходы за первый и первые два периода инвестирования соответственно. Эти параметры задаются произвольно; с помощью них задаются реальные (не нормированные) ценовые плотности, которые, вообще говоря, уже не вероятностные: c(x, y, z) = c*(x, y, z)/r 03; c(x) = c*(x)/r 01; c(x, y) = c*(x, y)/r 02; при этом портфель остается прежним, а меняются лишь A и y.

Трехпериодный рынок Пример. Оптимальный портфель в терминах -опционов C и опционов CXY, CXZ, CYZ, CX, CY, CZ. G = i, j, k gijk. B[i, j, k] = 0. 0783594 U+0. 652028 C[1, 1, 1]– 0. 328364 C[1, 1, 2]– 0. 323664 C[1, 1, 3]– 1. 10107 C[1, 2, 1]+1. 44477 C[1, 2, 2]– 0. 343699 C[1, 2, 3]+0. 82855 C[1, 3, 1]– 0. 620154 C[1, 3, 2]– 0. 208396 C[1, 3, 3]+0. 148284 C[1, 4, 1]– 0. 123879 C[1, 4, 2]– 0. 0244049 C[1, 4, 3]– 0. 527796 C[1, 5, 1]– 0. 372368 C[1, 5, 2]+0. 900163 C[1, 5, 3]– 0. 0767373 C[2, 1, 1]+0. 62022 C[2, 1, 2]– 0. 543483 C[2, 1, 3]+0. 708291 C[2, 2, 1]– 2. 3426 C[2, 2, 2]+1. 6343 C[2, 2, 3]– 1. 51307 C[2, 3, 1]+1. 51614 C[2, 3, 2]– 0. 00307589 C[2, 3, 3]+0. 647775 C[2, 4, 1]+0. 365485 C[2, 4, 2]– 1. 01326 C[2, 4, 3]+0. 233736 C[2, 5, 1]– 0. 15925 C[2, 5, 2]– 0. 0744859 C[2, 5, 3]– 1. 38698 C[3, 1, 1]+0. 769723 C[3, 1, 2]+ 0. 617259 C[3, 1, 3]+1. 83324 C[3, 2, 1]– 1. 24058 C[3, 2, 2]– 0. 592661 C[3, 2, 3]+0. 140683 C[3, 3, 1]– 0. 368137 C[3, 3, 2]+ 0. 227454 C[3, 3, 3]– 1. 06554 C[3, 4, 1]+1. 05961 C[3, 4, 2]+ 0. 00592486 C[3, 4, 3]+0. 478598 C[3, 5, 1]– 0. 220621 C[3, 5, 2]– 0. 257976 C[3, 5, 3]+0. 582709 C[4, 1, 1]– 0. 941666 C[4, 1, 2]+ 0. 358957 C[4, 1, 3]– 2. 19114 C[4, 2, 1]+3. 45283 C[4, 2, 2] – 1. 2617 C[4, 2, 3]+2. 02687 C[4, 3, 1]– 2. 44481 C[4, 3, 2] + 0. 417943 …

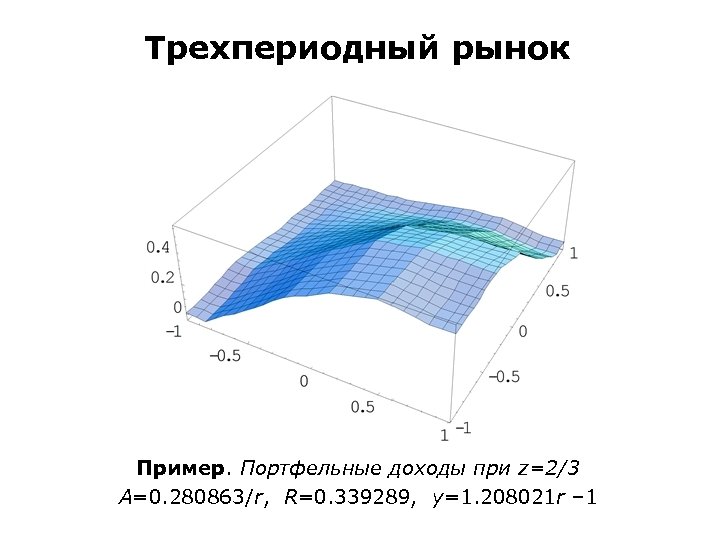Трехпериодный рынок Пример. Портфельные доходы при z=2/3 A=0. 280863/r, R=0. 339289, y=1. 208021 r – 1

Принцип минимума доходности Свойство 1. Если для некоторого выполняется ( ; ) ( ; ), для всех [0, 1], , то для любой монотонно возрастающей и ограниченной функции ( ) имеет место = min. Свойство 2. Если задаче 1 = ( (x), (x)), где c, p, соответствует функция ( ), то двойственной задаче 2 = ( (x), (x)) соответствует функция *( )=1– (– 1)(1– ), [0, 1]. Свойство 3. Пусть функции 1( ) и 2( ) на отрезке [0, 1] строго монотонно возрастают и не претерпевают скачков, причем 1( ) 2( ), а 1*( ) и 2*( ) – функции, получающиеся из 1( ) и 2( ) соответственно из свойства 2. Тогда и 1*( ) 2*( ), [0, 1]. Свойство 4. Пусть семейства { 1( ; ), 1} и { 2( ; ), 1} порождены задачами 1( ) = {( (x), (x– ), 1)} и 2( ) = = {( (x), (x– )), 1} соответственно и у первого семейства существует минимальный элемент 1( ; 1). Тогда функция 2*( ; 2) = 1– 1(– 1)(1– ; 1), 2 = – 1, является минимальным элементом второго семейства.

Принцип минимума доходности Свойство 5†. Функция ( ) в задаче = ( (x), (x)) с плотностями, множества нулей которых имеют нулевую меру Лебега, строго вогнута. Свойство 6†. Пусть p = P { (x)>0, (x)=0}, p = P { (x)=0, (x)>0}. Тогда функция ( ) в задаче = ( (x), (x)) имеет скачок в нуле величиной p и принимает постоянное значение, равное 1, на отрезке [1–p , 1] длины p. На (0, 1–p ) функция ( ) строго возрастает и вогнута (ее производная строго убывает). Свойство 7†. Пусть p = P { (x)>0, (x)=0}, p = P { (x)=0, (x)>0}. Тогда функция ( ) в задаче = ( (x), (x)) не может иметь скачков кроме точки =0 и участков постоянства при ( ) 1. ■ Приведенные утверждения можно с некоторыми оговорками и уточнениями распространить и на дискретные распределения, и на комбинации дискретных и непрерывных распределений. Проверять принцип можно и на однопараметрических семействах распределения (Парето, полунормальное и пр. ). В его пользу будет говорить равенство min = * (значение параметра для ценовой плотности) и, стало быть, тождество p(x, min) ≡ c(x, *). † См. также разд. ″Процедура Неймана-Пирсона″.

Принцип минимума доходности Примеры [{ , }, c, p; ( )= ] Определение оптимального среднего Пример 1. (x) = ½exp(–|x|), (x) = ½exp(–|x– |/ )/ , x , <1, = . Решение. : min = 0 ( ; min) ( ; ). Пример 2. (x)=½exp(–|x|), (x)=½( (x– +s)+ (x– –s)), x , s>0, = . Решение. s > ln(2 +1– 1): min = s; s < ln(2 +1– 1): min = 0. Определение оптимального разброса Пример 3. (x) = R(0, 2), (x) = R( , 2 s), x , , =s>0. Решение. cr: (1– )(1+ ) =1; ( , | >1 <1 & < cr): smin=1+ ; ow: smin=1–. Пример 4. (x) – непрерывная симметричная плотность на отрезке [ – 1, 1], (i) вогнутая на интервале (– 1, 1) или (ii) выпуклая на интервалах (– 1, 0) и (0, 1); (x) = ½( (x– +s)+ (x– –s)), x , , =s>0. Решение. >1: smin= ; ( | ½< 1): (i) smin=0, (2 )> (0); smin= , (2 )< (0); (ii) smin=1– , (2 – 1)+ (1)> (0); smin= , (2 – 1)+ (1)< (0); ( | 0< ½): (i) smin=0, (ii) smin=.

Принцип минимума доходности Примеры – общая дискретно-континуальная задача p( ), c, ρ( ) = (ρ1, ρ2, …, ρn), ρj = pj( )/cj, – вектор относительных доходов; ( ; ) = i– 1 + i( )( – i– 1( )), i– 1( )< ≤ i( ), 0( )=0, i I (в предположении C 1). Пример 5. c ≡ (1/6, 1/2, 1/3), p ≡ (3/4– , 1/4, ), 0≤ ≤ 3/4. Решение. min = argmin ( ; ) = 1/2, p( min) = (1/4, 1/2). Пример 6. c ≡ (1/2, 0), p ≡ ( , 1– 2 , ), 0≤ ≤ 1/2; минимальной функции ( ; min) не существует. Варианты: (1) ( ) ≡ 1+ , 0. Решение. : min = 1/3; p( min)=(1/3, 1/3). (2) ( ) ≡ {1– + , 0≤ ≤ 1; {0, ≤ 1– 1/ ; – +1, >1– 1/ }, >1}. Решение. cr=3– 31/2 1. 27. > cr: min = 0; p( min)=(0, 1, 0); < cr: min = 1/3; p( min)=(1/3, 1/3); . (3) ( ) ≡ . Решение. cr=ln 2/(ln 3–ln 2) 1. 71. > cr: min = 0; p( min)=(0, 1, 0); < cr: min = 1/3; p( min)=(1/3, 1/3).

Переформирование портфеля m – коэффициент, показывающий, какому количеству базовых акций соответствует один опцион (например 100); – признак короткой позиции по базовому активу, т. е. = 1 для короткой позиции и = 0 – для длинной; C 0 – суммарные денежные средства на момент переформирования портфеля на маржевом счете и счете до востребования; D 0 – суммарная денежная задолженность инвестора перед брокером к моменту переформирования портфеля (возникает при покупке базового актива по маржевому счету); Ds 0 – задолженность инвестора перед брокером в акциях к моменту переформирования портфеля (возникает при короткой продаже базового актива); A – портфель инвестора перед переформированием портфеля; f – комиссионные (f. I, f. T, f. F – комиссионные при создании новой позиции, трансформации портфеля и ликвидации позиции соответственно), f 0 – вектор "удельных" комиссионных расходов для компонент портфеля; n 0, n 1, …, nk – количества инструментов в портфеле; индекс "0" соответствует базовому активу в портфеле, остальные – опционам; pm = (p 0, p 1, …, pk) – вектор рыночных цен всех инструментов из портфеля, средних между ценами покупателя и продавца; = ( 0, 1, …, k) – вектор спредов цен продавца и покупателя; U – единичный портфель, тестируемый инвестором для переформирования портфеля (например покрытая продажа колла);

Переформирование портфеля B – портфель инвестора, получающийся в результате переформирования портфеля (B' – первая, грубая, оценка); Eq – собственные средства в портфеле на маржевом счете при покупке базового актива по маржевому счету; Eq = 0 для короткой позиции по базовому активу; Ed – депозит денежных средств на маржевом счете при короткой продаже базового актива по маржевому счету; Ed = 0 для длинной позиции по базовому активу; Mis(N), Mio(N), Mi(N) = Mis(N) + Mio(N) – начальная маржа соответственно для базового актива портфеля N, опционной части портфеля в целом (расходуется на покупку базового актива или служит обеспечением при короткой продаже и является чистым инвестиционным расходом); Mis(N) = Eq + Ed; R – денежные средства, выделяемые инвестором в качестве резерва и откладываемые на счете до востребования для обеспечения возможных предстоящих выплат вариационной маржи брокеру на интервале инвестирования для поддержания позиции; D 1 – денежная задолженность инвестора перед брокером непосредственно после переформирования портфеля (возникает при покупке базового актива по маржевому счету); Ds 1 – задолженность инвестора перед брокером в акциях непосредственно после переформирования (возникает при короткой продаже базового актива);

Переформирование портфеля T = T(A, B) – стоимость преобразования портфеля A в портфель B (деньги, потраченные на приобретение новых инструментов, за вычетом денег, полученных от продажи ненужных старых инструментов, плюс комиссионные), Ts(N), To(N), T(N) – стоимости построения с "нуля" фондовой части портфеля N, его опционной части и портфеля в целом соответственно. S – денежные средства, получаемые при короткой продаже базовых акций, которые инвестор заимствует у брокера; эту сумму инвестор должен держать на маржевом счете до погашения акций (задолженности Ds 1); для коротких акций S = –Ts(B); In = Mi(N; p) + To(N) + f – чистая начальная инвестиционная сумма с резервом при построении портфеля N "с нуля" (используется при расчете доходности трансформации портфеля); If = In + R – чистая начальная инвестиция, дополненная резервной суммой; C 1 = C 0 – D 0 + D 1 – T(A, B) – суммарные денежные средства на обоих счетах инвестора сразу после переформирования портфеля; Cm = – Ts(B) + Mis + Mio – необходимые денежные средства на маржевом счете сразу после переформирования портфеля; Cd = C 1 – Cm – денежные средства, которые сразу после трансформации портфеля можно направить на счет до востребования; C 1 = Cd – R – возникающие при переформировании портфеля излишки денежных средств, которых недостаточно, чтобы приобрести целый единичный портфель (балансовое соотношение);

Переформирование портфеля Cn – суммарные денежные средства на обоих счетах на конец интервала инвестирования без учета вариационной маржи; Следующие обозначения используются при оценивании доходности целевого портфеля. Заданные извне параметры: – длина интервала инвестирования в годах; rm – маржевая процентная ставка; rd – безрисковая процентная ставка по счету до востребования; d – дивиденды, выплачиваемые инвестором брокеру при короткой продаже акций (d > 0) или получаемые на акции при их покупке (d < 0) на интервале инвестирования. Переменные, определяемые на конец интервала инвестирования в зависимости от цены x базового актива: x – цена базового актива в конце интервала инвестирования; Eq(x) – собственные средства в портфеле на маржевом счете при цене x базового актива (требование возникает при покупке базового актива по маржевому счету); Eq(x) = 0 для короткой позиции по базовому активу; Ed(x) – размер необходимого депозита денежных средств на маржевом счете при цене x базового актива (требование возникает при короткой продаже базового актива по маржевому счету); Ed(x) = 0 для длинной позиции по базовому активу; Mm(x) – поддерживающая маржа;

Переформирование портфеля a(x) ( 0), b(x) ( 0) – объемы денежных средств, которые инвестор должен вносить на маржевый счет и может изымать с маржевого счета соответственно; a(x) и b(x) не могут быть положительными одновременно; Mvs(x), Mvo(x), Mv(x) = Mvs(x) + Mvo(x) – вариационная маржа соответственно для базовых акций, опционной составляющей портфеля и портфеля в целом; также Mv(x) = a(x) – b(x); Isvm(x), Iovm(x), Ivm(x) = Isvm(x) + Iovm(x) – интегральные оценки на интервале инвестирования чистого инвестиционного расхода (с учетом временной стоимости денег), обусловленного вариационной маржей, соответственно для фондовой, опционной частей портфеля и портфеля в целом; Q = m. Ivm(x) – эффективная (приведенная к началу временного интервала) оценка объема денежных средств, которые на рассматриваемом интервале инвестирования переводятся со счета до востребования на маржевый счет (при Q > 0) или обратно (при Q < 0) для погашения требований брокера по вариационной марже; PB(x) – платежная функция портфеля B; F(x) = Cn + PB(x) – Q(x)rd – капитал инвестора на конец интервала инвестирования; Y(x) = (F(x) – Km)/(Km ) – доходность трансформации портфеля за интервал инвестирования в годовом выражении.

Переформирование портфеля Динамика маржевого счета для базового актива Начальная маржа для длинной и короткой позиций задается соответственно параметрами μl < 1 и μs < 1, а поддерживающая – μml μl и μms μs; p – начальная цена базового актива, x – конечная. Длинная позиция. Mis = Eq = μlp, M = 0, D = p – Eq = (1–μl)p, Eq(x) = x – (1–μl)p; Eq(x) μmlx, a(x) = max[μmlx–Eq(x), 0] = max[(1–μl)p–(1–μml)x, 0]; Eq(x) μlx, b(x) = max[Eq(x)–μlx, 0] = max[(1–μl)(x–p), 0]; p(1–μl)/(1–μml) < x < p status quo, Mv(x) = a(x) – b(x). Короткая позиция. Mis = Ed = μsp, M = (1+μs)p, D = 0, Ed(x) = (1+μs)p – x; Ed(x) μmsx; a(x) = max[μmsx–Ed(x), 0] = max[(1+μms)x–(1+μs)p, 0]; Ed(x) μsx; b(x) = max[Ed(x)–μsx, 0] = max[(1+μs)(p–x), 0]; p < x < p(1+μs)/(1+μms) status quo, Mv(x) = a(x) – b(x).

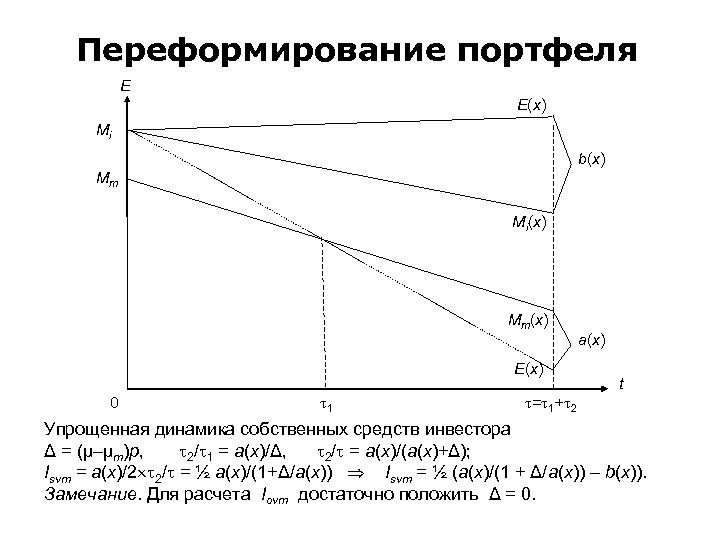Переформирование портфеля E E(x) Mi b(x) Mm Mi(x) Mm(x) E(x) 0 1 a(x) t = 1+ 2 Упрощенная динамика собственных средств инвестора Δ = (μ–μm)p, 2/ 1 = a(x)/Δ, 2/ = a(x)/(a(x)+Δ); Isvm = a(x)/2 2/ = ½ a(x)/(1+Δ/a(x)) Isvm = ½ (a(x)/(1 + Δ/a(x)) – b(x)). Замечание. Для расчета Iovm достаточно положить Δ = 0.

Переформирование портфеля A – портфель инвестора в текущий момент времени. Он состоит из нескольких лотов (по m = 100) акций и нескольких опционов колл и пут на эту акцию (каждый опцион на m акций). Изучается целесообразность перехода от A к портфелю B = q U где U – единичный портфель заданного типа, а q – целое число. Вариационная маржа на момент трансформации позиции неизвестна и моделируется случайной величиной, зависящей от будущей цены базового актива. Для решения этой проблемы создается резерв на счете до востребования. N = (n 0, n 1, …, nk) – портфель с n 0 лотами акций и ni опционами i-го класса, i I = {1, 2, …, k}; p = (p 0, p 1, …, pk) – совокупность рыночных цен всех инструментов из портфеля, средних между ценами покупателя и продавца; = ( 0, 1, …, k), где i (>0) – спред цен для i-го инструмента; vm(N) – средняя стоимость портфеля N, s(N) – спред цен портфеля N; vl(N) – нижняя стоимость, получается при ликвидации портфеля по худшим для инвестора ценам; vm(N) = inipi, s(N) = i|ni|δi, vl(N) = vm(N)– 0. 5 s(N); f = (|N|, f 0), где f 0 – вектор удельных комиссионных для компонент портфеля.

Переформирование портфеля Шаг 1 находит величину резерва RU, необходимого для покрытия требований брокера по вариационной марже для U с вероятностью . Решается задача: Пусть цена актива x = LN( , ), yi = (ln(xi)– )/ – i-квантиль для N(0, 1), i = 1, 2. Найти пару (x 1, x 2), такую что 2– 1 = и RU min. Шаг 2 оценивает располагаемый на текущий момент времени капитал инвестора. Оценки капитала Km = C 0 – D 0 + mvm(A), Kl = C 0 – D 0 + mvl(A) = Km – 0. 5 ms(A). Шаг 3 определяет объем чистой начальной инвестиции In для построения портфеля U по худшим ценам, и сумму этой же инвестиции, но вместе с резервом: If = In + RU. Шаг 4 находит портфель B' = q' U, q' – целое положительное число, который можно построить исходя из капитала Kl, q' = [Kl/(m. If)], и объем остаточных денежных средств ' = Kl – q'm. If. Шаг 5 проводит одну итерацию располагаемого капитала с учетом сохранения части портфеля A. Количество любого инструмента в общей части G портфелей A и B' находится по правилу: ng = {0, nanb 0; sign[na]min[|na|, |nb|], nanb>0}, где na и nb – его количества в портфелях A и B' соответственно (иначе, ng = Median{0, na, nb}). Сохранение G из портфеля A для использования в портфеле B' сэкономит сумму = (|G|, δ). Поэтому K = Kl + m.

Переформирование портфеля Шаг 6 проводит коррекцию полученного портфеля с учетом нового располагаемого капитала K (повторяет шаг 4). Имеем q = [K/(m. If)], B = q U, = K – qm. If. Шаг 7 находит объем чистой начальной инвестиции (повторяет шаг 3) для портфеля B. Для него определяется и значение резерва: R = q. Ru. Шаг 8 осуществляет фактическую трансформацию портфеля, т. е. определяет, что купить, что продать и сколько это будет стоить. Для портфеля N = A – B находятся его средняя стоимость vm( N) и суммарный спред цен s( N), а также рассчитываются комиссионные f. T. По ним с использованием худших для инвестора цен стоимость трансформации портфеля T(A, B) = vm( N) + s( N)/2 + f. T, где f. T = (| N|, f 0). Шаг 9 определяет состояние денежных средств на обоих счетах непосредственно после трансформации портфеля. Суммарный объем денежных средств на обоих счетах C 1 = C 0 – D 0 + D 1 – T(A, B). Денежные средства на маржевом счете, включая сумму S = –Ts(B) в случае короткой позиции по акциям, Cm = S + Mis(B) + Mio(B) ( = 1 для короткой позиции, = 0 – для длинной). Денежные средства на счете до востребования Cd = C 1 – Cm. Суммарный остаток денежных средств на счетах C 1 = C 1 – Cm – m. R (он, как правило, положителен).

Переформирование портфеля Шаг 10 дает оценку среднего капитала инвестора в конце периода и рассчитывает доходность трансформации. Средний капитал F(x) зависит от будущей цены x базового актива. В расчете используются средние цены между ценами покупателя и продавца. F(x) = PB(x) + Cn – Q(x)rd ; PB(x) = n 0 x + i=1, . . . , k (nci max[0, x – ei] + npi max[0, ei –x]); Cn = C 1 – D 1(1+rm ) – md – mf. F + Cdrd ; Q(x) = m. Ivm(x), где Ivm(x) – часть чистого инвестиционного расхода, обусловленная вариационной маржей и зависящая от вида строящегося портфеля; Y(x) = (F(x) – Km)/(Km ). Замечание. Поскольку значение располагаемого капитала варьируется в пределах от Km – 0. 5 ms(A) до Km + 0. 5 ms(A), относительная ошибка в определении доходности инвестиции за счет выбора Km не превысит ms(A)/(2 Km ). При сравнительном анализе всех вариантов переформирования ошибка в определении "наилучшего" целевого портфеля будет еще меньше. Учет фактора времени в последней формуле обязателен, когда сравниваются инвестиции в два портфеля, вообще говоря, с различными временными горизонтами.

Переформирование портфеля Иллюстративные примеры: (1) покрытая продажа колла, (2) покрытая продажа пута В первом из них портфель "покрытая продажа колла" трансформируется в портфель того же типа, но с бóльшим страйком у колла, а во втором – аналогичная операция проводится уже с портфелем "покрытая продажа пута". В первом примере осуществляется покупка базовой акции, а во втором – ее короткая продажа. Общие данные: μl = μs = 0. 5, μml = μms = 0. 25, длительность года y = 365. 25, процентная ставка по брокерскому кредиту rm = 0. 1 (10%), ставка до востребования rd = 0. 05 (5%), время до истечения срока опционов 91 день, или = 0. 249144 года. Прогноз цены базовой акции – логнормальная случайная величина. Ее параметры: волатильность в годовом выражении = 0. 3, средняя будущая цена p 0 = 53. 0 (равна текущей). Цены покупателя и продавца также логнормальны. Их средние соответственно равны p 0” = p 0 + 0/2 = 53. 8 и p 0’ = p 0 – 0/2 = 52. 2, а волатильности совпадают с . Все комиссионные равны нулю, равно как и дивиденды на рассматриваемом интервале времени.

Переформирование портфеля Пример. Покрытая продажа колла A = qo{1, – 1, 0}, qo = 37; компоненты портфеля с i=1, 2 отвечают опционам колл со страйками e 1 = 50, e 2 = 55; цены продавца и покупателя задаются векторами pm = {53. 0, 5. 0, 2. 0} и δ = 2 {0. 8, 0. 3, 0. 1}; C 0 = 55000, D 0 = 100000, Ds 0 = 0. A q U, U = {1, 0, – 1}. Шаги: #1. = 0. 9; {p 0” = 53. 8, = 0. 3} { = 3. 95673, = 0. 164717} { 1 = 0. 0 (с высокой точностью), 2 = 0. 9, x 1 = 23. 3471, x 2 = 64. 4549} Ru = 9. 45488. #2. s(A) = 81. 4, Km = 132600. 0, Kl = 128530. 0. #3. Ts = nsp 0” = 53. 8, Mis = Eq = μl. Ts = 26. 9, D 1 = Ts – Eq = 26. 9; To = no(p 2 – 2/2)= – 1. 9, Mio = nomax[p 0” – e 2, 0] = 0. 0; Mi = Mis + Mio = 26. 9; In = Mi + To = 25. 0; If = In + Ru = 34. 4549. #4. q' = [Kl/(m. If)] = 37, B' = q' U = q' {1, 0, – 1} = {37, 0, – 37}, ' = Kl – q'm. If = 1046. 93. #5. A B' ={37, 0, 0}; = 59. 2, K = 134450. 0. #6. q = [K/(m. If)] = 39; B = q U = q {1, 0, – 1} = {39, 0, – 39}; = K – qm. If = 75. 9547. #7. Ts = 2098. 2, Mis = Eq = μl. Ts = 1049. 1, D 1 = 1049. 1; To = – 74. 1, Mio = 0. 0, Mi = 1049. 1, In = 975. 0; R = q. Ru = 368. 74. #8. N = A – B = {2, 37, – 39}; T = vm( N) = ( N, pm) + (| N|, δ)/2 + f. T = 229. 6.

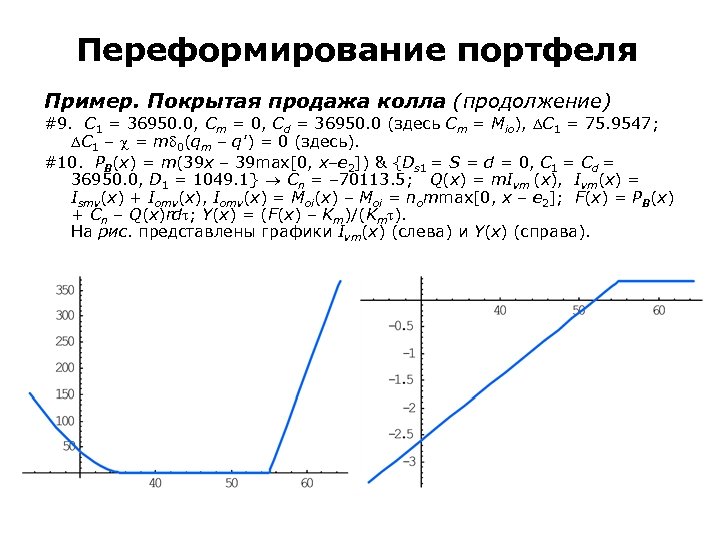Переформирование портфеля Пример. Покрытая продажа колла (продолжение) #9. C 1 = 36950. 0, Cm = 0, Cd = 36950. 0 (здесь Cm = Mio), C 1 = 75. 9547; C 1 – = m 0(qm – q') = 0 (здесь). #10. PB(x) = m(39 x – 39 max[0, x–e 2]) & {Ds 1 = S = d = 0, C 1 = Cd = 36950. 0, D 1 = 1049. 1} Cn = – 70113. 5; Q(x) = m. Ivm (x), Ivm(x) = Ismv(x) + Iomv(x), Iomv(x) = Moi(x) – Moi = nommax[0, x – e 2]; F(x) = PB(x) + Cn – Q(x)rd ; Y(x) = (F(x) – Km)/(Km ). На рис. представлены графики Ivm(x) (слева) и Y(x) (справа).

Переформирование портфеля Пример. Покрытая продажа пута A = qo{– 1, 0}, qo = 37; компоненты портфеля с i=1, 2 отвечают опционам пут со страйками e 1 = 50, e 2 = 55; цены продавца и покупателя задаются векторами pm = {53. 0, 1. 0, 4. 0} и δ = 2 {0. 8, 0. 1, 0. 25}; C = 321000, D = 0, Ds = – 37. A q U, U = {– 1, 0, – 1}. Шаги: #1. = 0. 9; {p 0’ = 52. 2, = 0. 3} { = 3. 94387, = 0. 149743} { 1 = 0. 0 (с высокой точностью), 2 = 0. 9, x 1 = 42. 202, x 2 = 72. 8553} Ru = 9. 99805. #2. s(A) = 66. 6, Km = 121200. 0, Kl = 117870. 0. #3. Ts = ns p 0’ = – 52. 2, Mis = Ed = –μl. Ts = 26. 1, D 1 = 0. 0; To = no(p 2 – 2/2) = – 3. 75, Mio = nomax[e 2 – p 0’, 0] = 2. 8; Mi = Mis + Mio = 28. 9; In = Mi + To = 25. 15; If = In + Ru = 35. 148. #4. q' = [Kl/(m. If)] = 33, B' = q' U = q' {– 1, 0, – 1} = {– 33, 0, – 33}, ' = Kl – q'm. If = 1881. 45. #5. A B' = {– 33, 0, 0}; = 52. 8, K = 123150. 0. #6. q = [K/(m. If)] = 35; B = q U = q {– 1, 0, – 1} = {– 35, 0, – 35}; = K – qm. If = 131. 838. #7. Ts = – 1827. 0, Mis = Ed = –μl. Ts = 913. 5, D 1 = 0. 0; To = – 131. 25, Mio = 98. 0, Mi = 1011. 5, In = 880. 25; R = q. Ru = 349. 932. #8. N = A – B = {2, 37, – 35}; T = vm( N) = ( N, pm) + (| N|, δ)/2 + f. T = 17. 05.

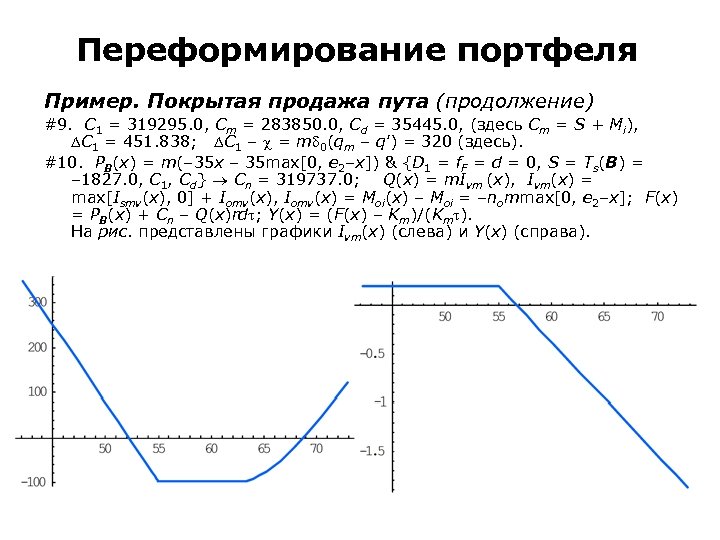Переформирование портфеля Пример. Покрытая продажа пута (продолжение) #9. C 1 = 319295. 0, Cm = 283850. 0, Cd = 35445. 0, (здесь Cm = S + Mi), C 1 = 451. 838; C 1 – = m 0(qm – q') = 320 (здесь). #10. PB(x) = m(– 35 x – 35 max[0, e 2–x]) & {D 1 = f. F = d = 0, S = Ts(B) = – 1827. 0, C 1, Cd} Cn = 319737. 0; Q(x) = m. Ivm (x), Ivm(x) = max[Ismv(x), 0] + Iomv(x), Iomv(x) = Moi(x) – Moi = –nommax[0, e 2–x]; F(x) = PB(x) + Cn – Q(x)rd ; Y(x) = (F(x) – Km)/(Km ). На рис. представлены графики Ivm(x) (слева) и Y(x) (справа).

CC-Va. R: Литература 1. 2. 3. 4. 5. 6. 7. Агасандян Г. А. Финансовая инженерия и критерий допустимых потерь (Va. R). М. : ВЦ РАН, 2001. 34 с. Агасандян Г. А. Об оптимальном поведении инвестора на рынке опционов / Труды Международной научно-практической конференции "Теория активных систем – 2001". Москва, 19 -21 ноября 2001. Агасандян Г. А. Многоступенчатый критерий Va. R на реальном рынке опционов. М. : ВЦ РАН, 2002. 35 с. Agasandian G. A. Optimal Behavior of an Investor in Option Market / International Joint Conference on Neural Networks. The 2002 IEEE World Congress on Computational Intelligence. Honolulu, Hawaii, Mai 12 -17, 2002. P. 1859 -1864. Агасандян Г. А. Описание поведения инвестора на многопериодном рынке опционов. М. : ВЦ РАН, 2003. 29 с. Агасандян Г. А. Применение инвесторами методов финансовой инженерии на рынке опционов / Труды Третьей международной конференции "Современные сложные системы управления (СССУ/HTCS‘ 2003). " Воронеж, 26 -28 мая 2003. Агасандян Г. А. Принцип минимума дохода для инвестора рынка опционов. М. : ВЦ РАН, 2004. 51 с.

CC-Va. R: Литература 8. 9. 10. 11. 12. 13. Агасандян Г. А. Новый подход к управлению портфелем ценных бумаг / Труды Четвертой международной конференции "Современные сложные системы управления (СССУ / HTCS‘ 2004)". Тверь, 24 -25 мая 2004. С. 8 -10. Agasandian G. A. A portfolio management approach based on continuous Va. R-criterion / Труды 4 -й Московской международной конференции по исследованию операций (ORM 2004). Москва, Сентябрь, 21 -24, 2004. МАКС Пресс. С. 4 -9. Агасандян Г. А. Финансовая инженерия и континуальный критерий Va. R на рынке опционов // Экономика и математические методы, 2005. Т. 41, № 4. С. 88 -98. Агасандян Г. А. Спрэды и баттерфляи в оптимизации портфеля на рынке опционов / Труды Международной научнопрактической конференции "Теория активных систем – 2005". Москва, ИПУ РАН, 16 -18 ноября 2005. С. 170 -171. Агасандян Г. А. Многоступенчатый критерий Va. R на произвольном однопериодном рынке. М. : ВЦ РАН, 2005. 45 с. Агасандян Г. А. Принцип минимума относительного дохода на произвольном однопериодном рынке. М. : ВЦ РАН, 2006. 22 с.

CC-Va. R: Литература 14. Agasandian G. A. Some problems of using the multistage Va. Rapproach in real option markets / Труды 5 -й Московской международной конференции по Исследованию Операций (ORM 2007). Москва, 10 -14 апреля 2007. МАКС Пресс. С. 292 -293. 15. Агасандян Г. А. Особенности применения многоступенчатого критерия Va. R на опционных рынках. М. : ВЦ РАН, 2007. 31 с. 16. Агасандян Г. А. Проблема переформирования портфеля ценных бумаг при наличии маржевых требований / Труды Международной научно-практической конференции "Теория активных систем – 2007". Москва, 14 -15 ноября 2007. С. 100 -104. 17. Агасандян Г. А. О проблемах переформирования портфеля на опционных рынках. М. : ВЦ РАН, 2008. 38 с. 18. Агасандян Г. А. Проблемы управления денежными средствами на опционном рынке / Труды Восьмой международной конференции "Современные сложные системы управления (СССУ / HTCS‘ 2008)". Тверь, 6 -7 мая 2008. Ч. 1. С. 7 -12.

CC-Va. R: Литература 19. Агасандян Г. А. Модификация континуального критерия Va. R для реального рынка опционов / Труды Восьмой международной конференции "Современные сложные системы управления (СССУ / HTCS‘ 2008)". Тверь, 6 -7 мая 2008. Ч. 2. С. 31 -35. 20. Агасандян Г. А. Континуальный критерий Va. R при использовании коротких позиций на рынке опционов / Материалы Второй международной конференции "Управление развитием крупномасштабных систем". ИПУ РАН, 1 -3 октября 2008. С. 189 -191. 21. Агасандян Г. А. Континуальный критерий Va. R – постановки задач и их решение. / Труды ИСА РАН "Динамика неоднородных систем". М. : ИСА РАН, 2008. Т. 39(1). С. 154 -165. 22. Агасандян Г. А. Об адаптации континуального критерия Va. R к дискретным рынкам. М. : ВЦ РАН, 2009. 42 с. 23. Агасандян Г. А. Основные теоретические схемы применения континуального критерия Va. R. М. : ВЦ РАН, 2009. 33 с.

CC-Va. R: Литература 24. Агасандян Г. А. Основные парадигмы использования континуальной параметризации риска на финансовых рынках / Материалы Третьей международной конференции "Управление развитием крупномасштабных систем". ИПУ РАН, 1 -3 октября 2009. С. 221 -223. 25. Агасандян Г. А. Анализ корректности семейств функций рисковых предпочтений / Труды Международной научнопрактической конференции "Теория активных систем – 2009". ИПУ РАН, 17 -19 ноября 2009. Т. 2. С. 161 -164. 26. Агасандян Г. А. Сравнительный анализ вариантов сценарного применения континуального критерия Va. R / Труды Международной научно-практической конференции "Теория активных систем – 2009". ИПУ РАН, 17 -19 ноября 2009. Т. 2. С. 165 -168. 27. Агасандян Г. А. Рандомизация портфеля опционов при использовании континуального критерия Va. R на дискретном рынке. М. : ВЦ РАН, 2010. 42 с. 28. Агасандян Г. А. О корректности семейств функций рисковых предпочтений инвестора для континуального критерия Va. R. М. : ВЦ РАН, 2010. 32 с.

CC-Va. R: Литература 28. Агасандян Г. А. О свойствах семейств функций рисковых предпочтений инвестора для CC-Va. R. / Труды 6 -й Московской международной конференции по Исследованию Операций (ORM 2010). Москва, 19 -22 октября 2010. МАКС Пресс. С. 441442. 29. Агасандян Г. А. Об эффективности рандомизации весов оптимального по континуальному критерию Va. R портфеля. / Материалы Четвертой международной конференции "Управление развитием крупномасштабных систем" (MLSD'2010). ИПУ РАН, 4 -6 октября 2010. С. 189 -191. 30. Агасандян Г. А. О параметризации функций рисковых предпочтений инвестора для CC-Va. R. / Материалы Четвертой международной конференции "Управление развитием крупномасштабных систем" (MLSD'2010). ИПУ РАН, 4 -6 октября 2010. С. 189 -191. 31. Агасандян Г. А. Многомерные финансовые рынки и CC-Va. R. / Труды ИПУ РАН, Специальный выпуск "Управление большими системами – сборник "Сетевые модели в управлении". М. : ИПУ РАН, 2010. Т. 39(1). С. 154 -165. ? ?

CC-Va. R: Литература 36. Агасандян Г. А. Применение CC-Va. R к некоторым классам вероятностных распределений для базовых активов. М. : ВЦ РАН, 2011. 44 с. 37. Агасандян Г. А. О выборе опционного базиса при использовании CC-Va. R на финансовых рынках. М. : ВЦ РАН, 2011. 46 с. 38. Агасандян Г. А. Применение континуального критерия Va. R на финансовых рынках. М. : ВЦ РАН, 2011. 299 с. 39. Агасандян Г. А. Многомерные рынки, α-опционы и портфели двумерных опционов. М. : ВЦ РАН, 2012. 33 с. 40. Агасандян Г. А. Базисные баттерфляи на двумерных опционных рынках и построение оптимальных по CC-Va. R портфелей. М. : ВЦ РАН, 2012. 37 с. 41. Агасандян Г. А. Базисные баттерфляи на трехмерных опционных рынках и построение оптимальных по CC-Va. R портфелей. 2012. ? ? с. Пример построения базиса из полных и усеченных баттерфляев и оптимального портфеля на трехмерном опционном рынке. М. : ВЦ РАН,

Многомерный рынок опционов