7.Крыло_sdwig.ppt
- Количество слайдов: 45
 Конструкция крыла Расчет элементов крыла на сдвиг
Конструкция крыла Расчет элементов крыла на сдвиг
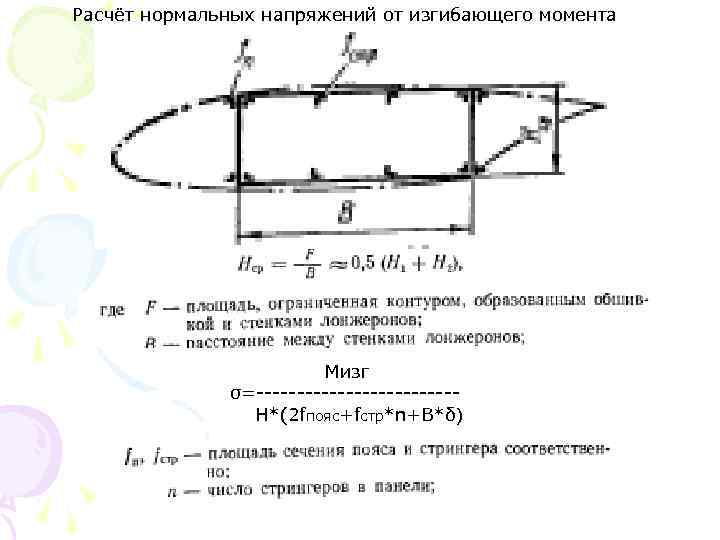 Расчёт нормальных напряжений от изгибающего момента Мизг σ=------------Н*(2 fпояс+fстр*n+B*δ)
Расчёт нормальных напряжений от изгибающего момента Мизг σ=------------Н*(2 fпояс+fстр*n+B*δ)
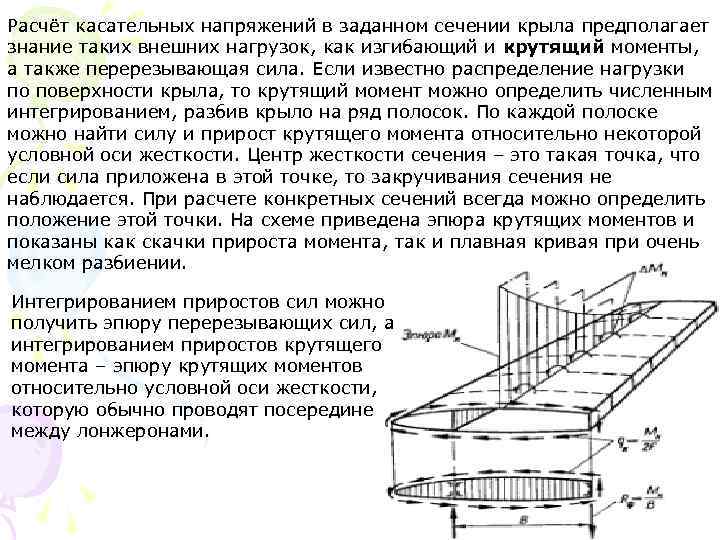 Расчёт касательных напряжений в заданном сечении крыла предполагает знание таких внешних нагрузок, как изгибающий и крутящий моменты, а также перерезывающая сила. Если известно распределение нагрузки по поверхности крыла, то крутящий момент можно определить численным интегрированием, разбив крыло на ряд полосок. По каждой полоске можно найти силу и прирост крутящего момента относительно некоторой условной оси жесткости. Центр жесткости сечения – это такая точка, что если сила приложена в этой точке, то закручивания сечения не наблюдается. При расчете конкретных сечений всегда можно определить положение этой точки. На схеме приведена эпюра крутящих моментов и показаны как скачки прироста момента, так и плавная кривая при очень мелком разбиении. Интегрированием приростов сил можно получить эпюру перерезывающих сил, а интегрированием приростов крутящего момента – эпюру крутящих моментов относительно условной оси жесткости, которую обычно проводят посередине между лонжеронами.
Расчёт касательных напряжений в заданном сечении крыла предполагает знание таких внешних нагрузок, как изгибающий и крутящий моменты, а также перерезывающая сила. Если известно распределение нагрузки по поверхности крыла, то крутящий момент можно определить численным интегрированием, разбив крыло на ряд полосок. По каждой полоске можно найти силу и прирост крутящего момента относительно некоторой условной оси жесткости. Центр жесткости сечения – это такая точка, что если сила приложена в этой точке, то закручивания сечения не наблюдается. При расчете конкретных сечений всегда можно определить положение этой точки. На схеме приведена эпюра крутящих моментов и показаны как скачки прироста момента, так и плавная кривая при очень мелком разбиении. Интегрированием приростов сил можно получить эпюру перерезывающих сил, а интегрированием приростов крутящего момента – эпюру крутящих моментов относительно условной оси жесткости, которую обычно проводят посередине между лонжеронами.
 В сечении крыла крутящий момент воспринимается замкнутым контуром, образованным обшивкой и лонжеронами крыла. Если носок крыла не имеет вырезов, то замкнутый контур образует обшивка носка и кессона крыла и задний лонжерон. Тогда касательные усилия в переднем лонжероне от кручения невелики. Касательный поток от кручения в замкнутом контуре можно определить по формуле Бредта: Где Мк – крутящий момент, а 2 F – так называемая Бредтовская площадь, т. е. удвоенная площадь замкнутого контура. Существенный вклад в потоки касательных усилий в стенках лонжеронов дают перерезывающие силы. Таким образом необходимо определить потоки от Q и Мкр. В некоторых зонах они складываются , а в других вычитаются. Касательные потоки от перерезывающей силы определяются по формуле Журавского; При этом статический момент определяется при условии, что в некоторой точке контур разомкнут. Обычно этот разрыв принимают на верхней панели посередине между лонжеронами Если в носке крыла имеются вырезы, например под предкрылок, то касательные потоки замыкаются на контуре между лонжеронами и тогда касательный поток от кручения в переднем лонжероне складывается с потоком от перерезывающей силы. Таким образом в полетных случаях нагружения поток в переднем лонжероне больше, чем в заднем. В посадочных и взлетных случаях, когда выпущен закрылок, крутящий момент на пикирование приводит к обратной картине и тогда максимальные касательные потоки возникают в заднем лонжероне. Крыло передает касательные потоки на бортовую нервюру, где они превращаются в вертикальную пару по переднему и заднему силовым шпангоутам фюзеляжа. Часть нагрузки переходит на обшивку фюзеляжа.
В сечении крыла крутящий момент воспринимается замкнутым контуром, образованным обшивкой и лонжеронами крыла. Если носок крыла не имеет вырезов, то замкнутый контур образует обшивка носка и кессона крыла и задний лонжерон. Тогда касательные усилия в переднем лонжероне от кручения невелики. Касательный поток от кручения в замкнутом контуре можно определить по формуле Бредта: Где Мк – крутящий момент, а 2 F – так называемая Бредтовская площадь, т. е. удвоенная площадь замкнутого контура. Существенный вклад в потоки касательных усилий в стенках лонжеронов дают перерезывающие силы. Таким образом необходимо определить потоки от Q и Мкр. В некоторых зонах они складываются , а в других вычитаются. Касательные потоки от перерезывающей силы определяются по формуле Журавского; При этом статический момент определяется при условии, что в некоторой точке контур разомкнут. Обычно этот разрыв принимают на верхней панели посередине между лонжеронами Если в носке крыла имеются вырезы, например под предкрылок, то касательные потоки замыкаются на контуре между лонжеронами и тогда касательный поток от кручения в переднем лонжероне складывается с потоком от перерезывающей силы. Таким образом в полетных случаях нагружения поток в переднем лонжероне больше, чем в заднем. В посадочных и взлетных случаях, когда выпущен закрылок, крутящий момент на пикирование приводит к обратной картине и тогда максимальные касательные потоки возникают в заднем лонжероне. Крыло передает касательные потоки на бортовую нервюру, где они превращаются в вертикальную пару по переднему и заднему силовым шпангоутам фюзеляжа. Часть нагрузки переходит на обшивку фюзеляжа.
 Основные допущения: При определении касательных напряжений Т исходят из общепринятых допущений теории тонкостенных стержней и оболочек: принимают, что напряжения Т по толщине обшивки не изменяются, а погонные касательные усилия(касательные потоки) q=T*δ в любой точке сечения направлены по касательной к средней линии сечения контура. Кроме того считают, что поперечные сечения крыла при кручении могут свободно депланировать, т. е. отдельные точки сечения могут выходить из плоскости сечения. Обычно расчет проводят не отделяя изгиб от кручения, т. е. смотрят одновременное действие перерезывающей силы и крутящего момента. При этом обязателен учет конусности крыла, который обычно позволяет существенно уменьшить срезающую силу Qу по сравнению с перерезывающей силой Q.
Основные допущения: При определении касательных напряжений Т исходят из общепринятых допущений теории тонкостенных стержней и оболочек: принимают, что напряжения Т по толщине обшивки не изменяются, а погонные касательные усилия(касательные потоки) q=T*δ в любой точке сечения направлены по касательной к средней линии сечения контура. Кроме того считают, что поперечные сечения крыла при кручении могут свободно депланировать, т. е. отдельные точки сечения могут выходить из плоскости сечения. Обычно расчет проводят не отделяя изгиб от кручения, т. е. смотрят одновременное действие перерезывающей силы и крутящего момента. При этом обязателен учет конусности крыла, который обычно позволяет существенно уменьшить срезающую силу Qу по сравнению с перерезывающей силой Q.
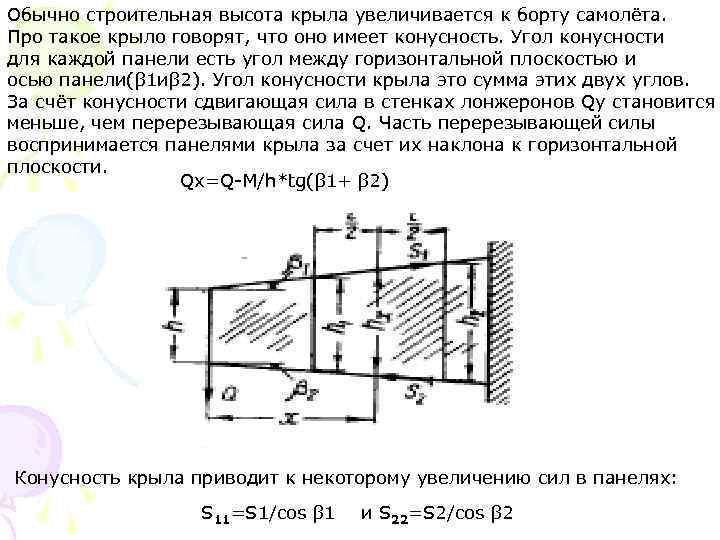 Обычно строительная высота крыла увеличивается к борту самолёта. Про такое крыло говорят, что оно имеет конусность. Угол конусности для каждой панели есть угол между горизонтальной плоскостью и осью панели(β 1 иβ 2). Угол конусности крыла это сумма этих двух углов. За счёт конусности сдвигающая сила в стенках лонжеронов Qу становится меньше, чем перерезывающая сила Q. Часть перерезывающей силы воспринимается панелями крыла за счет их наклона к горизонтальной плоскости. Qx=Q-M/h*tg(β 1+ β 2) Конусность крыла приводит к некоторому увеличению сил в панелях: S 11=S 1/cos β 1 и S 22=S 2/cos β 2
Обычно строительная высота крыла увеличивается к борту самолёта. Про такое крыло говорят, что оно имеет конусность. Угол конусности для каждой панели есть угол между горизонтальной плоскостью и осью панели(β 1 иβ 2). Угол конусности крыла это сумма этих двух углов. За счёт конусности сдвигающая сила в стенках лонжеронов Qу становится меньше, чем перерезывающая сила Q. Часть перерезывающей силы воспринимается панелями крыла за счет их наклона к горизонтальной плоскости. Qx=Q-M/h*tg(β 1+ β 2) Конусность крыла приводит к некоторому увеличению сил в панелях: S 11=S 1/cos β 1 и S 22=S 2/cos β 2
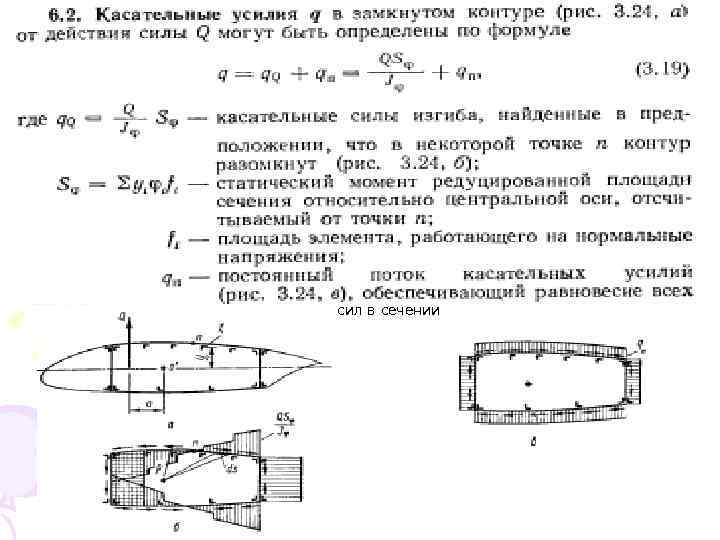 сил в сечении
сил в сечении
 Расчет рекомендуется делать в следующей последовательности: 1. Для каждого стрингера и пояса лонжерона в таблице задаются площадь поперечного сечения(с приведенной обшивкой), координаты хиу 2. Определяются суммарная площадь стрингеров и поясов лонжеронов с обшивкой, центр тяжести сечения и координаты х1 и у1 относительно новых центральных осей. 3. Вводится разрез в некоторой точке верхней панели. Начиная от точки разреза определяются статические моменты, а затем потоки касательных усилий от перерезывающей силы. Определяется момент MQот этих потоков относительно центра тяжести. Определяется поток от этого момента по формуле Бредта. Этот поток суммируется с потоками от Q.
Расчет рекомендуется делать в следующей последовательности: 1. Для каждого стрингера и пояса лонжерона в таблице задаются площадь поперечного сечения(с приведенной обшивкой), координаты хиу 2. Определяются суммарная площадь стрингеров и поясов лонжеронов с обшивкой, центр тяжести сечения и координаты х1 и у1 относительно новых центральных осей. 3. Вводится разрез в некоторой точке верхней панели. Начиная от точки разреза определяются статические моменты, а затем потоки касательных усилий от перерезывающей силы. Определяется момент MQот этих потоков относительно центра тяжести. Определяется поток от этого момента по формуле Бредта. Этот поток суммируется с потоками от Q.
 4. Определяется положение центра жеcткости. Для этого определяется момент от суммарных потоков и далее его нужно разделить на перерезывающую силу. Q. Получим расстояние от полюса до центра жесткости. 5. Определяется крутящий момент относительно центра жесткости Мож. Для этого нужно к крутящему моменту относительно условной оси жесткости Мк прибавить(отнять)произведение перерезывающей силы на расстояние между реальной и условной осями жесткости. 6. Определяется поток касательных усилий от крутящего момента Мож. Этот поток складывается с предыдущими потоками. Таким образом мы получаем касательные потоки в обшивке крыла и в стенках лонжеронов. 7. Разделив потоки на толщину стенки, определяем касательные напряжения в стенках лонжеронов и в обшивках крыла. 8. Определяются разрушающие касательные напряжения и запасы прочности по сдвигу. 9. Определяются нагрузки на элементы крепежа, соединяющие части конструкции, нагруженные сдвигом, и определяются запасы прочности по срезу крепежа и смятию пластин под крепежными элементами – болтами или заклепками.
4. Определяется положение центра жеcткости. Для этого определяется момент от суммарных потоков и далее его нужно разделить на перерезывающую силу. Q. Получим расстояние от полюса до центра жесткости. 5. Определяется крутящий момент относительно центра жесткости Мож. Для этого нужно к крутящему моменту относительно условной оси жесткости Мк прибавить(отнять)произведение перерезывающей силы на расстояние между реальной и условной осями жесткости. 6. Определяется поток касательных усилий от крутящего момента Мож. Этот поток складывается с предыдущими потоками. Таким образом мы получаем касательные потоки в обшивке крыла и в стенках лонжеронов. 7. Разделив потоки на толщину стенки, определяем касательные напряжения в стенках лонжеронов и в обшивках крыла. 8. Определяются разрушающие касательные напряжения и запасы прочности по сдвигу. 9. Определяются нагрузки на элементы крепежа, соединяющие части конструкции, нагруженные сдвигом, и определяются запасы прочности по срезу крепежа и смятию пластин под крепежными элементами – болтами или заклепками.








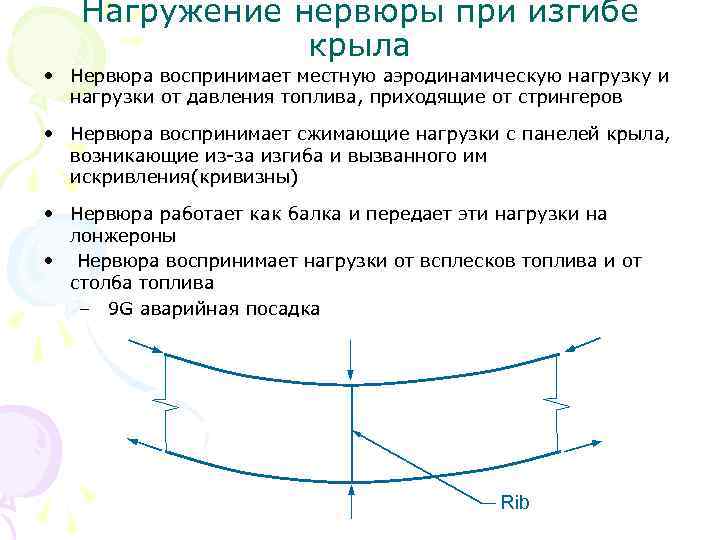 Нагружение нервюры при изгибе крыла • Нервюра воспринимает местную аэродинамическую нагрузку и нагрузки от давления топлива, приходящие от стрингеров • Нервюра воспринимает сжимающие нагрузки с панелей крыла, возникающие из-за изгиба и вызванного им искривления(кривизны) • Нервюра работает как балка и передает эти нагрузки на лонжероны • Нервюра воспринимает нагрузки от всплесков топлива и от столба топлива – 9 G аварийная посадка Rib
Нагружение нервюры при изгибе крыла • Нервюра воспринимает местную аэродинамическую нагрузку и нагрузки от давления топлива, приходящие от стрингеров • Нервюра воспринимает сжимающие нагрузки с панелей крыла, возникающие из-за изгиба и вызванного им искривления(кривизны) • Нервюра работает как балка и передает эти нагрузки на лонжероны • Нервюра воспринимает нагрузки от всплесков топлива и от столба топлива – 9 G аварийная посадка Rib





 σкр=k*E/(b/δ)2 τкр=k*E/(b/δ)2 σ/σкр+(τ/τкр)2=1 2. 2 2. 3
σкр=k*E/(b/δ)2 τкр=k*E/(b/δ)2 σ/σкр+(τ/τкр)2=1 2. 2 2. 3


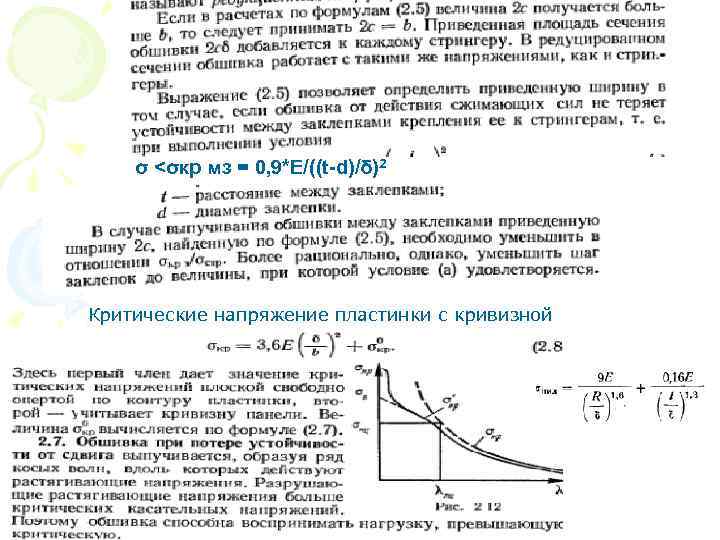 σ <σкр мз = 0, 9*Е/((t-d)/δ)2 Критические напряжение пластинки с кривизной
σ <σкр мз = 0, 9*Е/((t-d)/δ)2 Критические напряжение пластинки с кривизной
 Skin/Stringer Panel Compression Failure
Skin/Stringer Panel Compression Failure
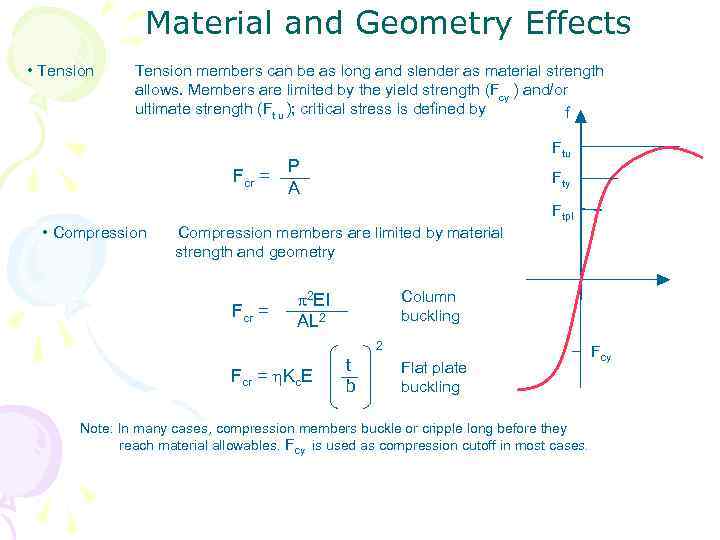 Material and Geometry Effects • Tension members can be as long and slender as material strength allows. Members are limited by the yield strength (Fcy ) and/or ultimate strength (Ft u ); critical stress is defined by f ty Fcr = Ftu P A Fty Ftpl • Compression members are limited by material strength and geometry Fcr = 2 EI AL 2 Column buckling 2 Fcr = Kc. E t b Flat plate buckling Note: In many cases, compression members buckle or cripple long before they reach material allowables. Fccy is used as compression cutoff in most cases. y Fcy
Material and Geometry Effects • Tension members can be as long and slender as material strength allows. Members are limited by the yield strength (Fcy ) and/or ultimate strength (Ft u ); critical stress is defined by f ty Fcr = Ftu P A Fty Ftpl • Compression members are limited by material strength and geometry Fcr = 2 EI AL 2 Column buckling 2 Fcr = Kc. E t b Flat plate buckling Note: In many cases, compression members buckle or cripple long before they reach material allowables. Fccy is used as compression cutoff in most cases. y Fcy
 Note: See also Gere & Timoshenko, Mechanics of Materials, PWS, 1984, Chapter 9
Note: See also Gere & Timoshenko, Mechanics of Materials, PWS, 1984, Chapter 9
 Геометрические характеристики Radius of gyration(радиус инерции) End fixity coefficient(коэф защемления) c Effective length Slenderness ratio(удлинение) Note: The moment of inertia, I, is the minimum moment of inertia. Always use Imin and min.
Геометрические характеристики Radius of gyration(радиус инерции) End fixity coefficient(коэф защемления) c Effective length Slenderness ratio(удлинение) Note: The moment of inertia, I, is the minimum moment of inertia. Always use Imin and min.
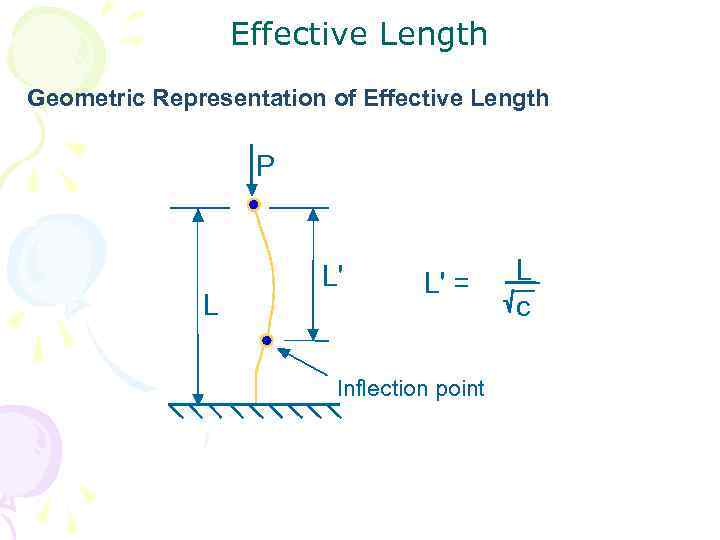 Effective Length Geometric Representation of Effective Length P L L' L' = Inflection point L c
Effective Length Geometric Representation of Effective Length P L L' L' = Inflection point L c
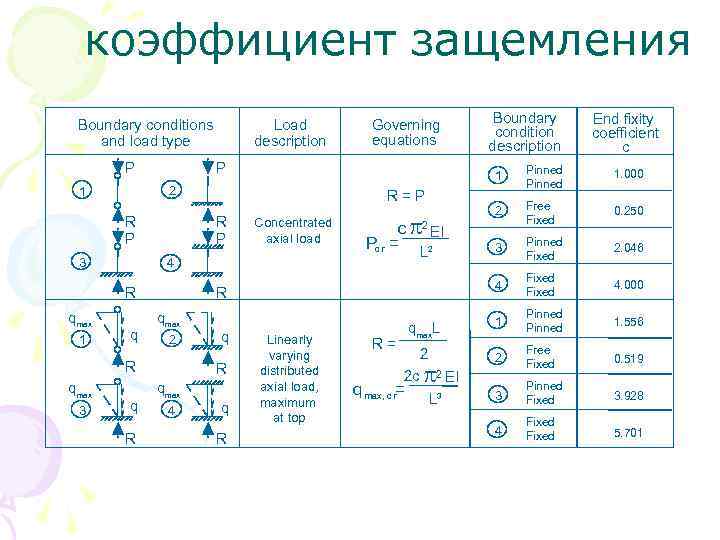 коэффициент защемления Boundary conditions and load type P R P 3 q R q max 3 q R Pinned 1. 000 2 Free Fixed 0. 250 3 Pinned Fixed 2. 046 Fixed 4. 000 q max. L 1 Pinned 1. 556 2 2 Free Fixed 0. 519 3 Pinned Fixed 3. 928 4 Fixed 5. 701 c 2 EI Pc r = L 2 R 2 q R q max 4 q R End fixity coefficient c 4 Concentrated axial load 4 q max Boundary condition description 1 R=P R 1 Governing equations P 2 1 q max Load description Linearly varying distributed axial load, maximum at top R= 2 c q max, c r= 2 EI L 3
коэффициент защемления Boundary conditions and load type P R P 3 q R q max 3 q R Pinned 1. 000 2 Free Fixed 0. 250 3 Pinned Fixed 2. 046 Fixed 4. 000 q max. L 1 Pinned 1. 556 2 2 Free Fixed 0. 519 3 Pinned Fixed 3. 928 4 Fixed 5. 701 c 2 EI Pc r = L 2 R 2 q R q max 4 q R End fixity coefficient c 4 Concentrated axial load 4 q max Boundary condition description 1 R=P R 1 Governing equations P 2 1 q max Load description Linearly varying distributed axial load, maximum at top R= 2 c q max, c r= 2 EI L 3

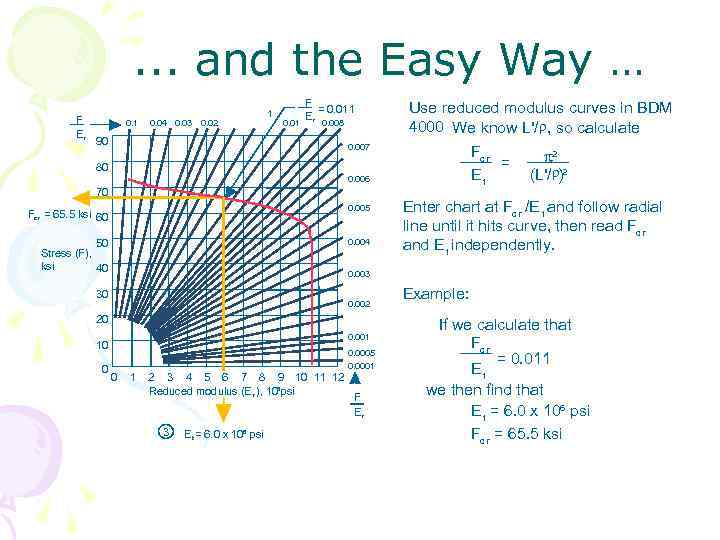 . . . and the Easy Way … F Er 0. 1 0. 04 0. 03 0. 02 1 0. 01 F = 0. 011 Er 0. 008 90 Use reduced modulus curves in BDM 4000 We know L'/ , so calculate 0. 007 Fc r = Et 80 0. 006 70 0. 005 Fc r = 65. 5 ksi 60 0. 004 50 Stress (F), ksi 40 (L'/ )2 Enter chart at Fc r /E t and follow radial line until it hits curve, then read Fc r and E t independently. 0. 003 30 0. 002 20 0. 001 10 0 2 0. 0005 0. 0001 0 1 2 3 4 5 6 7 8 9 10 11 12 Reduced modulus (E r ), 106 psi 3 E t = 6. 0 x 106 psi F Er Example: If we calculate that Fc r = 0. 011 Et we then find that E t = 6. 0 x 106 psi Fc r = 65. 5 ksi
. . . and the Easy Way … F Er 0. 1 0. 04 0. 03 0. 02 1 0. 01 F = 0. 011 Er 0. 008 90 Use reduced modulus curves in BDM 4000 We know L'/ , so calculate 0. 007 Fc r = Et 80 0. 006 70 0. 005 Fc r = 65. 5 ksi 60 0. 004 50 Stress (F), ksi 40 (L'/ )2 Enter chart at Fc r /E t and follow radial line until it hits curve, then read Fc r and E t independently. 0. 003 30 0. 002 20 0. 001 10 0 2 0. 0005 0. 0001 0 1 2 3 4 5 6 7 8 9 10 11 12 Reduced modulus (E r ), 106 psi 3 E t = 6. 0 x 106 psi F Er Example: If we calculate that Fc r = 0. 011 Et we then find that E t = 6. 0 x 106 psi Fc r = 65. 5 ksi

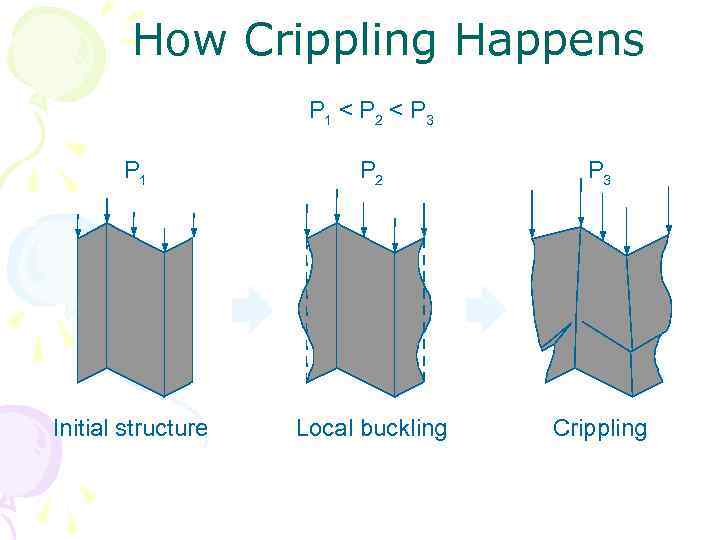 How Crippling Happens P 1 < P 2 < P 3 P 1 P 2 P 3 Initial structure Local buckling Crippling
How Crippling Happens P 1 < P 2 < P 3 P 1 P 2 P 3 Initial structure Local buckling Crippling
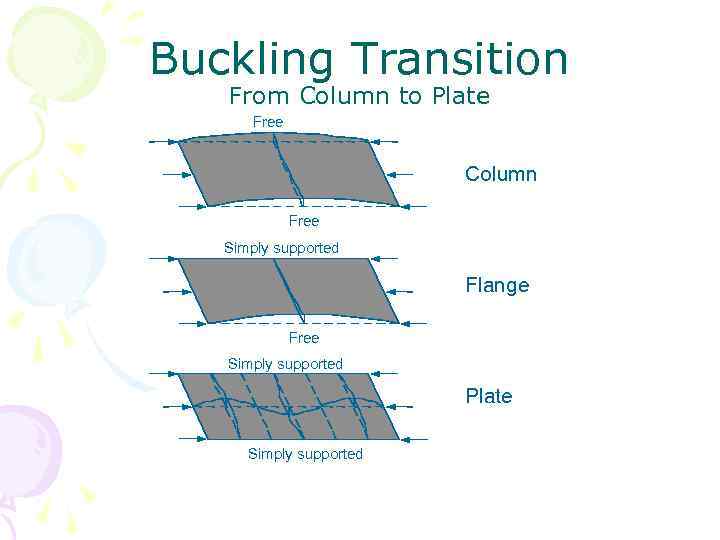 Buckling Transition From Column to Plate Free Column Free Simply supported Flange Free Simply supported Plate Simply supported
Buckling Transition From Column to Plate Free Column Free Simply supported Flange Free Simply supported Plate Simply supported
 Flat Plate Buckling Axial Compression
Flat Plate Buckling Axial Compression
 Flat Plate Buckling Shear
Flat Plate Buckling Shear
 Buckling Constant • Governing equation: • Current curves in BDM 6520 cover in-plane axial, shear, and moment loading cases for the following plate geometries: - Rectangle - Triangle - Trapezoid - Parallelogram - Square plate with centrally located circular cutouts • Soon-to-be-released plate buckling geometries • Rectangular plates with centrally located circular cutouts • Square plates with non-centrally located circular cutouts Note: Current curves do not cover all loading cases for every shape; finite element analysis or testing is required for situations.
Buckling Constant • Governing equation: • Current curves in BDM 6520 cover in-plane axial, shear, and moment loading cases for the following plate geometries: - Rectangle - Triangle - Trapezoid - Parallelogram - Square plate with centrally located circular cutouts • Soon-to-be-released plate buckling geometries • Rectangular plates with centrally located circular cutouts • Square plates with non-centrally located circular cutouts Note: Current curves do not cover all loading cases for every shape; finite element analysis or testing is required for situations.
 Floorbeam Buckling
Floorbeam Buckling





