Конспект лекций по ТОЭ Подготовлен Степановым К С

Конспект лекций по ТОЭ Подготовлен: Степановым К. С. , Беловой Л. В. , Кафедра теоретической и общей электротехники. Лекция 6 b Степанов Константин Сергеевич

Переходные процессы в цепях с резистором, индуктивностью и ёмкостью часть1 Степанов Константин Сергеевич

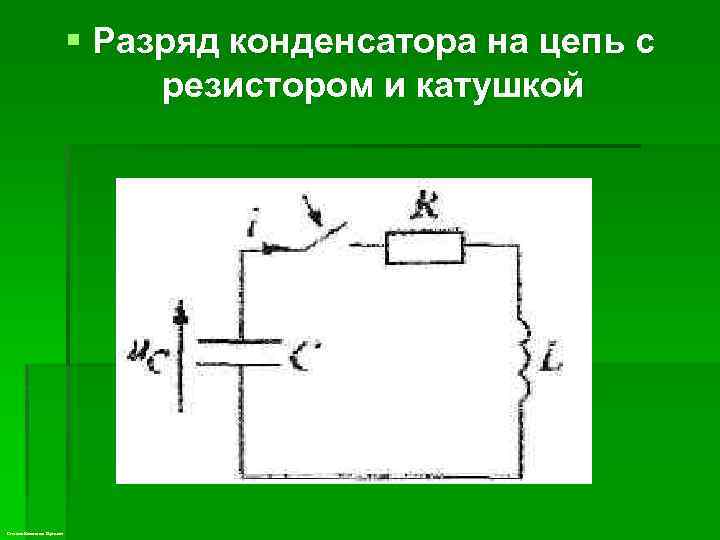§ Разряд конденсатора на цепь с резистором и катушкой Степанов Константин Сергеевич

§ Пусть в цепи, изображенной выше, конденсатор был заряжен до напряжения uc(0 -) = Uo. Исследуем процессы в контуре, образованном резистором, конденсатором и катушкой после замыкания ключа в момент t = 0. Так как источники в цепи отсутствуют, то установившиеся составляющие равны нулю. Решение будет состоять из одной свободной составляющей. Степанов Константин Сергеевич

Составление характеристического уравнения. § По второму закону Кирхгофа t ≥ 0 имеем: § Учитывая, что , получаем дифференциальное уравнение второго порядка для свободной составляющей напряжения. Степанов Константин Сергеевич

Характеристическое уравнение при этом имеет вид: Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения Степанов Константин Сергеевич

§ В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений. Степанов Константин Сергеевич

Апериодический разряд конденсатора на катушку и резистор § Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию или , то корни характеристического уравнения контура вещественные, различные, т. е. p 1 ≠ p 2, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением Степанов Константин Сергеевич

§ где A 1 и А 2 - постоянные интегрирования, определяемые из начальных, условий. Свободный ток равен Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Степанов Константин Сергеевич

Поэтому их переходные значения равны свободным составляющим: Определим из начальных условий постоянные интегрирования A 1 и А 2. При t = 0, uc(0) = U 0 и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем: U 0 = A 1 + А 2; 0 = A 1 p 1 + А 2 р 2 Степанов Константин Сергеевич

Отсюда A 1 = U 0 p 2 / (p 2 – p 1); А 2 = -U 0 p 1 / (р2 – p 1) С учетом начальных условий запишем Произведение корней по теореме Виета: p 1 р2 = 1 / (LC), следовательно, ток Степанов Константин Сергеевич

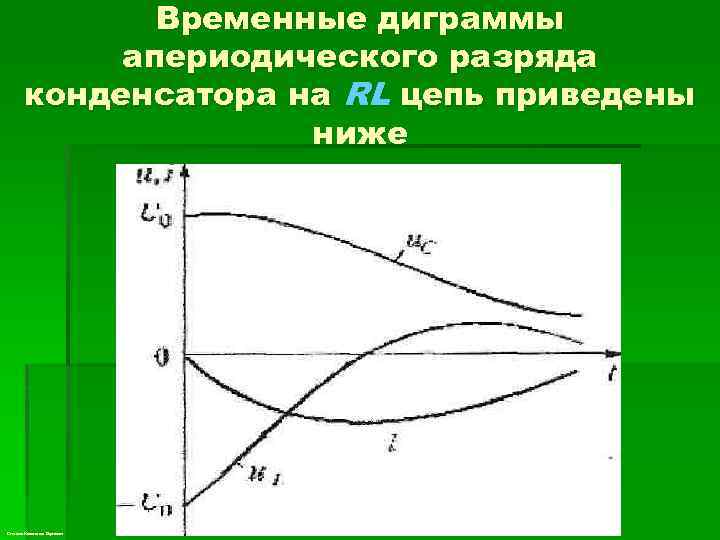Временные диграммы апериодического разряда конденсатора на RL цепь приведены ниже Степанов Константин Сергеевич

§ Графики зависимости тока и напряжения от времени, показанные выше позволяют говорить об апериодическом разряде конденсатора. Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т. е. функция uc(t) - убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Степанов Константин Сергеевич

Выводы: 1. Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения. 2. При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение. 3. Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля. Степанов Константин Сергеевич

§ Предельный апериодический разряд конденсатора на катушку и резистор При соотношении параметров контура из конденсатора, катушки и резистора § где: Rкр - критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные: Степанов Константин Сергеевич

Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходное напряжение и переходный ток в этом случае имеют вид: Степанов Константин Сергеевич

При начальных условиях uc(0) = U 0; i(0) = 0 находим: . A 1 – U 0; А 2 = -р. U 0. С учетом найденных постоянных интегрирования получаем решения: Зависимости i, uc, u. L такие же, как для апериодического разряда. Степанов Константин Сергеевич

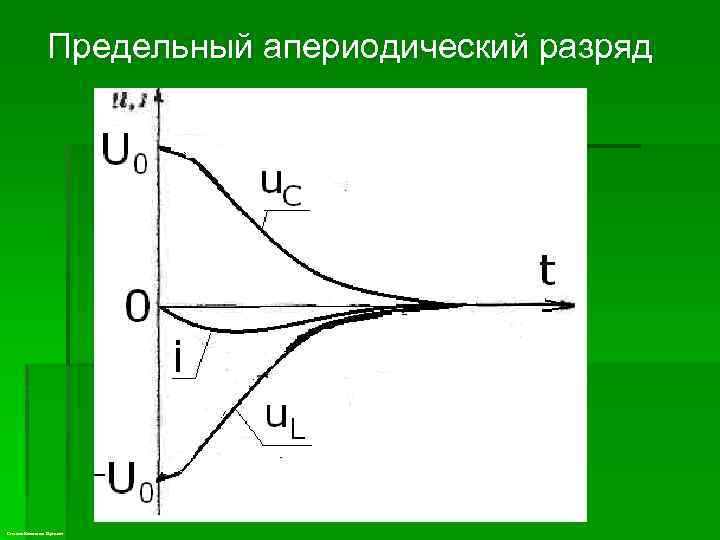Предельный апериодический разряд Степанов Константин Сергеевич

Периодический разряд конденсатора на цепь с резистором и катушкой § При соотношении параметров контура из конденсатора, катушки и резистора , где Rкр - критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные Степанов Константин Сергеевич

Благодарю за внимание Степанов Константин Сергеевич