Консервативные системы Примеры задач Теорема Лагранжа Консервативная

Консервативные системы. Примеры задач

Теорема Лагранжа Консервативная система при заданных перемещениях находится в состоянии равновесия (устойчивом или неустойчивом), если ее полная потенциальная энергия принимает экстремальное значение l Чтобы в заданном положении система сохраняла равновесие достаточно, чтобы вариация полной потенциальной энергии системы была равна нулю: l

Теорема Лагранжа l Записывая полную системы, получим: потенциальную энергию

Теорема Лагранжа l Поскольку вариации перемещений, вообще говоря, произвольны, а внешние силы потенциальны (следовательно потенциальны и обобщенные внешние силы), то Это еще одна формулировка теоремы Лагранжа

Теорема Лагранжа l Выразим потенциальную энергию деформаций в общем виде: l Тогда по теореме Лагранжа получим: внутренних

Метод перемещений l В методе перемещений в качестве независимых переменных выступают перемещения узлов физической модели конструкции. l Стержневая модель представляется совокупностью призматических стержней, соединенных между собой в узлах. l В зависимости от напряженного состояния стержней узлы могут представлять собой шарниры для ферменных конструкций или жесткие диски (жесткие тела в пространственном случае) для рамных и смешанных конструкций. l Каждый узел имеет столько перемещений (степеней свободы) сколько необходимо для однозначного определения его положения в пространстве. l Для шарнирного узла на плоскости – 2 степени свободы; в пространстве – 3. l Для жесткого диска на плоскости – 3 степени свободы (2 -е линейных, 1 -а угловая). Для жесткого тела в пространстве – 6 степеней свободы (3 -и линейных, 3 угловых).

Метод перемещений l Совокупность всех перемещений (степеней свободы) узлов модели представляет собой систему обобщенных координат, которая может быть представлена вектором {q} l К узлам модели, вдоль направлений обобщенных координат qi могут быть приложены обобщенные силы Qi (сила прикладывается по соответствующему направлению или степени свободы). Совокупность обобщенных сил составляет вектор {Q}. l Связь между {Q} и {q} может быть установлена по теореме Лагранжа: l Вектор {q} может представлять собой все абсолютные перемещения модели, включая перемещения как жесткого целого. При этом матрица жесткости [L] является полной матрицей жесткости и , кроме того, особенной (ее определитель равен нулю). В этом случае вектор обобщенных сил {Q} включает в себя и реакции внешних связей.

Метод перемещений l Представление стержневой модели совокупностью призматических стержней, соединенных в узлах, положение которых однозначно определяется заданным числом обобщенных координат позволяет автоматизировать процесс формирования матрицы жесткости [L] физической модели конструкции. l Потенциальная энергия деформации системы может быть представлена в виде: l где сжатии - потенциальная энергия деформации при растяжении- l - потенциальная энергия деформации при изгибе l - потенциальная энергия деформации при сдвиге l - потенциальная энергия деформации при кручении

Метод перемещений. МЖ стержня l Рассмотрим отдельно взятый призматический стержень в его собственной (локальной) системе координат y w 3 , R 3 l l Между этими силами существуют зависимости, вытекающие из уравнений равновесия стержня: w 6 , R 6 w 4 , R 4 w 1 , R 1 w 2 , R 2 Силы Ri представляют собой реакции со стороны соседних стержней и, кроме этого, учитывают внешние обобщенные силы, приложенные в узлах стержня. w 5 , R 5 x

Метод перемещений. МЖ стержня y l w 6 , R 6 w 3 , R 3 w 4 , R 4 w 1 , R 1 x Эпюры сил и моментов в стержне l Силы Ri представляют собой реакции со стороны соседних стержней и, кроме этого, учитывают внешние обобщенные силы, приложенные в узлах стержня. l Между этими силами существуют зависимости, вытекающие из уравнений равновесия стержня: w 5 , R 5 w 2 , R 2 N x -R 1 Qy Mz R 3 R 2 x R 6 x

Метод перемещений. МЖ стержня y l w 6 , R 6 w 3 , R 3 w 4 , R 4 w 1 , R 1 w 5 , R 5 w 2 , R 2 N x -R 1 Qy Mz R 3 R 2 x R 6 x x Подставляя в выражение для потенциальной энергии деформации получим:

Метод перемещений. МЖ стержня y w 3 , R 3 l w 6 , R 6 w 4 , R 4 w 1 , R 1 w 2 , R 2 l Тогда в матричной форме x w 5 , R 5 Перемещения левого узла, относительно правого могут быть получены по теореме Кастилиано:

Метод перемещений. МЖ стержня y w 3 , R 3 l w 6 , R 6 w 4 , R 4 w 1 , R 1 w 2 , R 2 w 5 , R 5 x Преобразуя, получим:

Метод перемещений. МЖ стержня y w 3 , R 3 l w 6 , R 6 w 4 , R 4 w 1 , R 1 w 2 , R 2 w 5 , R 5 Учитывая, что работа сил на соответствующих перемещениях равна l Получим: x

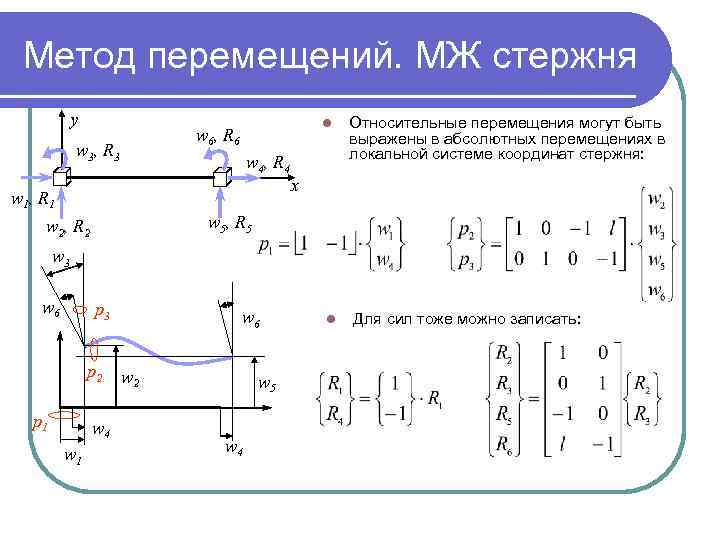Метод перемещений. МЖ стержня y l w 6 , R 6 w 3 , R 3 w 4 , R 4 w 1 , R 1 Относительные перемещения могут быть выражены в абсолютных перемещениях в локальной системе координат стержня: x w 5 , R 5 w 2 , R 2 w 3 w 6 p 3 p 2 p 1 w 4 w 1 w 6 w 2 w 5 w 4 l Для сил тоже можно записать:

Метод перемещений. МЖ стержня y l w 6 , R 6 w 3 , R 3 w 4 , R 4 w 1 , R 1 w 5 , R 5 w 2 , R 2 w 3 w 6 p 3 p 2 p 1 w 4 w 1 w 6 w 2 w 5 w 4 x Подставляя полученные выражения в потенциальную энергию деформации получим:

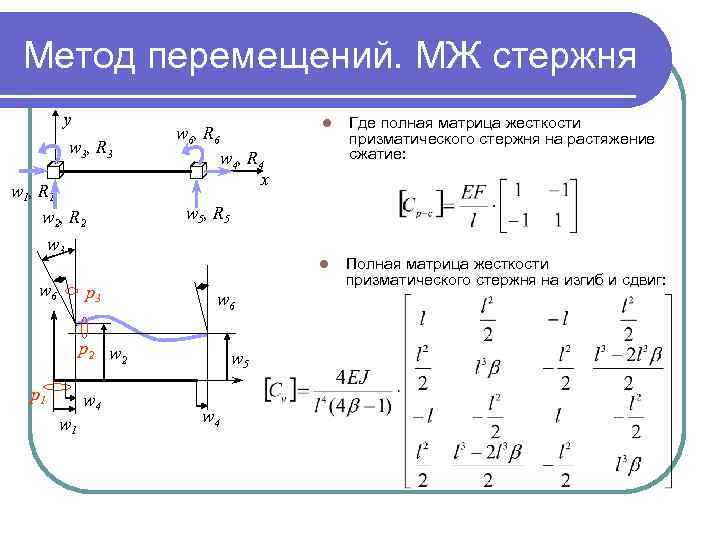Метод перемещений. МЖ стержня y w 1 , R 1 w 2 , R 2 Где полная матрица жесткости призматического стержня на растяжение сжатие: l w 3 , R 3 l w 6 , R 6 Полная матрица жесткости призматического стержня на изгиб и сдвиг: w 4 , R 4 x w 5 , R 5 w 3 w 6 p 2 w 2 p 1 w 4 w 1 w 5 w 4

Метод перемещений. МЖ стержня y w 3 , R 3 w 1 , R 1 w 2 , R 2 l w 6 , R 6 w 4 , R 4 x w 5 , R 5 w 3 w 6 p 2 w 2 p 1 w 4 w 1 w 5 w 4 Или, учитывая, что

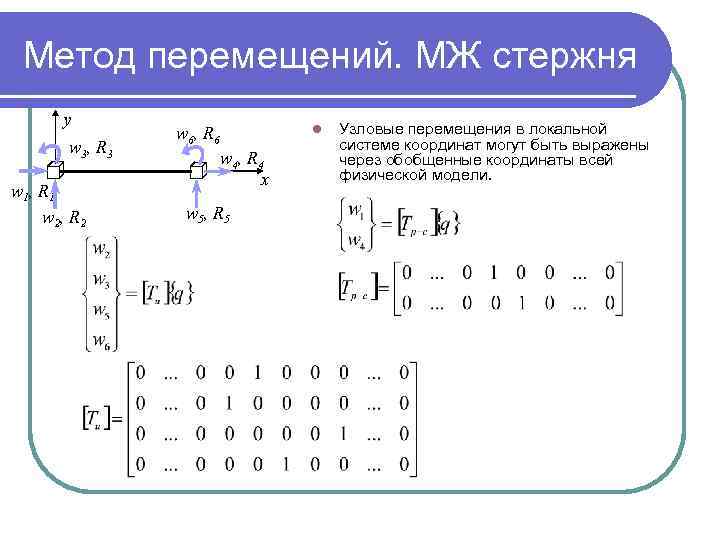Метод перемещений. МЖ стержня y w 3 , R 3 w 1 , R 1 w 2 , R 2 l w 6 , R 6 w 4 , R 4 x w 5 , R 5 Узловые перемещения в локальной системе координат могут быть выражены через обобщенные координаты всей физической модели.

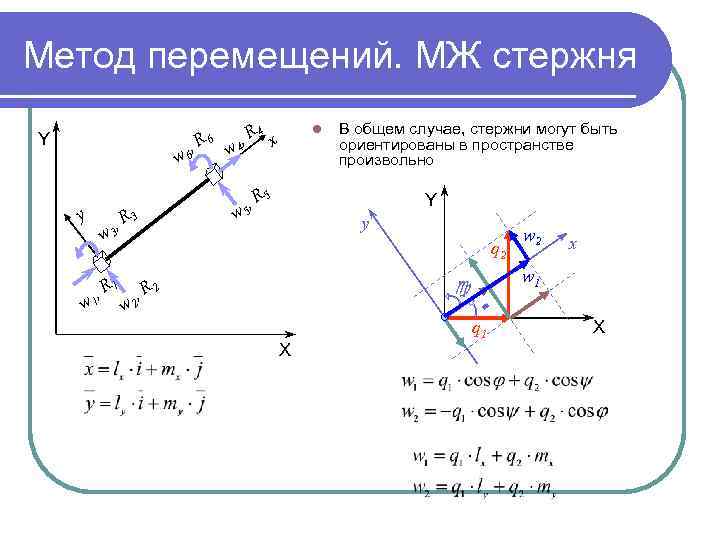Метод перемещений. МЖ стержня Y , R 6 w 6 y w , R 3 3 l , R 4 x w 4 w , R 5 5 В общем случае, стержни могут быть ориентированы в пространстве произвольно Y y q 2 c , R 1 2, R 2 w 1 w Х w 2 x w 1 w q 1 Х

Метод перемещений. МЖ стержня R 4 , R 6 w 4, x w 6 Y y , w 3 R 3 w , R 5 5 , R 1 , R 2 w 1 w 2 Х l В таком случае матрица преобразования координат (перемещений) будет следующей:

Метод перемещений. Последовательность вычислений ü Формирование матрицы жесткости системы (модели) ü Цикл по стержням: Ø Ø Вычисление направляющих косинусов осей докальной системы координат стержня Ø Вычисление матриц [Cр-с], [Cи], [Тр-с], [Ти] Ø ü Вычисление длины стержня по заданным декартовым координатам улов Конец цикла по стержням Вычисление вектора перемещений (в глобальной системе координат) по заданному вектору сил:

Метод перемещений. Последовательность вычислений Вычисление усилий и моментов в стержнях ü ü Цикл по стержням: Ø Конец цикла по стержням

Решение задачи C l 4 1. Обозначаем области вне конструкции. Обход по часовой стрелке 2. Обозначаем области внутри конструкции. Обход может быть любой 3 7 1 F l Построим диаграмму Кремоны P l 3 6 5 B 1 D 2 E 3. Строим диаграмму Кремоны A 5 4 2 d c f b a e

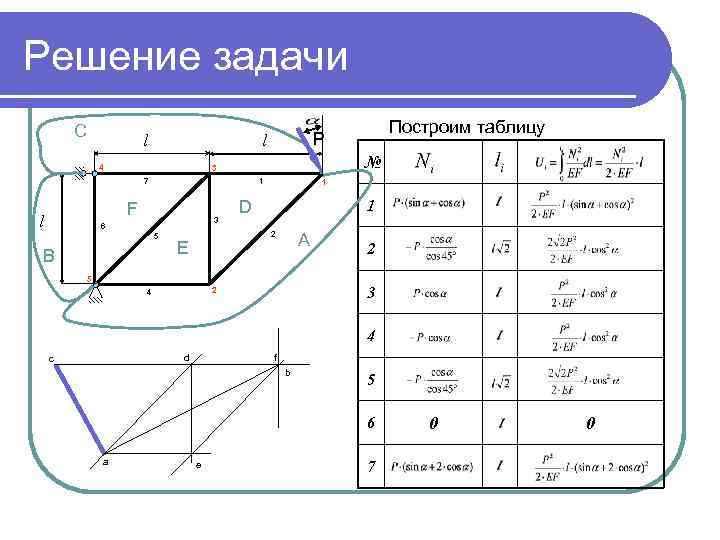Решение задачи C l 4 № 3 7 1 F l 3 6 5 B 1 1 D 2 E A 5 2 3 2 4 Построим таблицу P l 4 d c f b 5 6 a e 7 0 0

Решение задачи C l 4 3 7 1 F l P l 3 6 5 B 5 4 1 qy D 2 E 2 Запишем внутреннюю энергию деформации qx A

Решение задачи C l 4 1 F 3 6 5 B 1 G A 5 P 2 2 3 2 4 № 1 D 2 E Построим таблицу P 1 3 7 l P l 4 d c f b 5 6 g a e 7 0 0

Решение задачи C l 4 G 3 7 1 F l P 1 l 3 6 5 B D 2 E 5 4 1 2 A P 2 Запишем внутреннюю энергию деформации q 2 q 1

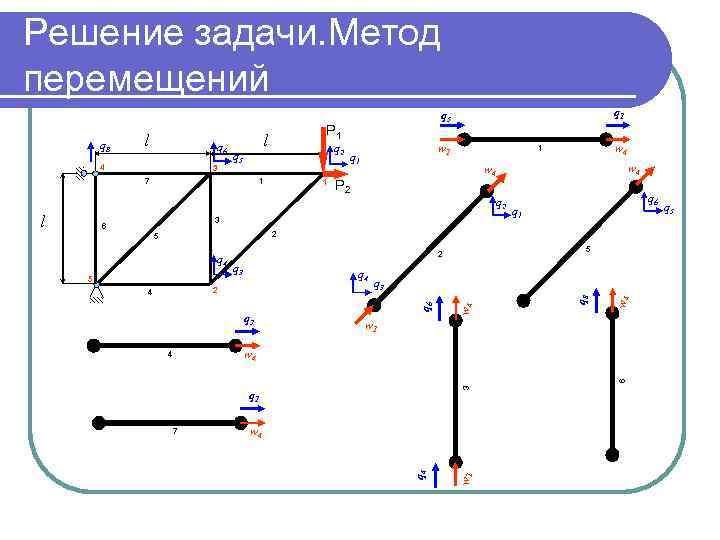Решение задачи. Метод перемещений q 6 4 3 P 1 l q 5 7 q 2 1 1 w 1 q 1 w 4 P 2 q 2 3 6 q 1 2 q 3 q 4 2 4 q 3 w 4 5 5 2 q 6 q 4 w 4 5 w 1 w 4 3 6 4 q 1 w 4 w 1 7 q 4 l w 4 1 q 8 l q 1 q 5

Решение задачи. Метод перемещений q 1 q 5 w 1 w 4 q 2 2 q 4 q 3 w 1 q 1

w 4 w 1 q 4 3 q 6 Решение задачи. Метод перемещений q 3 4 w 4

Решение задачи. Метод перемещений w 4 q 6 q 5 w 4 6 q 8 5 q 1 7 w 4

Решение задачи. Метод перемещений Запишем внутреннюю энергию деформации

Решение задачи. Метод перемещений Запишем внутреннюю энергию деформации

Решение задачи. Метод перемещений l Записывая полную системы, получим: потенциальную энергию

Решение задачи. Метод перемещений

Решение задачи. Метод перемещений Окончательно получим:

Решение задачи. Метод перемещений Матрица жесткости призматического стержня на изгиб