Конические проекции Актуальность исследования определяется тем что

Конические проекции

Актуальность исследования определяется тем, что при создании любых карт важное значение имеет вопрос о выборе картографических проекций, обеспечивающих оптимальное решение по этим картам различных задач.

Земную поверхность нельзя развернуть на плоскости, поэтому то или иное изображение земной поверхности или некоторой части ее на плоскости будет иметь искажения и длин, и углов, и площадей. Наиболее подобное изображение земной поверхности дает глобус.

Глобус является прекрасным учебным пособием, но не может служить для детального изучения отдельных стран и решения на нем инженерных и научных задач. Подробное изображение отдельных территорий, областей и государств можно дать только на карте, на которую географические элементы переносятся с земного эллипсоида искусственными приемами. «Изучение различных способов изображения земной поверхности на плоскости и составляет предмет математической картографии. А само изображение земной поверхности на плоскости мы будем называть картографической проекцией или просто картой» .

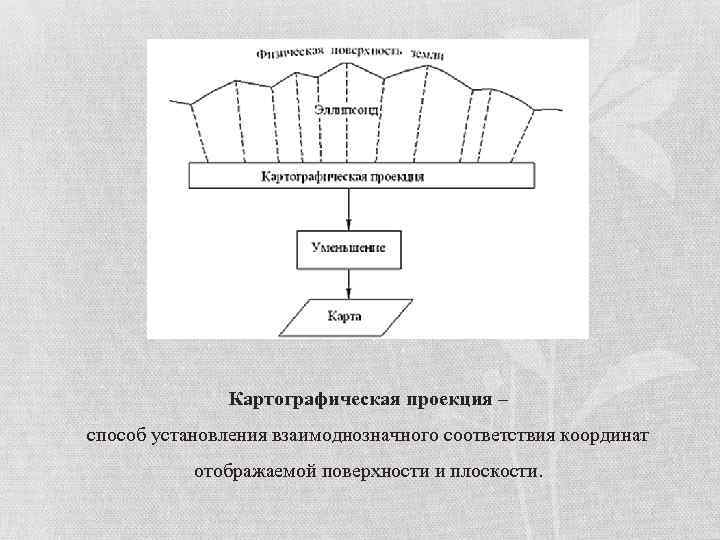Картографическая проекция – способ установления взаимоднозначного соответствия координат отображаемой поверхности и плоскости.

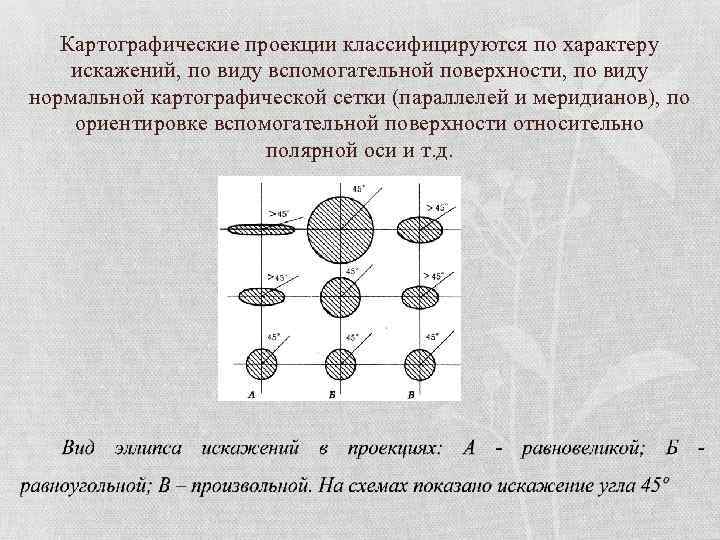Картографические проекции классифицируются по характеру искажений, по виду вспомогательной поверхности, по виду нормальной картографической сетки (параллелей и меридианов), по ориентировке вспомогательной поверхности относительно полярной оси и т. д.

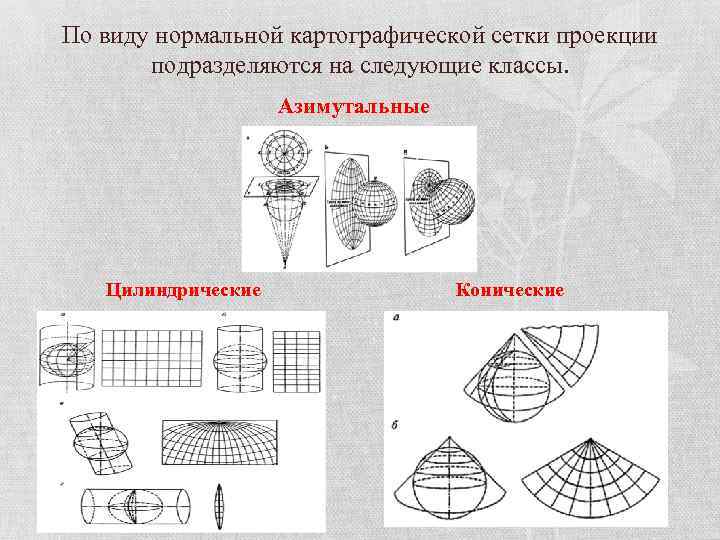По виду нормальной картографической сетки проекции подразделяются на следующие классы. Азимутальные Цилиндрические Конические

Конические проекции Сущность построения нормальных конических проекций заключается в том, что на боковую поверхность конуса проектируются параллели и меридианы с поверхности глобуса. При этом ось конуса совпадает с осью глобуса, а конус касается по одной (или двум, если он секущий) параллели, которая так и называется – параллель касания, она же линия нулевых искажений.

Равнопромежуточная коническая проекция Как предполагает само название, все параллели находятся на равном расстоянии друг от друга, пересекая меридианы через одинаковые интервалы. Таким образом, основное условие равнопромежуточных проекций выражается так: а=1 или b= 1; р = а или р = b.

Равноугольная коническая проекция Ламберта Данная проекция является равноугольной (конформной), следовательно в ней сохраняется подобие малых форм и направление как на мелко-, так и на крупномасштабных картах. Площади имеют минимальные искажения около стандартных параллелей. Масштаб площадей уменьшается в промежутке между стандартными параллелями и увеличивается за их пределами.

Равновеликая коническая проекция Альберса Обычно используется для небольших регионов или стран, вытянутых в направлении с востока на запад, а не для континентов. Сохраняет углы между меридианами и параллелями. Выполняется попытка уменьшить искажение формы и линейного масштаба, но эти характеристики не являются действительно точными. В этом примере показано, как эта проекция выглядит, если ее применить ко всей Земле.

Конические проекции чаще всего выбирали для создания карт бывшего СССР. Наименьшее количество искажений при конических проекциях приходилось на параллели 47° северной широты и 62° северной долготы. Это очень удобно, поскольку между указанными параллелями размещались основные хозяйственные зоны этого государства и здесь была сосредоточена максимальная нагрузка карт. Зато в конических проекциях сильно искажаются районы, лежащие в высоких широтах и акватории Северного Ледовитого океана.

Спасибо за внимание!