Лекция01_комп моделирование.ppt
- Количество слайдов: 66
 Компьютерное моделирование
Компьютерное моделирование
 Цель курса Показать возможность использования персонального компьютера как экспериментальной установки для проведения физических опытов; l познакомить с методами постановки компьютерного эксперимента в физике; l применить на практике численные методы решения физических задач. l
Цель курса Показать возможность использования персонального компьютера как экспериментальной установки для проведения физических опытов; l познакомить с методами постановки компьютерного эксперимента в физике; l применить на практике численные методы решения физических задач. l
 l Основные применения компьютеров в физических исследованиях – управление экспериментом (этих вопросов касаться не будем) и моделирование.
l Основные применения компьютеров в физических исследованиях – управление экспериментом (этих вопросов касаться не будем) и моделирование.
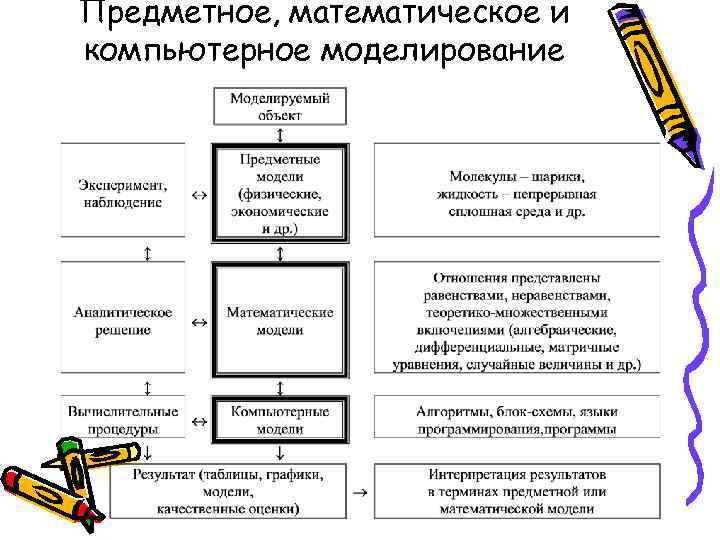 Предметное, математическое и компьютерное моделирование
Предметное, математическое и компьютерное моделирование
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Физический прибор Калибровка Измерение Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Физический прибор Калибровка Измерение Анализ данных
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Калибровка Измерение Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Калибровка Измерение Анализ данных
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Измерение Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Измерение Анализ данных
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Анализ данных
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Расчет Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Расчет Анализ данных
 Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Расчет Анализ данных
Аналогии между вычислительным и компьютерным экспериментами Лабораторный Вычислительный эксперимент Образец Модель Физический прибор Программа для компьютера Калибровка Тестирование программы Измерение Расчет Анализ данных
 • В дальнейшем нас будут интересовать этапы физического и математического моделирования (теория, вспоминаем, изучаем новое), • компьютерное моделирование – алгоритмы и программы (изучаем, знакомимся и сами пишем программы), • последний этап – интерпретация результатов на языке физической поставленной задачи.
• В дальнейшем нас будут интересовать этапы физического и математического моделирования (теория, вспоминаем, изучаем новое), • компьютерное моделирование – алгоритмы и программы (изучаем, знакомимся и сами пишем программы), • последний этап – интерпретация результатов на языке физической поставленной задачи.
 На примере моделирования падения тел в воздухе рассмотрим схему: • • • Физическая модель предполагает, например, что тело – материальная точка (форма не важна, понятно, что есть модели, где форма важна и даже очень!), сила сопротивления воздуха пропорциональна, например, квадрату скорости, коэффициент сопротивления должен быть известен, ускорение свободного падения не зависит от широты и равно g≈9. 8 m/c 2. Выполняются законы нерелятивистской механики. И т. п. Математическая модель физической модели – ДУ или СДУ с н. у. Аналитическое решение очень громоздко и, скорее всего не возможно. Поэтому численные методы решения – метод Эйлера или Эйлера – Кромера. Компьютерное моделирование предполагает разработку алгоритма и написание программ. Сравнение результатов (оценка погрешностей) в процессе вычислений.
На примере моделирования падения тел в воздухе рассмотрим схему: • • • Физическая модель предполагает, например, что тело – материальная точка (форма не важна, понятно, что есть модели, где форма важна и даже очень!), сила сопротивления воздуха пропорциональна, например, квадрату скорости, коэффициент сопротивления должен быть известен, ускорение свободного падения не зависит от широты и равно g≈9. 8 m/c 2. Выполняются законы нерелятивистской механики. И т. п. Математическая модель физической модели – ДУ или СДУ с н. у. Аналитическое решение очень громоздко и, скорее всего не возможно. Поэтому численные методы решения – метод Эйлера или Эйлера – Кромера. Компьютерное моделирование предполагает разработку алгоритма и написание программ. Сравнение результатов (оценка погрешностей) в процессе вычислений.
 Устойчивость и точность алгоритмов • Численные алгоритмы – алгоритм Эйлера, Эйлера Кромера для численного решения ДУ, СДУ. ДУ заменяется его разностным аналогом. В общем случае отклонение от точного решения обусловлено двумя причинами: • компьютер не оперирует с вещественными числами бесконечной точности. • Арифметические операции с ними приводят к дополнительной погрешности • (погрешность округления), которая накапливается по мере роста объема вычислений. • погрешности самого алгоритма (погрешность приближения).
Устойчивость и точность алгоритмов • Численные алгоритмы – алгоритм Эйлера, Эйлера Кромера для численного решения ДУ, СДУ. ДУ заменяется его разностным аналогом. В общем случае отклонение от точного решения обусловлено двумя причинами: • компьютер не оперирует с вещественными числами бесконечной точности. • Арифметические операции с ними приводят к дополнительной погрешности • (погрешность округления), которая накапливается по мере роста объема вычислений. • погрешности самого алгоритма (погрешность приближения).
 Сравним алгоритмы Эйлера и Эйлера – Кромера. Покажем, что второй – более точный. • Пусть дана задача Коши для ОДУ первого порядка.
Сравним алгоритмы Эйлера и Эйлера – Кромера. Покажем, что второй – более точный. • Пусть дана задача Коши для ОДУ первого порядка.
 Сравним алгоритмы Эйлера и Эйлера – Кромера. Покажем, что второй – более точный. • Пусть дана задача Коши для ОДУ первого порядка.
Сравним алгоритмы Эйлера и Эйлера – Кромера. Покажем, что второй – более точный. • Пусть дана задача Коши для ОДУ первого порядка.
 Метод Эйлера использует на каждом интервале, на которые разбивают отрезок, формулу Тейлора:
Метод Эйлера использует на каждом интервале, на которые разбивают отрезок, формулу Тейлора:
 Разобьем отрезок на n- равных длиной отрезков
Разобьем отрезок на n- равных длиной отрезков
 Значение y’ берем в левых точках отрезков • y’(xk) для всех • Тогда • Погрешность приближения или ошибка
Значение y’ берем в левых точках отрезков • y’(xk) для всех • Тогда • Погрешность приближения или ошибка
 Модификация метода Эйлера – метод Эйлера – Кромера • Значение y’ берем в правых точках отрезков
Модификация метода Эйлера – метод Эйлера – Кромера • Значение y’ берем в правых точках отрезков
 Погрешность приближения в методе Эйлера – Кромера
Погрешность приближения в методе Эйлера – Кромера
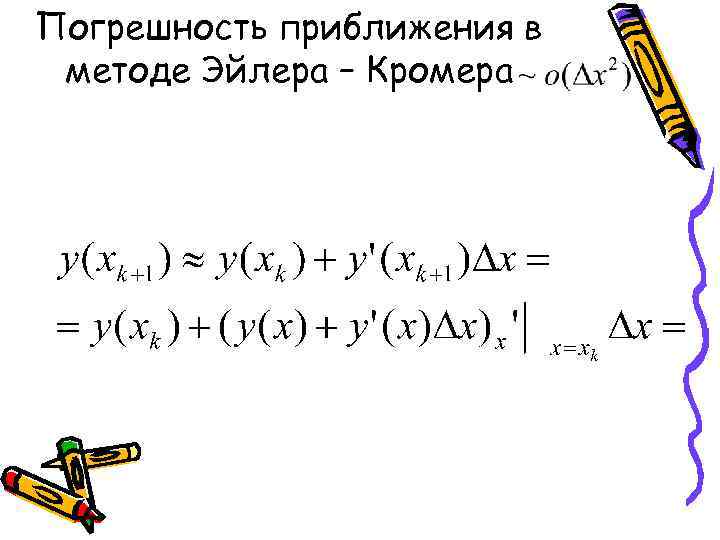 Погрешность приближения в методе Эйлера – Кромера
Погрешность приближения в методе Эйлера – Кромера
 Погрешность приближения в методе Эйлера – Кромера
Погрешность приближения в методе Эйлера – Кромера
 Погрешность приближения в методе Эйлера – Кромера
Погрешность приближения в методе Эйлера – Кромера
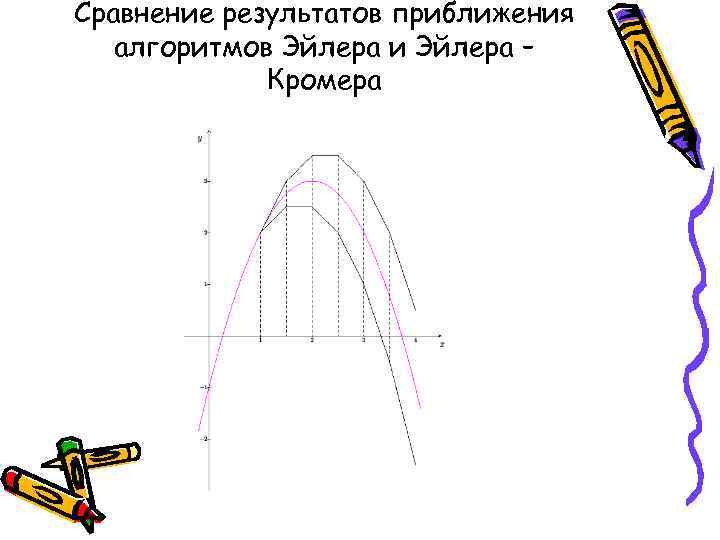 Сравнение результатов приближения алгоритмов Эйлера и Эйлера – Кромера
Сравнение результатов приближения алгоритмов Эйлера и Эйлера – Кромера
 • Практически точность решения определяют, уменьшая величину шага до тех пор, пока численное решение не перестанет зависеть от шага при требуемом уровне точности. Величина шага не должна быть очень малой, т. к. в этом случае увеличивается число шагов и возрастает машинное время и погрешность округления. • Устойчивость алгоритма определяется соответствием численных результатов истинным, может быть, что при больших значениях «времени» происходит отклонение от истины. Например, перестают выполняться законы сохранения энергии и т. д.
• Практически точность решения определяют, уменьшая величину шага до тех пор, пока численное решение не перестанет зависеть от шага при требуемом уровне точности. Величина шага не должна быть очень малой, т. к. в этом случае увеличивается число шагов и возрастает машинное время и погрешность округления. • Устойчивость алгоритма определяется соответствием численных результатов истинным, может быть, что при больших значениях «времени» происходит отклонение от истины. Например, перестают выполняться законы сохранения энергии и т. д.
 В дальнейшем рассмотрим • 1. Моделирование движения материальной точки (динамика систем, состоящих из нескольких частиц, материальных точек, тел). • 2. Метод молекулярной динамики в системе многих частиц. Моделирование газов, классических жидкостей и твердых тел. Рассмотрим «небольшие» системы многих частиц (сотни, тысячи – ограничено возможностями компьютера). Несмотря на такое «небольшое» количество частиц, он много дает для понимания наблюдаемых свойств газа, жидкости и твердого тела. • 3. Моделирование поведения систем большого числа частиц методом случайных блужданий с обработкой математической модели методом Монте Карло. Рассматриваются нелинейные задачи, случайные процессы, применяются теория вероятностей, статистика. Детальное знание траектории 104 - 1025 частиц ничего не даст, если не учитывать статистическую механику
В дальнейшем рассмотрим • 1. Моделирование движения материальной точки (динамика систем, состоящих из нескольких частиц, материальных точек, тел). • 2. Метод молекулярной динамики в системе многих частиц. Моделирование газов, классических жидкостей и твердых тел. Рассмотрим «небольшие» системы многих частиц (сотни, тысячи – ограничено возможностями компьютера). Несмотря на такое «небольшое» количество частиц, он много дает для понимания наблюдаемых свойств газа, жидкости и твердого тела. • 3. Моделирование поведения систем большого числа частиц методом случайных блужданий с обработкой математической модели методом Монте Карло. Рассматриваются нелинейные задачи, случайные процессы, применяются теория вероятностей, статистика. Детальное знание траектории 104 - 1025 частиц ничего не даст, если не учитывать статистическую механику
 Рассмотрим несколько примеров визуализации результатов компьютерного моделирования (в дальнейшем вы должны получить результаты не хуже!) Моделирование движения тела, брошенного под углом к горизонту с учетом сопротивления воздуха
Рассмотрим несколько примеров визуализации результатов компьютерного моделирования (в дальнейшем вы должны получить результаты не хуже!) Моделирование движения тела, брошенного под углом к горизонту с учетом сопротивления воздуха
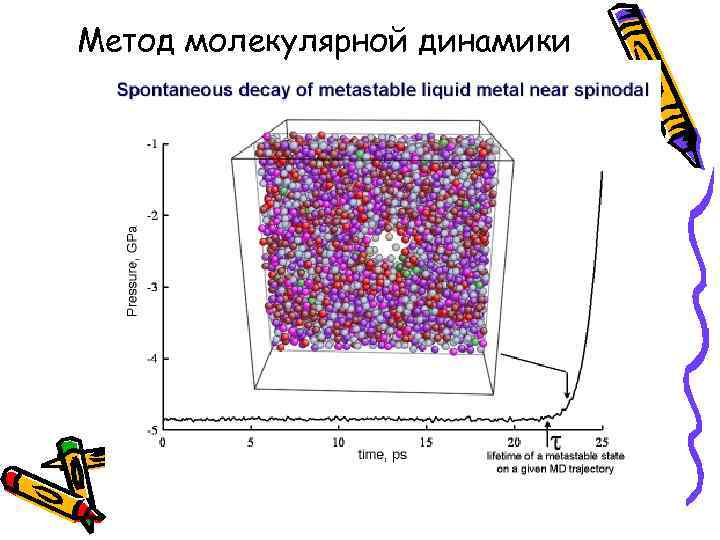 Метод молекулярной динамики
Метод молекулярной динамики
 Spontaneous decay of metastable liquid metal near spinodal
Spontaneous decay of metastable liquid metal near spinodal
 Задача Промоделируйте методом Монте-Карло непрерывное случайное блуждание свободной частицы. Напишите программу для вычисления методом Монте-Карло Pn(r)dr – вероятности того, что частица окажется в интервале координат от r до r+dr, где r означает расстояние от начала координат через N шагов. Покажите, что для достаточно большого числа шагов его можно аппроксимировать гауссовым распределением. Хорошо ли Гауссово распределение аппроксимирует функцию PN(x) для малых значений N?
Задача Промоделируйте методом Монте-Карло непрерывное случайное блуждание свободной частицы. Напишите программу для вычисления методом Монте-Карло Pn(r)dr – вероятности того, что частица окажется в интервале координат от r до r+dr, где r означает расстояние от начала координат через N шагов. Покажите, что для достаточно большого числа шагов его можно аппроксимировать гауссовым распределением. Хорошо ли Гауссово распределение аппроксимирует функцию PN(x) для малых значений N?
 Моделирование движений материальной точки Для вычисления траектории движения необходимо решить систему уравнений
Моделирование движений материальной точки Для вычисления траектории движения необходимо решить систему уравнений
 Заменим векторные уравнения на уравнения их проекций на координатные оси
Заменим векторные уравнения на уравнения их проекций на координатные оси
 Для однозначного решения шести ДУ требуется 6 н. у. • В общем случае сложная функция координат, скорости и времени, вследствие чего лишь в редких случаях можно аналитически решить систему(1), (2). Приходится использовать численные методы. Нужны все 6 условий. Все уравнения системы (2) однотипны и можно каждое решать методом Эйлера или Эйлера – Кромера
Для однозначного решения шести ДУ требуется 6 н. у. • В общем случае сложная функция координат, скорости и времени, вследствие чего лишь в редких случаях можно аналитически решить систему(1), (2). Приходится использовать численные методы. Нужны все 6 условий. Все уравнения системы (2) однотипны и можно каждое решать методом Эйлера или Эйлера – Кромера
 Процедура вычисления выглядит следующим образом: • по известным значениям x 0 и v 0 в момент времени t 0 находят в момент t 1; • затем по известным значениям v 0 и f 0 находят скорость ; • далее повторяется процедура: по известным x 1 и v 1 находят • и т. д.
Процедура вычисления выглядит следующим образом: • по известным значениям x 0 и v 0 в момент времени t 0 находят в момент t 1; • затем по известным значениям v 0 и f 0 находят скорость ; • далее повторяется процедура: по известным x 1 и v 1 находят • и т. д.
 Как провести проверку точности вычислительной схемы? Можно применять следующие методы: • • • Уменьшение шага расчета. При достаточной точности вид траектории не должен меняться. Сравнение с аналитическим решением. Проверка выполнения законов сохранения (например, энергии, импульса).
Как провести проверку точности вычислительной схемы? Можно применять следующие методы: • • • Уменьшение шага расчета. При достаточной точности вид траектории не должен меняться. Сравнение с аналитическим решением. Проверка выполнения законов сохранения (например, энергии, импульса).
 Рассмотрим одномерное и двумерное движение – падение тел и движение тел, брошенных под углом к горизонту. • Падение тел • Сразу рассмотрим математическую модель, предполагая, что физическая модель для вас очевидна. От систем (1), (2) останется два уравнения
Рассмотрим одномерное и двумерное движение – падение тел и движение тел, брошенных под углом к горизонту. • Падение тел • Сразу рассмотрим математическую модель, предполагая, что физическая модель для вас очевидна. От систем (1), (2) останется два уравнения
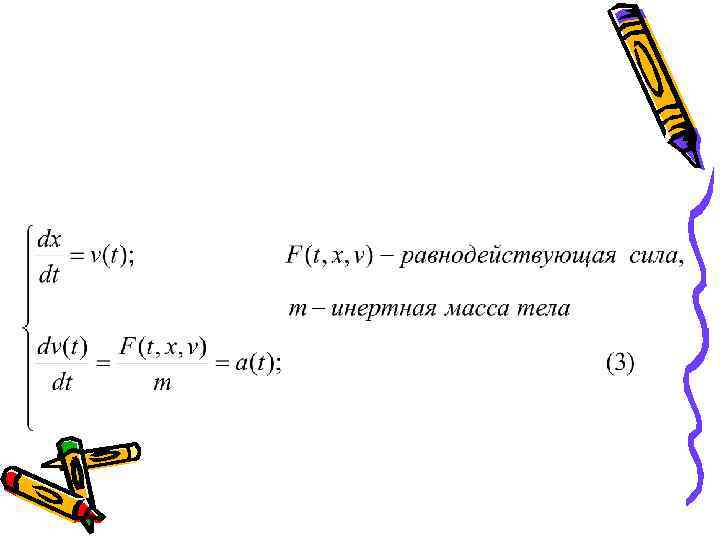
 Данная система эквивалентна одному ДУ
Данная система эквивалентна одному ДУ
 Свободное падение тел • В отсутствии сопротивления воздуха все тела, независимо от массы, размеров и состава на одинаковом расстоянии от поверхности Земли, имеют одинаковое ускорение (g). • Тогда уравнение (4) имеет вид
Свободное падение тел • В отсутствии сопротивления воздуха все тела, независимо от массы, размеров и состава на одинаковом расстоянии от поверхности Земли, имеют одинаковое ускорение (g). • Тогда уравнение (4) имеет вид
 Решение ДУ приводит к известным формулам падения тел • Предлагаю самостоятельно их получить.
Решение ДУ приводит к известным формулам падения тел • Предлагаю самостоятельно их получить.
 Законы падения тел без учета сопротивления воздуха и зависимости силы тяжести от расстояния до центра Земли
Законы падения тел без учета сопротивления воздуха и зависимости силы тяжести от расстояния до центра Земли
 Описание падения тел с учетом зависимости силы тяжести от расстояния до центра Земли • Ускорение не будет константой, если учесть, что сила тяготения
Описание падения тел с учетом зависимости силы тяжести от расстояния до центра Земли • Ускорение не будет константой, если учесть, что сила тяготения
 Описание падения тел с учетом зависимости силы тяжести от расстояния до центра Земли • Ускорение не будет константой, если учесть, что сила тяготения
Описание падения тел с учетом зависимости силы тяжести от расстояния до центра Земли • Ускорение не будет константой, если учесть, что сила тяготения
 • G – постоянная всемирного тяготения, G=6. 67*10 -11 м 3/кг*с2; • R – радиус Земли, R=6. 37*106 м • M – масса Земли, M=5. 97*1024 кг.
• G – постоянная всемирного тяготения, G=6. 67*10 -11 м 3/кг*с2; • R – радиус Земли, R=6. 37*106 м • M – масса Земли, M=5. 97*1024 кг.
 Тогда система (3) имеет вид: Это нелинейная система уравнений, ее можно решать методом Эйлера или Эйлера - Кромера.
Тогда система (3) имеет вид: Это нелинейная система уравнений, ее можно решать методом Эйлера или Эйлера - Кромера.
 Падение тел с учетом сопротивления воздуха • Рассмотрим падение тел в воздухе, предполагая что сила сопротивления воздуха пропорциональна скорости либо квадрату скорости движения. В одномерном случае при направлении вертикальной оси вниз
Падение тел с учетом сопротивления воздуха • Рассмотрим падение тел в воздухе, предполагая что сила сопротивления воздуха пропорциональна скорости либо квадрату скорости движения. В одномерном случае при направлении вертикальной оси вниз
 • Выразим константу через предельную скорость падения тела в воздухе, когда уравновешиваются силы сопротивления и сила тяжести и т. е. тело движется равномерно. Тогда
• Выразим константу через предельную скорость падения тела в воздухе, когда уравновешиваются силы сопротивления и сила тяжести и т. е. тело движется равномерно. Тогда
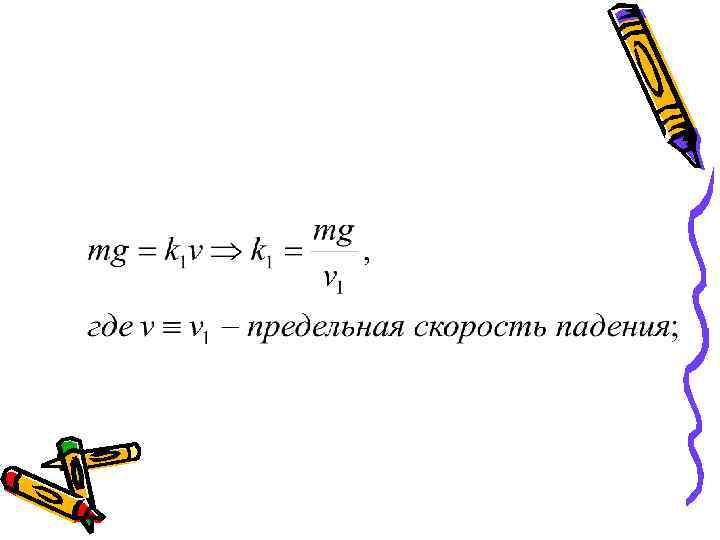
 Тогда закон движения тела до того момента, когда на тело будет действовать нулевая результирующая сила Видно, что при достижении предельногозначения скорости скобка обращается в 0 и сила равна 0.
Тогда закон движения тела до того момента, когда на тело будет действовать нулевая результирующая сила Видно, что при достижении предельногозначения скорости скобка обращается в 0 и сила равна 0.
 • Рассмотрим аналогичную ситуацию в случае силы сопротивления, пропорциональной квадрату скорости.
• Рассмотрим аналогичную ситуацию в случае силы сопротивления, пропорциональной квадрату скорости.
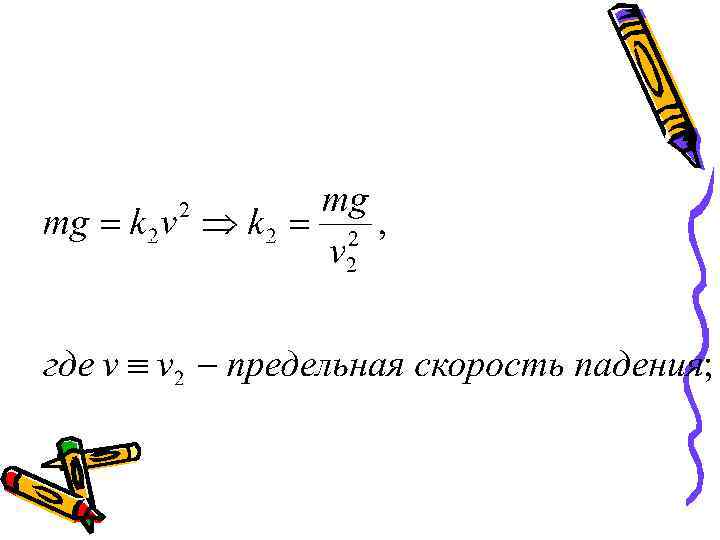
 Тогда закон движения тела до того момента, когда на тело будет действовать нулевая результирующая сила
Тогда закон движения тела до того момента, когда на тело будет действовать нулевая результирующая сила
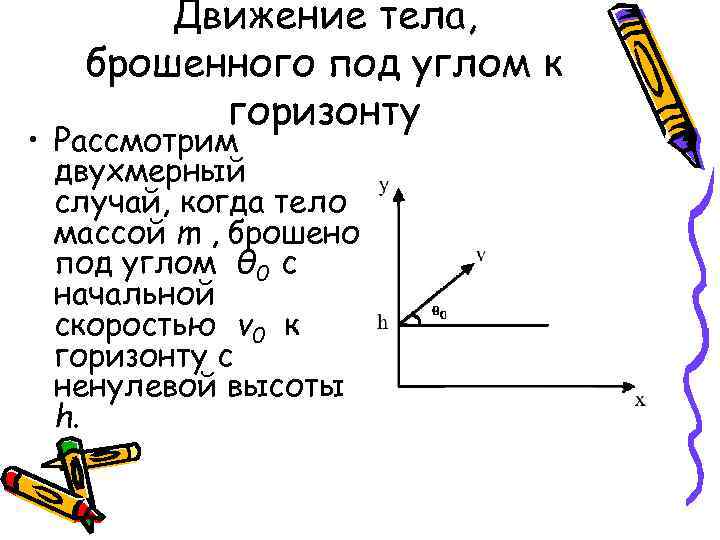 Движение тела, брошенного под углом к горизонту • Рассмотрим двухмерный случай, когда тело массой m , брошено под углом θ 0 с начальной скоростью v 0 к горизонту с ненулевой высоты h.
Движение тела, брошенного под углом к горизонту • Рассмотрим двухмерный случай, когда тело массой m , брошено под углом θ 0 с начальной скоростью v 0 к горизонту с ненулевой высоты h.
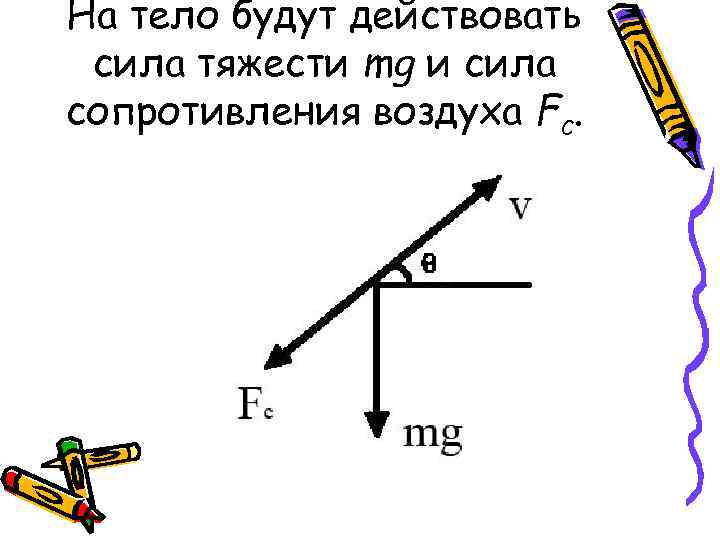 На тело будут действовать сила тяжести mg и сила сопротивления воздуха Fc.
На тело будут действовать сила тяжести mg и сила сопротивления воздуха Fc.
 Система уравнений движения Ньютона для компонент x и y
Система уравнений движения Ньютона для компонент x и y
 Предполагая, что сила сопротивления воздуха пропорциональна скорости либо квадрату скорости движения.
Предполагая, что сила сопротивления воздуха пропорциональна скорости либо квадрату скорости движения.
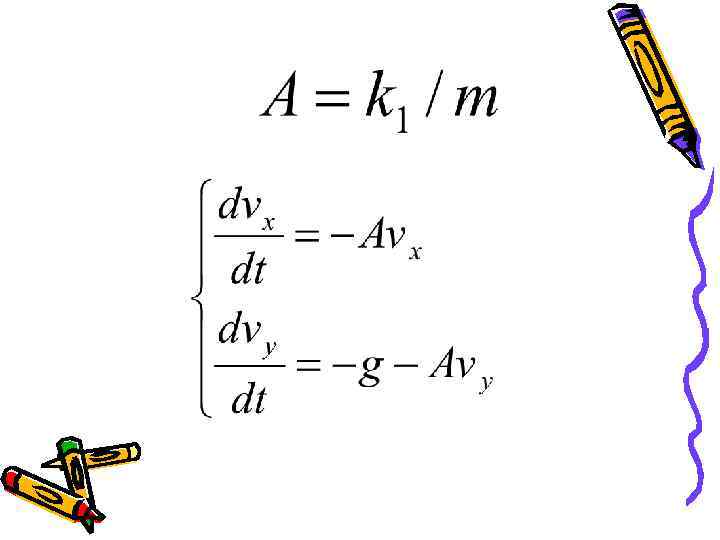
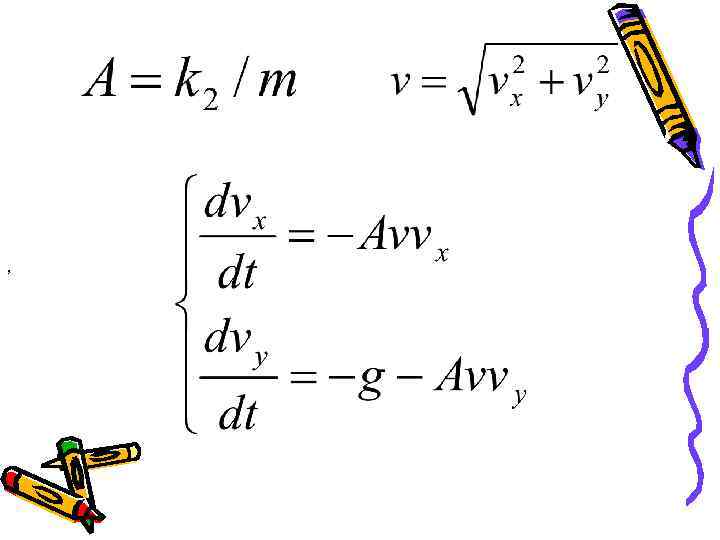 ,
,
 С учетом зависимости силы тяжести от расстояния до цента Земли: если
С учетом зависимости силы тяжести от расстояния до цента Земли: если
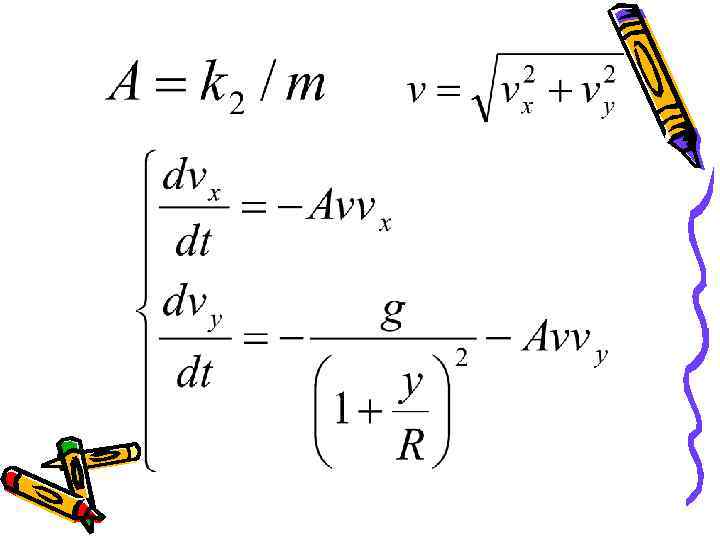
 Домашнее задание • • • Описать падение тела, если сила сопротивления пропорциональна скорости и без учета сопротивления воздуха. Сравнить результаты аналитических и приближенных (компьютерных) расчетов. Движение тела, брошенного под углом к горизонту с учетом сопротивления воздуха. Задача о прыжке парашютиста. Филиппов, № 88.
Домашнее задание • • • Описать падение тела, если сила сопротивления пропорциональна скорости и без учета сопротивления воздуха. Сравнить результаты аналитических и приближенных (компьютерных) расчетов. Движение тела, брошенного под углом к горизонту с учетом сопротивления воздуха. Задача о прыжке парашютиста. Филиппов, № 88.
 Филиппов, № 88. • Парашютист прыгнул с высоты 1. 5 км, а раскрыл парашют на высоте 0. 5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50 м/с. Изменением плотности с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.
Филиппов, № 88. • Парашютист прыгнул с высоты 1. 5 км, а раскрыл парашют на высоте 0. 5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50 м/с. Изменением плотности с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.
 • Решить задачу аналитически и численно, используя метод Эйлера, а затем метод Эйлера-Кромера. Сравнить результаты. Построить графики S(t), v(t), a(t)
• Решить задачу аналитически и численно, используя метод Эйлера, а затем метод Эйлера-Кромера. Сравнить результаты. Построить графики S(t), v(t), a(t)
 Методом Эйлера
Методом Эйлера
 Методом Эйлера-Кромера
Методом Эйлера-Кромера
 Литература • • • Гулд, Тобочник «Компьютерное моделирование в физике» , т. 1 и 2. Мельников Ю. Б. Математическое моделирование: структура, алгебра моделей, обучение построению математических моделей: Монография. Екатеринбург: Уральское издательство, 2004, 384 с. Куксин А. Ю. , Норман Г. Э. , Стегайлов В. В. Фазовая диаграмма и спинодальный распад метастабильных состояний Леннард-Джонсовской системы // Теплофизика Высоких Температур. 2007. Т. 45. N. 1. С. 43– 55.
Литература • • • Гулд, Тобочник «Компьютерное моделирование в физике» , т. 1 и 2. Мельников Ю. Б. Математическое моделирование: структура, алгебра моделей, обучение построению математических моделей: Монография. Екатеринбург: Уральское издательство, 2004, 384 с. Куксин А. Ю. , Норман Г. Э. , Стегайлов В. В. Фазовая диаграмма и спинодальный распад метастабильных состояний Леннард-Джонсовской системы // Теплофизика Высоких Температур. 2007. Т. 45. N. 1. С. 43– 55.


