SCH-T-3.ppt
- Количество слайдов: 40

Компьютерная Схемотехника 2012 БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ n-МОП И КМОП ЛОГИЧЕСКИЕ КОМБИНАЦИОННЫЕ СХЕМЫ ХНУРЭ, факультет КИУ, каф ЭВМ, Тел. 70 -21 -354. Доц. Торба А. А.

Компьютерная Схемотехника 2012 ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИ • БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ n-МОП • ЭЛЕКТРОННЫЙ КЛЮЧ КМОП • ЛОГИЧЕСКИЕ КОМБИНАЦИОННЫЕ СХЕМЫ • СУММАТОРЫ • СОСТЯЗАНИЯ СХЕМАХ (ГОНКИ) В ЛОГИЧЕСКИХ • ПРЕОБРАЗОВАТЕЛИ ТОРЫ КОДОВ, • МУЛЬТИПЛЕКСОРЫ И ДЕШИФРА- ДЕМУЛЬТИПЛЕК-

БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ n-МОП В последнее время большое распространение получают логические ИС на полевых транзисторах. Управление полевым транзистором осуществляется не током, как в биполярном транзисторе, а напряжением, т. е. электрическим полем, приложенным между входным электродом - ЗАТВОРОМ - и основной массой полупроводниковой пластины (называемой ПОДЛОЖКОЙ), в которой реализован КАНАЛ прохождения тока от электрода ИСТОК к электроду СТОК. исток затвор окисел канал (n-типа) сток подложка (р-типа) с з п и

В большинстве схем подложка электрически соединяется с истоком. Поэтому можно говорить, что входное напряжение подается между затвором и истоком. Существует некоторая аналогия в работе биполярного и полевого транзистора. Затвор играет роль управляющего электрода (как в биполярном транзисторе - база). Роль истока аналогична эмиттеру, а со стока снимается выходное напряжение (как с коллектора у биполярного транзистора). +Е R Uвх з Uвых с и Сн На рис. приведена схема простейшего электронного ключа на полевом транзисторе с каналом проводимости n-типа по схеме с общим истоком. Питающее напряжение (+Е) положительной полярности приложено к стоку через резистор нагрузки R.

Металлический затвор изолирован от канала тонкой изоляционной пленкой окиси кремния. Ток во входной цепи не течет. Поэтому основной статической характеристикой такого ключа является передаточная характеристика. ∆Uвх Uвых U 1 вых=+Е А С В 0 ∆Uвых U 0 вых +Е Uвх U′ Uпор U″ При нулевом входном напряжении (Uвх=0) канал имеет очень большое сопротивление и на выход ключа подается напряжение питания через резистор R. Выходное напряжение логической единицы (U 1 вых) равно напряжению питания +Е.

При увеличении входного напряжения выше U' сопротивление канала постепенно уменьшается и на выход подается часть напряжения источника питания с делителя, образованного сопротивлением канала и резистором R (участок А-В). Сопротивление канала не может уменьшиться до нуля. При входном напряжении выше U" сопротивление канала достигает минимальной величины, и дальнейшее увеличение входного напряжения не влияет на сопротивление канала. Величины U', U" и Rкмин определяются технологическими параметрами: степенью легирования канала, степенью шероховатости поверхности канала, геометрическими размерами канала; а также напряжением питания электронного ключа. На участке А-В, т. е. при входном напряжении от U' до U" электронный ключ работает как аналоговый усилитель с коэффициентом усиления Ku=∆Uвых/∆Uвх.

Точка пересечения передаточной характеристики с биссектрисой первого квадранта (точка С) определяет пороговое напряжение Uпор электронного ключа. Переходные процессы в электронных ключах на полевых транзисторах определяются временем перезаряда паразитного конденсатора нагрузки Сн через сопротивление открытого канала Rкмин или через резистор R (который на порядок больше) при закрытом канале. Поэтому быстродействие таких логических схем относительно невелико при средних уровнях потребляемой мощности на один ключ. Единственное преимущество логических ключей на n. МОП структурах - минимальные габариты. При ограниченной площади кремниевой пластины на ее поверхности можно разместить максимальное количество таких логических элементов.

Электронный ключ КМОП Значительно лучшими параметрами обладают электронные ключи, выполненные на полевых транзисторах с взаимно дополняющей проводимостью n- и p-типа. Этим объясняется название ключей - КМОП (буква К - от слова комплиментарный, дополнительный). Электронный ключ на полевом транзисторе с каналом n-типа +Е з и VT 1 в качестве нагрузки имеет VT 2 полевой транзистор VT 2 с с Uвых каналом p-типа. Поскольку Uвх схема симметричная, то можно з с говорить, что ключ на транзис. VT 1 Сн и торе p-типа VT 2 в качестве нагрузки имеет полевой транзистор с каналом n-типа VT 1.
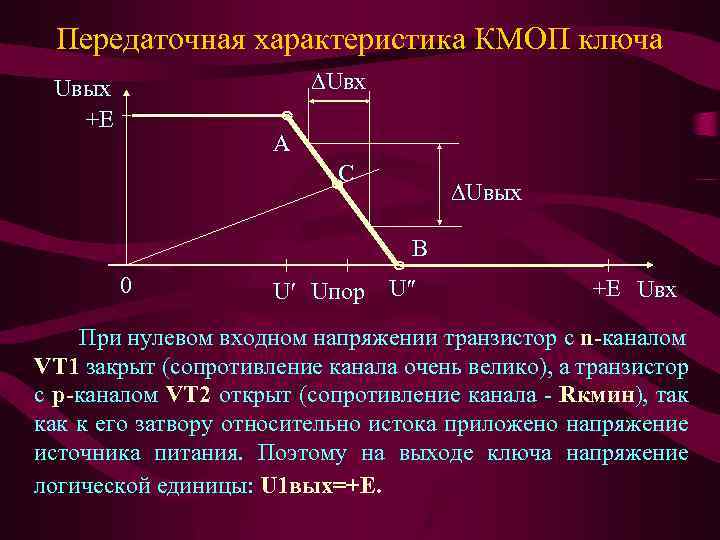
Передаточная характеристика КМОП ключа ∆Uвх Uвых +Е А С ∆Uвых В 0 U′ Uпор U″ +Е Uвх При нулевом входном напряжении транзистор с n-каналом VT 1 закрыт (сопротивление канала очень велико), а транзистор с р-каналом VT 2 открыт (сопротивление канала - Rкмин), так к его затвору относительно истока приложено напряжение источника питания. Поэтому на выходе ключа напряжение логической единицы: U 1 вых=+Е.

При увеличении входного напряжения выше U' (точка А) начинает уменьшаться сопротивление канала транзистора VT 1, а сопротивление канала VT 2 - увеличивается. Выходное напряжение постепенно уменьшается и в конце участка А-В практически доходит до нуля (U 0 вых=0) при полном закрывании транзистора VT 2 и уменьшении сопротивления канала транзистора VT 1 до величины Rкмин. На участке А-В оба транзистора работают в активном режиме усиления аналогового сигнала с коэффициентом усиления по напряжению: Ku=∆Uвых/∆Uвх. При этом оба канала имеют конечное сопротивление и через два транзистора течет сквозной ток от источника питания. С увеличением входного напряжения выше U" канал транзистора VT 2 закрывается и ток через КМОП ключ от источника питания не протекает.

Таким образом, при входном напряжении ниже U' а также выше U" через КМОП ключ ток от источника питания практически не течет. Статическая потребляемая мощность близка к нулю. Пороговое напряжение Uпор определяется как точка пересечения передаточной характеристики с биссектрисой первого квадранта (точка С). Пороговое напряжение почти равно половине напряжения источника питания. Участок с напряжением U'-U" примерно равен 10. . 20% от напряжения источника питания, но имеет технологический разброс относительно середины напряжения источника питания. Поэтому входное напряжение низкого логического уровня U 0 вх должно быть менее 1/3 напряжения источника питания, а входное напряжение высокого логического уровня U 1 вх должно быть более 2/3 напряжения питания. Абсолютное значение напряжения источника питания +Е может изменяться в широких пределах. Это позволяет питать КМОП логические схемы от нестабилизированного источника питания, что значительно упрощает и удешевляет источник питания.

Переходные процессы в КМОП ключах определяются временем перезаряда паразитного конденсатора Сн через открытые каналы транзисторов. Поэтому времена запаздывания КМОП ключей значительно меньше, чем у n-МОП логических элементов. Большим преимуществом КМОП логических элементов является минимальная потребляемая мощность в статическом режиме. Однако с ростом частоты переключения потребляемая мощность пропорционально увеличивается, потому что при каждой смене логического состояния происходит перезаряд паразитных конденсаторов токами, потребляемыми от источника питания, а также через оба транзистора протекает короткий импульс сквозного тока. При максимальной частоте переключения потребляемая мощность КМОП элементов соизмерима с потребляемой мощностью ТТЛШ микросхем.
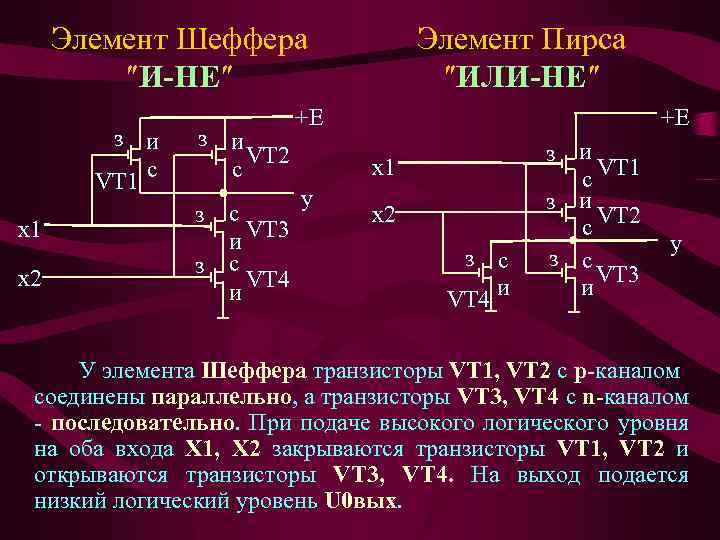
Элемент Шеффера ″И-НЕ″ з и с VT 1 x 2 з и VT 2 с з з с VT 3 и с VT 4 и Элемент Пирса ″ИЛИ-НЕ″ +Е +Е x 1 y x 2 з с VT 4 и з и с VT 1 з и с VT 2 з с VT 3 и y У элемента Шеффера транзисторы VT 1, VT 2 с р-каналом соединены параллельно, а транзисторы VT 3, VT 4 с n-каналом - последовательно. При подаче высокого логического уровня на оба входа Х 1, Х 2 закрываются транзисторы VT 1, VT 2 и открываются транзисторы VT 3, VT 4. На выход подается низкий логический уровень U 0 вых.

Если на одном из входов присутствует низкий логический уровень (например, на входе Х 1), то транзистор VT 3 будет закрыт, а на выход элемента «И-НЕ» через открытый транзистор VT 1 подается высокий логический уровень U 1 вых, равный напряжению источника питания. Схема элемента Пирса симметрична схеме элемента Шеффера, что наглядно иллюстрирует симметрию правила де. Моргана. У элемента «ИЛИ-НЕ» транзисторы с р-каналом VT 1, VT 2 соединены последовательно, а n-канальные транзисторы VT 3, VT 4 - параллельно. У КМОП элементов недопустимо оставлять свободными входы логических элементов, т. к. их состояние входа будет неопределенным, может легко изменяться под действием наводимых помех, а также может привести к заметному увеличению потребляемого тока от источника питания через два полуоткрытых транзистора. Недопустимо также объединение выходов нескольких логических элементов. При этом через открытые каналы полевых транзисторов протекают большие сквозные токи, а состояние выходов будет неопределенным.

Любые более сложные логические схемы могут быть синтезированы на основе базовых элементов «И-НЕ» , «ИЛИНЕ» и инверторов. Особый интерес представляет схема КОММУТАТОРА. В этой схеме между входом «Х» и выходом «Y» включены параллельно два полевых транзистора: VT 3 с р-каналом и VT 4 с n-каналом. При нулевом напряжении на входе управления «#» оба +Е транзистора VT 3, VT 4 заз и Y крыты (т. е. между входом «X» VT 2 з и з c и выходом «Y» существует с VT 4 очень большое сопротив. VT 3 с з и ление). Управляющее напря# VT 1 с жение на р-канальный и Х транзистор VT 3 подается через КМОП инвертор (на транзисторах VT 1, VT 2).

Если на управляющий вход «#» подано напряжение высокого логического уровня, оба транзистора VT 3 и VT 4 открываются. При этом вход «Х» соединен с выходом «Y» малым сопротивлением открытых каналов полевых транзисторов. Наличие двух транзисторов разной проводимости выравнивает сопротивления для прямого и обратного протекания токов через открытый коммутатор. Понятие вход «Х» и выход «Y» чисто условные, т. к. коммутатор полностью симметричен и может быть также использован для коммутации аналоговых сигналов. Такой коммутатор может применяться как самостоятельный логический элемент, а также входит в состав микросхем, например, для организации логических элементов с третьим Z-состоянием выхода.

СХЕМОТЕХНИКА ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВ • ЛОГИЧЕСКИЕ КОМБИНАЦИОННЫЕ СХЕМЫ Логические комбинационные схемы (ЛКС) предназначены для преобразования входных логических сигналов в соответствии с заданным алгоритмом. В общем случае ЛКС имеет «m» входов и «n» выходов X 1 ЛКС X 2 X 3 Xm … Y 1 Y 2 Y 3 … Yn Входными и выходными сигналами являются логические переменные, т. е. они могут принимать только два значения – « 0» , « 1» или «низкий логический уровень» , «высокий логический уровень» . Обычно входные и выходные сигналы обозначаются любыми латинскими буквами.

Алгоритм преобразования ЛКС может быть задан тремя способами: Ø Булевыми выражениями: Ø Таблицей состояний, в которой количество строк равно количеству возможных комбинаций входных переменных (для логических переменных с двумя состояниями количество комбинаций - 2 m); первые два столбца выходных сигналов - Y 1, Y 2 - соответствуют приведенным логическим функциям; Ø Словесное описание (задание алгоритма на вербальном уровне), например: ЛКС мажоритарного элемента имеет 3 входа и 1 выход; сигнал на выходе равен « 1» , если не менее двух входных сигналов равны « 1» .
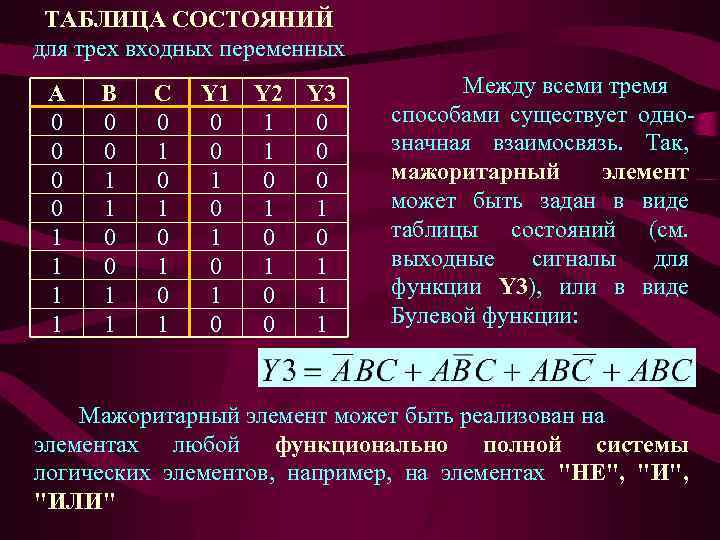
ТАБЛИЦА СОСТОЯНИЙ для трех входных переменных A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 Y 1 Y 2 Y 3 0 1 0 1 0 0 0 1 1 1 0 0 1 Между всеми тремя способами существует однозначная взаимосвязь. Так, мажоритарный элемент может быть задан в виде таблицы состояний (см. выходные сигналы для функции Y 3), или в виде Булевой функции: Мажоритарный элемент может быть реализован на элементах любой функционально полной системы логических элементов, например, на элементах "НЕ", "ИЛИ"
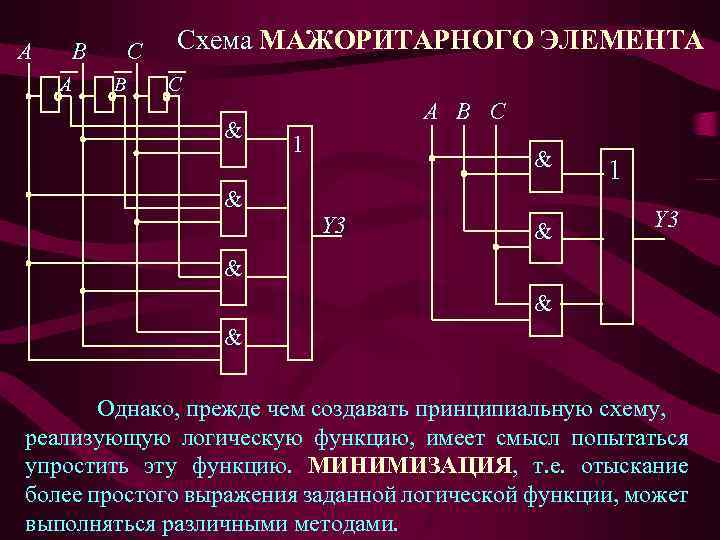
A B A C B Схема МАЖОРИТАРНОГО ЭЛЕМЕНТА C & & A В С 1 & Y 3 & 1 Y 3 & & & Однако, прежде чем создавать принципиальную схему, реализующую логическую функцию, имеет смысл попытаться упростить эту функцию. МИНИМИЗАЦИЯ, т. е. отыскание более простого выражения заданной логической функции, может выполняться различными методами.

В частности, можно, используя алгебраические преобразования исходного выражения, провести все возможные операции ПОГЛОЩЕНИЯ и СКЛЕИВАНИЯ в соответствии с законами АЛГЕБРЫ ЛОГИКИ Для функций, содержащих не более четырех переменных, удобно проводить минимизацию, пользуясь диаграммами ВЕЙЧА (картами КАРНО). Диаграмма ВЕЙЧА представляет собой прямоугольную (или квадратную) таблицу, в которой количество клеток равно количеству комбинаций входных переменных, причем соседние клетки (снизу и сверху, слева и справа) нумеруются так, чтобы изменение претерпевала только одна входная переменная. Это же правило должно выполняться и для крайних клеток, потому что диаграмма Вейча (карта Карно) представляет из себя замкнутую поверхность, а на плоскости мы рисуем развертку этой поверхности. На рис. приведены диаграммы Вейча (карты Карно) для мажоритарного элемента с тремя входными переменными.

A A, B C 00 01 11 10 0 1 0 1 1 1 C 0 0 1 0 C 0 1 1 1 В Операция склеивания : ab A В В V ab = a (b V b) = a Операциям склеивания соответствуют на карте Карно объединения соседних единиц в прямоугольники (или квадраты) с числом клеток, кратных 2 k (2, 4, 8, 16. . . ). Конечной целью минимизации является: ОБЪЕДИНЕНИЕ ВСЕХ ЕДИНИЦ В ПРЯМОУГОЛЬНИКИ С МАКСИМАЛЬНЫМИ РАЗМЕРАМИ. При этом необходимо учитывать, что в карте Карно левые и правые боковые грани соединены (т. е. диаграмма свернута в цилиндр) и возможно склеивание крайних правых клеток с крайними левыми.
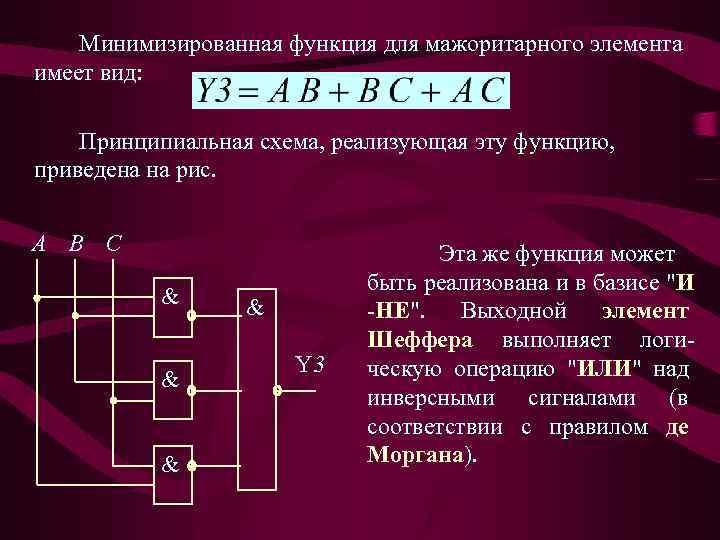
Минимизированная функция для мажоритарного элемента имеет вид: Принципиальная схема, реализующая эту функцию, приведена на рис. A B C & & Y 3 Эта же функция может быть реализована и в базисе "И -НЕ". Выходной элемент Шеффера выполняет логическую операцию "ИЛИ" над инверсными сигналами (в соответствии с правилом де Моргана).
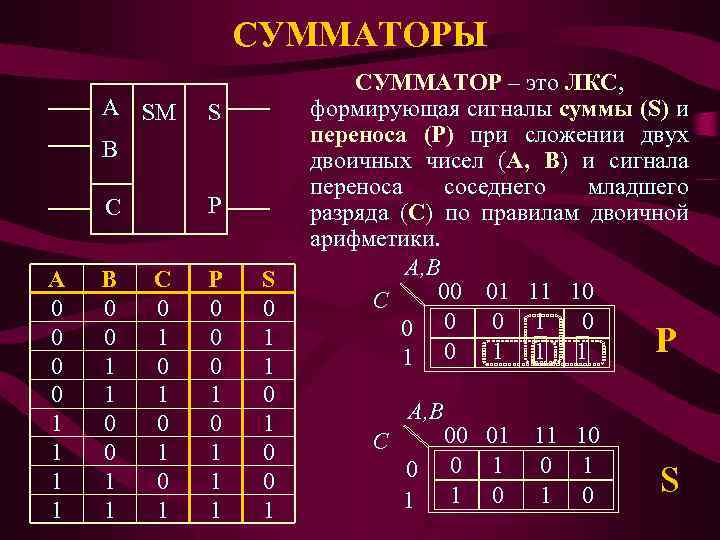
СУММАТОРЫ A SM S B P C A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 P 0 0 0 1 1 1 S 0 1 1 0 0 1 СУММАТОР – это ЛКС, формирующая сигналы суммы (S) и переноса (Р) при сложении двух двоичных чисел (А, В) и сигнала переноса соседнего младшего разряда (С) по правилам двоичной арифметики. A, B 00 01 11 10 C 0 0 1 Р 0 1 1 A, B C 0 1 00 01 0 11 10 0 1 1 0 S
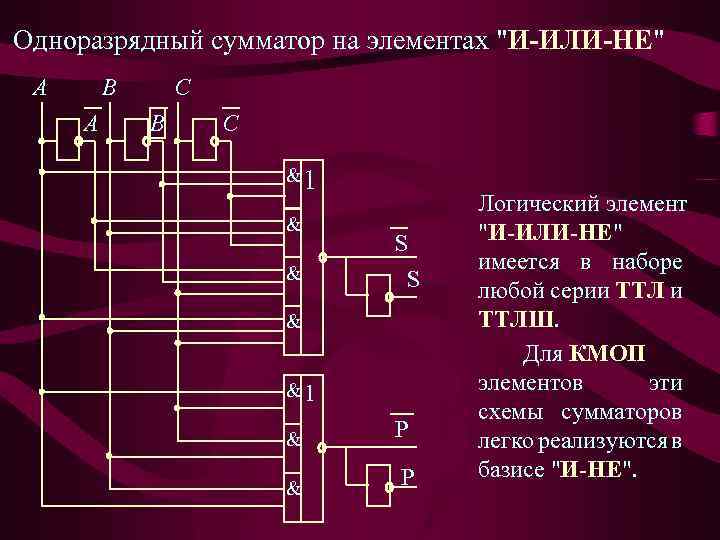
Одноразрядный сумматор на элементах "И-ИЛИ-НЕ" A B A C B C &1 & & S S & &1 & P Логический элемент "И-ИЛИ-НЕ" имеется в наборе любой серии ТТЛШ. Для КМОП элементов эти схемы сумматоров легко реализуются в базисе "И-НЕ".
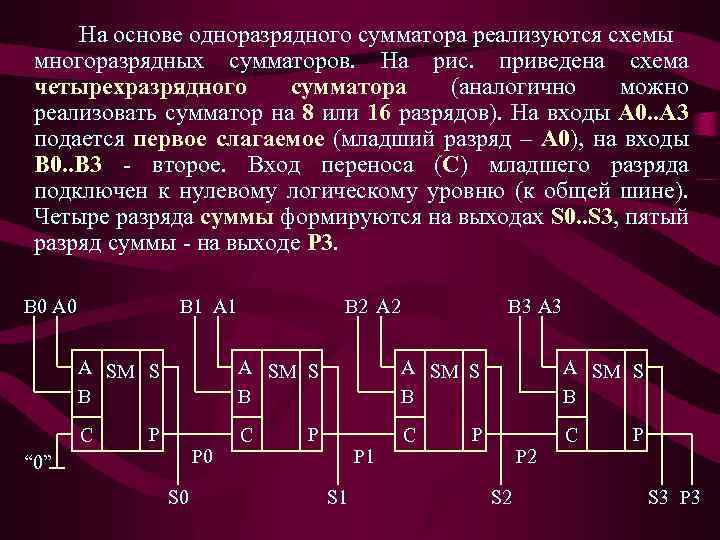
На основе одноразрядного сумматора реализуются схемы многоразрядных сумматоров. На рис. приведена схема четырехразрядного сумматора (аналогично можно реализовать сумматор на 8 или 16 разрядов). На входы А 0. . А 3 подается первое слагаемое (младший разряд – А 0), на входы В 0. . В 3 - второе. Вход переноса (С) младшего разряда подключен к нулевому логическому уровню (к общей шине). Четыре разряда суммы формируются на выходах S 0. . S 3, пятый разряд суммы - на выходе Р 3. B 0 A 0 B 1 A SM S B C B 2 A SM S B P P 0 “ 0” S 0 C B 3 A SM S B P P 1 S 1 C A SM S B P P 2 S 2 C P S 3 P 3

В формировании сигналов S 3, P 3 участвуют все входные переменные А 0. . А 3, В 0. . В 3. Но ко входам последней логической схемы эти сигналы проходят через разное количество логических элементов, что вызывает появление на выходах ложных коротких импульсов, образованных эффектом гонок (состязаний). СОСТЯЗАНИЯ (ГОНКИ) В ЛОГИЧЕСКИХ СХЕМАХ Реализация ЛКС всегда исходит из Булевой функции или таблицы состояний. На самом деле такое описание схемы является идеализацией, не учитывающей задержки распространения сигналов в реальных логических элементах. Наличие задержек приводит к тому, что в некоторые моменты времени не подтверждаются основные аксиомы алгебры логики:
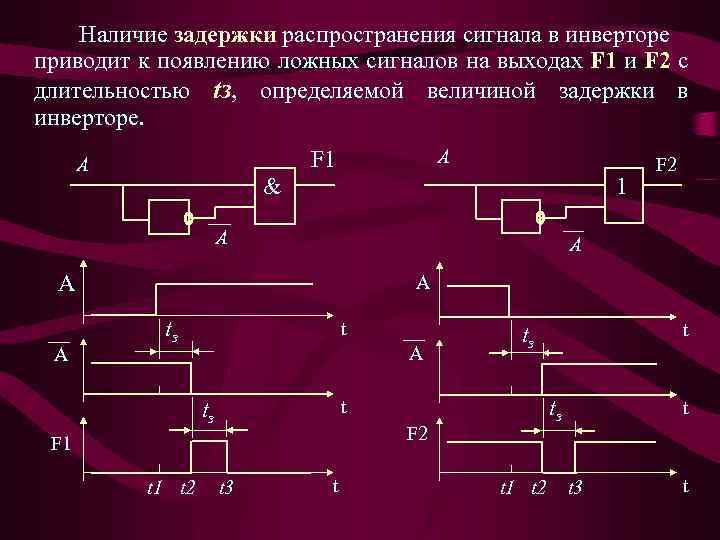
Наличие задержки распространения сигнала в инверторе приводит к появлению ложных сигналов на выходах F 1 и F 2 с длительностью tз, определяемой величиной задержки в инверторе. A F 1 A 1 & A A F 2 A tз t 1 t 2 tз t F 2 F 1 t 3 t t tз t 1 t 2 t t 3 t

Ситуации, при которых появляются ложные сигналы малой длительности, называются СОСТЯЗАНИЯМИ или ГОНКАМИ. Появление гонок связано с прохождением нескольких логических сигналов к входу одной схемы через цепи с разным количеством логических элементов. Даже, если количество элементов в этих цепях будет одинаковым, возникновение гонок возможно за счет различий времени задержки распространения сигналов внутри элементов (технологический разброс времени задержки у одинаковых элементов может достигать 1, 5. . 2 раза). Существует ДВА радикальных метода борьбы с ГОНКАМИ (состязаниями): Ø стробирование логических сигналов импульсами, подаваемыми после завершения всех переходных процессов; Ø запоминание логических сигналов в регистрах после завершения всех переходных процессов.

ПРЕОБРАЗОВАТЕЛИ КОДОВ, ДЕШИФРАТОРЫ ПРЕОБРАЗОВАТЕЛИ КОДОВ предназначены для перевода чисел из одной формы представления в другую. Например, при вводе информации в ЭВМ необходимо преобразовать десятичные числа в двоичные, а при выводе информации на индикаторы или печатающее устройство - двоичные или двоично-десятичные коды преобразовываются в коды управления знакогенератором, светодиодными или жидкокристаллическими индикаторами, механизмом печати. Отправным пунктом для построения ПРЕОБРАЗОВАТЕЛЯ КОДОВ является таблица состояний, в которой записываются полный набор входных и соответствующий набор выходных слов. Синтез ЛКС преобразователей кодов осуществляется известными алгоритмами, например, при помощи карт Карно.

Преобразователи двоичного кода в код « 1 из n» называются ДЕШИФРАТОРАМИ. Они могут использоваться как самостоятельное устройство при выводе информации из ЭВМ, а также входят в состав микросхем памяти и других микросхем для выборки одной из множества ячеек. Таблица состояний дешифратора « 1 из 8» X 2 X 1 X 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 Минимизировать логические функции для каждого выхода Yn невозможно, т. к. во всех картах Карно будет только по одной единице.
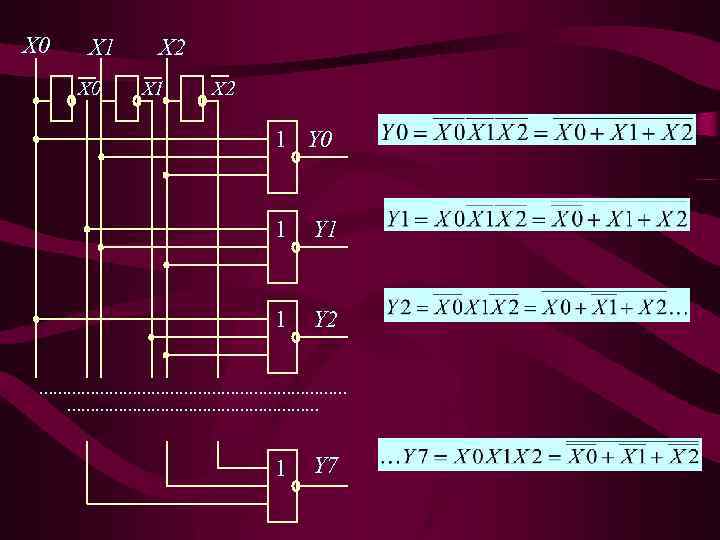
X 0 X 1 X 0 X 2 X 1 X 2 1 Y 0 1 Y 1 1 Y 2 …………………………… 1 Y 7
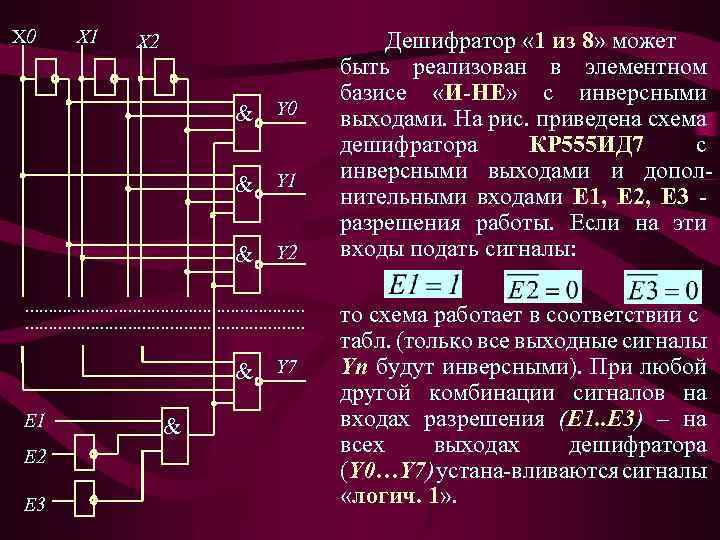
X 0 X 1 X 2 & Y 0 & Y 1 & Y 2 …………………………………………………… & Y 7 E 1 E 2 E 3 & Дешифратор « 1 из 8» может быть реализован в элементном базисе «И-НЕ» с инверсными выходами. На рис. приведена схема дешифратора КР 555 ИД 7 с инверсными выходами и дополнительными входами Е 1, Е 2, Е 3 - разрешения работы. Если на эти входы подать сигналы: то схема работает в соответствии с табл. (только все выходные сигналы Yn будут инверсными). При любой другой комбинации сигналов на входах разрешения (E 1. . E 3) – на всех выходах дешифратора (Y 0…Y 7) устана-вливаются сигналы «логич. 1» .

Дополнительные входы разрешения могут быть использованы для подачи сигналов стробирования (с целью подавления нежелательных ложных импульсов за счет «эффекта гонок» ). X 0 DC Y 0 X 1 Y 1 X 2 Y 3 Y 4 & Y 5 Y 6 E Y 7 Входы расширения можно использовать также при реализации более сложных дешифраторов, например, « 1 из 16» или « 1 из 32» и т. д. На рис. приведено условное графическое обозначение (УГО) дешифратора КР 555 ИД 7. При реализации более сложных дешифраторов, например, « 1 из 1000» или « 1 из 1000000» используют многоступенчатые схемы дешифраторов.

МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ В цифровых устройствах часто возникает задача передачи цифровой информации от «m» различных устройств к «n» приемникам через канал общего пользования. Для этого на входе канала устанавливается устройство, называемое МУЛЬТИПЛЕКСОРОМ, которое согласно коду адреса Am подключает к каналу один из источников информации, а на выходе канала устройство ДЕМУЛЬТИПЛЕКСОР обеспечивает передачу информации к приемнику, имеющему цифровой адрес An. Мультиплексор и демультиплексор включают в себя дешифратор адреса. Выходные сигналы дешифратора управляют логическими вентилями, разрешая передачу информации через один выбранный вентиль.
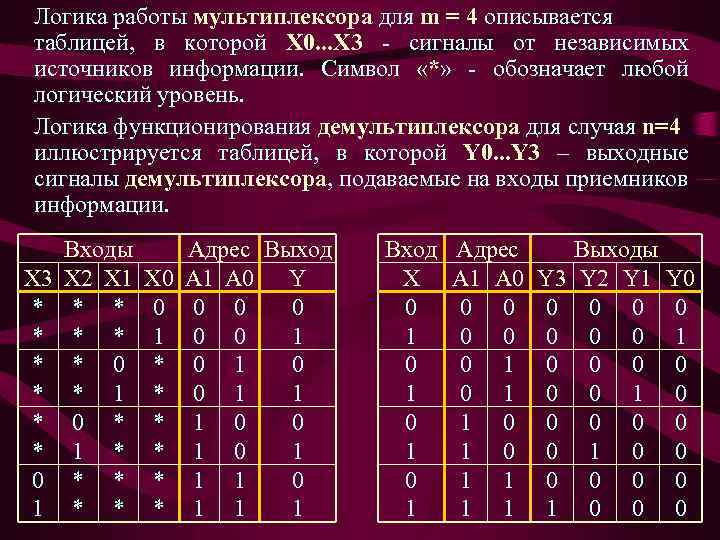
Логика работы мультиплексора для m = 4 описывается таблицей, в которой X 0. . . X 3 - сигналы от независимых источников информации. Символ «*» - обозначает любой логический уровень. Логика функционирования демультиплексора для случая n=4 иллюстрируется таблицей, в которой Y 0. . . Y 3 – выходные сигналы демультиплексора, подаваемые на входы приемников информации. X 3 * * * 0 1 Входы X 2 X 1 * * * 0 * 1 * * * X 0 0 1 * * * Адрес Выход A 1 A 0 Y 0 0 0 1 1 1 0 0 1 1 1 Вход X 0 1 0 1 Адрес A 1 A 0 0 0 1 0 1 0 1 1 Y 3 0 0 0 0 1 Выходы Y 2 Y 1 0 0 0 0 1 0 0 0 Y 0 0 1 0 0 0
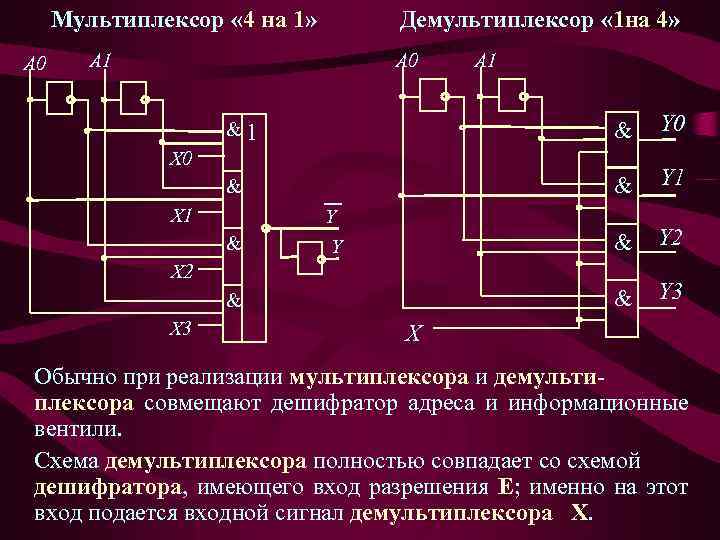
Мультиплексор « 4 на 1» A 0 Демультиплексор « 1 на 4» A 1 A 0 A 1 &1 & Y 0 & & Y 1 & Y 2 & Y 3 X 0 X 1 & Y Y X 2 & X 3 X Обычно при реализации мультиплексора и демультиплексора совмещают дешифратор адреса и информационные вентили. Схема демультиплексора полностью совпадает со схемой дешифратора, имеющего вход разрешения Е; именно на этот вход подается входной сигнал демультиплексора Х.

Вопросы для экспресс-контроля • 1. Назовите методы описания (задания) логических комбинационных схем (ЛКС). • 2. Объясните необходимость минимизации ЛКС. Назовите методы минимизации ЛКС. • 3. Назначение сумматоров. Реализация многоразрядных сумматоров. • 4. Что такое состязания (гонки) в логических элементах? • 5. Методы борьбы с гонками (состязаниями). • 6. Что такое дешифраторы? Области применения дешифраторов. Реализация дешифраторов.

Вопросы для экспресс-контроля • 7. Зачем дешифраторам необходим вход ОЕ – разрешение выхода? • 8. Назначение мультиплексоров и демультиплексоров.

ЛЕКЦИЯ ОКОНЧЕНА СПАСИБО ЗА ВНИМАНИЕ
SCH-T-3.ppt