КОМПЬЮТЕРНАЯ ЛОГИКА Раздел 1







 КОМПЬЮТЕРНАЯ ЛОГИКА Раздел 1 МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ Минимизация логических 1 функций
КОМПЬЮТЕРНАЯ ЛОГИКА Раздел 1 МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ Минимизация логических 1 функций
 https: //sites. google. com/site/komputlogika/ Минимизация логических 2 функций
https: //sites. google. com/site/komputlogika/ Минимизация логических 2 функций
 https: //sites. google. com/site/komputlogika/ Минимизация логических 3 функций
https: //sites. google. com/site/komputlogika/ Минимизация логических 3 функций
 . МИНИМАЛЬНЫЕ ДИЗЪЮНКТИВНАЯ И КОНЪЮКТИВНАЯ НОРМАЛЬНЫЕ ФОРМЫ (МДНФ И МКНФ) Определение 1: МДНФ булевой функции является дизъюнкция простых импликант. Определение 2: МКНФ булевой функции является конъюнкция простых имплициент. Определение 3: булевая функция G (x 1, …, xn) называется импликантой логической функции F (x 1, …, xn), если для любого набора переменных, на котором G (x 1, …, xn) = 1, справедливо и F (x 1, …, xn) = 1. Определение 4: булевая функция H (x 1, …, xn) называется имплициентой логической функции F (x 1, …, xn), если для любого набора переменных, на котором H (x 1, …, xn) = 0, справедливо и F (x 1, …, xn) = 0. Минимизация логических 4 функций
. МИНИМАЛЬНЫЕ ДИЗЪЮНКТИВНАЯ И КОНЪЮКТИВНАЯ НОРМАЛЬНЫЕ ФОРМЫ (МДНФ И МКНФ) Определение 1: МДНФ булевой функции является дизъюнкция простых импликант. Определение 2: МКНФ булевой функции является конъюнкция простых имплициент. Определение 3: булевая функция G (x 1, …, xn) называется импликантой логической функции F (x 1, …, xn), если для любого набора переменных, на котором G (x 1, …, xn) = 1, справедливо и F (x 1, …, xn) = 1. Определение 4: булевая функция H (x 1, …, xn) называется имплициентой логической функции F (x 1, …, xn), если для любого набора переменных, на котором H (x 1, …, xn) = 0, справедливо и F (x 1, …, xn) = 0. Минимизация логических 4 функций
 МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ ПО КАРТАМ КАРНО Карта Карно – матричная форма представления булевых функций, заданной СДНФ (СКНФ). Выглядит как развертка куба на площади. Аргументы записываются в таком порядке, чтобы соседние отличались не более, чем в одном разряде. Склейке подлежат наборы, для которых единицы (нули) располагаются в соседних клетках матрицы. Причем это должны быть прямоугольные конфигурации единиц (нулей), содержащие число клеток, равное целой степени 2. Получающиеся элементарные конъюнкции (дизъюнкции для СКНФ) определяются как конъюнкция (дизъюнкция) переменных, не меняющих своего значения на всех склеиваемых наборах. Минимизация логических 5 функций
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ ПО КАРТАМ КАРНО Карта Карно – матричная форма представления булевых функций, заданной СДНФ (СКНФ). Выглядит как развертка куба на площади. Аргументы записываются в таком порядке, чтобы соседние отличались не более, чем в одном разряде. Склейке подлежат наборы, для которых единицы (нули) располагаются в соседних клетках матрицы. Причем это должны быть прямоугольные конфигурации единиц (нулей), содержащие число клеток, равное целой степени 2. Получающиеся элементарные конъюнкции (дизъюнкции для СКНФ) определяются как конъюнкция (дизъюнкция) переменных, не меняющих своего значения на всех склеиваемых наборах. Минимизация логических 5 функций
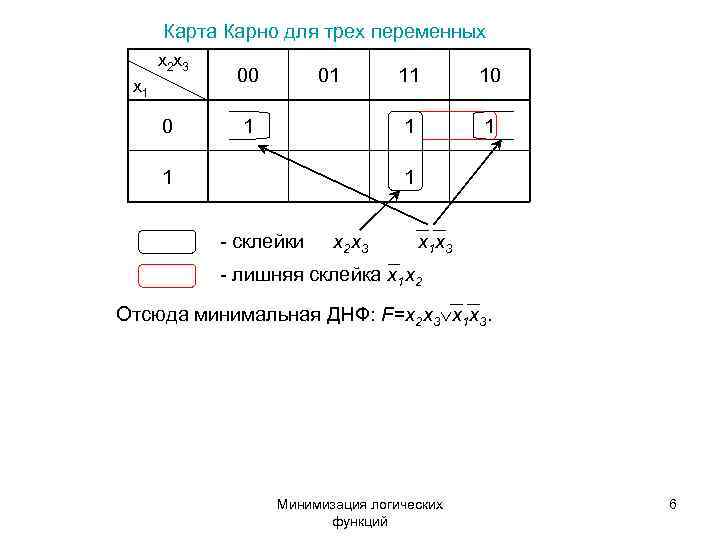
 Карта Карно для трех переменных x 2 x 3 00 01 11 10 x 1 0 1 1 1 - склейки x 2 x 3 x 1 x 3 - лишняя склейка x 1 x 2 Отсюда минимальная ДНФ: F=x 2 x 3 x 1 x 3. Минимизация логических 6 функций
Карта Карно для трех переменных x 2 x 3 00 01 11 10 x 1 0 1 1 1 - склейки x 2 x 3 x 1 x 3 - лишняя склейка x 1 x 2 Отсюда минимальная ДНФ: F=x 2 x 3 x 1 x 3. Минимизация логических 6 функций
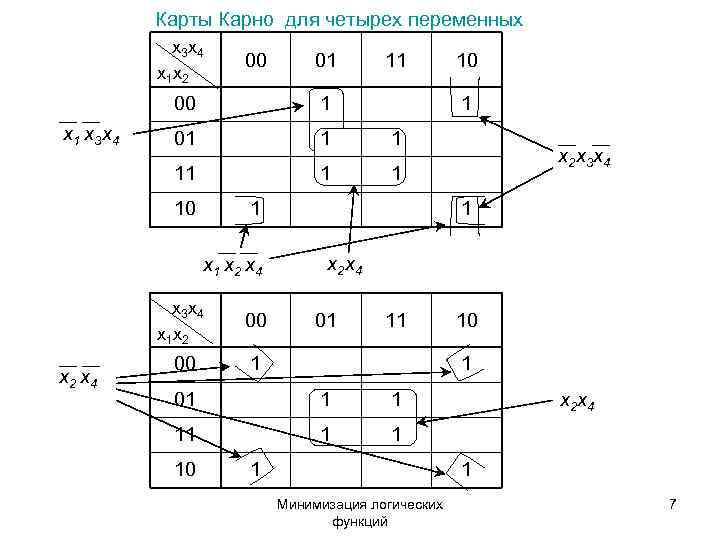
 Карты Карно для четырех переменных x 3 x 4 00 01 11 10 x 1 x 2 00 1 x 1 x 3 x 4 01 х2 x 3 x 4 11 1 10 1 x 1 x 2 x 4 x 2 x 4 x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 x 2 x 4 01 x 2 x 4 11 1 10 1 Минимизация логических 7 функций
Карты Карно для четырех переменных x 3 x 4 00 01 11 10 x 1 x 2 00 1 x 1 x 3 x 4 01 х2 x 3 x 4 11 1 10 1 x 1 x 2 x 4 x 2 x 4 x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 x 2 x 4 01 x 2 x 4 11 1 10 1 Минимизация логических 7 функций
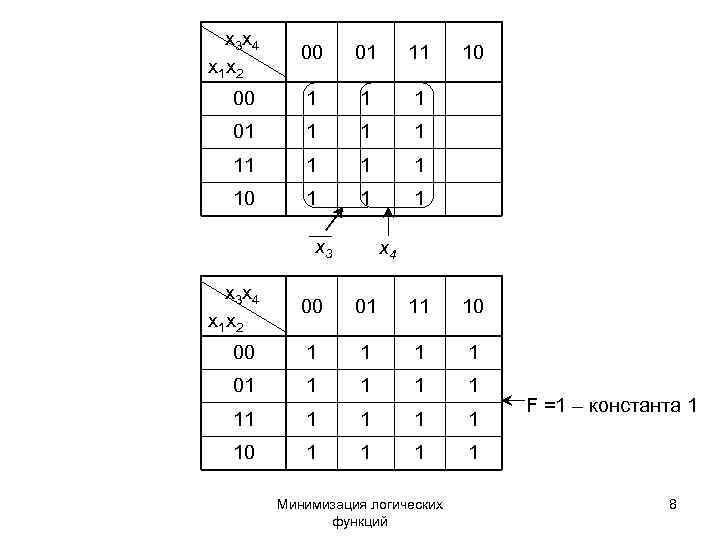
 x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 01 1 10 1 1 x 3 x 4 x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 01 1 1 F =1 – константа 1 1 10 1 1 Минимизация логических 8 функций
x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 01 1 10 1 1 x 3 x 4 x 3 x 4 00 01 11 10 x 1 x 2 00 1 1 01 1 1 F =1 – константа 1 1 10 1 1 Минимизация логических 8 функций
 Карта Карно для пяти переменных Строятся две карты Карно для четырех переменных: одна для х5=0, а вторая для х5=1. По пятой переменной производится склейка в том случае, если при наложении одной карты на другую группы единиц совпадают. x 5=0 x =1 5 x 3 x 4 00 01 11 10 00 01 10 x 1 x 2 00 1 00 1 01 1 01 1 1 1 11 10 1 1 10 х1 х3 х5 х1 х3 х4 Т. е. минимальная ДНФ: F=х1 х3 х5 х1 х3 х4. Минимизация логических 9 функций
Карта Карно для пяти переменных Строятся две карты Карно для четырех переменных: одна для х5=0, а вторая для х5=1. По пятой переменной производится склейка в том случае, если при наложении одной карты на другую группы единиц совпадают. x 5=0 x =1 5 x 3 x 4 00 01 11 10 00 01 10 x 1 x 2 00 1 00 1 01 1 01 1 1 1 11 10 1 1 10 х1 х3 х5 х1 х3 х4 Т. е. минимальная ДНФ: F=х1 х3 х5 х1 х3 х4. Минимизация логических 9 функций
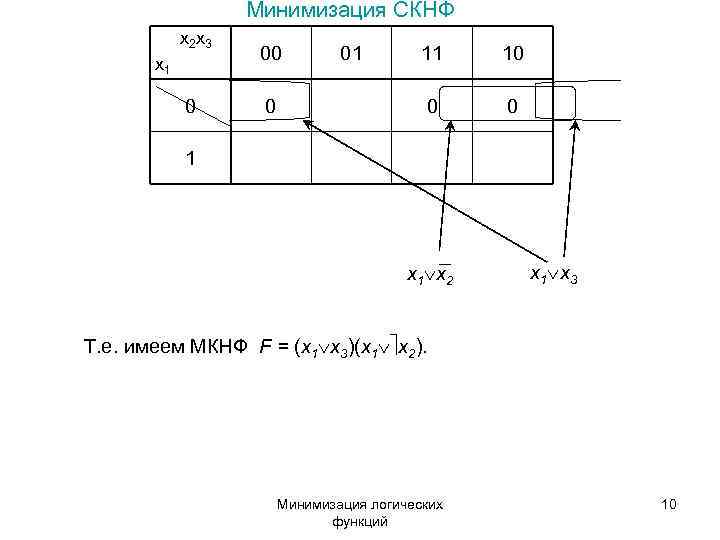
 Минимизация СКНФ x 2 x 3 x 1 00 01 11 10 0 0 0 1 x 1 x 2 x 1 x 3 Т. е. имеем МКНФ F = (x 1 x 3)(x 1 x 2). Минимизация логических 10 функций
Минимизация СКНФ x 2 x 3 x 1 00 01 11 10 0 0 0 1 x 1 x 2 x 1 x 3 Т. е. имеем МКНФ F = (x 1 x 3)(x 1 x 2). Минимизация логических 10 функций
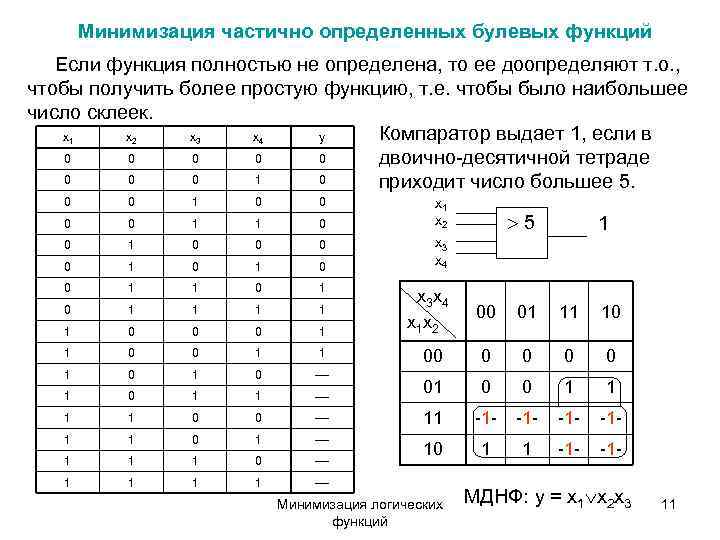
 Минимизация частично определенных булевых функций Если функция полностью не определена, то ее доопределяют т. о. , чтобы получить более простую функцию, т. е. чтобы было наибольшее число склеек. 1 x x 2 x 3 4 x y Компаратор выдает 1, если в 0 0 0 двоично-десятичной тетраде 0 0 0 1 0 приходит число большее 5. 0 0 1 0 0 x 1 0 0 1 1 0 x 2 5 1 0 0 0 x 3 0 1 0 x 4 0 1 1 0 1 x 3 x 4 0 1 1 00 01 10 1 0 0 0 1 x 1 x 2 1 0 0 1 1 00 0 0 1 0 1 0 1 1 01 0 0 1 1 1 1 0 0 11 -1 - 1 1 0 1 10 1 1 -1 - 1 1 1 0 1 1 1 1 Минимизация логических МДНФ: y = x 1 x 2 x 3 11 функций
Минимизация частично определенных булевых функций Если функция полностью не определена, то ее доопределяют т. о. , чтобы получить более простую функцию, т. е. чтобы было наибольшее число склеек. 1 x x 2 x 3 4 x y Компаратор выдает 1, если в 0 0 0 двоично-десятичной тетраде 0 0 0 1 0 приходит число большее 5. 0 0 1 0 0 x 1 0 0 1 1 0 x 2 5 1 0 0 0 x 3 0 1 0 x 4 0 1 1 0 1 x 3 x 4 0 1 1 00 01 10 1 0 0 0 1 x 1 x 2 1 0 0 1 1 00 0 0 1 0 1 0 1 1 01 0 0 1 1 1 1 0 0 11 -1 - 1 1 0 1 10 1 1 -1 - 1 1 1 0 1 1 1 1 Минимизация логических МДНФ: y = x 1 x 2 x 3 11 функций

