Компьютерная графика Фрактальная графика Фрактальная графика является

Компьютерная графика Фрактальная графика

Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики. Фрактальная графика, как и векторная вычисляемая, но отличается тем, что никакие объекты в памяти не хранятся. Изображение строится по уравнению, или системе уравнений, поэтому ничего кроме формулы хранить не надо. Изменив коэффициенты можно получить совершенно другую картину.

Фрактал – структура, состоящая из частей, подобных целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Небольшая часть фрактала содержит информацию о всем фрактале. В простейшем случае часть фрактала представляет собой просто уменьшенный целый фрактал.

Математическая основа - фрактальная геометрия. В основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектовнаследников. Фрактальными свойствами обладают многие объекты живой и неживой природы (снежинка, ветка папоротника)

Снежинка Коха • В центре фрактальной • фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный» . Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3) от стороны исходного фрактального треугольника.

Снежинка Коха • В свою очередь, на средних • Таким образом, отрезках сторон полученных мелкие объекты треугольников, являющихся повторяют свойства объектами-наследниками всего объекта. Процесс первого поколения, наследования можно выстраиваются треугольникипродолжать до наследники второго поколения со стороной (1/9) от стороны бесконечности. исходного треугольника.

Фракталы • Полученный объект носит название фрактальной фигуры. • Изменяя и комбинируя окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию» .

Фрактальная графика • Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник» . Затем идет «Фрактальная фигура» , «Фрактальный объект» ; «Фрактальная прямая» ; «Фрактальная композиция» ; «Объект-родитель» и «Объект наследник» . Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.

КЛАССИФИКАЦИЯ ФРАКТАЛОВ

Геометрические фракталы Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломануюгенератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал. Примером такого фрактального объекта является триадная кривая Коха.

Триадная кривая Коха. Построение кривой начинается с отрезка единичной длины – это нулевое поколение кривой Коха. Далее каждое звено заменяется на образующий элемент, обозначенный на рис. через n=1. Берем отрезок и среднюю его треть переламываем под углом 60 градусов. Затем повторяем эту операцию с каждой из частей получившейся ломаной – и так до бесконечности. В результате мы получим простейший фрактал – триадную кривую.

"Дракон" Хартера-Хейтуэя Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться.

• В компьютерной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. • Двумерные геометрические фракталы используются для создания объемных текстур.

Алгебраические фракталы Это самая крупная группа фракталов. Свое название они получили за то, что их строят на основе алгебраических формул, иногда весьма простых. Методов получения алгебраических фракталов несколько.

Алгебраические фракталы Один из методов представляет собой многократный (итерационный) расчет функции Zn+1= f(Zn), где Z – комплексное число, а f – некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значение функции для разных точек комплексной плоскости может иметь разное поведение: – с течением времени стремится к бесконечности; – стремится к 0; – принимает несколько фиксированных значений и не выходит за их пределы; – поведение хаотично, без каких-либо тенденций.

Множество Мандельброта • Функция : Z[i+1] = Z[i] * Z[i] + C, где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, с центром в точке (0, 0), или после достаточно большого числа итераций (200 -500) Z[i] сойдется к какой-нибудь точке окружности.

Множество Мандельброта • Черный цвет в середине показывает, что в этих точках функция стремится к нулю – это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное это границы множества. Участок границы • Точки принадлежащие границе множества - они то и являются фрактальными - уходят в бесконечность за конечное число итераций, . На границах этого множества функция ведет себя непредсказуемо – хаотично. А точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).

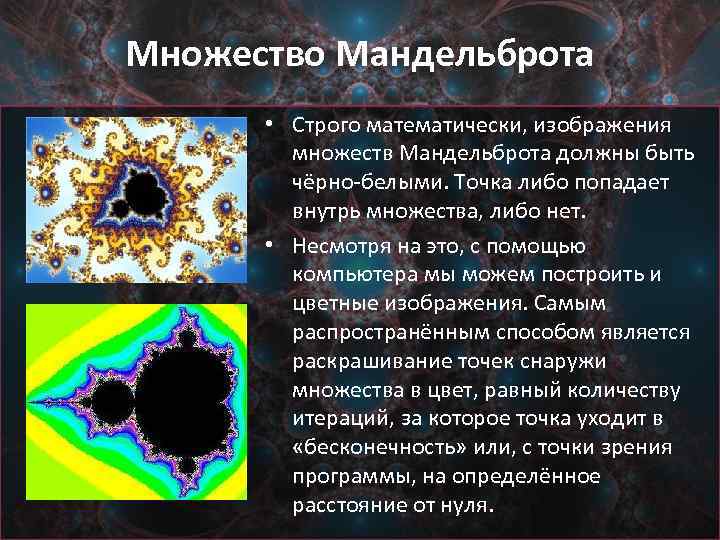Множество Мандельброта • Строго математически, изображения множеств Мандельброта должны быть чёрно-белыми. Точка либо попадает внутрь множества, либо нет. • Несмотря на это, с помощью компьютера мы можем построить и цветные изображения. Самым распространённым способом является раскрашивание точек снаружи множества в цвет, равный количеству итераций, за которое точка уходит в «бесконечность» или, с точки зрения программы, на определённое расстояние от нуля.

Стохастические фракталы • Получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. • Типичный представитель данного класса фракталов «плазма» . • Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число – тем более «рваным» будет рисунок.

Стохастические фракталы • Если, например, сказать, что цвет точки это высота над уровнем моря, то получим вместо плазмы – горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладывается текстура.

Стохастические фракталы • При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т. д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

РЕДАКТОРЫ ФРАКТАЛЬНОЙ ГРАФИКИ

Ultra Fractal http: //www. ultrafractal. com - лучшее решение для создания уникальных фрактальных изображений профессионального качества, которое позволяет не только генерировать фрактальные изображения, но и создавать анимацию на их основе. Созданные изображения можно визуализировать в высоком разрешении, пригодном для полиграфии, и сохранить в собственном формате программы или в одном из популярных фрактальных форматов. • Принцип создания фрактальных изображений достаточно традиционен, самое простое - воспользоваться одной из прилагаемых в поставке формул, а затем отредактировать параметры формулы желаемым образом.

Графический редактор Corel Painter – основанная на принципах фрактальной математики уникальная программа, дающая художнику возможность творить привычными средствами.

Дополнительно 1. Множество Мандельброта