Компьютерная геометрия и графика Лекция 5 Алгоритмы удаления

Компьютерная геометрия и графика Лекция 5 Алгоритмы удаления линий

План лекции 1. 2. Удаление линий и поверхностей 1. Алгоритм плавающего горизонта 2. Алгоритм Робертса 3. Алгоритм z-буфера 4. Построчный алгоритм с z-буфером 5. Алгоритм Варнока 6. Алгоритм трассировки лучей

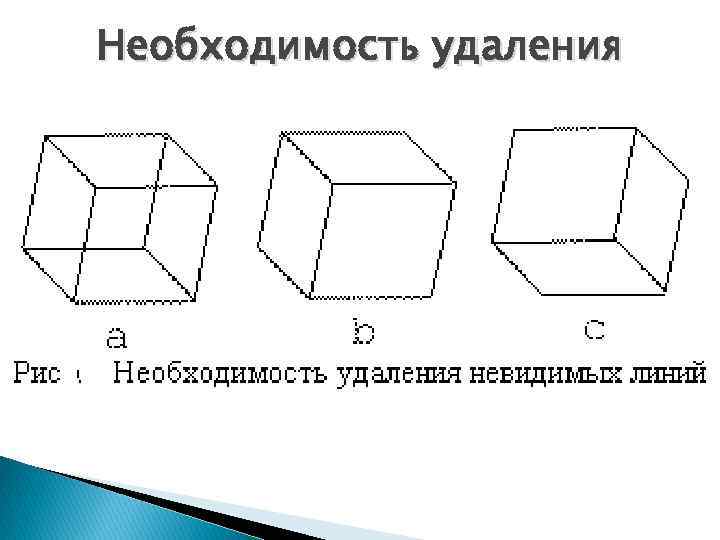Необходимость удаления

Задача удаления Сложность задачи привела к появлению большого числа различных способов ее решения. Наилучшего решения обшей задачи не существует. Для моделирования процессов в реальном времени требуются быстрые алгоритмы. Для машинной мультипликации требуются алгоритмы, которые могут генерировать сложные реалистические изображения. Подобные алгоритмы работают медленно. Учет эффектов прозрачности, фактуры, отражения не входит в задачу удаления. Однако многие из них встроены в алгоритмы удаления и поэтому будут затронуты.

Сортировка ведется по геометрическому расстоянию до точки наблюдения. Основная идея - чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен. После определения расстояний или приоритетов по глубине остается провести сортировку по горизонтали и по вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения. Для повышения эффективности сортировки используется также когерентность сцены, т. е. тенденция неизменяемости характеристик сцены в малом.

Классификация методов удаления 1. По выбору удаляемых частей: удаление невидимых линий, ребер, поверхностей, объемов. 2. По порядку обработки элементов сцены: удаление в произвольном порядке и в порядке, определяемом процессом визуализации. 3. По системе координат: алгоритмы работающие в пространстве объектов, когда каждая из N граней объекта сравнивается с остальными N-1 гранями (объем вычислений растет как N 2), алгоритмы работающие в пространстве изображения, когда для каждого пиксела изображения определяется какая из N граней объекта видна (при разрешении экрана M×M объем вычислений растет как M 2 ×N).

Два подхода к удалению Непосредственное сравнение объектов друг с другом для выяснения того, какие части каких объектов будут являться видимыми. Работа ведется в исходном пространстве объектов. (Алгоритмы в пространстве объекта). Определение для каждого пиксела объекта, какой из них вдоль направления проектирования является ближайшим. При этом работа ведется в пространстве картинной плоскости и существенно используются растровые свойства дисплея. (Алгоритмы в пространстве изображения).

Алгоритм плавающего горизонта чаше всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде: F(x, у, z) = 0. Этот алгоритм обычно работает в пространстве изображения. Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат х, у или z.

Алгоритм плавающего горизонта

Алгоритм плавающего горизонта На рисунке приведен пример, где указанные параллельные плоскости определяются постоянными значениями z. Функция F(x, у, z) = 0 сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например к последовательности у = f(x, z) или х = g (у, z), где z постоянно на каждой из заданных параллельных плоскостей. Поверхность складывается из последовательности кривых, лежащих в каждой из этих плоскостей. Здесь предполагается, что полученные кривые являются однозначными функциями независимых переменных.

Алгоритм плавающего горизонта

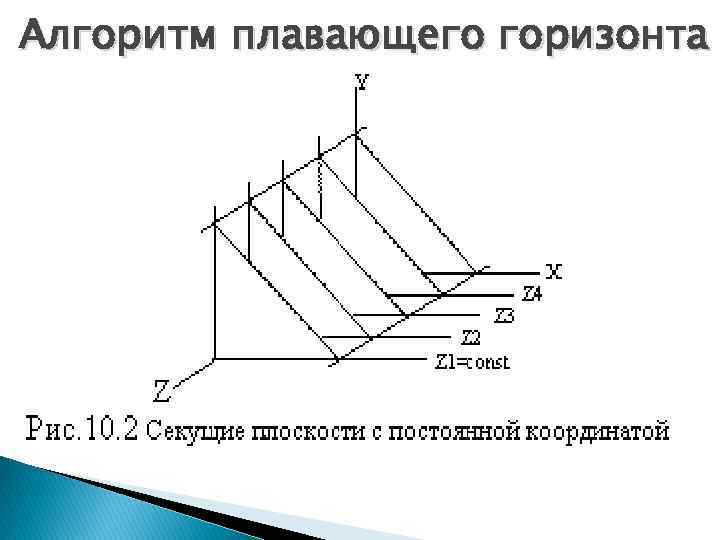
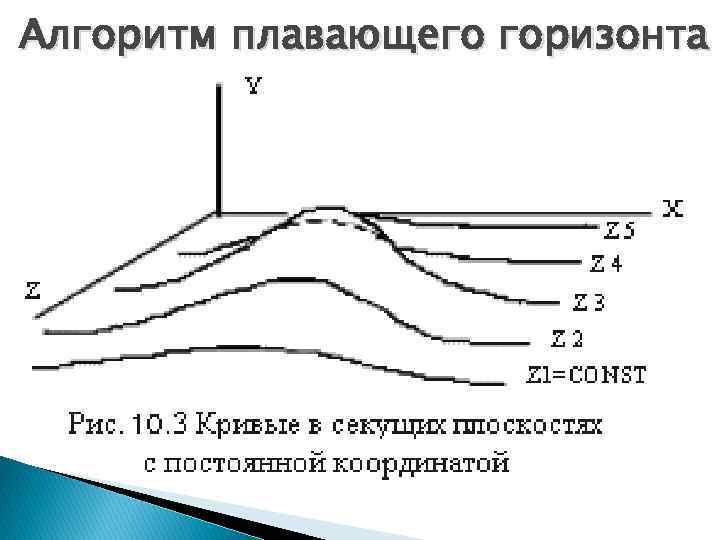
Алгоритм плавающего горизонта 1. Спроецировать полученные кривые на плоскость z=0. 2. Упорядочить плоскости z=const по возрастанию расстояния до них от точки наблюдения. 3. Для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней. 4. Если на текущей плоскости при некотором заданном значении x соответствующее значение у на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.

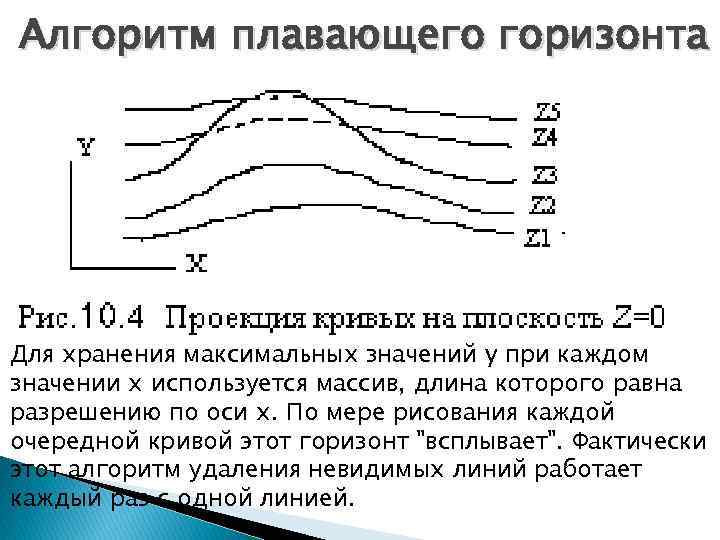Алгоритм плавающего горизонта Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна разрешению по оси x. По мере рисования каждой очередной кривой этот горизонт "всплывает". Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.

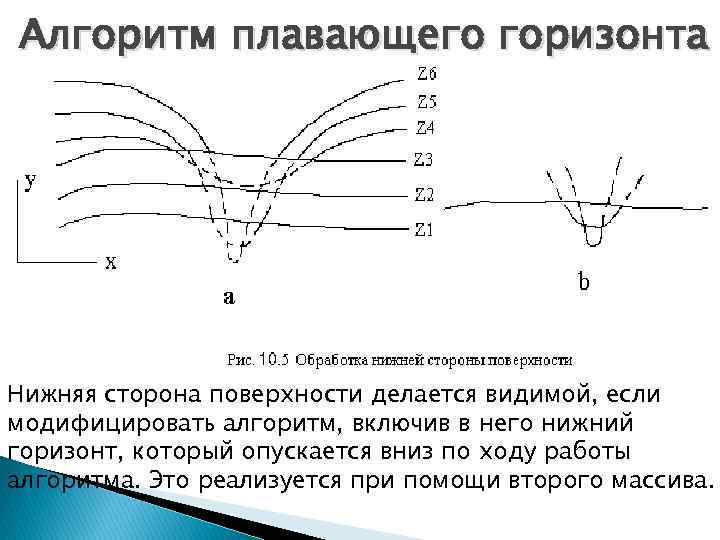Алгоритм плавающего горизонта Нижняя сторона поверхности делается видимой, если модифицировать алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива.

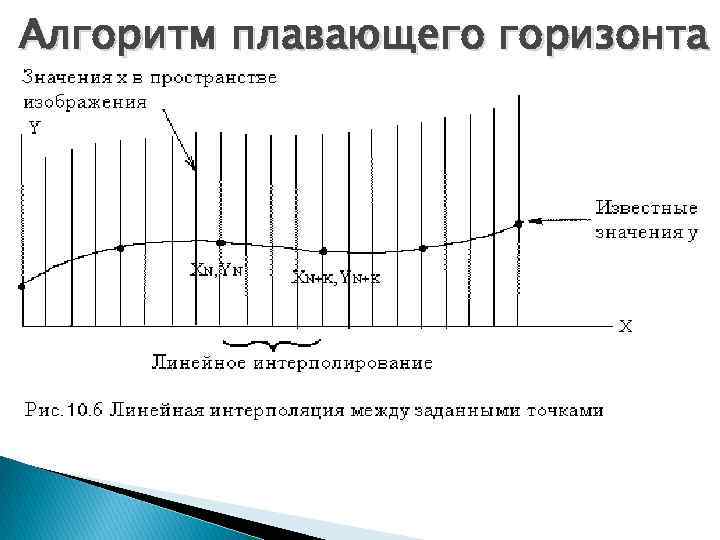Алгоритм плавающего горизонта

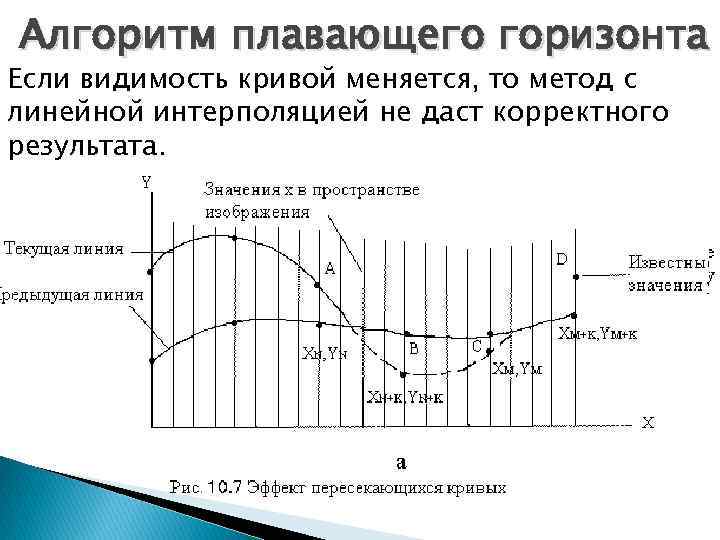Алгоритм плавающего горизонта Если видимость кривой меняется, то метод с линейной интерполяцией не даст корректного результата.

Алгоритм плавающего горизонта

Алгоритм плавающего горизонта При переходе текущей кривой от видимого к невидимому состоянию (сегмент AB), точка (XN+K, YN+K) объявляется невидимой. Тогда участок кривой между точками (XN, YN) и (XN+K, YN+K) не изображается и операция по заполнению массивов не проводится. Образуется зазор между текущей и предыдущей кривыми. Если на участке текущей кривой происходит переход от невидимого состояния к видимому (сегмент CD), то точка (XM+K, YM+K) объявляется видимой, а участок кривой между точками (XM, YM) и (XM+K, YM+K) изображается и операция по заполнению массивов проводится. Поэтому изображается и невидимый кусок сегмента CD.

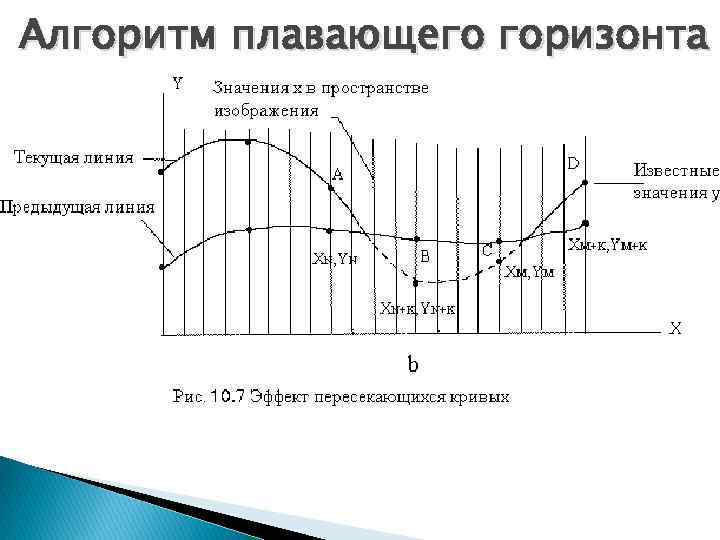
Алгоритм плавающего горизонта Следовательно, необходимо решать задачу о поиске точек пересечения сегментов текущей и предшествующей кривых. Существует несколько методов получения точек пересечения кривых. На растровых дисплеях используется модифицированный алгоритм Брезенхейма, который перед выводом очередного пиксела сравнивает его ординату с верхней и нижними контурными линиями, представляющими в этом случае массивы значений ординат.

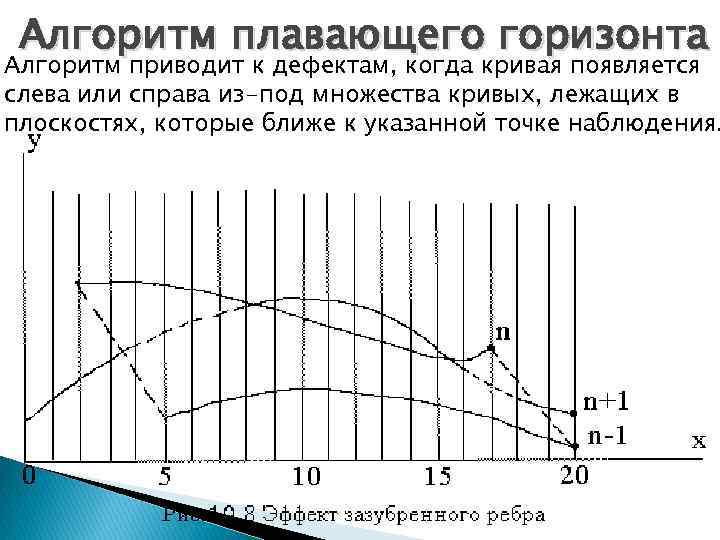Алгоритм плавающего горизонта Алгоритм приводит к дефектам, когда кривая появляется слева или справа из-под множества кривых, лежащих в плоскостях, которые ближе к указанной точке наблюдения.

Алгоритм плавающего горизонта Проблема с зазубренностью боковых ребер решается включением в массивы верхнего и нижнего горизонтов ординат. Обработка левого бокового ребра: Если Рn является первой точкой на первой кривой, то запомним Рn в качестве Рn-1 и закончим заполнение. В противном случае создадим ребро, соединяющее Рn-1 и Рn. Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним Рn в качестве Рn-1. Обработка правого бокового ребра: Если Рn является последней точкой на первой кривой, то запомним Рn в качестве Рn-1 и закончим заполнение. В противном случае создадим ребро, соединяющее Рn и Рn-1. Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним Рn в качестве Рn-1.

Алгоритм Робертса (1969 г. ) Алгоритм Робертса представляет собой первое известное решение задачи об удалении невидимых линий. Алгоритм требует, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые. Алгоритм работает в объектной плоскости. Сначала удаляются из каждого тела те ребра или грани, которые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения какая его часть экранируется этими телами.

Алгоритм Робертса (1969 г. ) Возможны следующие варианты: грань не закрывает ребро; грань полностью закрывает ребро (тогда она удаляется из списка ребер); грань частично закрывает ребро (В этом случае ребро разбивается на несколько частей, из которых видимыми являются не более 2. Само ребро удаляется из списка, но в список добавляются его части не закрываемые гранью).

Алгоритм Робертса (1969 г. ) Можно сократить число проверок, если разбить картинную плоскость на равные клетки. Для каждой клетки составляется список тех граней, проекции которых имеют пересечение с этой клеткой. Для проверки произвольного ребра сначала находятся все клетки, в которые попадает проекция этого ребра, и рассматриваются только те грани, которые содержатся в стеках этих клеток.

Алгоритм Робертса (1969 г. ) Любое выпуклое твердое тело можно выразить матрицей тела Любая точка пространства представима в виде [s]=[x, y, z, 1]. Если точка s лежит на плоскости, то [s][P]T ([P]T - столбец [V]). Если же точка не лежит на плоскости, то знак этого скалярного произведения показывает по какую сторону от плоскости расположена эта точка.

Алгоритм Робертса (1969 г. ) Отрицательность нормали показывает, что она направлена в сторону от наблюдателя и, следовательно, данный многоугольник не виден. Если зритель находится в бесконечности (ось z от наблюдателя), вектор такого наблюдения равен. [E]=[x, y, - µ, 1]. Если скалярное произведение этого вектора на столбец в [V], соответствующий какой-либо плоскости <0, то [E] лежит по отрицательную сторону этой плоскости. Следовательно эти плоскости невидимы из любой точки наблюдения, лежащей в плосости z=-µ. Нулевые результаты соответствуют плоскостям параллельным направлению взгляда.

Алгоритм Робертса (1969 г. ) Этот метод является простейшим алгоритмом удаления невидимых поверхностей для тел, представляющих собой одиночные выпуклые многогранники. Метод используется также для удаления задних граней из сцен перед применением других алгоритмов удаления невидимых линий. Для выпуклых многогранников число граней при этом сокращается наполовину.

Алгоритм Z-буфера Алгоритм предложен Эдом Кэтмулом и представляет собой обобщение буфера кадра. Идея алгоритма состоит в том, чтобы для каждого пиксела дополнительно хранить еще и координату Z или глубину. При занесении очередного пиксела в буфер кадра значение его Z-координаты сравнивается с Z-координатой пиксела, который уже находится в буфере. Если Z-координата нового пиксела больше, чем координата старого, т. е. он ближе к наблюдателю, то атрибуты нового пиксела и его Z-координата заносятся в буфер, если нет, то ни чего не делается.

Алгоритм Z-буфера Этот алгоритм наиболее простой из всех алгоритмов удаления невидимых поверхностей, но требует большого объема памяти. Данные о глубине для реалистичности изображения обычно достаточно иметь с разрядностью порядка 20 бит. Время работы алгоритма не зависит от сложности сцены. Многоугольники, составляющие сцену, могут обрабатываться в произвольном порядке. Для сокращения затрат времени нелицевые многоугольники могут быть удалены.

Алгоритм Z-буфера Общая схема алгоритма: Инициализировать кадровый и Z-буфера. Кадровый буфер закрашивается фоном. Z-буфер закрашивается минимальным значением Z. Выполнить преобразование каждого многоугольника сцены в растровую форму. При этом для каждого пиксела вычисляется его глубина z. Если вычисленная глубина больше, чем глубина, уже имеющаяся в Z-буфере, то занести в буфера атрибуты пиксела и его глубину, иначе никаких занесений не выполнять. Выполнить, если это было предусмотрено, усреднение изображения с понижением разрешения.

Построчный алгоритм Z-буфера Изображение можно представить как ряд линий. Рассмотрим сечение плоскостью, проходящей через линию и центр проектирования. Для каждой сканирующей строки буфер кадра инициализируется фоновым значением интенсивности, а z-буфер минимальным значением z координаты. Определяется пересечение сканирующей строки с двумерной проекцией каждого многоугольника сцены. Глубина каждого элемента плоскости вдоль отрезка, образующегося при пересечении, сравнивается с глубиной в соответствующем элементе z-буфера.

Алгоритм Варнока Алгоритм работает в пространстве изображения и анализирует область на экране дисплея на наличие в них видимых элементов. Если в окне нет изображения, то оно просто закрашивается фоном. Если же в окне имеется элемент, то проверяется достаточно ли он прост для визуализации. Если объект сложный, то окно разбивается на более мелкие, для каждого из которых выполняется тест на отсутствие и/или простоту изображения. Рекурсивный процесс разбиения может продолжаться до тех пор пока не будет достигнут предел разрешения экрана.

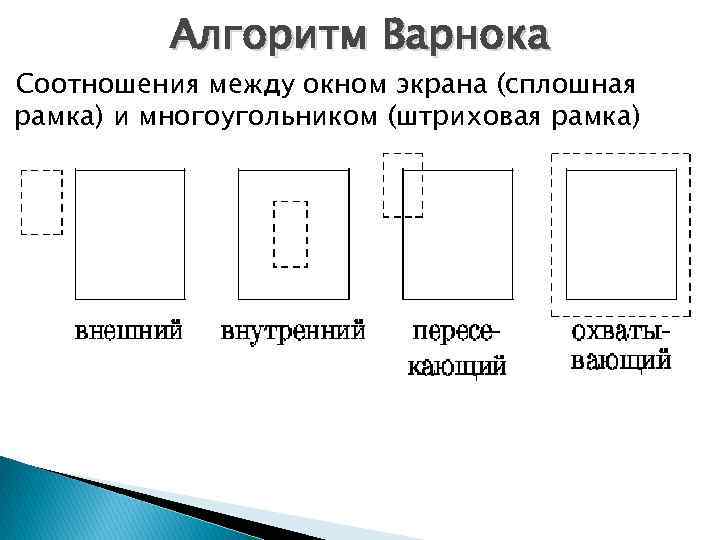Алгоритм Варнока Соотношения между окном экрана (сплошная рамка) и многоугольником (штриховая рамка)

Алгоритм Варнока В 4 случаях можно сразу принять решение: все многоугольники сцены - внешние по отношению к окну. Окно закрашивается фоном; Имеется один внутренний или пересекающий многоугольник. Все окно закрашивается фоном и затем часть окна, соответствующая внутреннему или пересекающему окну закрашивается цветом многоугольника; имеется единственный охватывающий многоугольник. Окно закрашивается его цветом. имеется несколько многоугольников и хотя бы один из них охватывающий. Если охватывающий многоугольник расположен ближе остальных, то окно закрашивается его цветом.

Алгоритм Варнока В любых других случаях процесс разбиения окна продолжается. Если достигнуто максимальное разбиение, но не обнаружено ни одного из приведенных четырех случаев, то для точки с центром в полученном минимальном окне (размером в пиксель) вычисляются глубины оставшихся многоугольников и закраску определяет многоугольник, наиболее близкий к наблюдателю. При этом для устранения лестничного эффекта можно выполнить дополнительные разбиения и закрасить пиксел с учетом всех многоугольников, видимых в минимальном окне.

Алгоритм Варнока Первые три случая идентифицируются легко. Последний же случай сводится к поиску охватывающего многоугольника, перекрывающего все остальные многоугольники, связанные с окном. Проверка на такой многоугольник может быть выполнена следующим образом: в угловых точках окна вычисляются Z-координаты для всех многоугольников, связанных с окном. Если все четыре такие Z-координаты охватывающего многоугольника ближе к наблюдателю, чем все остальные, то окно закрашивается цветом соответствующего охватывающего многоугольника. Если же нет, то мы имеем сложный случай и разбиение следует продолжить.

Алгоритм Варнока После разбиения окна охватывающие и внешние многоугольники наследуются от исходного окна. Поэтому необходимо проверять лишь внутренние и пересекающие многоугольники. Важной частью алгоритма является определение расположения многоугольника относительно окна.

Алгоритм трассировки лучей Удаление невидимых (скрытых) поверхностей в алгоритме трассировки лучей выполняется следующим образом: сцена преобразуется в пр-во изображения, из точки наблюдения в каждый пиксель экрана проводится луч и определяется какие именно объекты сцены пересекаются с лучом, вычисляются и упорядочиваются по Z координаты точек пересечения объектов с лучом. В простейшем случае для непрозрачных поверхностей без отражений и преломлений видимой точкой будет точка с максимальным значением Z-координаты. Для более сложных случаев требуется сортировка точек пересечения.

Алгоритм трассировки лучей Наиболее важная часть алгоритма - процедура определения пересечения, которая в принципе выполняется Rx×Ry×N раз (здесь Rx, Ry разрешение дисплея по X и Y, соответственно, а N - количество многоугольников в сцене). Повышение эффективности может достигаться сокращением времени вычисления пересечений и избавлением от ненужных вычислений. Последнее обеспечивается использованием геометрически простой оболочки, объемлющей объект. Используют прямоугольную оболочку и сферическую.

Алгоритм трассировки лучей Дальнейшее сокращение расчетов пересечений основывается на использовании групп пространственно связанных объектов. Для сокращения расчетов пересечений используется отложенное вычисление пересечений с объектами. Дополнительное сокращение объема вычислений может достигаться отбрасыванием нелицевых граней, учетов связности строк растрового разложения и т. д.