Компьютерная геометрия и графика Лекция 3 Базовая графика

Компьютерная геометрия и графика Лекция 3 Базовая графика. Математические основы.

План лекции 1. Представление и преобразование точек в пространстве. Однородные координаты. a. b. c. d. e. f. 2. 3. 4. Трехмерное вращение. Трехмерное изменение масштаба. Трехмерный перенос. Трехмерный сдвиг. Отображение в пространстве. Трехмерное вращение вокруг произвольной оси. Аффинная и перспективная геометрия. Трехмерные проекции. a. Центральные проекции. b. Параллельные проекции. c. Математическое описание. Графика в Pascal

Представление и преобразование точек. Однородные координаты. Для наилучшего восприятия формы объекта необходимо иметь его изображение в трехмерном пространстве. Наглядное представление об объекте можно получить путем выполнения операций вращения и переноса, а также построения проекций. Точка в трехмерном пространстве - [ x y z]. Та же точка в однородных координатах - [x y z 1].

Однородные координаты. Матричное представление преобразований. Преобразование в однородных координатах описывается соотношениями:

Однородные координаты. Матричное представление преобразований. Матрица 3 x 3 осуществляет линейное преобразование в виде изменения масштаба, сдвига и вращения. Матрица-строка 1 х3 производит перенос.

Однородные координаты. Матричное представление преобразований. Полное преобразование, полученное путем воздействия на вектор положения матрицей 4 Х 4 и нормализации преобразованного вектора, будем называть билинейным преобразованием. Оно обеспечивает выполнение комплекса операций сдвига, частичного изменения масштаба, вращения, отображения, переноса, а также изменения масштаба изображения в целом.

Однородные координаты. Матричное представление преобразований. Трехмерное вращение вдоль оси х. Вращение предполагается положительным, т. е. по часовой стрелке, если смотреть из начала координат вдоль оси вращения.

Однородные координаты. Матричное представление преобразований. Трехмерное вращение вдоль оси y. Вращение предполагается положительным, т. е. по часовой стрелке, если смотреть из начала координат вдоль оси вращения.

Однородные координаты. Матричное представление преобразований. Трехмерное вращение вдоль оси z. Вращение предполагается положительным, т. е. по часовой стрелке, если смотреть из начала координат вдоль оси вращения.

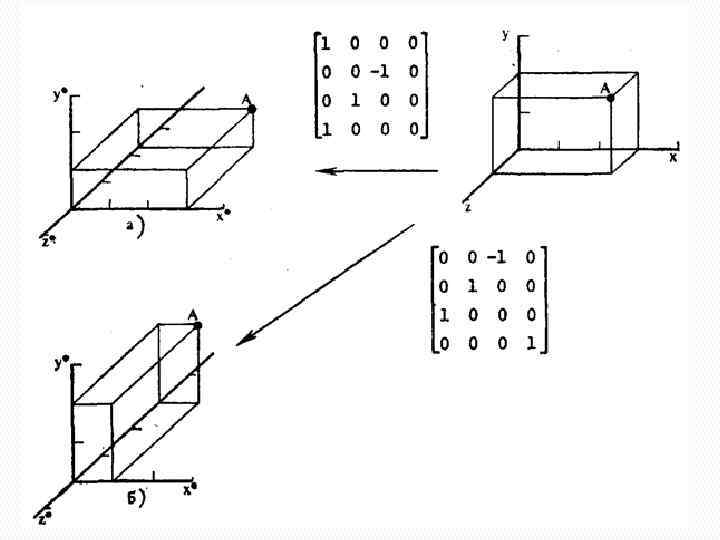
Однородные координаты. Матричное представление преобразований. Так как вращения описываются умножением матриц, то трехмерные вращения некоммутативны, т. е. порядок умножения будет влиять на конечный результат. Для того чтобы показать это, рассмотрим вращение вокруг оси х, за которым следует вращение на такой же угол вокруг оси у и наоборот.

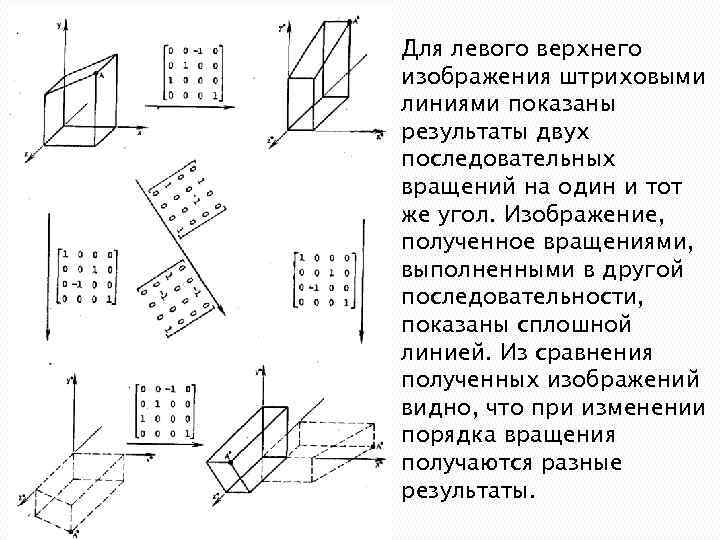
Для левого верхнего изображения штриховыми линиями показаны результаты двух последовательных вращений на один и тот же угол. Изображение, полученное вращениями, выполненными в другой последовательности, показаны сплошной линией. Из сравнения полученных изображений видно, что при изменении порядка вращения получаются разные результаты.

Однородные координаты. Матричное представление преобразований. Трехмерное изменение масштаба.

Однородные координаты. Матричное представление преобразований. Трехмерный перенос.

Однородные координаты. Матричное представление преобразований. Трехмерный сдвиг.

Однородные координаты. Матричное представление преобразований. Трехмерное отображение относительно плоскости xy.

Однородные координаты. Матричное представление преобразований. Трехмерное отображение относительно плоскости xz.

Однородные координаты. Матричное представление преобразований. Трехмерное отображение относительно плоскости yz.

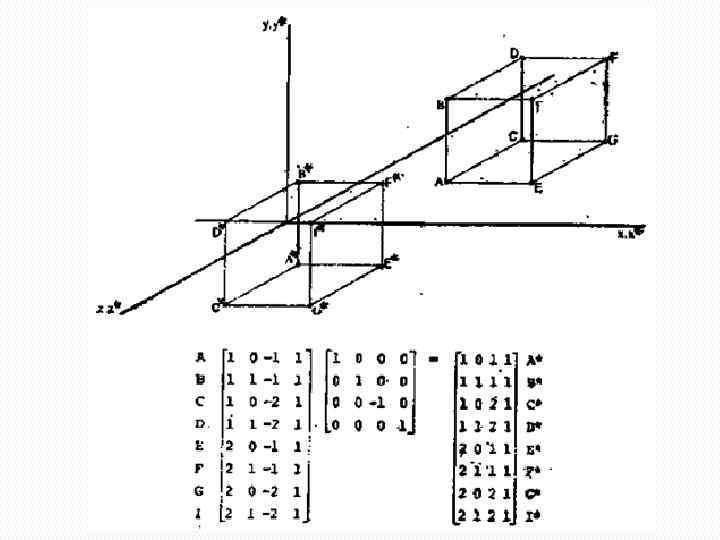
Однородные координаты. Матричное представление преобразований. Вращения около произвольной оси в трехмерном пространстве задается композицией трехмерных преобразований: Перенос изображения и заданной оси вращения в начало координат; Поворот относительно оси; Перенос в первоначальное положение.

Аффинная и перспективная геометрия. Идея описания точки вектором возникла из геометрических представлений. Здесь важными являются понятие параллельности и соотношения между параллельными линиями. Аффинное преобразование является комбинацией линейных преобразований, сопровождаемых переносом изображений. Для аффинного преобразования последний столбец в обобщенной матрице преобразования размера 4 х4 должен быть равен [0 0 0 1] Аффинные преобразования формируют удобную подсистему билинейных преобразований, так как произведение двух аффинных преобразований также является аффинным. Это позволяет представить обобщенную ориентацию системы точек по отношению к произвольной координатной системе.

Аффинная и перспективная геометрия. Перспективными изображениями часто пользуются художники и архитекторы, так как эти изображения позволяют получить картину, близкую к реальной, однако из-за сложности построений их редко используют конструкторы. В тех случаях, когда для машинного представления изображения используются однородные координаты, одинаково легко могут быть получены как аффинные, так и перспективные преобразования. В перспективной геометрии нет двух линий, параллельных другу, и перспективная плоскость может быть рассмотрена как полусферическая поверхность, а перспективное преобразование - как преобразование из одного трехмерного пространства в другое.

Аффинная и перспективная геометрия. Перспективное преобразование имеет место в случае, когда последний столбец обобщенной матрицы преобразования 4 х4 не нулевой. Часто перспективное преобразование ассоциируется с построением проекции на плоскости, например, из точки z = c 1, именуемой центром проекции. Комбинация перспективного преобразования с проекционным образует перспективную проекцию. Перспективная проекция представляет собой преобразование изображения из трехмерного пространства в двумерное.

Аффинная и перспективная геометрия. Если центр проецирования располагается в бесконечности, то перспективная проекция называется аксонометрической. Иными словами, вид проекции зависит от расположения этого центра. Аксонометрическая проекция получается с помощью аффинного преобразования, определитель которого равен нулю. Существуют несколько типов аксонометрических проекций, которые находят применение в начертательной геометрии и инженерной графике. Для получения математических зависимостей, описывающих аксонометрические проекции, используется матрица преобразования размера 4 х4, необходимая для проведения аффинного преобразования системы точек. Точки затем проецируются на плоскость из центра проецирования в бесконечности.

Аффинная и перспективная геометрия. Классификация общих аксонометрических проекций Ортогональная. Диметрическая. Изометрическая. Матрица преобразования осуществляет только вращение; таким образом, координатные оси остаются ортогональными во время проецирования. Две из трех осей во время проецирования одинаково сокращены. Все три оси во время проецирования одинаково сокращены.

Трехмерные проекции. В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в точки системы координат размерностью, меньшей, чем n. В рассматриваемом случае с помощью проецирования три измерения отображаются в два. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проецирующих лучей, которые называются проекторами и которые выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

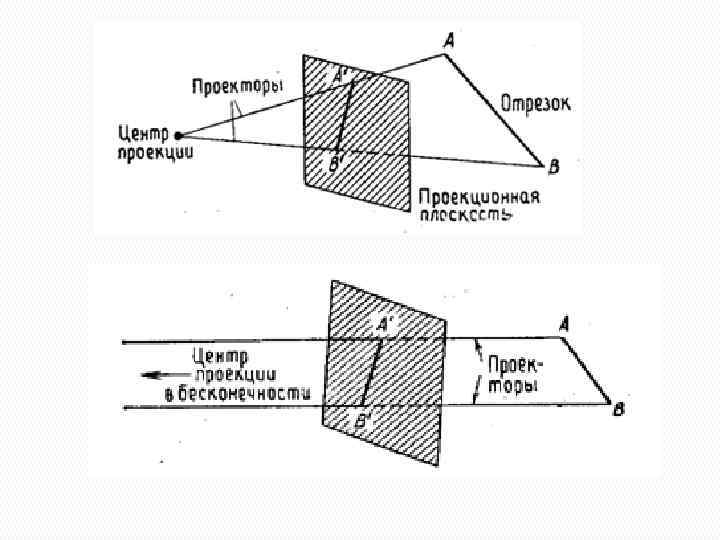
Трехмерные проекции. Определенный таким образом класс проекций известен под названием плоских геометрических проекций. Плоские геометрические проекции, которые в дальнейшем будем называть просто проекциями, можно подразделить на два основных класса: центральные и параллельные. Различие между ними определяется соотношением между центром проекции и проекционной плоскостью. Если расстояние между ними конечно, то проекция будет центральной, если же оно бесконечно, то проекция будет параллельной. Параллельные проекции названы так потому, что центр проекции бесконечно удален и все проекторы параллельны. При описании центральной проекции мы явно задаем ее центр проекции, в то время как определяя параллельную проекцию, мы указываем направление проецирования.

Трехмерные проекции. Центральная проекция порождает визуальный эффект, аналогичный тому, к которому приводят фотографические системы или зрительная система человека, и поэтому используется в случаях, когда желательно достичь определенной степени реальности. Этот эффект известен как перспективное укорачивание: размер центральной проекции объекта изменяется обратно пропорционально расстоянию от центра проекции до объекта. Это означает, что, хотя центральная проекция объектов является реалистичной, она оказывается непригодной для представления точной формы и размеров объектов: из проекции нельзя получить информацию о расстояниях; углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости; проекции параллельных линий в общем случае не параллельны.

Трехмерные проекции. Параллельная проекция порождает менее реалистичное изображение, поскольку отсутствует перспективное укорачивание, хотя при этом могут иметь место различные постоянные укорачивания вдоль каждой из осей. Проекция фиксирует истинные размеры (с точностью до скалярного множителя), и параллельные прямые остаются параллельными. Как и в случае центральной проекции, углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости. Чертежнику легче изображать параллельные проекции, чем центральные, однако что проще в случае машинной графики - неясно.

Трехмерные проекции. Центральные проекции любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будут сходиться в точке схода. Параллельные прямые в трехмерном пространстве пересекаются лишь в бесконечности, поэтому точку схода можно представить себе как проекцию точки, находящейся в бесконечности. Существует, разумеется, бесконечное число точек схода.

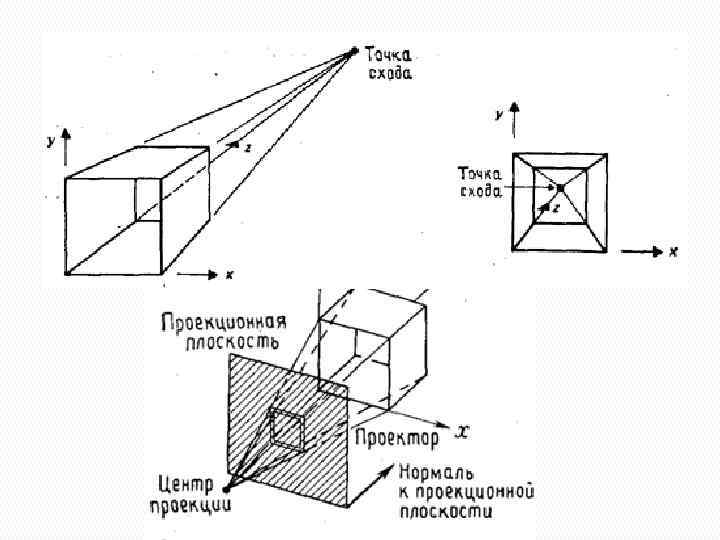
Трехмерные проекции. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Например, если проекционная плоскость пересекает одну только ось z (и, следовательно, перпендикулярна ей), то лишь на этой оси будет лежать главная точка схода, поскольку прямые, параллельные как оси у, так и оси x, параллельны также и проекционной плоскости и поэтому не имеют точки схода.

Трехмерные проекции. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно, и от числа координатных осей, которые пересекает проекционная, плоскость. Двухточечная центральная проекция широко применяется в архитектурном, инженерном и промышленном проектировании и в рекламных изображениях, в которых вертикальные прямые проецируются как параллельные и, следовательно, не сходятся. Трехточечные центральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.

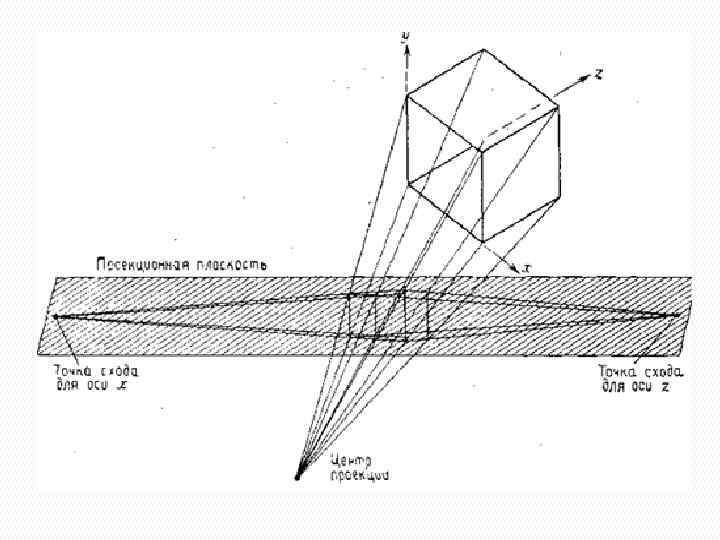
Трехмерные проекции. Параллельные проекции разделяются на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости. В ортографических параллельных проекциях эти направления совпадают, а в косоугольных параллельных проекциях они не совпадают. То есть в ортографических проекциях направление проецирования является нормалью к проекционной плоскости.

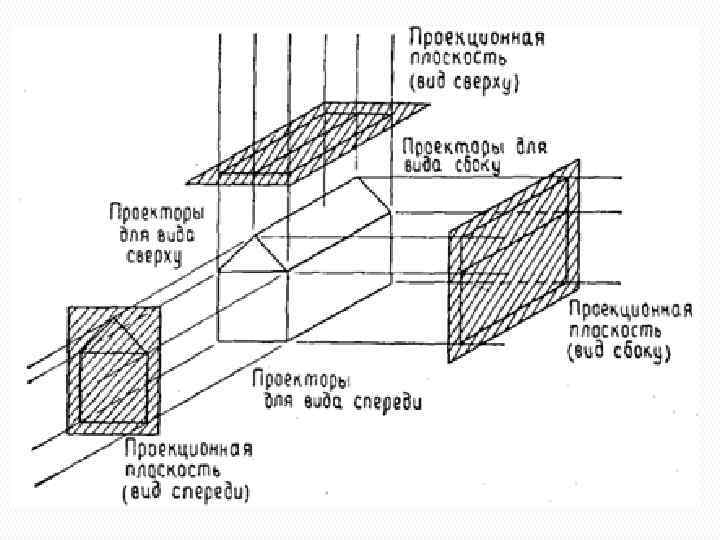
Трехмерные проекции. Наиболее широко используемыми видами ортографических проекций являются вид спереди, вид сверху (план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проецирования. Эти три проекции часто применяются в инженерной графике для описания машиностроительных деталей, агрегатов и сооружений, так как по ним можно измерять расстояния и углы. Поскольку каждая проекция отображает лишь одну сторону объекта, часто совсем непросто представить себе пространственную структуру проецируемого объекта, даже если рассматривать сразу несколько проекций одного и того же объекта.

Трехмерные проекции. В случае аксонометрических ортографических проекций используются проекционные плоскости, не перпендикулярные главным координатным осям, поэтому на них изображаются сразу несколько сторон объекта, так же как и при центральном проецировании, однако в аксонометрии укорачивание постоянно, тогда как в случае центральной проекции оно связано с расстоянием от центра проекции. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояния же можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).

Трехмерные проекции. Широко используемым видом аксонометрической проекции является изометрическая проекция. В этом случае нормаль к проекционной плоскости составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (а, b, с), то потребуем, чтобы |a|=|b|=|c|). Существуют лишь четыре различные изометрические проекции. Единичными нормалями этих направлений являются векторы (а, а, а), (-а, а, а), (а, -а, а) и (а, а, -а). Изометрическая проекция обладает следующим свойством: все три главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом (изо - "равно» , метрия - "измерение"). Главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом.

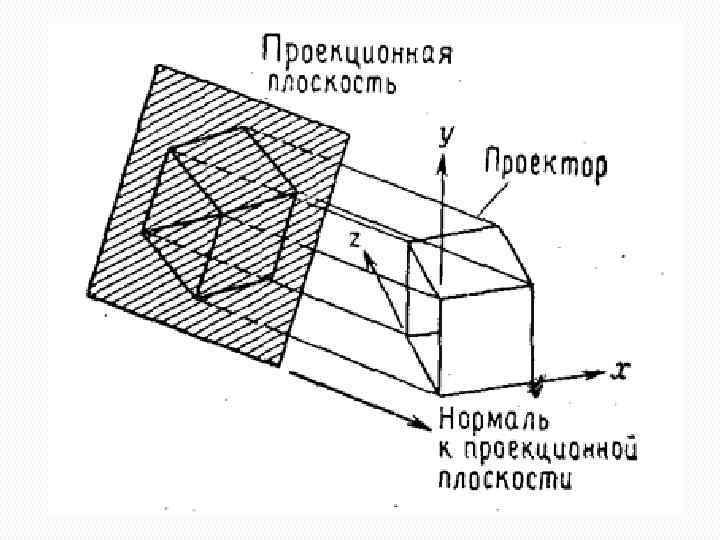
Трехмерные проекции. Косоугольные проекции сочетают в себе свойства ортографических проекций со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерять углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Благодаря этим свойствам, а также простоте построения косоугольные проекции широко (хотя и не слишком) используются. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают.

Трехмерные проекции. Двумя важными видами косоугольных проекций являются проекции Кавалье (cavalier) (горизонтальная косоугольная изометрия) и Кабине (cabinet)(фронтальная косоугольная диметрия). В проекции Кавалье направление проецирования составляет с плоскостью угол 45°. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т. е. укорачивание отсутствует. Проекция Кабине имеет направление проецирования, которое составляет с проекционной плоскостью угол arctg(1/2). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют 1/2 их действительной длины. Проекции кабине являются более реалистичными, чем проекции Кавалье, поскольку укорачивание с коэффициентом 1/2 больше согласуется с нашим визуальным опытом.

Трехмерные проекции. Для простоты будем считать, что при центральном проецировании картинная плоскость перпендикулярна оси z и совпадает с плоскостью z=d, а при параллельном совпадает с плоскостью z=0. Проекции рассматриваются в системе координат наблюдателя, которая является левосторонней. Система координат, в которой ось х направлена вправо, ось у - вверх, а ось z - внутрь экрана, естественно согласуется с экраном дисплея.

Трехмерные проекции. Каждую из проекций можно описать матрицей размером 4 х4. Этот способ оказывается удобным, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования, представив в результате две операции (преобразование и проецирование) в виде одной матрицы.

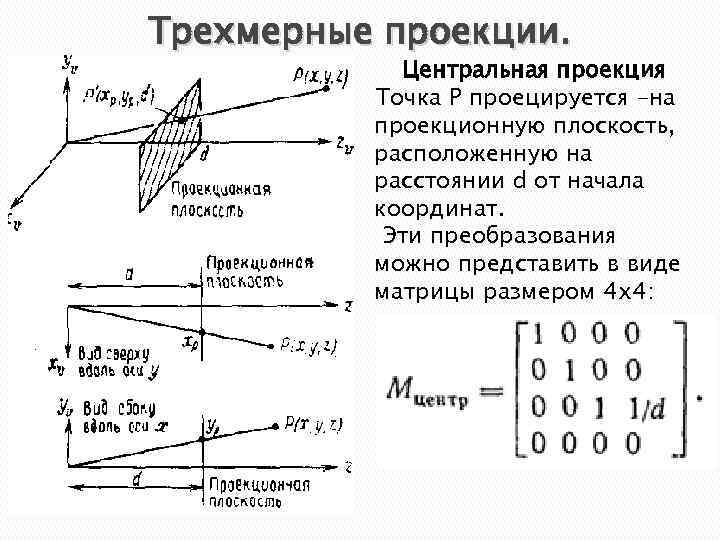
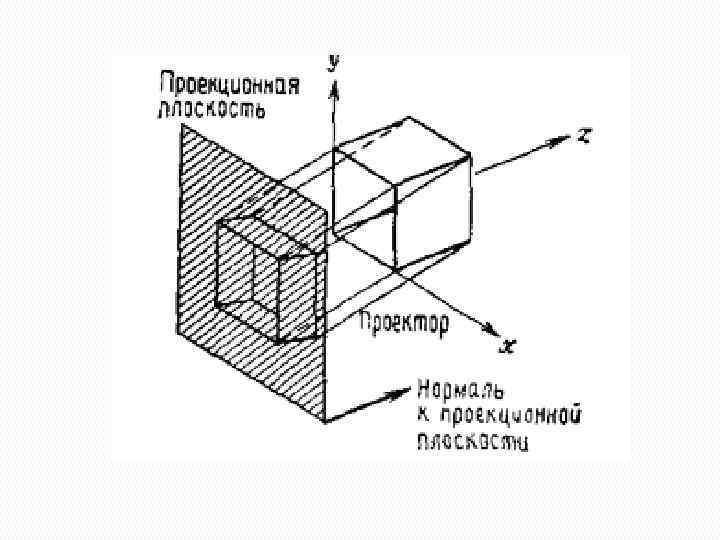
Трехмерные проекции. Центральная проекция Точка P проецируется -на проекционную плоскость, расположенную на расстоянии d от начала координат. Эти преобразования можно представить в виде матрицы размером 4 х4:

Трехмерные проекции. Ортографическое проецирование на плоскость z=0. Направление проецирования совпадает с нормалью к плоскости проекции, т. е. в нашем случае с осью z. Эта проекция описывается матрицей

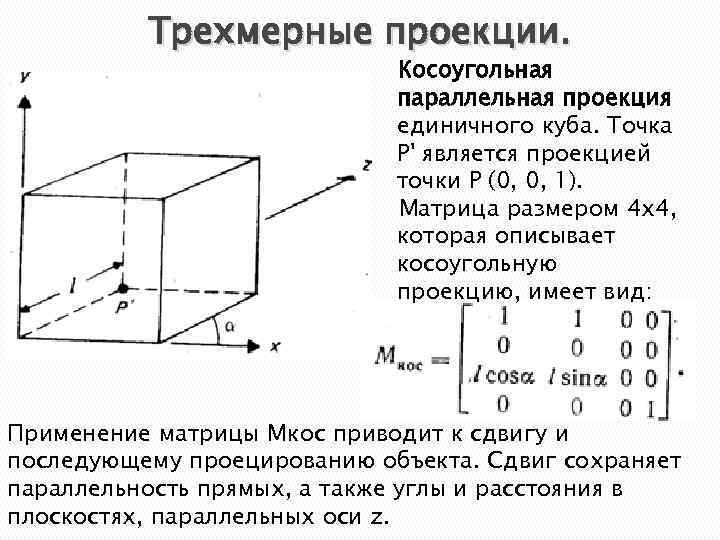
Трехмерные проекции. Косоугольная параллельная проекция единичного куба. Точка Р' является проекцией точки P (0, 0, 1). Матрица размером 4 х4, которая описывает косоугольную проекцию, имеет вид: Применение матрицы Mкос приводит к сдвигу и последующему проецированию объекта. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных оси z.

Графика в Pascal. Множество графических процедур и функций среды программирования Pascal собраны в модуле Graph. Для подключения библиотеки графических функций и процедур необходимо подключить модуль к вашей программе строкой Uses graph ; Взаимодействие программы и видеосистемы в графических режимах обеспечивают драйверы. Драйверы собраны в файлах, имеющих расширение BGI: CGA. BGI , EGAVGA. BGI , HERC. BGI , IBM 8514. BGI , ATT. BGI , PC 3270. BGI и др.

Графика в Pascal. Для инициализации графического режима используется процедура: Init. Graph(var Driver, Mode: integer; Path: string); где Driver – переменная типа integer , определяющая тип графического драйвера; Mode – переменная того же типа, задающая режим работы графического адаптера; Path – выражение типа string , содержащее путь доступа к файлу драйвера.

Графика в Pascal. Пример фрагмента программы, где инициализируется графический режим Program primer ; Uses graph ; Var D , m : integer ; {переменные для установки драйвера и режима работы} Begin D : =9; M : =2; Init. Graph ( d , m , ‘здесь нужно указать путь к драйверу EGAVGA. BGI ’} ……

Графика в Pascal. Наиболее простой способ выбора графического драйвера и режима – автоматический ( detect ). Пример фрагмента программы, где инициализируется графический режим Program primer ; Uses graph ; Var D , m : integer ; {переменные для установки драйвера и режима работы} Begin D : = detect ; Init. Graph ( d , m , ‘здесь нужно указать путь к драйверу EGAVGA. BGI ’}

Графика в Pascal. Проверка результата инициализации графического режима. Для проверки успешности инициализации графического режима существует функция Graph. Result, которая имеет тип результата integer , в котором закодирован результат последнего обращения к графическим процедурам. Если ошибка не обнаружена, значением функции будет 0, в противном случае – отрицательное число. Завершение работы графического режима. Завершает работу адаптера в графическом режиме и восстанавливает текстовый режим работы экрана процедура Close. Graph.

Графика в Pascal. Пример заготовки к графическому режиму Program primer ; Uses graph ; Var D , m : integer : {переменные для установки драйвера, режима} Begin D: = detect; Inir. Graph(d, m, ‘ путь к драйверу ’); If Grapf. Result =0 then {если инициализация прошла успешно} begin <описание всех построений> close. Graph ; end else writeln (‘произошла ошибка при инициализации графики’); end.