Комплексные числа Лекция № 2 Определение комплексного

Комплексные числа Лекция № 2

Определение комплексного числа При рассмотрении ряда задач действительных чисел «не хватает» . Например, уравнение x 2 + 1 = 0 не имеет решения на множестве действительных чисел. Возникает потребность в расширении понятия числа. Действительные числа «заполняют» всю числовую ось. Поэтому остаётся возможность отождествить новые числа с точками плоскости. Опр. 1. Введем на плоскости прямоугольную систему координат XOY. Каждая точка плоскости однозначно определяется своими координатами (x; y). Назовем комплексным числом z пару действительных чисел (x; y) (порядок важен) со следующими операциями: 1. Сложение. Если z 1 = (x 1; y 1), z 2 = (x 2; y 2), то 2. Умножение: 2

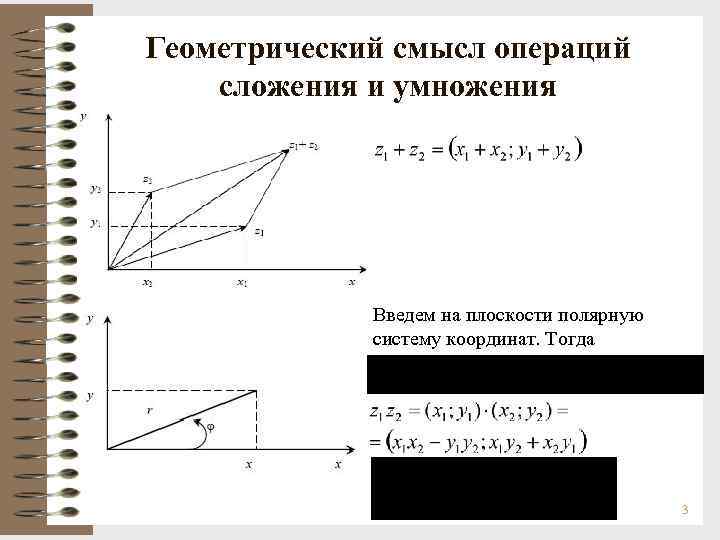Геометрический смысл операций сложения и умножения Введем на плоскости полярную систему координат. Тогда 3

Рассмотрим комплексные числа вида z = (x; 0). Они располагаются на оси OX. Для таких чисел операции сложения и умножения превращаются в обычные операции сложения и умножения действительных чисел. Каждое действительное число x отождествляем с комплексным числом вида z = (x; 0). Рассмотрим специальное число i = (0; 1). Тогда Число i – мнимая единица. Каждое мнимое число выражаем через i: z = (0; y) = iy Стандартная запись комплексного числа: x = Rez – действительная, y = Imz – мнимая части комплексного числа z. 4

Операции сложения и умножения комплексных чисел, записанных в стандартной форме: Модулем комплексного числа z = x + iy называется Свойства операций сложения и умножения: 1. Коммутативность. z 1 + z 2 = z 2 + z 1. 2. Ассоциативность. (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3). 3. Дистрибутивность. (z 1 + z 2)z 3 = z 1 z 3 + z 2 z 3. Вычитание комплексных чисел: 5

Деление комплексных чисел: Пример 1. Выполнить арифметические действия над комплексными числами z 1 = 1 + i, z 2 = 1 – i. Пример 2. Найти модуль числа z = 3 – 4 i. 6

Тригонометрическая форма комплексного числа Арифметические операции над комплексными числами в тригонометрической форме. 1. Умножение: 2. Деление: 3. Формулы Муавра: 7

Извлечение корня n-й степени из комплексного числа Рассмотрим вопрос об извлечении корня n-ой степени из числа z = r(cos + i sin ). Это означает, что требуется найти такое комплексное число w = (cos + i sin ), чтобы Отсюда получим равенства: Таким образом, корни задаются следующими формулами: 8

Показательная форма комплексного числа Формула Эйлера: Арифметические операции над комплексными числами в показательной форме. 1. Умножение: 2. Деление: 3. Возведение в степень: 9

Пример 3. 1) Записать число в алгебраической форме; 2) Изобразить его на координатной плоскости; 3) Записать число a в тригонометрической и показательной формах; 4) Вычислить a 5; 5) Найти все корни уравнения z 3 – a = 0. Решение. 2) 3) Число a в тригонометрической форме имеет вид: Отсюда число a в тригонометрической форме: Число a в показательной форме: 10

Пример 3 (продолжение). 5) Найдем все корни уравнения z 3 – a = 0. Запишем уравнение в виде Полагая k = 0, 1, 2, по формуле Муавра найдем: 11

Решение квадратного уравнения Рассмотрим квадратно уравнение: az 2 + bz + c = 0, a, b, c – комплексные числа и a 0. Поделим уравнение на a: Отсюда находим корни уравнения: Пусть a, b, c – действительные числа и дискриминант D < 0. Тогда Очевидно, что 12

Пример 4. Решить уравнение: x 2 – x + 1 = 0. Дискриминант D = 1 – 4 = – 3 < 0. По формуле (1) корней квадратного уравнения Пример 5. Решить уравнение: x 4 – 6 x 2 + 25 = 0. Делаем замену y = x 2: y 2 – 6 y + 25 = 0, D = 36 – 100 = – 64 < 0. Отсюда x 2 = y 1 = 3 + 4 i, т. е. 13

Пример 5 (продолжение). Для k = 0: где Для k = 1: Далее решаем уравнение x 2 = y 2 = 3 – 4 i, т. е. Решая аналогично, получим: x 3 = 2 – i, x 4 = – 2 + i. 14

Разложение многочленов Рассмотрим уравнение n-й степени ai – заданные комплексные числа, a 0 0. Основная теорема алгебры (без доказательства). Уравнение (2) имеет n в общем случае комплексных корней z 1, z 2, … , zn. Отсюда имеем: Целые неотрицательные числа ki называются кратностями корней, причем их сумма 15