Комплексные числа Лекция 1 Понятие комплексного числа

Комплексные числа Лекция 1

Понятие комплексного числа Х+А=В - недостаточно положительных Х+5=2 чисел А·Х + В=0 (А≠ 0) – разрешимы на множестве рац. чисел Х²=2 или Х³=5 - корни - иррациональные числа

Рациональные числа Иррациональные числа Действительные числа

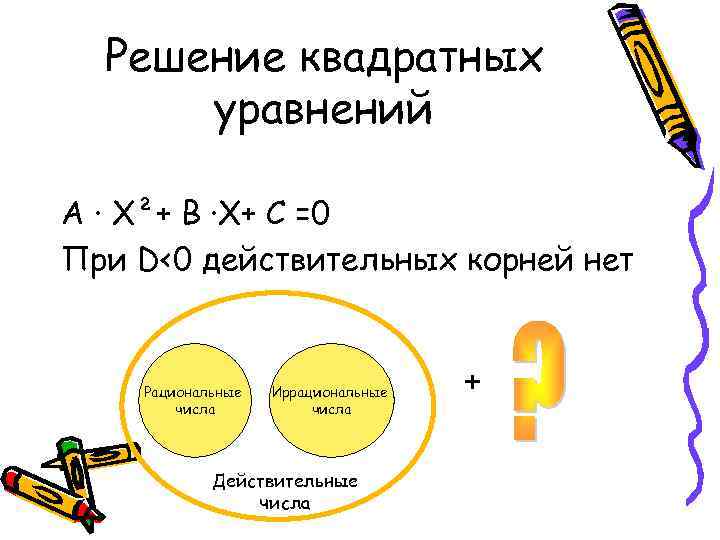Решение квадратных уравнений А · Х²+ В ·Х+ С =0 При D<0 действительных корней нет Рациональные числа Иррациональные числа Действительные числа +

Рациональные числа Иррациональные числа + Действительные числа Комплексные числа

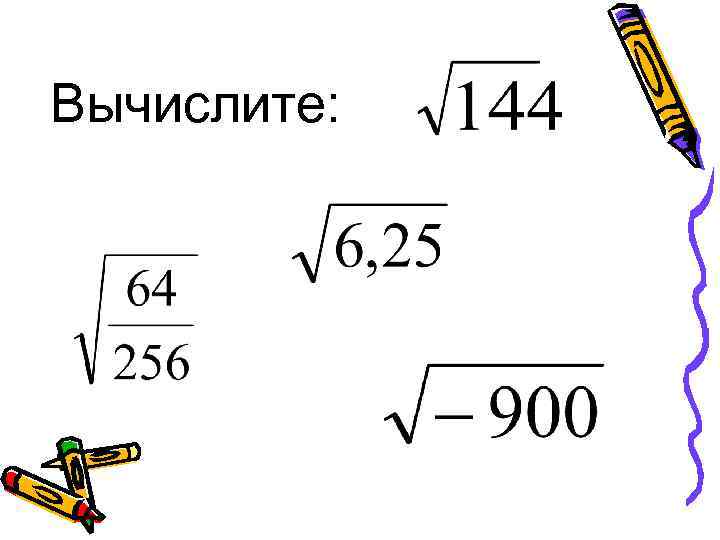Вычислите:

Вид комплексного числа ²=-1 Х=i -корень уравнения i- комплексное число, такое , что i²=-1 Х Комплексное число z можно определить как упорядоченную пару вещественных чисел (x, y). А + В· i ЗАПИСЬ КОМПЛЕКСНОГО ЧИСЛА В ОБЩЕМ ВИДЕ

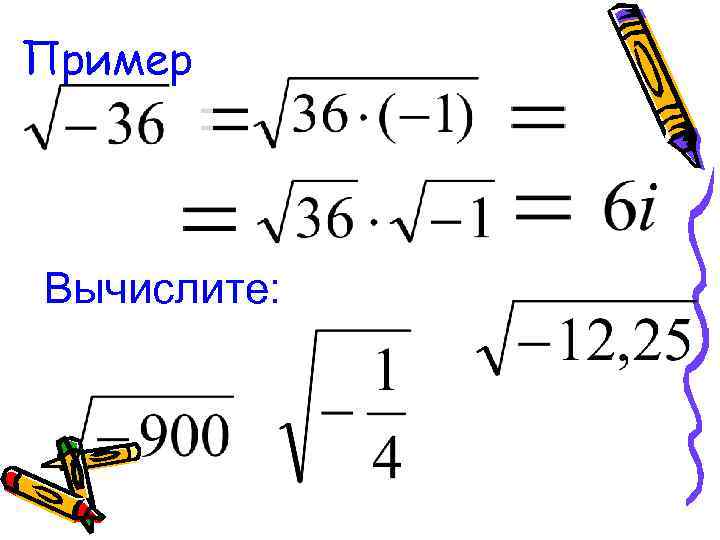Пример Вычислите:

Мнимая единица i – начальная буква французского слова imaginaire – «мнимый» Комплексные числа -расширение множества вещественных чисел, обозначается С

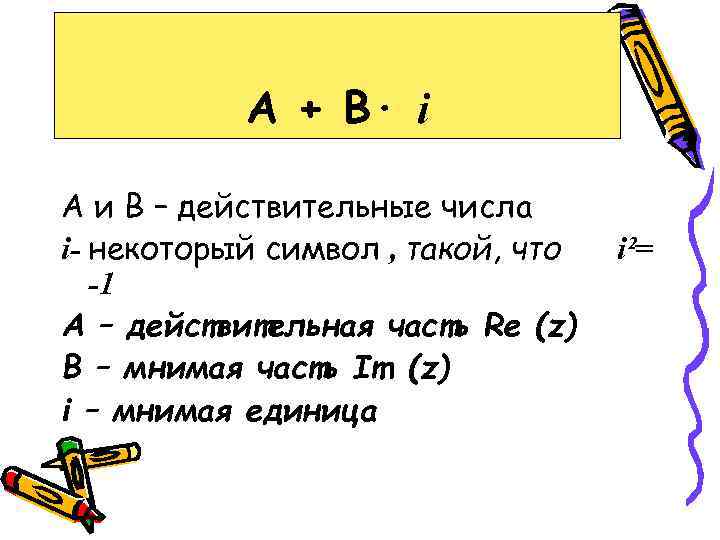А + В· i А и В – действительные числа i- некоторый символ , такой, что -1 А – действительная часть Re (z) В – мнимая часть Im (z) i – мнимая единица i²=

• Замечания • Ошибочно определение числа i как единственного числа, удовлетворяющего уравнению • так как число ( − i) также удовлетворяет этому уравнению.

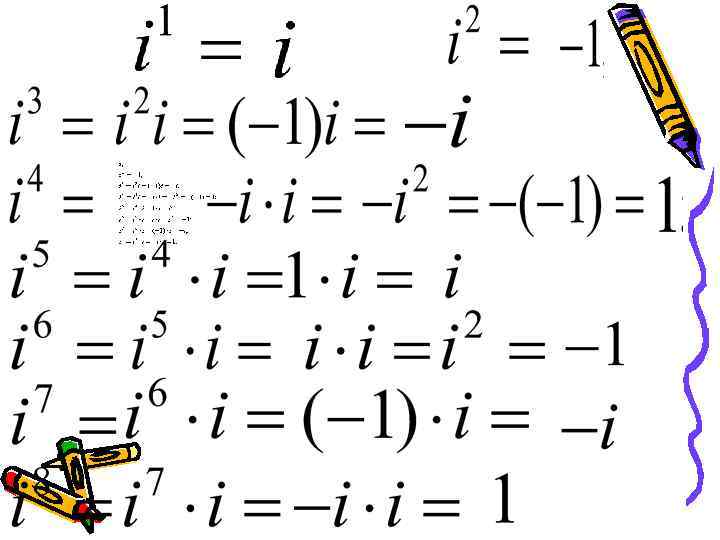
Значения степеней числа i повторяются с периодом, равным 4. Найдем:

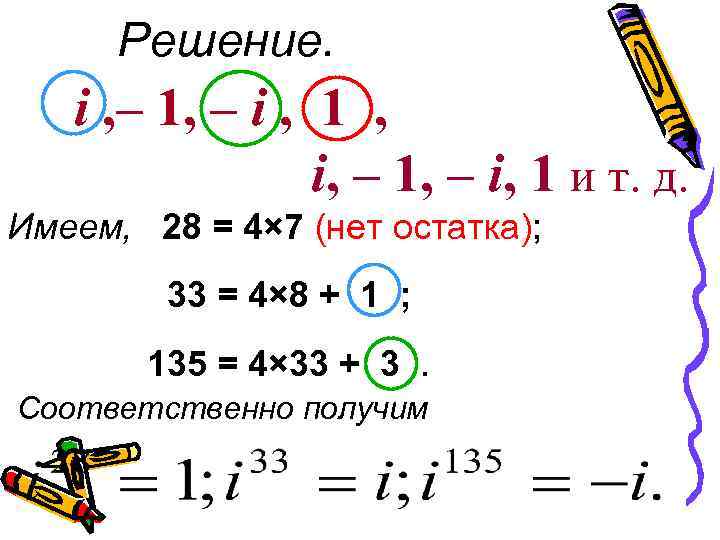Решение. i , – 1, – i , 1 , i, – 1, – i, 1 и т. д. Имеем, 28 = 4× 7 (нет остатка); 33 = 4× 8 + 1 ; 135 = 4× 33 + 3 . Соответственно получим

Комплексные числа Определение 1. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными. a - действительная часть комплексного числа, bi – мнимая часть комплексного числа, b – коэффициентом при мнимой части.

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. Первым учёным, предложившим ввести числа новой природы, был Джорж Кордано.

Он предложил Кордано назвал такие величины “чисто отрицательными” или даже “софистически отрицательными”, считая их бесполезными и стремился не применять их.

в 1572 году итальянский учёный Бомбелли выпустил книгу, в которой были установлены первые правила арифметических операций над комплексными числами, вплоть до извлечения из них кубических корней.

в 1637 году Название “мнимые числа” ввёл французский математик и философ Р. Декарт

в 1777 году один из крупнейших математиков XVIII века – Л. Эйлер предложил использовать первую букву французского слова imaginare (мнимый)

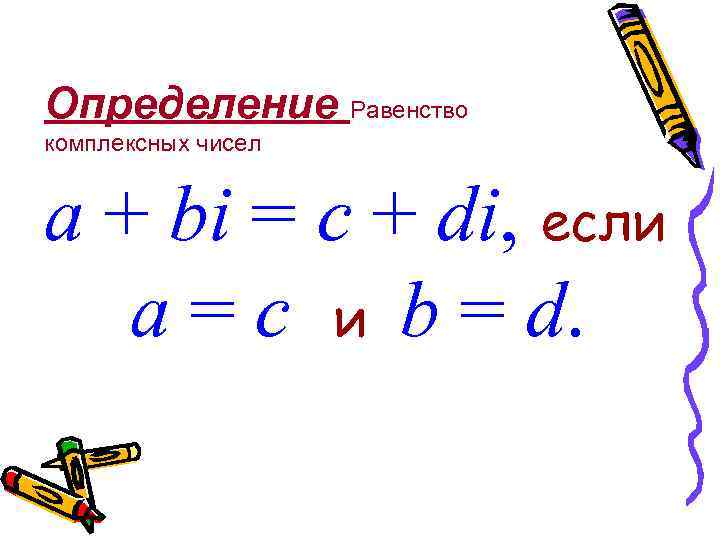Определение Равенство комплексных чисел a + bi = c + di, если a = c и b = d.

Пример Найти x и y из равенства: 3 y + 5 xi = 15 – 7 i; Решение. Согласно условию равенства комплексных чисел 3 y = 15, 5 x = – 7. Отсюда имеем

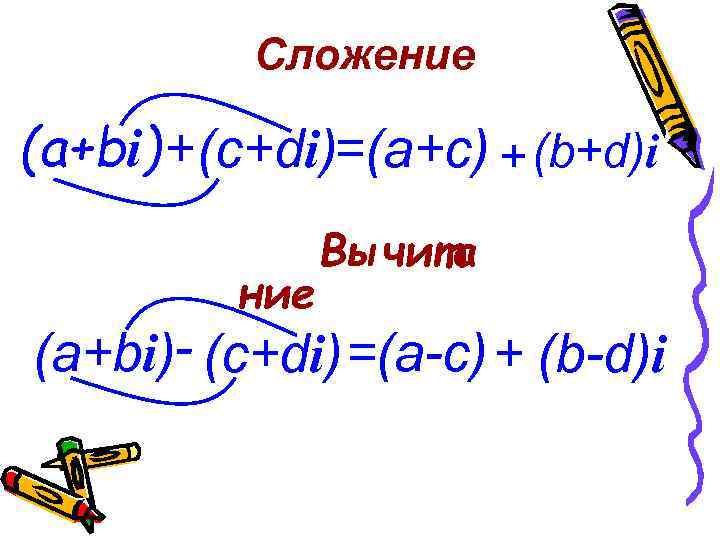Сложение (а+bi) +(c+di)=(a+c) + (b+d)i ние Вычита (а+bi)- (c+di) =(a-c) + (b-d)i

Выполните действия: z 1 = 2 + 3 i, z 2 = 5 – 7 i. Найти: а) z 1 + z 2; б) z 1 – z 2; Решение. а) z 1 + z 2 =(2 + 3 i) + (5 – 7 i) = =(2 + 5) + (3 i – 7 i) = 7 – 4 i; б) z 1 – z 2 =(2 + 3 i) – (5 – 7 i) = =(2 – 5) + (3 i + 7 i) = – 3 + 10 i;

Умножение комплексных чисел (а+bi)(c+di) = = ac + аd i + bс i + 2 bd i = (ac-bd) + (аd+bc)i =

Выполните действия: (2 + 3 i)(5 – 7 i) = = (10+21) + (-14+15)i = 31+i (5 + 3 i)(5 – 3 i) 25 -9 i 2 = 34 = 2 (2 – 7 i) = 4 - 28 i + =-45 -28 i 2 -16 i 2 = 2+16 25 m = (5 m-4 i)(5 m+4 i) 2 49 i

Геометрическая интерпретация комплексного числа Если x = 0, то z называется мнимым или чисто мнимым числом. Если y = 0, то z является действительным (вещественным) числом

Комплексно сопряженные числа Z=А - В· i СОПРЯЖЕННОЕ Z= А + В· i (Z) = Z Модуль комплексного числа Z = A + B i=

Определение Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью. z 1= a+bi и z 2=a-bi

Деление комплексных чисел = = =

Выполните действия: = = 2 =

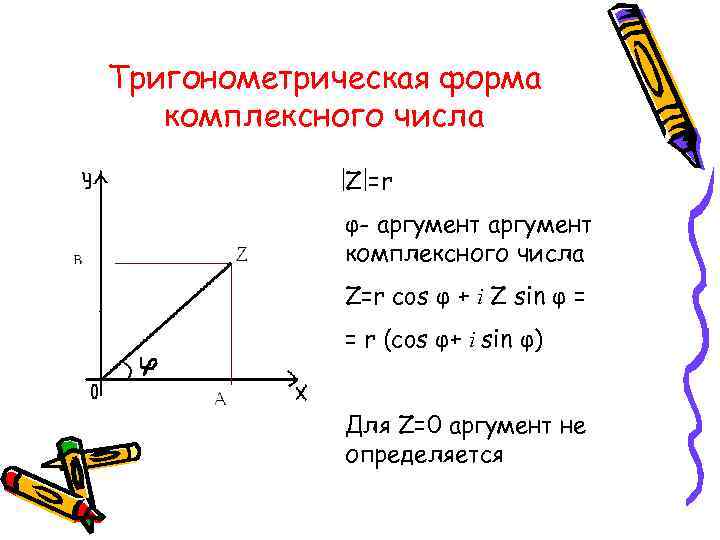Тригонометрическая форма комплексного числа Z =r φ- аргумент комплексного числа Z=r cos φ + i Z sin φ = = r (cos φ+ i sin φ) Для Z=0 аргумент не определяется

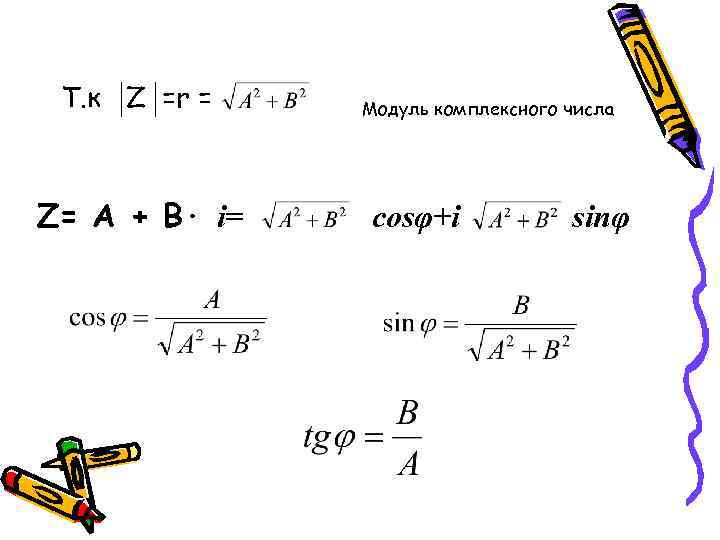Т. к Z =r = Модуль комплексного числа Z= А + В· i= cosφ+i sinφ

Аргумент комплексного числа Для нуля значение аргумента не определено, для ненулевого числа z аргумент определяется с точностью до 2 kπ, где k — любое целое число Угол (в радианах) радиус-вектора точки, соответствующей числу z, называется аргументом числа z . Главным значением аргумента Свойства аргумента

Сложение и умножение комплексных чисел Алгебраическая форма Сумма (A+i. B) + (C+i. D)= (A+C)+(B+D)I Произведение (A+i. B) · (C+i. D)= (AC-BD)+(AD+BC)i Тригонометрическая форма Произведение Z 1= r 1 (cos φ1+ i sin φ1) Z 2= r 2(cos φ2+ i sin φ2) Z 1 ·Z 2= r r 2[cos( φ + φ )+isin ( φ + φ )] 1 1 2

Если Z 1= Z 2, то получим Z²=[r (cos φ+ i sin φ)]²= =r² (cos 2 φ+ i sin 2φ) Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+ i sin φ)= = r³ (cos 3 φ+ i sin 3φ) Формула Муавра Для любого Z= r (cos φ+ i sin φ)≠ 0 и любого натурального числа n

Число Z называется корнем степени n из числа ω (обозначается ), если (*) Из данного определения вытекает, что каждое решение уравнения является корнем степени n из числа ω. Z= r (cos φ+ i sin φ) ω= ρ(cos ψ+ i sin ψ) Вторая формула Муавра

Вторая формула Муавра определяет все корни двучленного уравнения степени n Теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайне мере один корень Каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел ровно n-корней.

Корни из единицы

Пример: Решить уравнение:

Свойства сложения и умножения Переместительное свойство: Z 1 + Z 2 = Z 1 + Z 2 Z 1 · Z 2 = Z 1 · Z 2 Сочетательное свойство: (Z 1 + Z 2 )+Z 3 = Z 1 +(Z 2+Z 3) (Z 1 · Z 2 ) · Z 3 = Распределительные свойство: Z 1 ·(Z 2 + Z 3 )= Z 1 · Z 2+ Z 1 · Z 3 Z 1 ·(Z 2 · Z 3)

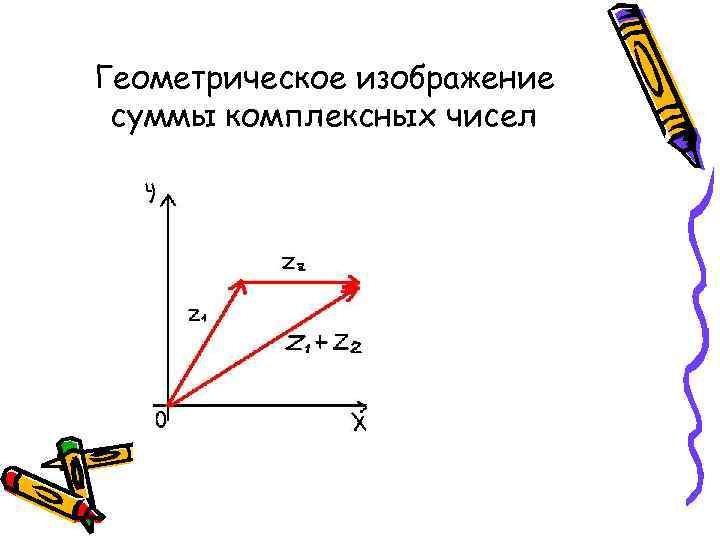Геометрическое изображение суммы комплексных чисел

Вычитание и деление комплексных чисел Вычитание – операция, обратная сложению: Z+ Z 2 = Z 1 Z+ Z 2 +(- Z 2 )= Z 1 +(- Z 2 ) Z= Z 1 - Z 2 –разность Деление – операция, обратная умножению: Z · Z 2 = Z 1 Разделив обе части на Z получим: 2

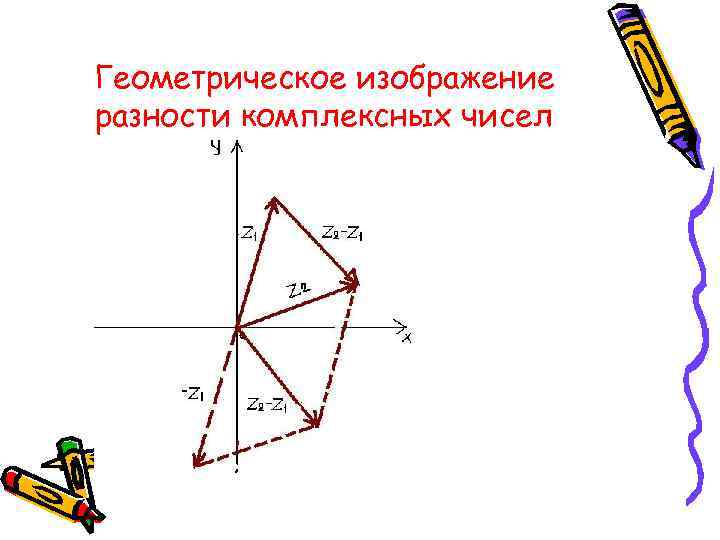Геометрическое изображение разности комплексных чисел

Примеры: Найти разность и частное комплексных чисел Решение: