Комбинированная логика Лекция 4 Схемы inputs func

Комбинированная логика Лекция 4

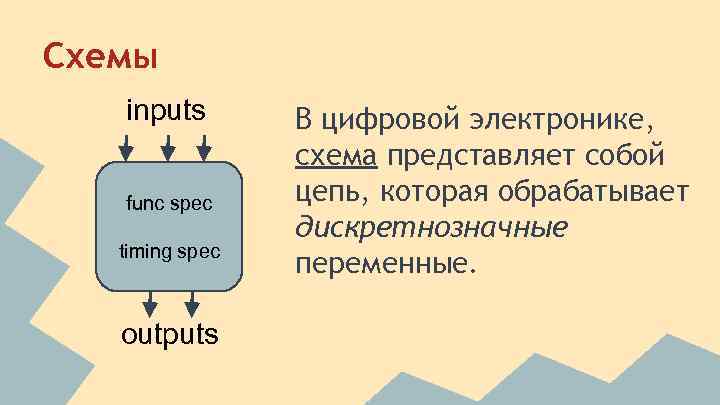
Схемы inputs func spec timing spec outputs В цифровой электронике, схема представляет собой цепь, которая обрабатывает дискретнозначные переменные.

Спецификации ● Функциональная спецификация (func spec) описывает функциональную взаимосвязь между входом и выходом ● Временная спецификация (timing spec) описывает задержку между изменениями входа и реакцией выхода

Структура схемы Схема состоит из элементов (E) и узлов (n). ● каждый элемент является схемой с входом, выходом и спецификацей ● узел - это провод, напряжение которого передает дискретнозначную переменную.

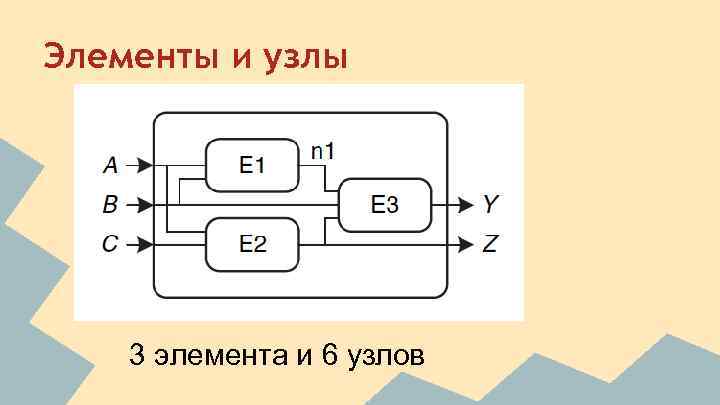
Элементы и узлы 3 элемента и 6 узлов

Узлы делятся на: ● input (входной узел) ● output (выходной узел) ● internal (промежуточный узел) Входной узел получает значение извне. Выходной узел передает значение наружу.

Цифровые схемы Ц. с. делятся на комбинированные и последовательные. В комбинированных схемах выход зависит только от текущего значения входа. В последовательных схемах выход зависит от текущего и предыдущих значений входа

Комбинированные схемы Логические пороги - являются примером комбинированных схем. У комбинированных схем нет памяти. В комбинированных схемах используется только текущее значение входа, чтобы вычислить выход

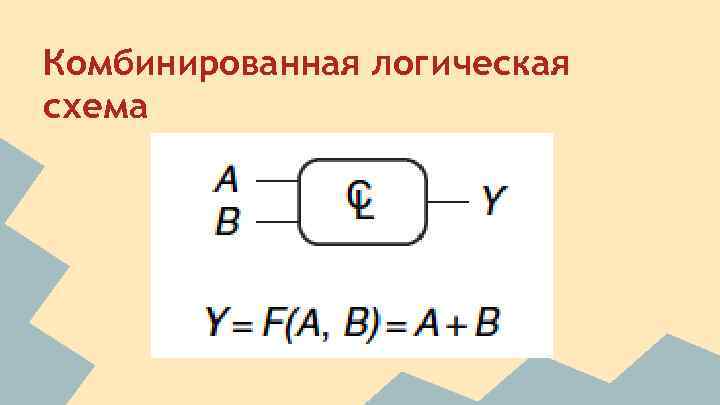
Комбинированная логическая схема

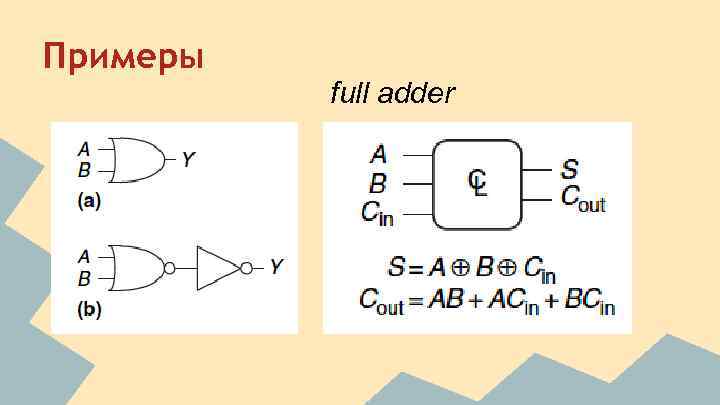
Примеры full adder

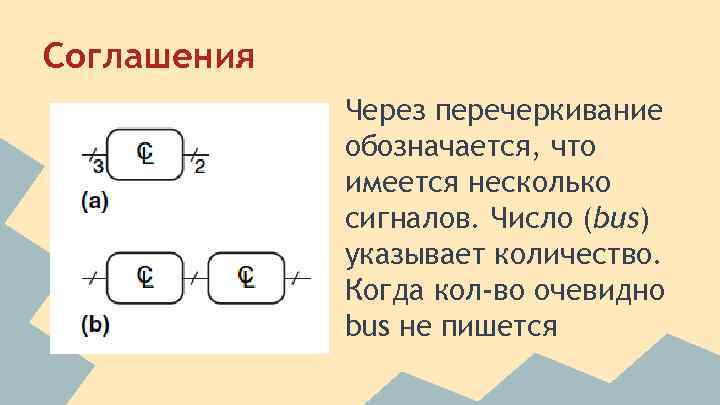
Соглашения Через перечеркивание обозначается, что имеется несколько сигналов. Число (bus) указывает количество. Когда кол-во очевидно bus не пишется

Комбинированная схема ● схема комбинирована, если каждый элемент схемы комбинирована ● каждый узел соединяется как вход к схеме или как выход из элемента только один раз ● в схеме нет циклов: каждый путь проходит через один узел только один раз

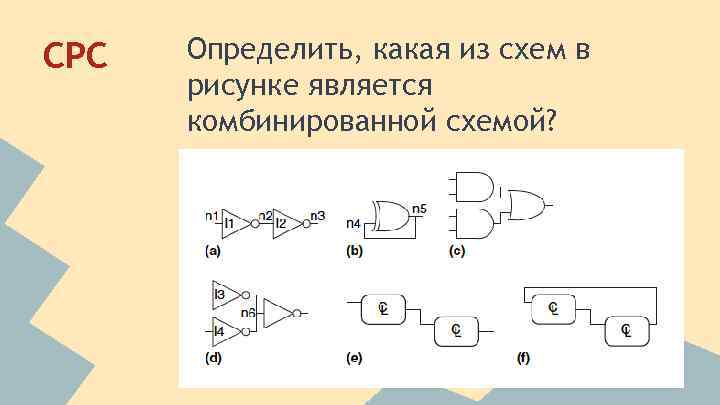
СРС Определить, какая из схем в рисунке является комбинированной схемой?

СРС В предыдущем рисунке для каждой схемы определите количество элементов и узлов. Сколько входных, выходных и промежуточных узлов?

Булевые уравнения

Терминология A переменная. Ā - дополнение переменной A, Ā - называются литералами А - истинная форма переменной Ā - дополнительная форма переменной

Минтермы AND между литералами называется произведение или импликантой Например, ĀBC, ĀB Минтерм (minterm) - произведение, в котором участвуют все входы Например, ĀBC - минтерм, а BC не минтерм, т. к. вход A не участвует

Макстермы OR между литералами называется сумма (sum) Макстермы - это сумма, где участвуют все входы. Например, Ā + B + C

Порядок выполнения операции В булевых выражениях имеет значение порядок выполнения операций: NOT выполняется первой AND второй OR после

Булевое уравнение можно представить с помощью суммы из минтермов. Из таблицы истинности выбираются минтермы, которые находятся напротив значений Y = 1 и суммируются

Таблица истинности и Минтермы Y = ĀB + AB Минтермы принимают значение TRUE Y = ĀB

Каноническая форма Представление булевого уравнения в виде суммы минтермов называется канонической, или стандартная форма, или КНФ коньюктивная нормальная форма Sum-of-products сумма произведений.

Каноническая форма Сигма нотация: F(A, B) = ⅀(m 1, m 3) или F(A, B) = ⅀(1, 3)

СРС. Пикник Айбек счастлив, когда во время пикника не будет дождя и муравьев. Составить схему, которая выдает TRUE, тогда и только тогда, когда Айбек счастлив.

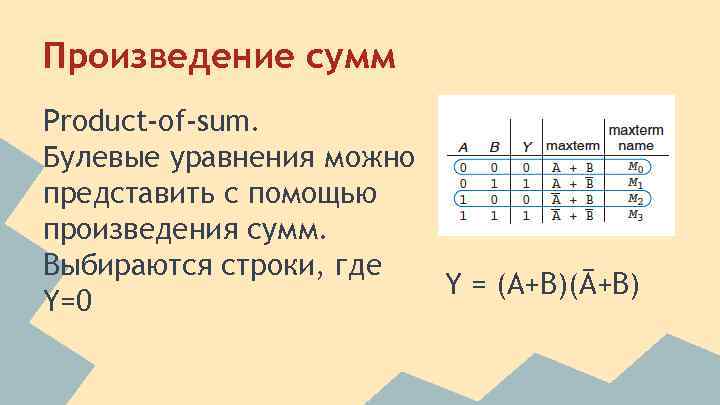
Произведение сумм Product-of-sum. Булевые уравнения можно представить с помощью произведения сумм. Выбираются строки, где Y = (A+B)(Ā+B) Y=0

CPC В задании Пикник составьте канонические формы булевых уравнений в виде 1. sum-of-product 2. product-of-sum

Булева алгебра Булевые уравнения можно сокращать. Для этого используется булева алгебра. Имеются несколько аксиом, на которых основывается булева алгебра.

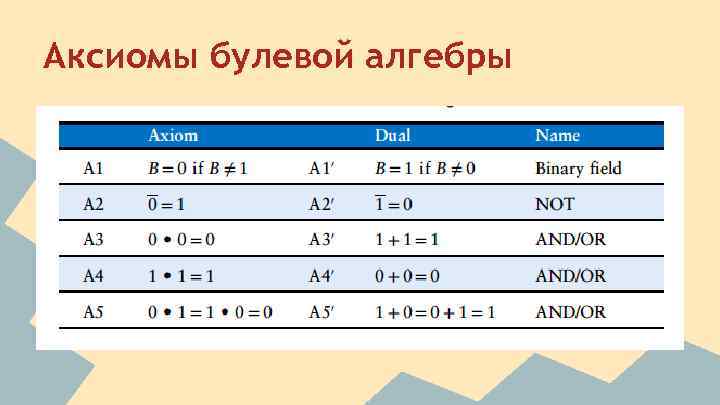
Аксиомы булевой алгебры

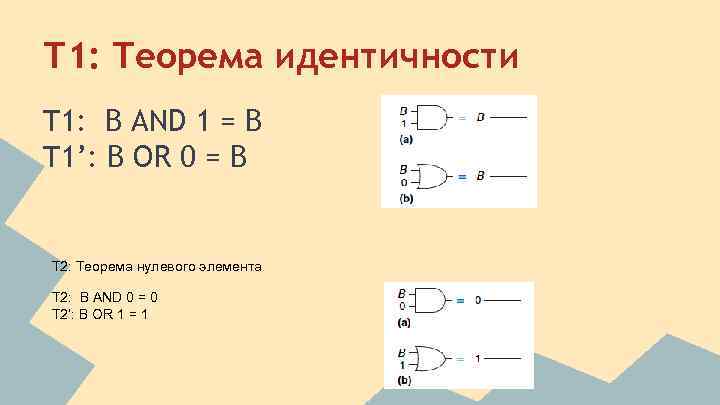
Т 1: Теорема идентичности T 1: B AND 1 = B T 1’: B OR 0 = B T 2: Теорема нулевого элемента T 2: B AND 0 = 0 T 2’: B OR 1 = 1

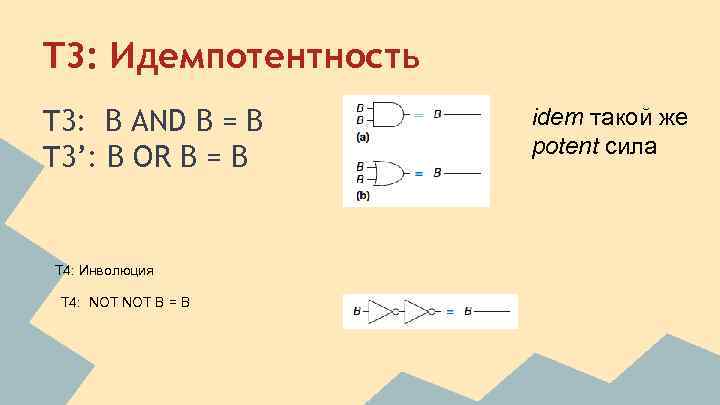
T 3: Идемпотентность T 3: B AND B = B T 3’: B OR B = B T 4: Инволюция T 4: NOT B = B idem такой же potent сила

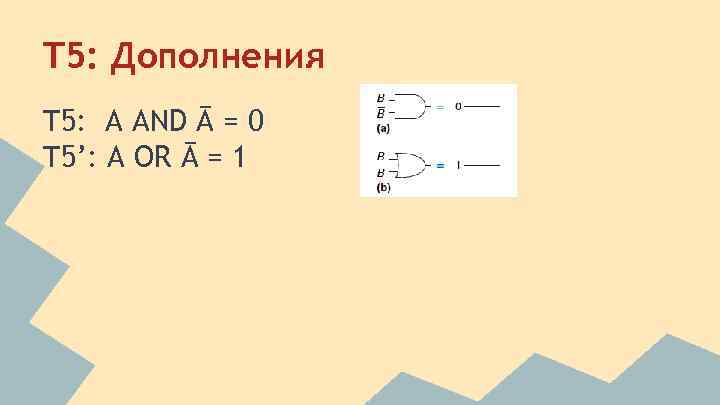
T 5: Дополнения T 5: A AND Ā = 0 T 5’: A OR Ā = 1

Теоремы нескольких переменных

T 12: Теорема де Моргана очень полезная для упрощения схем. Дополнение произведений равно сумме дополнений Дополнение сумм равно произведению дополнений

Следствие теоремы де Моргана NAND равно OR дополнений входов NOR равно AND дополнений входов Процесс инверсии называется эффект пузыря (bubble) потому что кружочек в схеме выплывает на начало ворот

Правила движения пузыря ● Движение пузыря вперед [от входа] или назад [от выхода] меняет тело схемы с AND на OR, или наоборот ● Движение пузыря назад от выхода к входам ставит пузыри на все входы ● Движение всех пузырей с входов к выходу ставит пузырь у выхода

СРС Используя теорему де Моргана вывести каноническую форму произведений сумм Y от суммы произведений NOT Y

Доказательство теорем В Булевой алгебре доказательство теорем сводится к тому, что нужно перебирать все возможные значения в таблице истинности и применить метод совершенной индукции. Такой способ доказательства возможно, поскольку мы имеем дело с конечным числом переменных и значений.

Сокращение уравнений Применяя Т 10 следующее уравнение можно сократить до

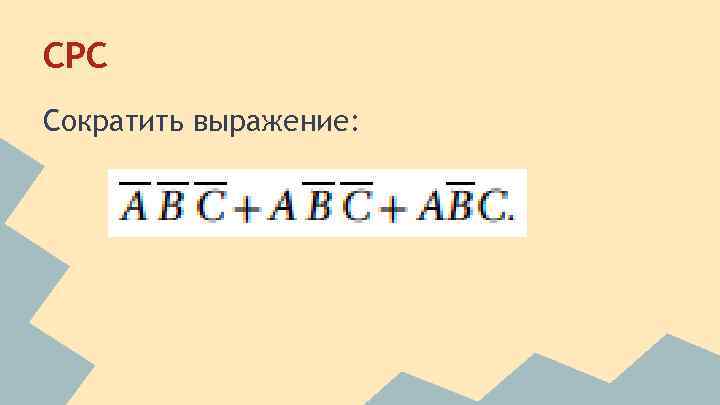
СРС Сократить выражение:

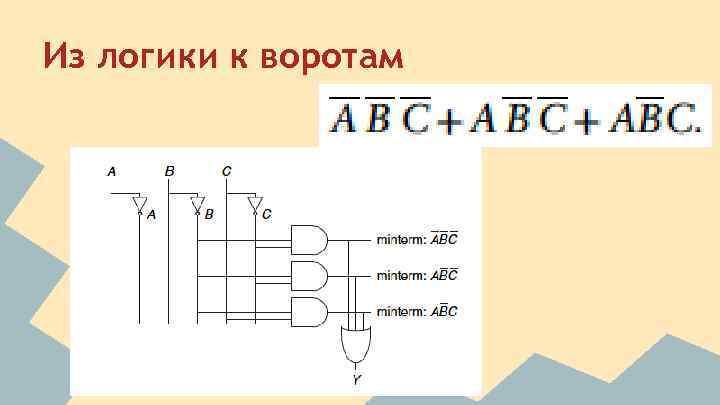
Из логики к воротам

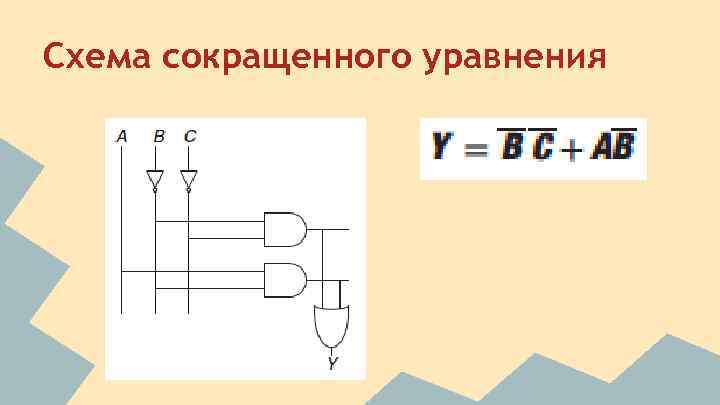
Схема сокращенного уравнения

Правила построения схем ● Входы находятся слева или сверху схемы ● Выходы находятся справа или снизу ● Когда возможно ворота смотрят слева направо ● Проводы всегда прямые

Пересечения Провода продолжаются всегда через Т переход Точка в перечений проводов означает, что провода соединены Пересечение линий без точки означает, провода не пересекаются

СРС: Актовый зал Участники: декан [Киричок], замдекана [Ашимова], преподаватель [Сержан], председатель студ. совета [Шанин] Участники время от времени конфликтуют по поводу использования Актового зала Нужно составить схему решения задачи резервирования Актового зала

СРС: Актовый зал [продолжение] Киричок обладает высоким, Ашимова средним, Сержан - ниже средним, Шанин низким приоритетами В системе 4 входа A 3, A 2, A 1, A 0 и 4 выхода Y 3, Y 2, Y 1, Y 0. Можно записать: A 3: 0 и Y 3: 0. Каждый участник вводит свое значение за день до резерва зала

СРС: Актовый зал [продолжение] Схема должна выводить ответ, о том, что зал зарезервирован участнику с наибольшим приоритетом из тех, кто подал заявку.

CPC: Два охранника: рай или ад Один врет, другой говорит правду. Задается вопрос любому: на какую дверь покажет другой охранник, если я спрошу “где дверь в рай? ” Получив ответ, нужно пойти в другую дверь, чтобы попасть в рай Составить схему данного процесса.