Комбинация призмы и цилиндра Смышляев Н.
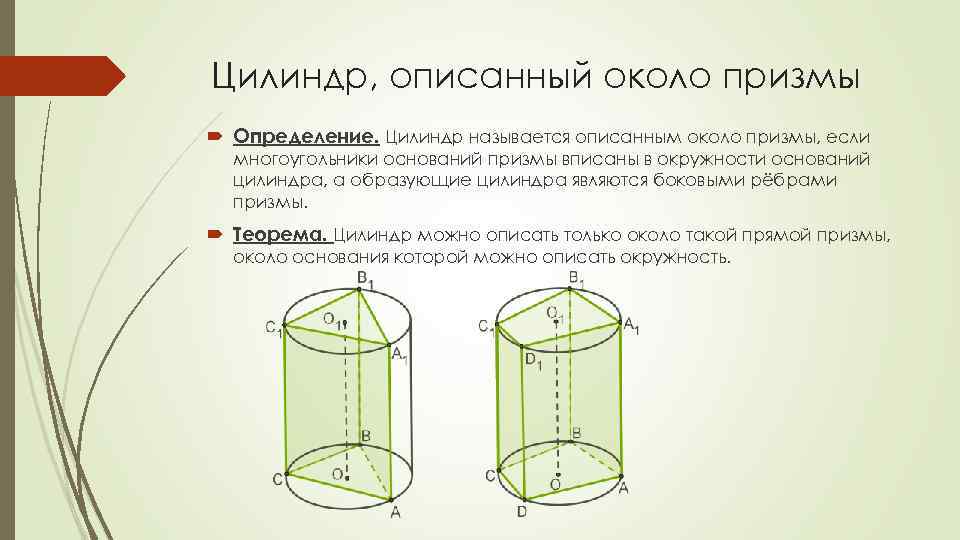
Цилиндр, описанный около призмы Определение. Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы. Теорема. Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность.
Свойства Окружность основания цилиндра описана около многоугольника основания призмы. Радиус цилиндра — это радиус окружности, описанной около многоугольника основания призмы.
Свойства Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника. Центр окружности, описанной около четырёхугольника, является точкой пересечения серединных перпендикуляров к сторонам четырёхугольника. Около четырёхугольника можно описать окружность, если суммы противоположных углов равны 180°.
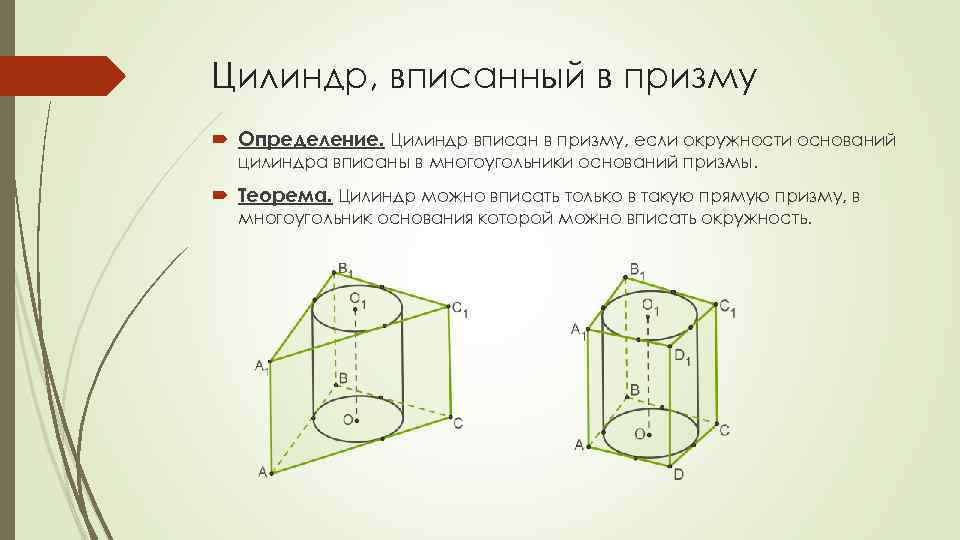
Цилиндр, вписанный в призму Определение. Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы. Теорема. Цилиндр можно вписать только в такую прямую призму, в многоугольник основания которой можно вписать окружность.
Свойства Окружность основания цилиндра вписана в многоугольник основания призмы. Радиус цилиндра — радиус окружности, вписанной в многоугольник основания призмы.
Свойства Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника. Центр окружности, вписанной в четырёхугольник, находится в точке пересечения биссектрис четырёхугольника. В четырёхугольник можно вписать окружность, если равны суммы длин противоположных сторон.
Скачать презентацию Комбинация призмы и цилиндра Смышляев Н Цилиндр
Комбинация призмы и цилиндра, Смышляев.pptx