4559_1.ppt
- Количество слайдов: 32

Комбінації геометричних тіл Кириченко Лариса Миколаївна, вчитель математики Черкаська гімназія № 31

Приклади комбінації фігур

Можливі типи комбінацій геометричних тіл 1. Многогранник і многогранник (призма вписана в піраміду, або піраміда вписана в призму, та інші) 2. Многогранник і тіло обертання (піраміда вписана в конус або циліндр або кулю; циліндр, вписаний в піраміду або призму; куля вписана або описана навколо піраміди та інші. ) 3. Тіло обертання і тіло обертання (конус вписаний в циліндр, куля описана навколо циліндра, та інші. )
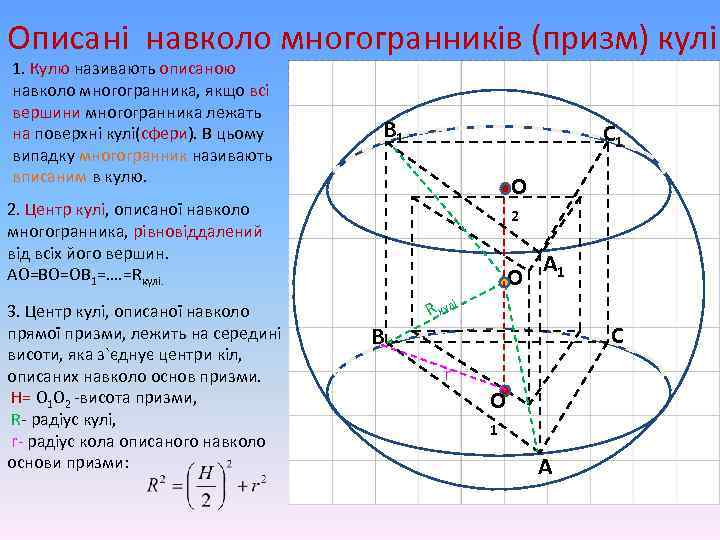
Описані навколо многогранників (призм) кулі 1. Кулю називають описаною навколо многогранника, якщо всі вершини многогранника лежать на поверхні кулі(сфери). В цьому випадку многогранник називають вписаним в кулю. В 1 С 1 О 2. Центр кулі, описаної навколо многогранника, рівновіддалений від всіх його вершин. АО=ВО=ОВ 1=…. =Rкулі. 3. Центр кулі, описаної навколо прямої призми, лежить на середині висоти, яка з`єднує центри кіл, описаних навколо основ призми. H= О 1 О 2 -висота призми, R- радіус кулі, r- радіус кола описаного навколо основи призми: 2 О А 1 R кулі С В r О 1 А

Описані навколо многогранників (призм) кулі (продовження) 1. Кулю можна описати навколо призми, тільки якщо вона пряма і її основа многокутник навколо якого можна описати коло. B 1 Кулю можна описати навколо призми якщо в основі лежить прямокутник, квадрат. 2. Центр кулі, описаної навколо прямокутного паралелепіпеда, лежить в точці перетину діагоналей паралелепіпеда, а кожна його діагональ є діаметром описаної кулі. АС 1=dкулі=2 R C 1 D A 1 1 О C B A D
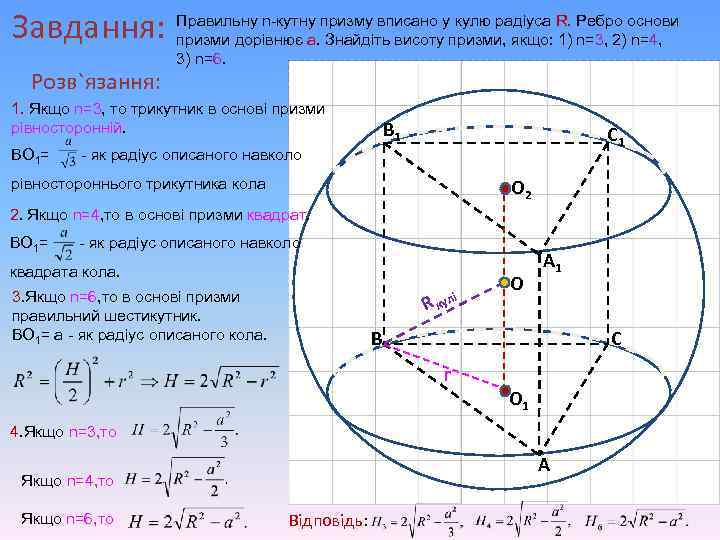
кулю радіуса Завдання: Правильну n-кутну призму вписано упризми, якщо: R. Ребро основи призми дорівнює а. Знайдіть висоту 1) n=3, 2) n=4, Розв`язання: 3) n=6. 1. Якщо n=3, то трикутник в основі призми рівносторонній. ВО 1= В 1 С 1 - як радіус описаного навколо рівностороннього трикутника кола О 2 2. Якщо n=4, то в основі призми квадрат. ВО 1= - як радіус описаного навколо квадрата кола. 3. Якщо n=6, то в основі призми правильний шестикутник. ВО 1= а - як радіус описаного кола. R і кул О А 1 В С r О 1 4. Якщо n=3, то А Якщо n=4, то Якщо n=6, то Відповідь:

Вписані в многогранники (призми) кулі 1. Кулю можна вписати в пряму призму, якщо її основи є многокутниками, описаними навколо кола, а висота В 1 призми дорівнює діаметру кулі і діаметру цього кола. 2. Центр кулі, вписаної в пряму призму, лежить на середині відрізка, який з’єднує центри кіл, вписаних в основи призми. 3. Радіус кулі дорівнює радіусу кола, вписаного в основу призми, а діаметр кулі дорівнює висоті призми. С 1 О 2 А 1 О В 4. R-радіус кулі, r- радіус кола, вписаного в основу призми, H = О 1 О 2 - висота призми і діаметр кулі. R С О 1 r А

Завдання: 6 см Знайдіть радіус кулі, вписаної в куб з ребром 6 см. Розв`язання: 1. Будуємо переріз куба. A 6 см О 2 C О 2 B B О О R D О 1 C 2. Радіус вписаної кулі дорівнює радіусу вписаного в квадрат АВСD кола: R=О 1 О 2: 2 = 6: 2 = =3(см) Відповідь: R=3 см. D О 1 A

Описані навколо пірамід кулі 1. Кулю називають описаною навколо піраміди, якщо всі вершини піраміди лежать на поверхні кулі. 2. О 1 - центр кулі; АО 1=Rкулі ; О центр кола описаного навколо основи. 3. Центр кулі, описаної навколо довільної піраміди лежить на прямій, перпендикулярній площині основи, яка проходить через центр кола, описаного навколо основи, в точці перетину цієї прямої з площиною, яка перпендикулярна до бічного ребра і проходить через його середину. ОО 1 ┴ (АВС); М - середина SA; α ┴ SA(М α ); α перетинає ОО 1 в точці О 1. 4. Центр кулі може знаходитись: • в середині піраміди; • в площині основи; • поза пірамідою. S М О 1 B Rкулі О A C

Описані навколо пірамід кулі (продовження) 1. Якщо вершина піраміди проектується в центр кола описаного навколо основи, то центр описаної кулі лежить на прямій, яка містить висоту піраміди в точці перетину цієї прямої з серединним перпендикуляром до бічного ребра. SO - висота піраміди; О-центр кола описаного навколо основи піраміди; АО = r - радіус кола описаного навколо основи піраміди; М-середина ребра SА, МО 1∩SА=О 1 -центр описаної кулі 2. Якщо центр описаної кулі лежить на висоті піраміди або на її продовженні, то при розв`язанні деяких задач можна продовжити висоту піраміди до перетину з кулею в точці S 1 і з`єднати S 1 з А. Тоді SS 1 діаметр кулі SAS 1 - прямий, як вписаний кут, який спирається на діаметр. S R M О 1 C B О A ┐ r D S 1

Завдання: Доведіть, що центр кулі, описаної навколо правильної піраміди, лежить на її осі. Розв`язання: 1. Точка О-центр описаної кулі Опустимо перпендикуляр ОА з центра кулі на площину основи піраміди. О 2. Нехай Х - довільна вершина основи піраміди. 3. За теоремою Піфагора АХ 2=ОХ 2 -ОА 2=R 2 -OA 2. Таким чином, АХ одне і те саме для будь -якої вершини основи піраміди. А це означає, що точка А є центром кола, описаного навколо основи піраміди. Отже центр кулі лежить на осі піраміди, що і потрібно було довести. R А Х
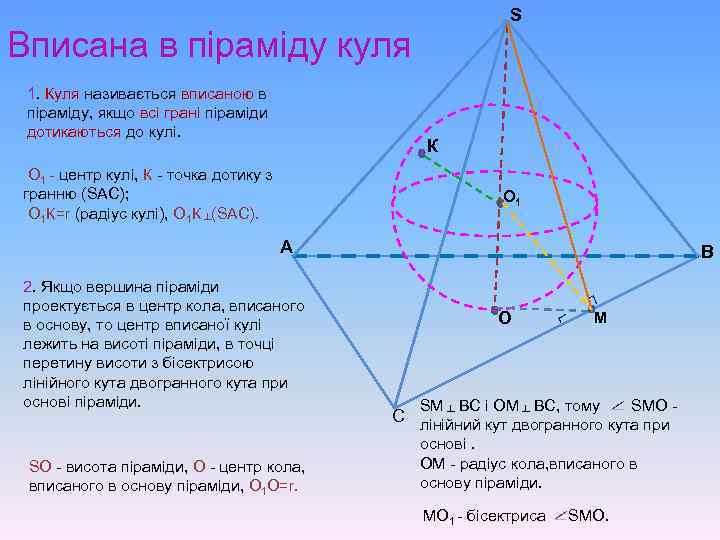
S Вписана в піраміду куля 1. Куля називається вписаною в піраміду, якщо всі грані піраміди дотикаються до кулі. К О 1 - центр кулі, К - точка дотику з гранню (SАС); О 1 К=r (радіус кулі), О 1 К ┴(SАС). О 1 А SО - висота піраміди, О - центр кола, вписаного в основу піраміди, О 1 О=r. ┐ О ┐ 2. Якщо вершина піраміди проектується в центр кола, вписаного в основу, то центр вписаної кулі лежить на висоті піраміди, в точці перетину висоти з бісектрисою лінійного кута двогранного кута при основі піраміди. В M SM ВС і ОМ ВС, тому SМО - ┴ ┴ С лінійний кут двогранного кута при основі. ОМ - радіус кола, вписаного в основу піраміди. МО 1 - бісектриса SМО.

Завдання: S Висота правильної чотирикутної піраміди 3 см. Апофема утворює з площиною основи кут 60°. З найдіть радіус кулі вписаної в піраміду. Розв`язання: 1. SO=H=6 см - висота піраміди; О 1 - центр вписаної кулі; О 1 О = r радіус вписаної кулі; SМО=60º. SМО, тому 3. Із прямокутного трикутника ОSM ОM=SOctg 60°= (cм). 4. Із прямокутного трикутника ОО 1 M ОО 1=МOtg 30°= 1(cм). О 60º ┐ 2. МО 1 - бісектриса О 1 МО=30º. О 1 ┐ M Відповідь: r = 1 см.
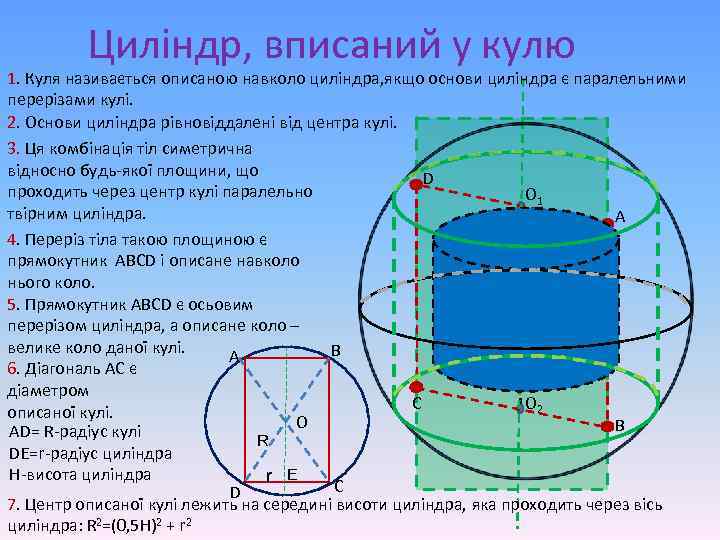
Циліндр, вписаний у кулю 1. Куля називається описаною навколо циліндра, якщо основи циліндра є паралельними перерізами кулі. 2. Основи циліндра рівновіддалені від центра кулі. 3. Ця комбінація тіл симетрична відносно будь-якої площини, що D проходить через центр кулі паралельно О 1 твірним циліндра. А 4. Переріз тіла такою площиною є прямокутник АВСD і описане навколо нього коло. 5. Прямокутник АВСD є осьовим О перерізом циліндра, а описане коло – велике коло даної кулі. B А 6. Діагональ АС є діаметром С О 2 описаної кулі. О В AD= R-радіус кулі R DE=r-радіус циліндра H-висота циліндра r E С D 7. Центр описаної кулі лежить на середині висоти циліндра, яка проходить через вісь циліндра: R 2=(0, 5 H)2 + r 2

Завдання: У кулю вписано рівносторонній циліндр(висота циліндра дорівнює його діаметру). У скільки разів площа великого круга кулі більша за площу основи циліндра? Розв`язання: А О 1 В 1. АВ=О 1 О 2=Нц=2 rц 2. S осн. ц. =π rц2 О 3. Із прямокутного рівнобедреного трикутника ОО 1 В ОВ=Rк= rц 4. Sк=π (rц ) 2 = 2π rц2 5. Sк: Sос. ц. =( 2π rц2): ( π rц2)=2 Відповідь: у 2 рази. О 2
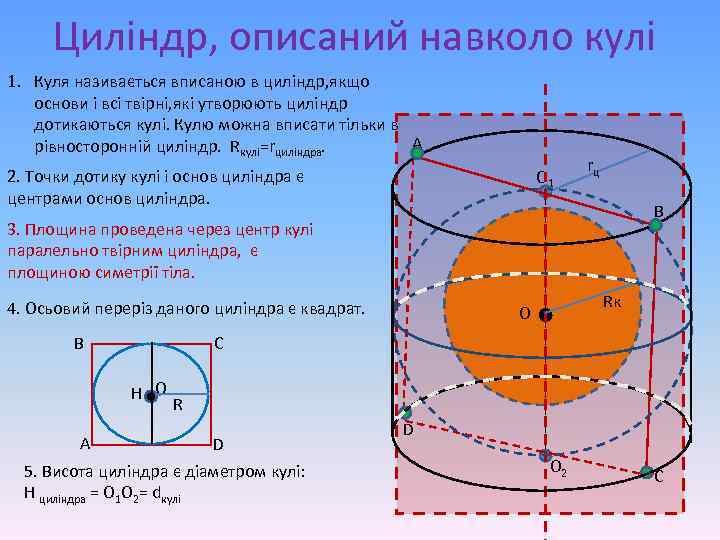
Циліндр, описаний навколо кулі 1. Куля називається вписаною в циліндр, якщо основи і всі твірні, які утворюють циліндр дотикаються кулі. Кулю можна вписати тільки в A рівносторонній циліндр. Rкулі=rциліндра. 2. Точки дотику кулі і основ циліндра є центрами основ циліндра. О 1 rц B 3. Площина проведена через центр кулі паралельно твірним циліндра, є площиною симетрії тіла. 4. Осьовий переріз даного циліндра є квадрат. B C H О A Rк О R D 5. Висота циліндра є діаметром кулі: Н циліндра = О 1 О 2= dкулі D О 2 C
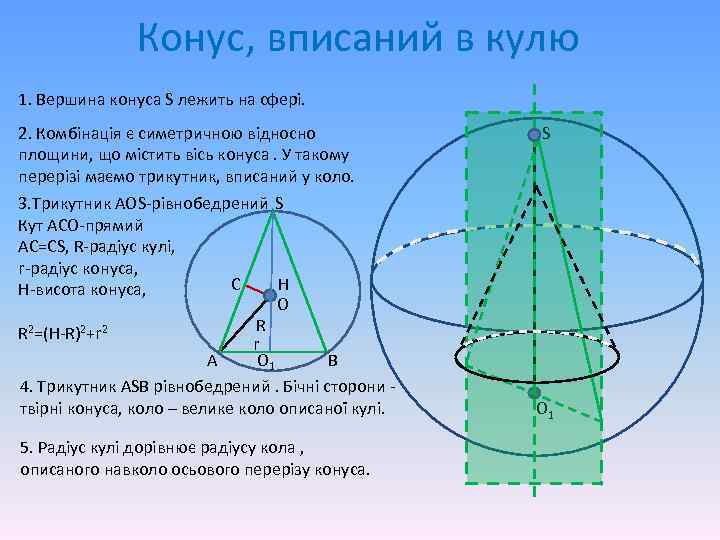
Конус, вписаний в кулю 1. Вершина конуса S лежить на сфері. 2. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі маємо трикутник, вписаний у коло. 3. Трикутник АОS-рівнобедрений S Кут АСО-прямий АС=СS, R-радіус кулі, r-радіус конуса, C H H-висота конуса, О R R 2=(H-R)2+r 2 r В O 1 А 4. Трикутник ASB рівнобедрений. Бічні сторони твірні конуса, коло – велике коло описаної кулі. 5. Радіус кулі дорівнює радіусу кола , описаного навколо осьового перерізу конуса. S O 1

Завдання: У рівносторонній циліндр вписано кулю радіуса R, а в неї вписано рівносторонній конус(осьовий переріз конуса – правильний трикутник). Знайдіть відношення площ бічних поверхонь циліндра і конуса. О 1 А Розв`язання: 1. Будуємо осьовий переріз циліндра. 2. R- радіус 2 rконуса описаного навколо рівностороннього R r конуса трикутника із стороною 2 rконуса R= 3. Sц =2πRH=4πR 2= πr 2 4. Sк=πrl=2πr 2 5. Sц: Sк=8: 3 Відповідь: 8: 3. О В О 3 С О 2

Куля , вписана в конус 1. Кулю можна вписати в будь-який конус. Куля дотикається основи конуса в його центрі і бічної поверхні конуса по колу, що лежить в площині, паралельній основі конуса. S 2. Площина, яка містить вісь конуса, є площиною симетрії. 3. Осьовий переріз комбінації є рівнобедрений трикутник, у який вписане коло. S R-радіус кулі, r-радіус конуса, H-висота конуса H R O 1 A O r B 4. Трикутник – це осьовий переріз конуса, SA=SB твірні конуса, АВ - діаметр основи конуса, коло велике коло вписаної кулі. Радіус кулі дорівнює радіусу кола вписаного в трикутник ASB. O
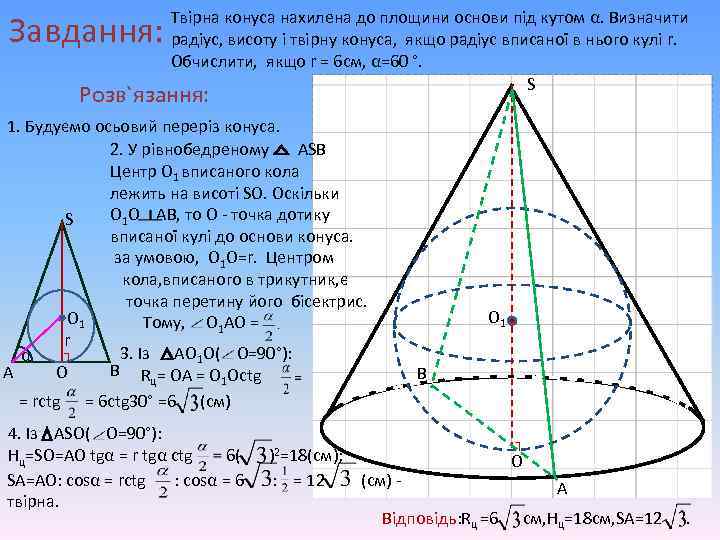
Завдання: Твірна конуса нахилена до площини основи під кутом α. Визначити радіус, висоту і твірну конуса, якщо радіус вписаної в нього кулі r. Обчислити, якщо r = 6 см, α=60 °. S Розв`язання: 1. Будуємо осьовий переріз конуса. 2. У рівнобедреному ASB Центр О 1 вписаного кола лежить на висоті SO. Оскільки О 1 О АВ, то О - точка дотику S вписаної кулі до основи конуса. за умовою, О 1 О=r. Центром кола, вписаного в трикутник, є точка перетину його бісектрис. О 1 Тому, О 1 АО = r ┐ 3. Із АО 1 О( О=90°): α B Rц= ОА = О 1 Оctg O A = rctg = 6 ctg 30° =6 (cм) 4. Із АSО( О=90°): Hц=SO=AO tgα = r tgα ctg 6( SA=AO: cosα = rctg : cosα = 6 твірна. О 1 B )2=18(cм); : = 12 (см) Відповідь: Rц =6 ┐ O A см, Hц=18 см, SA=12 .

Циліндр описаний навколо призми 1. Циліндр називається описаним навколо призми, якщо його основи - круги, описані навколо основ призми, а твірні збігаються з ребрами призми. 2. Вісь циліндра співпадає з висотою призми. 3. Радіус циліндра дорівнює радіусу кола описаного навколо основи призми. Завдання: У циліндр вписано правильну шестикутну призму. Знайдіть кут між діагоналлю її бічної грані і віссю циліндра, якщо радіус основи дорівнює висоті циліндра. R Hц R R Розв`язання: 1. Бічні грані призми - квадрати, оскільки сторона правильного шестикутника, вписаного у коло, дорівнює радіусу. 2. Бічні ребра призми паралельні осі циліндра, тому кут між діагоналлю грані і віссю циліндра дорівнює куту між діагоналлю і бічним ребром. Оскільки грані – квадрати, то цей кут дорівнює 45º. R Відповідь: 45°.

Циліндр вписаний в призму 1. Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра й перпендикулярна до площини осьового перерізу, що містить цю твірну. α ┴ β. 2. Циліндром, вписаним в призму, називається циліндр, основи якого круги, вписані в основи призми, а бічна поверхня циліндра дотикається бічних граней призми. Hц О 2 α 3. Вісь циліндра співпадає з висотою призми. 4. Радіус циліндра дорівнює радіусу кола вписаного в основу призми. β О 1 r

Піраміда вписана в конус 1. Конус називається описаним навколо піраміди, якщо його основа - круг, описаний навколо основи піраміди, вершина співпадає з вершиною піраміди, а твірні збігаються з ребрами піраміди. S 2. Висоти конуса і піраміди збігаються на основі єдиності прямої, перпендикулярної до площини і проведеної через точку, яка не лежить у даній площині. R - радіус конуса, який дорівнює радіусу описаного навколо основи піраміди кола. Завдання: Н Усі бічні ребра піраміди рівні Доведіть, що вона вписана у деякий конус. Розв`язання: 1. SO- перпендикуляр, опущений з вершини піраміди на площину основи; SA- довжина бічного ребра. 2. Вершини основи віддалені від точки О на одну й ту ж відстань О R А 3. Звідси випливає, що наша піраміда вписана в конус, вершина якого є вершиною піраміди, а основа - круг з центром О і радіусом R, що і потрібно було довести.
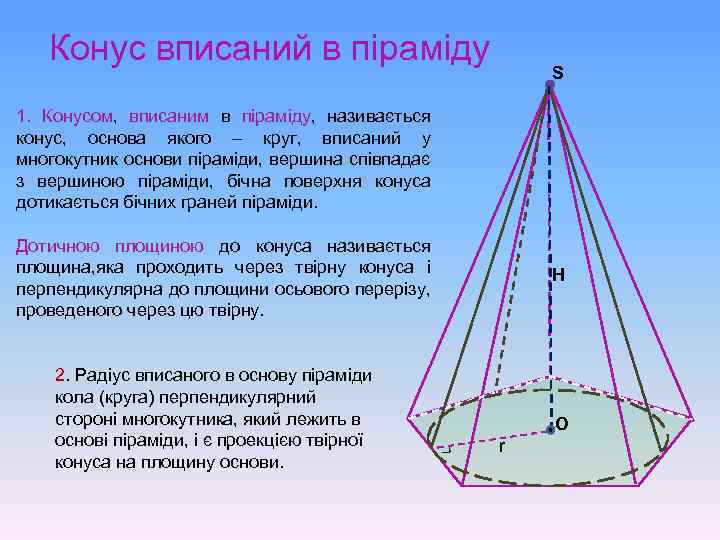
Конус вписаний в піраміду S 1. Конусом, вписаним в піраміду, називається конус, основа якого – круг, вписаний у многокутник основи піраміди, вершина співпадає з вершиною піраміди, бічна поверхня конуса дотикається бічних граней піраміди. Дотичною площиною до конуса називається площина, яка проходить через твірну конуса і перпендикулярна до площини осьового перерізу, проведеного через цю твірну. О ┐ 2. Радіус вписаного в основу піраміди кола (круга) перпендикулярний стороні многокутника, який лежить в основі піраміди, і є проекцією твірної конуса на площину основи. Н r
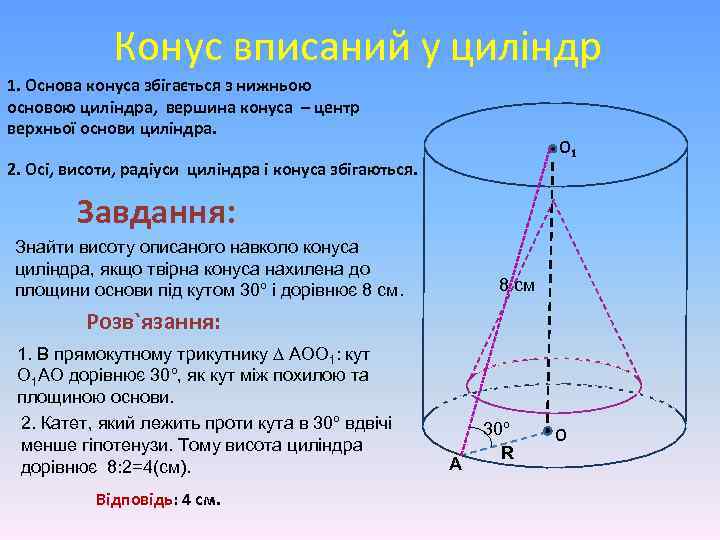
Конус вписаний у циліндр 1. Основа конуса збігається з нижньою основою циліндра, вершина конуса – центр верхньої основи циліндра. О 1 2. Осі, висоти, радіуси циліндра і конуса збігаються. Завдання: Знайти висоту описаного навколо конуса циліндра, якщо твірна конуса нахилена до площини основи під кутом 30º і дорівнює 8 см Розв`язання: 1. В прямокутному трикутнику ∆ АОО 1: кут О 1 АО дорівнює 30º, як кут між похилою та площиною основи. 2. Катет, який лежить проти кута в 30º вдвічі менше гіпотенузи. Тому висота циліндра дорівнює 8: 2=4(см). Відповідь: 4 см. А 30º R О
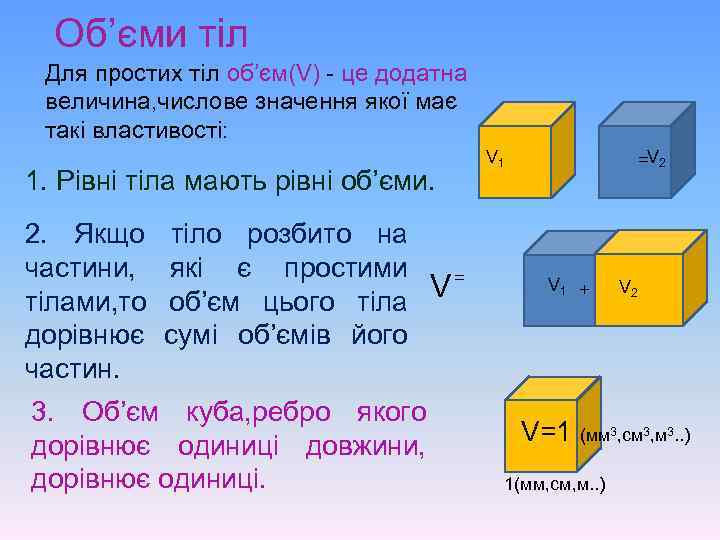
Об’єми тіл Для простих тіл об’єм(V) - це додатна величина, числове значення якої має такі властивості: 1. Рівні тіла мають рівні об’єми. 2. Якщо частини, тілами, то дорівнює частин. тіло розбито на які є простими = об’єм цього тіла V сумі об’ємів його 3. Об’єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці. V 1 =V 2 V 1 + V 2 V=1 (мм 3, см 3, м 3. . ) 1(мм, см, м. . )

Об’єм призми 1. Об’єм будь-якої призми дорівнює добутку площі основи та висоти. H Vпр=Sосн. H. Sосн 2. Для прямокутного паралелепіпеда V=abc, де a, b, c- його виміри. c b a 3. Для куба V=а 3, де а- довжина ребра. a 4. Для похилої призми об’єм можна обчислити як добуток площі перпендикулярного та довжини бічного ребра. V=Ql. l ┐ Q
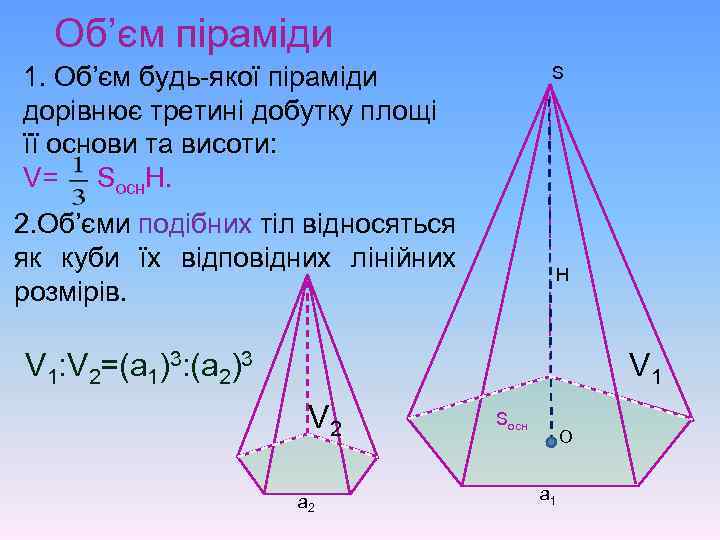
Об’єм піраміди 1. Об’єм будь-якої піраміди дорівнює третині добутку площі її основи та висоти: V= Sосн. H. S 2. Об’єми подібних тіл відносяться як куби їх відповідних лінійних розмірів. Н V 1: V 2=(a 1)3: (a 2)3 V 1 V 2 а 2 Sосн О а 1

Об’єми круглих тіл 1. Об’єм циліндра дорівнює добутку площі його основи та висоти. Vц= Sосн. H Н Sосн Vц= πR 2 H. 2. Об’єм конуса дорівнює одній третині добутку площі його основи та висоти. Vц= Sосн. H Vц= πR 2 H. Н 3. Об’єм кулі Vк= πR 3. R Vкульового сегмента =πH 2(R- ) Vкульового сектора = πR 2 H

Тестові завдання 1. Навколо кулі, радіусом 2 см, описано куб. Знайти об`єм куба. а) 8 см 3 б)16 см 3 г) 128 см 3 в) 64 см 3 2. Осьовим перерізом циліндра є прямокутник зі сторонами 6 см і 4 см. Більша сторона прямокутника є твірною циліндра. Знайти об`єм циліндра. б) 12πсм 3 в) 48πсм 3 г)12 см 3 а) 24πсм 3 3. Основою прямої призми є прямокутний трикутник з катетами 5 см і 8 см. Знайти об`єм призми, якщо її бічне ребро дорівнює 10 см. а) 400 см 3 в) 130 см 3 г) 390 см 3 б) 200 см 3 4. Прямокутний трикутник з катетами 3 см і 4 см обертається навколо більшого катета. Знайти об`єм тіла обертання. а) 48πсм 3 в) 36πсм 3 г) 15πсм 3 б) 12πсм 3 5. Основою піраміди є ромб зі стороною 5 см і висотою 4 см. Знайти об`єм піраміди, якщо її висота дорівнює 9 см. а) 90 см 3 б) 180 см 3 в) 54 см 3 г) 60 см 3

Тестові завдання 6. Об’єм кулі дорівнює а) 4 см б) 1 см πсм 3. Знайти її діаметр. г) см в) 2 см 7. Прямокутник із стороною а і діагоналлю d обертається навколо даної сторони. Визначити об`єм тіла обертання. б) π(d 2+a 2)a в) πa 2 d г) πa 2 см 3 а) π(d 2 -a 2)a 8. Осьовим перерізом конуса є рівносторонній трикутник зі стороною а Визначити об`єм конуса. а) в) г) б) 9. Сторона основи правильної трикутної призми а, а бічне ребро Визначити об`єм призми. а) в) г) б) 10. Основою піраміди є ромб з діагоналями d 1 і d 2. Знайти об`єм піраміди, якщо її висота дорівнює h. а) б) в) г) .

Література 1. Програма для загальноосвітніх навчальних закладів. Математика 5 -12 класи-К. Ірпінь, 2005. 2. Г. П. Бевз, В. П. Бевз, Математика 11 клас для загальноосвітніх закладів, рівень стандарт, Київ, ”Генеза”, 2011. 3. Г. В. Апостолова, Геометрія 11, підручник для загальноосвітніх закладів, академічний, профільний рівень, Київ, ”Генеза”, 2011. 4. М. Я. Забелишевська, Математика ЗНО 2009, Київ, ”Літера” ЛТД, 2009. -320 стр. 5. А. М. Чекова, Геометрія в таблицях. 7 -11 класи. Навч. посібник, Харків: Науково-методичний центр, 2003. -168 с. 6. Л. С. Сухарева, Геометрія. Завдання для усної роботи, математичні диктанти та тести, Харків, “Основа”, 2008.
4559_1.ppt