Количественные методы в финансах Процессы наращения и дисконтирования

Количественные методы в финансах Процессы наращения и дисконтирования. Процентная ставка. Москва-2008

Наращение Процесс наращения – это увеличение первоначальной суммы денег. Величина называется процентной ставкой за период наращения Т.

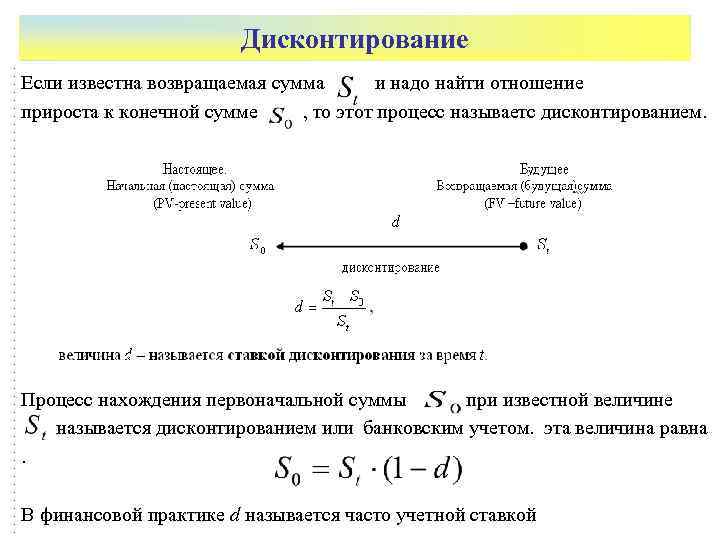Дисконтирование Если известна возвращаемая сумма и надо найти отношение прироста к конечной сумме , то этот процесс называетс дисконтированием. Процесс нахождения первоначальной суммы при известной величине называется дисконтированием или банковским учетом. эта величина равна. В финансовой практике d называется часто учетной ставкой

Процентная ставка Ø Существуют различные виды процентных ставок. Ставки наращения (interest base rate). Учетная ставка (discount rate) – используется в операциях банковского дисконтирования. Ø Процентные ставки бывают фиксированным и плавающими. Базовая процентная ставка показывает изменяющуюся во времени базу и размер надбавки к ней (маржу). Например, межбанковская ставка LIBOR (London interbank offered rate), базовая ставка по рублевым кредитам МИБОР. Ø Важные для финансовой деятельности процентные ставки имеют специальное название. Это ставки рефинансирования Центрального Банка России (для США Федеральной резервной системы). Ставка рефинансирования – это процентная ставка по которой ЦБ выдает кредиты коммерческим банкам. Ø Процентные ставки изменяются во времени, и зависимость от времени процентной ставки (временная структура процентной ставки)

Величина процентной ставки Время – важнейший фактор в финансовых операциях. Деньги, относящиеся к разным моментам времени неравноценны. Ø Процентная ставка учитывает фактор времени. В контрактах обязательно указывается сроки, периоды выплаты денег. Фраза «доллар сегодня дороже, чем доллар завтра» , отражает основной принцип неравноценности денег, относящихся к разным моментам времени (time-value of many). Имеющуюся сегодня сумму можно инвестировать и получить в будущем доход, и сегодняшние 1000 руб. имеют большую ценность чем те же 1000 руб. через три или пять лет с учетом инфляции и рисков невозврата инвестиции (кредита). Фактор времени в долгосрочных операциях иногда оказывается важнее, чем величина суммы денег. Ø Процентная ставка учитывает временной интервал, который называется периодом начисления (running period). Периодом начисления может быть год, квартал, месяц, день. В практической деятельности и в статистике обычно подразумеваются годовые процентные ставки. Ø Процентная ставка учитывает риски финансовых операций и инфляцию. Ø Процентная ставка является мерой эффективности (доходности) финансовой деятельности, кредитования, инвестиции, коммерческой деятельности.

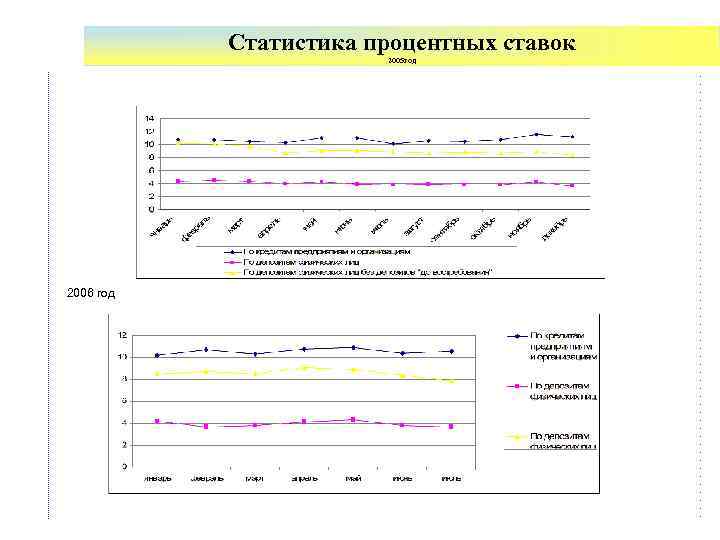Статистика процентных ставок 2005 год 2006 год

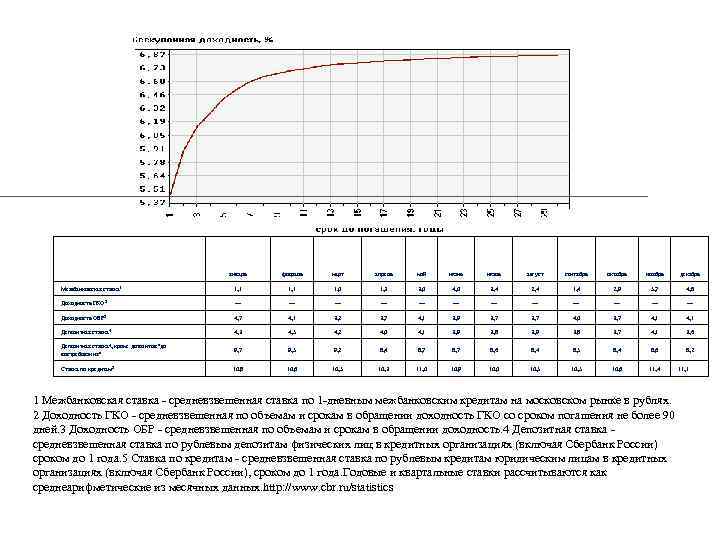январь Межбанковская ставка 1 февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь 1, 1 1, 0 1, 3 3, 0 4, 0 3, 4 2, 4 1, 4 2, 9 5, 7 4, 8 Доходность ГКО 2 — — — Доходность ОБР 3 4, 7 4, 1 3, 2 3, 7 4, 1 3, 9 3, 7 4, 0 3, 7 4, 1 Депозитная ставка 4 4, 3 4, 5 4, 2 4, 0 4, 1 3, 9 3, 8 3, 7 4, 1 3, 6 9, 7 9, 5 9, 2 8, 4 8, 7 8, 6 8, 4 8, 5 8, 4 8, 6 8, 2 10, 8 10, 6 10, 5 10, 3 11, 0 10, 9 10, 0 10, 5 10, 6 11, 4 Депозитная ставка 4, кроме депозитов "до востребования" Ставка по кредитам 5 11, 1 1 Межбанковская ставка - средневзвешенная ставка по 1 -дневным межбанковским кредитам на московском рынке в рублях. 2 Доходность ГКО - средневзвешенная по объемам и срокам в обращении доходность ГКО со сроком погашения не более 90 дней. 3 Доходность ОБР - средневзвешенная по объемам и срокам в обращении доходность. 4 Депозитная ставка - средневзвешенная ставка по рублевым депозитам физических лиц в кредитных организациях (включая Сбербанк России) сроком до 1 года. 5 Ставка по кредитам - средневзвешенная ставка по рублевым кредитам юридическим лицам в кредитных организациях (включая Сбербанк России), сроком до 1 года. Годовые и квартальные ставки рассчитываются как среднеарифметические из месячных данных. http: //www. cbr. ru/statistics

Простой процент начисляется за все время действия контракта на определенную первоначальную сумму. Этот способ начисления процентов называют “наращиванием без капитализации”. Наращенная сумма при ежегодном начислении процентов или будущая стоимость ( future value) равна где r – годовая процентная ставка n – число лет. При ежедневном начислении простых процентов наращенная сумма равна где - временная база, или число дней в финансовом году, Т – число дней наращения. Процентный доход равен ( ) или ( ).

Простой процент Если простые процентные ставки меняются в течении некоторого периода, то сумма на счете равна где , ……. процентные ставки за соотвествующие периоды. Накопленный процентный доход равен Если имеется последовательность простых процентных ставок за последовательные периоды , то согласно принципу эквивалентности процентных ставок средневзвешенная процентная ставка равна

Пример 1. Фирма получила кредит на один год в размере 10 млн. руб. с условием возврата: а) 15 млн. руб. , б) 10, 5 млн. руб. Найти процентную ставку и дисконт.

Пример 2. Кредит был выдан под 12% годовых. Найти начальную сумму, если возвращаемая сумма равна 650 тыс. руб. Решение. Расчет начальной суммы можно произвести двумя способами. По методу банковского дисконтирования начальная сумма равна = 572000. руб. процентные платежи равны Начальная сумма, рассчитанная по методу математического дисконтирования, равна 580357, 14 руб. Процентные платежи равны = 69642, 86 руб

Пример 5. Банк предлагает депозит с начислением на первоначальную сумму. Первые три месяца по ставке 4% годовых, в следующие три месяца процентная ставка увеличивается на 0, 5%. Найти наращенную сумму и процентный доход, если сумма вклада составляет 30 000 руб. Процентный доход за первые три месяца равен Процентный доход за следующие три месяца равен За все шесть месяцев процентный доход равен 300+337, 5=637, 5 руб Наращенная сумма равна 30637, 5 руб

Сложный процент Начисление сложного процента осуществляется на наращенную сумму, поэтому этот способ начисления называют «наращением с капитализацией» . Наращенная сумма при начислении сложного процента за произвольное число дней равна где r- годовая процентная ставка (per annual), выраженная в виде долей единицы. Если начисление сложных процентов происходит m раз в году течении n лет, то расчет наращенной суммы за время производят по формуле где r – годовая процентная ставка (номинальная ), – процентная ставка за период. Величина – называется множителем наращения, а коэффициентом наращения. Наращенная сумма зависит от частоты начисления процентов. Чем больше частота начисления процентов, тем больше наращенная сумма.

Сложный процент называется множителем наращения коэффициентом наращения В кредитных контрактах и депозитных договорах, когда начисление процентов происходит по сложной процентной ставке, указывается годовая процентная ставка, которая называется номинальной

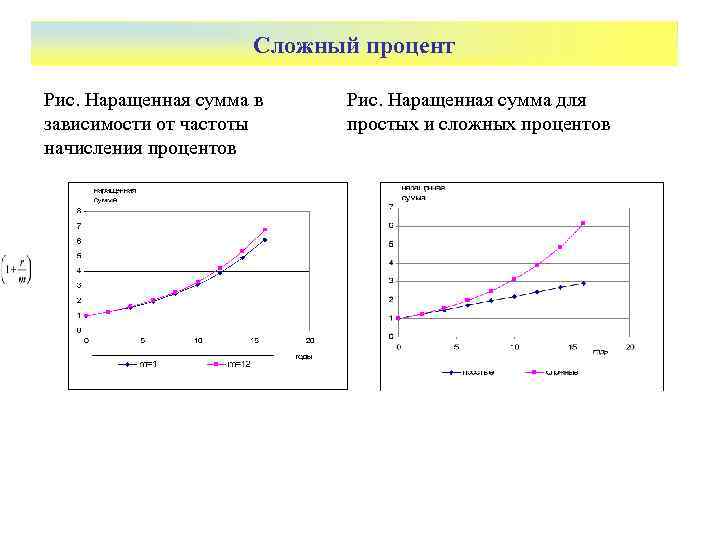Сложный процент Рис. Наращенная сумма в зависимости от частоты начисления процентов Рис. Наращенная сумма для простых и сложных процентов

Непрерывное начисление процентов Если частота начисления процентов становится непрерывной, то есть частота начисления процентов бесконечно возрастает , а временной интервал начисления становится бесконечно малым, то наращенная сумма или будущая стоимость рассчитывается по формуле При непрерывном начислении процентов наращенная сумма рассчитывается по формуле где сила роста, которая является фактически непрерывной процентной ставкой. Если сила роста постоянна, то наращенная сумма за время t равна

, Полезные формулы При нестабильной экономике процентные ставки могут значительно изменяться в течение года. В этом случае наращенная сумма вычисляется по формуле , Если необходимо найти количество лет для увеличения начальной суммы в N раз, то для простых процентов получим для сложных процентов

Примеры Пример 6. Сколько лет потребуется для увеличения первоначальной суммы в 1, 2 раза, если номинальная процентная ставка равна 9%, а начисление процентов происходит 4 раза в год. Решение. Найдем необходимое число лет: N = 1, 2; m = 4. ≈ 2 года

Пример Какую сумму можно разместить на депозите, чтобы через три года получить 4 млн. руб. при ставке сложных процентов а) 8% годовых б) 12% годовых. Рассмотреть случаи, когда начисление процентов происходит раз в год, два раза в год. Решение. В этой задаче надо найти начальную сумму. Для этого из формулы для наращения сложных процентов надо найти. .

Пример Фирма получила в кредит на 3 года сумму равную 50 млн. руб. с условием возврата 55 млн. руб. Найти процентные ставки по этому кредиту, если проценты начисляются: а) по простой процентной ставке; б) по сложной процентной ставке при начислении процентов раз в квартал; в) по сложной процентной ставке при начисления процентов ежемесячно. Решение. Из формулы наращенной суммы для простых процентов найдем выражение для простой процентной ставки. Из формулы для номинальной (сложной) процентной ставки найдем выражение для сложной процентной ставки.

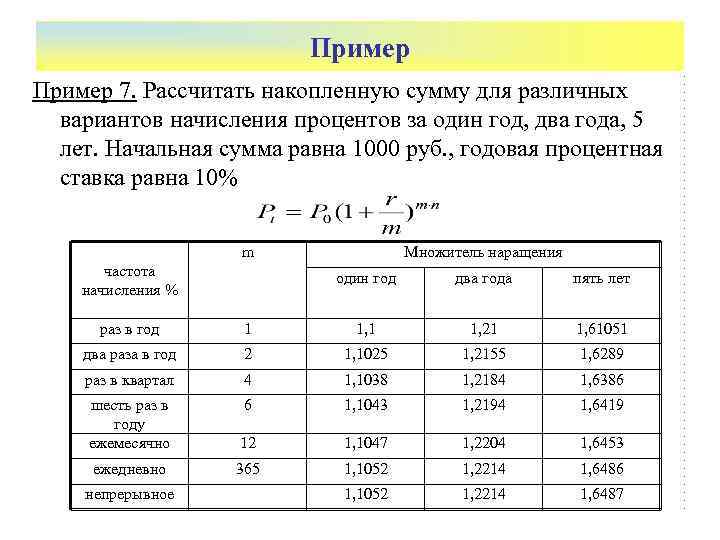Пример 7. Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, два года, 5 лет. Начальная сумма равна 1000 руб. , годовая процентная ставка равна 10% m частота начисления % Множитель наращения один год два года пять лет раз в год 1 1, 21 1, 61051 два раза в год 2 1, 1025 1, 2155 1, 6289 раз в квартал 4 1, 1038 1, 2184 1, 6386 шесть раз в году ежемесячно 6 1, 1043 1, 2194 1, 6419 12 1, 1047 1, 2204 1, 6453 ежедневно 365 1, 1052 1, 2214 1, 6486 1, 1052 1, 2214 1, 6487 непрерывное

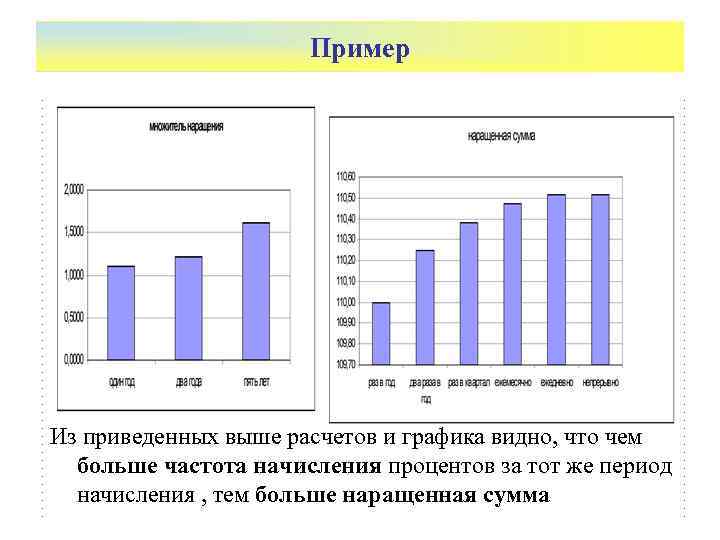Пример Из приведенных выше расчетов и графика видно, что чем больше частота начисления процентов за тот же период начисления , тем больше наращенная сумма

Процентная ставка в условиях инфляции. Процентная ставка, учитывающая инфляцию, называется номинальной и равна где r – номинальная процентная ставка, – реальная процентная ставка, темп инфляции Пример. Кредит 12, 0 млн. руб. был выдан на 3 года. На этот период прогнозируется рост цен в 2, 2 раза. Определить ставку процента при выдаче кредита и наращенную сумму долга, если реальная доходность этой финансовой операции для кредитора должна составлять 12% годовых. Решение. Годовой рост цен равен. Индекс цен за год равен , Темп инфляции найдем из формулы Реальная процентная ставка 0, 12. Номинальная процентная ставка по формуле равна Наращенная сумма долга равна млн. руб.

Эффективная процентная ставка Эффективной процентной ставкой называется годичная ставка сложных процентов, дающая тот же финансовый результат: соотношение между полученной суммой за время t = T и затраченной суммой , которая получается при любой схеме выплат где Т измеряется в годах. Если проценты начисляются m раз в год по схеме сложных процентов, то формула (1. 20) приобретает более простой вид Эффективная процентная ставка позволяет сравнить доходности различных финансовых операций или, другими словами, сравнить различные методы получения процентного дохода.

Пример Банк начисляет по счету 10% годовых. Капитализация процентов осуществляется ежеквартально. Определить величину эффективного процента. Эффективная процентная ставка – это годовая процентная ставка сложных процентов с начислением раз в году. Из формулы. Подставляя данные задачи получим =0, 1038

Эффективная процентная ставка Пример. Предприниматель может получить ссуду: а) на условиях ежеквартального начисления сложных процентов из расчета 75% годовых, б) на условиях полугодового начисления сложных процентов из расчета 80% годовых. Какой вариант предпочесть? Задачу можно решить двумя способами: 1) сравнить наращенные суммы, 2) сравнить эффективные процентные ставки. Решение. Наращенная сумма при ежеквартальном начислении сложных процентов равна руб. Наращенная сумма при полугодовом начислении сложных процентов равна m = 2; 196000 руб Найдем эффективную процентную ставку для варианта а): m = 4; r = 0, 75; 0, 9885 (98, 85%); для варианта б) m = 2; r = 0, 80; 0, 96 (96, 0%).

Математическое дисконтирование Часто при выдаче кредита необходимо найти первоначальную сумму при известной конечной сумме. В зависимости от вида процентной ставки используют два типа дисконтирования. Дисконтирование по процентной ставке r называется математическое дисконтированием, а дисконтирование по учетной ставке d называется банковским дисконтированием. Математическое дисконтирование. для простых процентов для сложных процентов с начислением процентов m раз в году, для непрерывных процентов

Банковское дисконтирование При банковском дисконтировании, так же как и при математическом дисконтировании, требуется найти начальную сумму, выданную в кредит при известной сумме погашения кредита через период t. Процентный доход за кредит выплачивается сразу при выдаче суммы кредита, которая меньше на величину наращенных процентов, рассчитанных по учетной ставке d По простой учетной ставке По сложной учетной ставке Если дисконтирование проводится m раз в год, то дисконтированная сумма равна При непрерывном дисконтировании

Декурсивный и антисипативный методы наращения Для операций наращения важным является также момент начисления процентов. Начисление процентов может в начале периода начисления или в конце периода начисления. Декурсивный (последующий) метод – начисление процентов происходит в конце расчетного периода. При этом наращенная сумма рассчитывается, как правило по процентной ставке r. Антисипативный (предварительный) метод – начисление процентов происходит в начале расчетного периода на сумму, которую следует вернуть, наращенная сумма рассчитывается, как правило, по учетной ставке d. Пример. Срочный вклад в размере 800 тыс. руб. положен в банк на 2, 5 года. На вклад начисляются сложные проценты по учетной ставке d = 15% годовых. Рассчитать наращенную сумму по двум методам а) декурсивному , б) антисипативном. Наращенная сумма по декурсивному методу равна Наращенная сумма по антисипативному методу равна

Эквивалентность процентных ставок Процентные и учетные ставки в кредитных операциях решают одну и ту же задачу: определяют величину наращенной или дисконтированной суммы. Процентные ставки, обеспечивающие равноценность финансовых результатов, называются эквивалентными или релятивными (относительными). Эквивалентные процентные ставки означают, что безразлично, по какой процентной ставке получается данная конечная сумма. Соотношения эквивалентности для процентных ставок легко получается из условия равенства отношения наращенной суммы к начальной сумме, т. е. равенства дисконтных множителей или множителей наращения. Ø Соотношения эквивалентности простой процентной ставки и учетной ставки Ø Соотношения эквивалентности простой и сложной номинальной ставок

Эквивалентность процентных ставок. Пример. Ссуда выдана на 1, 5 года под 25% простых годовых процентов. Найти эквивалентную ставку сложных процентов при начислении процентов раз (два) в год. Решение. Из соотношения эквивалентности получим для m =1 для m = 2 0, 22398 Пример. Какой годовой ставке простых процентов соответствует годовая ставка сложных процентов 20%, если начисление по ней производится ежеквартально в течении 2 лет. Решение.

Эквивалентность процентных ставок. Эквивалентность простой учетной и номинальной сложной процентной ставок для эквивалентной номинальной сложной ставки для эквивалентной учетной ставки Пример. Банк выдал ссуду на 1 год и 3 мес. Под 20% годовых сложных процентов с ежемесячным начислением. Найти величину простой учетной ставки, при которой банк получил такую же наращенную сумму. Решение. При m = 4, r = 0, 2 эквивалентная простая учетная ставка равна

Пример Вкладчик размещает на счете 2 000 руб. на три года. Банк начисляет простой процент. Процентная ставка за первый год равна 8%, второй – 9%, третий – 10%. Определить, какая сумма будет получена по счету через 3 года?

Пример Инвестор открывает в банке депозит на 90 дней под 10% годовых и хотел бы в конце периода получить по депозиту 10 тыс. руб. Какую сумму ему следует разместить сегодня на счете? База 365 дней. Решение. Для решения используем формулу

Пример Вкладчик разместил на счете в банке 10 000 руб. и получил через 180 дней 10 540 руб. По счету начислялся простой процент. Определить доходность его операции в расчете на год на основе простого процента. Финансовый год равен 365 дням. (10, 95% годовых) Вкладчик размещает в банке 2 000 руб. под 8% годовых. Банк осуществляет капитализацию процентов на счете ежеквартально. Какая сумма денег получится на счете через 3 года? . Решение. Расчет проведем по формуле = 2536, 48

Пример Вкладчик размещает в банке 1 000 руб. на три года. Капитализация процентов осуществляется ежегодно. За первый год банк начисляет 10%, второй – 9%, третий – 8% годовых. Какая сумма денег получится на счете через 3 года Решение. = 1270.

Пример В начале года вкладчик размещает в банке 2 000 руб. под 8% годовых. Банк осуществляет капитализацию процентов в конце каждого года. В течение года по счету начисляется простой процент. Какая сумма денег получится на счете через 3 года и 90 дней? База 365 дней Решение. = 2569, 12

Пример В начале года инвестор открывает в банке депозит на сумму 1 млн. руб. и хотел бы получить по счету 1 092 025 руб. Банк начисляет 9% годовых, капитализация процентов осуществляется через каждые полгода. На какой период времени следует открыть депозит? Из формулы найдем n= подставляя данные задачи получим n=1 год.

Пример Банк А выплачивает сложные проценты раз в полгода. Банк Б выплачивает 12% годовых по простой процентной ставке. Вкладчик разместил по 10 000 руб. в банках А и Б сроком на 2 года. Какую полугодовую процентную ставку должен начислять банк А, чтобы у вкладчика по итогам 2 -х лет суммы в банках были одинаковы? Для решения этой задачи необходимо приравнять множители наращения, т. е Подставляя данные задачи, получим Выполняя преобразования, получим 0, 553

Вексель номиналом в 50 000 и сроком на 90 дней был учтен через 60. . Учетная ставка равна 12%. Найти величину дисконта при учете векселя. Для вычисления дисконта за учет векселя надо воспользоваться формулой для учета векселя

Доходность Простая доходность за k месяцев Валовый доход за k месяцев Пусть в момент t стоимость акции была 80, через месяц он стала стоить 85. Простая доходность равна

Простая доходность Доходность за два месяца равна

Простая доходность Пусть цена акции еще через месяц стала 90 Доходность за два месяца равна Или Т. е. валовая доходность или совокупный процентный доход есть геометрическое среднее

Простая доходность за k периодов равна среднегеометрическому доходностей за периоды Или Если доходность акции за каждый месяц 0, 0588, то за 12 месяцев получим

Непрерывная доходность Цены финансовых активов могут меняться непрерывно Доходность за период t=1 равна За k периодов - - это непрерывно накапливаемый доход величина непрерывно накапливаемых доходов за промежуток времени больший, чем 1 день равна сумме однодневных доходов

Непрервывная доходность и простая доходность Стоимость акции

Ключевые слова Наращение. Дисконтирование. Простой процент. Сложный процент. Период начисления (дисконтирования). Частота начисления процента. Сила роста (непрерывный процент ). Учетная ставка. Банковский учет (коммерческое дисконтирование). Математическое дисконтирование. Эффективная процентная ставка. Номинальная процентная ставка. Реальная процентная ставка и темп инфляции. Эквивалентность процентных ставок. Доходность финансовой операции.

Литература Основная. 1. Е. М. Четыркин. Финансовая математика. Учебник. М. Изд -во «Дело» , 2006. гл. 1 -3, стр. 11 – 65.