Колебательные процессы. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы апериодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы. • Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы Предположим что вынуждающая сила изменяется со временем по гармоническому закону •
Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. Возвращающая сила x - смещение маятника от положения равновесия. Второй закон Ньютона в нашем случае запишется так:
Это уравнение и есть дифференциальное уравнение вынужденных колебаний пружинного маятника. Его принято записывать в следующем, так называемом каноническом виде: w 0 - коэффициент затухания, - собственная частота свободных колебаний пружинного маятника.
Решение этого уравнения будет представляться в виде суммы общего решения однородного уравнения и частного решения неоднородного уравнения. Решение однородного уравнения, включает в себя три возможных сценария (режим апериодического затухания, граничный режим и колебательное решение в случае малого затухания). Определим частное решение неоднородного уравнения. Здесь удобнее перейти к комплексной форме дифференциального уравнения, которое запишется как
Будем искать частное решение в виде то есть предположим, что колебания в системе будут происходить с частотой внешней силы ω и, возможно, с некоторым сдвигом φ. В результате имеем Подставляя это в дифференциальное уравнение, получаем
По формуле Лапласа Поэтому можно записать: Приравнивая отдельно действительную и мнимую части, получаем Из этой системы уравнений мы определим коэффициент B и угол φ. Возводя обе части в квадрат и складывая, находим: гол φ найдем, разделив второе уравнение на первое: Итак, частное решение неоднородного уравнения в комплексной форме имеет вид где угол сдвига φ вычисляется по полученной выше формуле. Соответственно, действительная часть решения записывается как
Окончательный ответ представляет собой сумму двух членов: где xодн(t) − общее решение однородного уравнения, описывающего осциллятор с затуханием без действия вынужденной силы. Заметим, что вследствие затухания решение однородного уравнения xодн(t) будет стремиться к нулю. Поэтому в установившемся режиме характер колебаний будет зависеть лишь от вынужденной силы, то есть будет определяться вторым компонентом общего решения: где , β − коэффициент затухания. Эта формула описывает также и явление резонанса, причем максимальная амплитуда установившихся колебаний при резонансе будет конечной и равной Зависимость амплитуды установившихся колебаний xmax от частоты вынужденной силы ω вблизи резонананса при различных коэффициентах затухания β показана ниже на рисунке. Такие кривые называются резонансными кривыми.
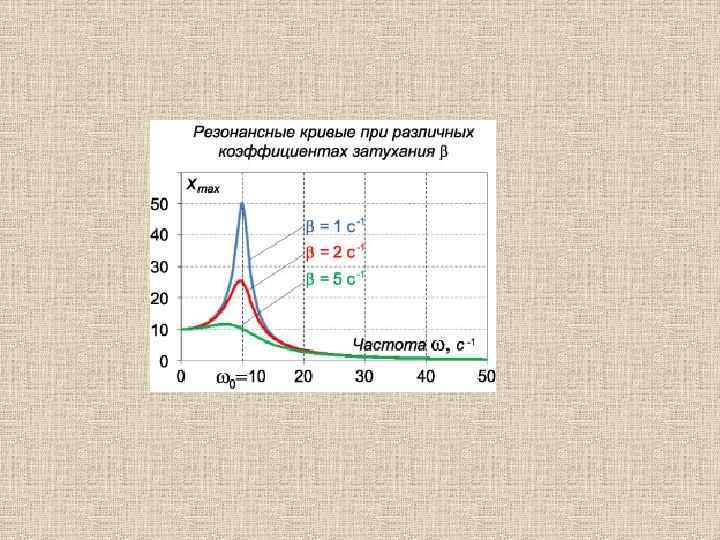
• Для оценки свойств колебательной системы в окрестности резонанса используют понятие добротности. Добротность показывает во сколько раз амплитуда вынужденных колебаний при резонансе превышает их амплитуду вдали от резонанса. • При стремлении частоты вынужденной силы ω к нулю амплитуда колебаний механической системы приближается к : Поэтому добротность механической колебательной системы будет равна где β − коэффициент затухания. Добротность является очень полезной характеристикой. С энергетической точки зрения она показывает отношение энергии, запасенной в колебательной системе, к энергии, которую система теряет за один период колебаний. Потери энергии характеризуются также логарифмическим декрементом затухания δ. Соотношение между добротностью Q и логарифмическим декрементом затухания δ (при малых δ) выражается простой формулой:
ЭНЕРГИЯ, ПЕРЕДАВАЕМАЯ КОЛЕБЛЮЩЕЙСЯ СИСТЕМЕ ВНЕШНЕЙ СИЛОЙ. Внешняя периодическая сила подводит к системе энергию. ВОПРОС: на что расходуется эта энергия? Вся энергия источника колебаний расходуется на преодоление сил трения системы. Рассмотрим мощность (энергия в единицу времени) наших колебаний, которая по определению равна
Скачать презентацию Колебательные процессы ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В случае вынужденных
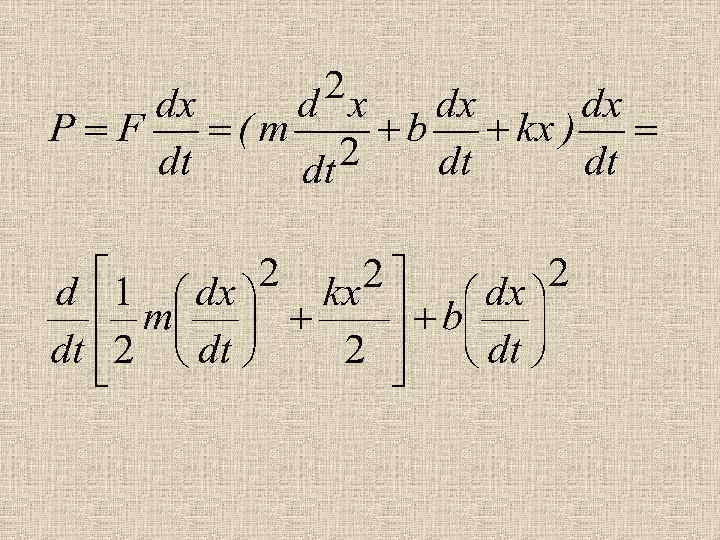
VYNUZhDENNYE_KOLEBANIYa_L3_2014.pptx