КОЛЕБАНИЯ Колебания это процессы повторяющиеся во времени

КОЛЕБАНИЯ Колебания – это процессы, повторяющиеся во времени. По природе могут быть: • механическими; • электромагнитными; • тепловыми и др.

1. Механические гармонические колебания К колебаниям относят движения или процессы, в той или иной степени повторяющиеся с течением времени. Колебания, происходящие по закону косинуса или синуса, называются гармоническими. Уравнение гармонических колебаний: или , где x — колеблющаяся величина, x 0 — амплитуда колебаний; w — круговая (циклическая) частота; t — время; --начальная фаза. — фаза колебаний;

Период колебаний T — время, за которое совершается одно полное колебание, где N — число полных колебаний, совершаемых за вре Частота колебаний. — число колебаний, совершаемых за 1 с, , или Круговая (циклическая) частота колебаний

Скорость точки, совершающей гармонические колебания, равна производной по времени от ее координаты x, а ускорение точки — второй производной. . Если ускорение , то

Возвращающая сила , где m — масса точки. Полная механическая энергия колеблющейся точки , где — соответственно и кинетическая и потенциальная энергии.

Период колебаний математического маятника , где l — длина маятника, g — ускорение свободного падения. Период колебаний пружинного маятника , где m — масса груза, подвешенного на пружине; k — коэффициент

2. Электромагнитные Переменный ток колебания. . Период свободных электромагнитных колебаний в колебательном контуре, состоящем из емкости C и индуктивности L, определяется по формуле Томпсона:

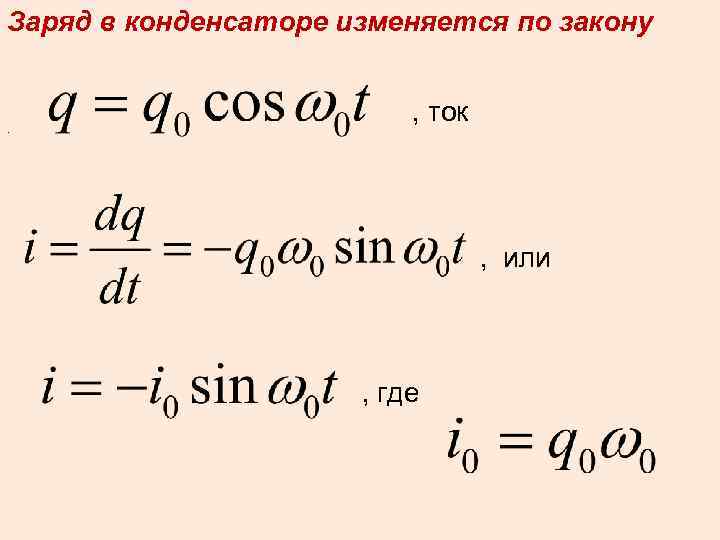
Заряд в конденсаторе изменяется по закону . , ток , или , где

Энергия электрического поля конденсатора магнитного поля катушки Полная энергия сохраняется

Мгновенные значения силы тока i и напряжения , u в цепи переменного тока соответственно равны , где I 0 и Uo — амплитудные значения силы тока и напряжения. Сдвиг фаз j между током и напряжением определяется формулой где L — индуктивность; C — емкость; R — активное сопротивление, последовательно включенное в цепь переменного тока.

Значение постоянного тока, который в цепи с активным сопротивлением выделяет такую же мощность, что и переменный ток с данным амплитудным значением, называется . действующим значением переменного тока (так же определяется и действующее значение напряжения). Мощность переменного тока на участке цепи

IV. Решение расчетных и качественных задач. Если в задаче по теме «Колебания и волны» задано уравнение гармонических колебаний, то величины, характеризующие колебания, могут быть найдены путем сопоставления данного уравнения с общим уравнением гармонических колебаний. Уравнение гармонических колебаний может быть записано как по закону синуса, так и по закону косинуса в зависимости от задания начальной фазы колебаний. В задачах о математическом маятнике, точка подвеса которого движется с ускорением , необходимо учитывать проявление сил инерции в создании эффективного поля гравитации и период колебаний такого маятника находится по формуле

В задачах об электромагнитных колебаниях используется формула Томсона, а также зависимость между длиной волны l, скоростью распространения колебаний v и периодом T: l = v. T. В задачах о переменном токе нужно установить наличие в схеме активного, емкостного и индуктивного сопротивлений, применить закон Ома для переменного тока. Количество теплоты, выделяемое при прохождении переменного тока по проводнику с активным сопротивлением R, определяется по формуле Q = I 2 Rt, где t — время прохождения тока; I — действующее значение тока.

V Домашнее задание. Г. П. Киселева ФИЗИКА 2005 г. Теория стр. 69 -72 Задачи Тест 14. 1

Физическую систему, совершающую колебания, называют осциллятором. Классический осциллятор — механическая система, совершающая колебания около положения устойчивого равновесия (маятник).

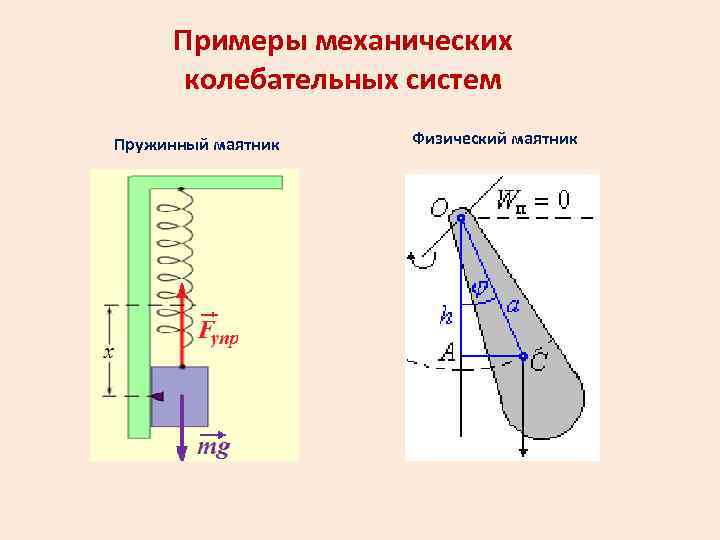
Примеры механических колебательных систем Пружинный маятник Физический маятник