КОГДА МОДУЛЬ МОЖНО НЕ РАСКРЫВАТЬ Свойства модуля Свойство

КОГДА МОДУЛЬ МОЖНО НЕ РАСКРЫВАТЬ. Свойства модуля: Свойство 1. Для любого действительного a Свойство 2. Свойство 3. (для неравенств) Свойство 4. Свойство 5. Для любых действительных a и b Свойство 6. Свойство 7.

Решить уравнение а) применим метод «промежутков» Ответ:

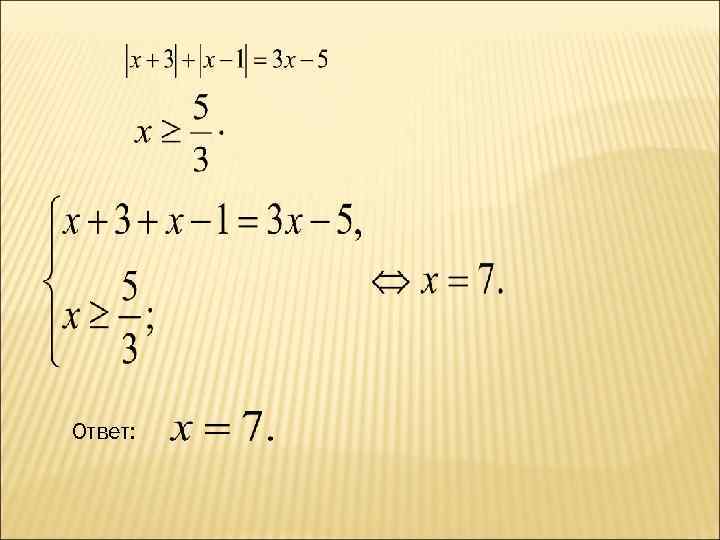Ответ:

Для самостоятельного решения Ответ: нет решений.

ПРИМЕНЕНИЕ 2 СВОЙСТВА

Решить уравнение Пусть Поскольку то, применяя свойство 2 можно сразу перейти к системе, равносильной данному уравнению Ответ:

Для самостоятельного решения Ответ :

РЕШИТЬ СИСТЕМУ Перепишем систему в виде: Тогда Ее решение - это все точки отрезка AB прямой x+y=9.

Для самостоятельного решения Ответ : все точки отрезка AB прямой x+y=7, где A(1; 6), B(5; 2).

РЕШИТЬ СИСТЕМУ Сложим (1) и (2): По свойству 2 Отсюда Ответ:

ПРИМЕНЕНИЕ СВОЙСТВА 3

Решить уравнение Преобразуем правую часть уравнения, не изменяя область определения последнего. Имеем Тогда исходное уравнение становится таким: В силу свойства 3 Ответ:

Для самостоятельного решения Ответ :

РЕШИТЬ УРАВНЕНИЕ: Применим свойство 3 Тогда Ответ:

РЕШИТЬ НЕРАВЕНСТВО Применим свойство 3. (для неравенств) Тогда Ответ:

ПРИМЕНЕНИЕ СВОЙСТВА 4

2 способ решения уравнения Т. к. Применим свойство 4 то Ответ:

Разновидность свойства 4 уравнение равносильно неравенству Геометрическая интерпретация. Это уравнение говорит о том, что сумма расстояний на координатной прямой от точки с координатой x до точек с координатами a и b равна b-a.

ПРИ КАКИХ УРАВНЕНИЕ ИМЕЕТ НЕ МЕНЕЕ 4 РАЗЛИЧНЫХ РЕШЕНИЙ , ЯВЛЯЮЩИХСЯ ЦЕЛЫМИ ЧИСЛАМИ? Т. к. левая часть уравнения неотрицательна, то По свойству 4 имеем: Тогда уравнение равносильно неравенству Отрезок Получаем условие Ответ: должен содержать 4 различных целых числа.

Для самостоятельного решения При каких действительных a уравнение имеет не менее четырех решений, являющихся целыми числами? Ответ:

ПРИМЕНЕНИЕ СВОЙСТВА 5

РЕШИТЬ СИСТЕМУ Перепишем систему: По свойству 5 для любых действительных a и b Т. е. Ответ: решений нет.

Для самостоятельного решения Ответ: нет решений.

РЕШИТЬ НЕРАВЕНСТВО Т. к. то равносильно преобразуем правую часть

Неравенство равносильно По свойству 5 для любых действительных a и b это неравенство верно при всех допустимых x, его решением будет область определения неравенства. Ответ:

ПРИМЕНЕНИЕ СВОЙСТВА 6

РЕШИТЬ НЕРАВЕНСТВО Применим свойство 6 тогда исходное неравенство равносильно Ответ:

Решить уравнение Заметив, что , а уравнения можно преобразовать так: , левую часть данного Таким образом, исходное уравнение равносильно уравнению , а это, в свою очередь, такомут. е. Ответ:

ПРИМЕНЕНИЕ СВОЙСТВА 7

РЕШИМ СИСТЕМУ Ответ: 2 луча

Спасибо за внимание