Кодирование различных видов информации ТЕСТИРОВАНИЕ САЙТ www.

Кодирование различных видов информации

ТЕСТИРОВАНИЕ САЙТ www. i-exam. ru Ключ доступа для самотестирования 186372 tt 819 2

Кодирование текстовой информации 1 символ = 1 байт (8 бит) В персональных компьютерах и телекоммуникационных системах принят международный стандарт кодирования ASCII (American Standard Code for Information Interchange) Он охватывает первую часть кодовой таблицы (коды от 0 до 127, первый бит 0). Это латинский алфавит, цифры, знаки, специальные символы и др. Вторая часть кодовой таблицы (коды от 128 до 255) используется для национальных алфавитов и имеет свои стандарты. Например, КОИ-8 или ISO для кириллицы В настоящее время все чаще используется стандарт Unicode: 1 символ = 2 байта (16 бит) Это позволяет закодировать 216 = 65536 различных символов и использовать единую кодовую таблицу для большинства популярных алфавитов Знак Код пробел 00100000 A 01000001 Z 01011010 0 00110000 9 00111001 [Esc] 00011011 [Enter] 00001101

Пример. Книга содержит 100 страниц. На каждой странице - 35 строк, в каждой строке - 50 символов. Рассчитать объем информации, содержащийся в книге, если при кодировании были использованы ASCII коды. Решение. 1. Страница содержит 35 x 50 = 1750 байт информации. Объем всей информации в книге (в разных единицах): 1. 1750 x 100 = 175000 байт. 2. 175000 / 1024 = 170, 8984 Кбайт. 3. 170, 8984 / 1024 = 0, 166893 Мбайт.

Кодирование числовой информации. Компьютерная арифметика Для хранения числа отводится ограниченная память, поэтому диапазон чисел конечен. Выход за пределы этого диапазона вызывает сообщения об ошибке. Целые и вещественные числа представляются и обрабатываются в компьютере по-разному. Для хранения целого числа отводится 4 байта памяти, для хранения вещественных до 8 байт. Сложение неотрицательных целых чисел выполняется по правилам двоичной арифметики. Вычитание выполняется как сложение с отрицательным числом с отбрасыванием старшего разряда.

Представление вещественных чисел Вещественное число представляется в нормализованной форме: X = ± M * 10±k M называется мантиссой, 0, 1≤M<1, k называется порядком. В памяти компьютера мантисса и порядок хранятся как два целых двоичных числа. На мантиссу обычно отводится 4 байта , на порядок – 2 байта, т. е. 6 байтов на число Вещественные вычисления всегда производятся с округлением. Вычисления с вещественными числами выполняются по сложным алгоритмам, поэтому требуют больше времени, чем целочисленные. Число Нормализ. форма Мантисса Порядок 123, 45 0, 12345*103 0, 12345 3 -12000 -0, 12*105 -0, 12 5 0, 00015 0, 15*10 -3 0, 15 -3

Система счисления - ЭТО ЗНАКОВАЯ СИСТЕМА, В КОТОРОЙ ЧИСЛА ЗАПИСЫВАЮТСЯ ПО ОПРЕДЕЛЕННЫМ ПРАВИЛАМ С ПОМОЩЬЮ СИМВОЛОВ НЕКОТОРОГО АЛФАВИТА. • позиционные В позиционных системах счисления количественное значение цифры зависит от её позиции в числе. (x)р = аnpn + аn– 1 pn– 1 +. . . + а 1 p 1 + а 0 p 0. Примеры 11012 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 8 + 4 + 1 = 1310 , 1578 = 1 x 82 + 5 x 81 + 7 x 80 = 64 + 40 + 7 = 11110 , A 6 F 16 = 10 x 162 + 6 x 16*1 + 15 x 160 = 267110. • непозиционные В непозиционных системах счисления величина не зависит от положения цифры в записи числа, которую она обозначает. I 1 V 5 X 10 L C D 50 100 500 M 1000 Пример, VI = 5 + 1 = 6, IX = 10 - 1 = 9.

Перевод десятичных чисел в р-ную систему счисления : 1. Перевод целой части числа х - последовательно делить целую часть [х]10 , а затем все частные (получаемые при делении) на р , пока не получим в частном число меньшее р; 2. изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого; 3. Перевод дробной части числа х (мантиссы) числа- {x}10 , последовательно умножать исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p 4. изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т. д. , до последней цифры целой части; 5. результат будет иметь вид (х)р = [х]p, {х}p. Запасать представление: 12, 810 = ? 2. Переводим целую часть: 1210 =11002; переводим дробную часть: 0, 8 x 2 = 1, 6; 0, 6 x 2 = 1, 2; 0, 2 x 2 = 0, 4; 0, 4 x 2 = 0, 8; 0, 810 = 0, 1100. . . 2 ; результат перевода: 12, 810 = 1100, 1100. . . 2.

Перевод чисел в десятичную систему счисления : Пример 1. 2 Е 5. А 16= 2*162+14*161 +5*160+10*16 -1 =741, 62510 Пример 2. Перевести 1101. 101 в десятичную систему счисления: 1101. 1012=1*23+1*22+0*21+1*20+1*2 -1+0*2 -2+1*2 -3 =13, 62510

Перевод чисел между 2 -ной , 8 -ной и 16 -ной системами ОСНОВАНИЕ СИСТЕМЫ 10 2 8 16 0 0 0000 1 1 0001 2 — 010 — 011 0011 4 — 100 0100 5 — 101 0101 6 — 110 0110 7 — 111 0111 8 — — 1000 9 — — 1001 10=A 16 — — 1010 11=B 16 — — 1011 12=C 16 — — 1100 13=D 1 — — 1101 14=E 16 — — 1110 15=F 16 — — 1111 1. Из 2 -ной системы в 8 -ную (двоичновосьмеричное изображение): 0010 3 счисления 2. из 8 -ной системы в 2–ную (восьмерично-двоичное изображение):

Перевод чисел между 2 -ной , 8 -ной и 16 -ной системами счисления ОСНОВАНИЕ СИСТЕМЫ 10 2 8 16 0 0 0000 1 1 0001 2 — 010 0010 3 — 011 0011 4 — 100 0100 5 — 101 0101 6 — 110 0110 7 — 111 0111 8 — — 1000 9 — — 1001 10=A 16 — — 1010 11=B 16 — — 1011 12=C 16 — — 1100 13=D 1 — — 1101 14=E 16 — — 1110 15=F 16 — — 1111 3. из 2 -ной системы в 16 -ную (двоичношестнадцатеричное изображение): 4. из 16 -ной системы в 2 -ную (шестнадцатерично-двоичное изображение):

Действия в двоичной системе счисления. 1. Сложение. 2. Умножение. 3. Вычитание.

1. Сложение 0+0=0 0+1=1 1+0=1 1+1=10 11101+110 ? 10011 +1+1== 1 + 1 = 10 10 + 1 1 111 1=0 +10 110 + 1 11 _______

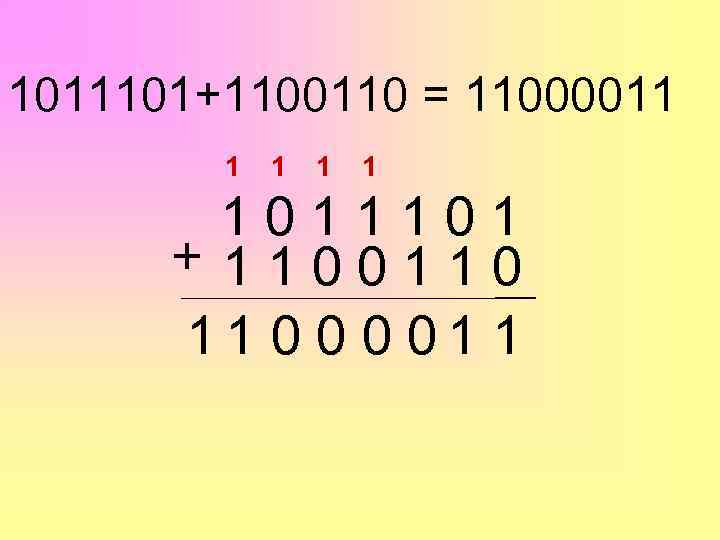1011101+1100110 = 11000011 1 1 1011101 + 1100110 11 0 01 1

2. Умножение. 0=0 0. 1=0 0. 0=0 1. 1=1 1 110 . 101= 11110 х 101 110 + 000 11110

• Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1). • Дополнительный код = обратный код + единица в младшем разряде. Пример1: 10011 двоичное число, 01100 обратный код этого числа, 01100+00001= 01101 дополнительный код этого числа; Пример2: 457 восьмеричное число, 320 - обратный код 320 +001=321 дополнительный код восьмеричного числа;

3. Вычитание разность 1000100 -100011= 100001 уменьшаемое 1000100 + 1011101 10100001 вычитаемое 0100011 1011100 - Обратный код + 1 1011101 - Дополнительный ко

разность 111101 -1001= 110100 уменьшаемое 111101 + 110111 1110100 вычитаемое 001001 110110 + 1 110111 - Обратный код - Дополнительный ко

Выполнить действия: 1011100 + 100101 = 10000001 10011101 – 11110 = 1111111 = 1001000111 110101. 1011

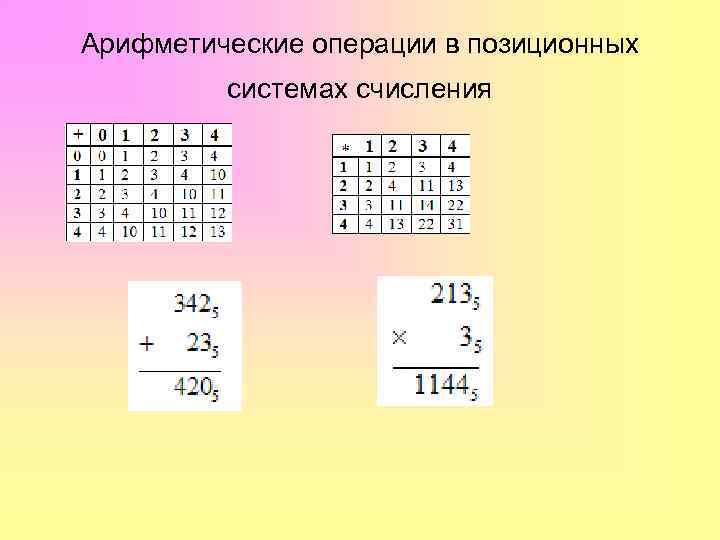Арифметические операции в позиционных системах счисления

Домашнее задание: Выполнить упражнения: 1. 101111 + 11101 2. 110011101 + 1000111 3. 101111 4. 11110110 – 1110100 5. 1110101111 – 10000010

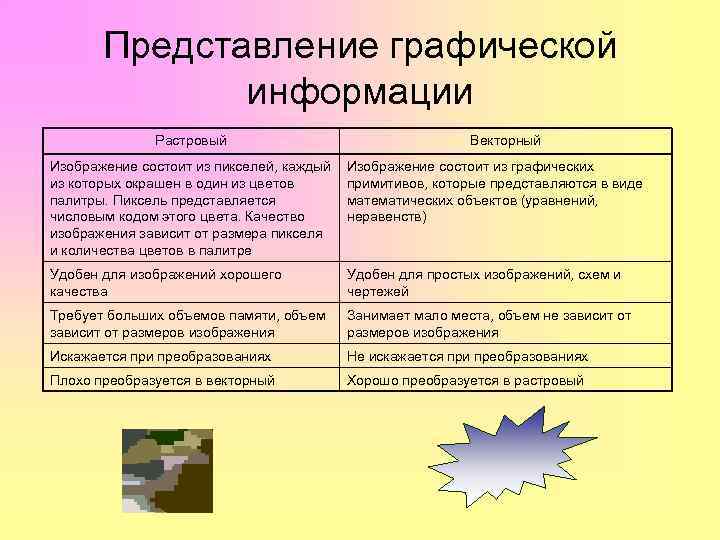Представление графической информации Растровый Векторный Изображение состоит из пикселей, каждый из которых окрашен в один из цветов палитры. Пиксель представляется числовым кодом этого цвета. Качество изображения зависит от размера пикселя и количества цветов в палитре Изображение состоит из графических примитивов, которые представляются в виде математических объектов (уравнений, неравенств) Удобен для изображений хорошего качества Удобен для простых изображений, схем и чертежей Требует больших объемов памяти, объем зависит от размеров изображения Занимает мало места, объем не зависит от размеров изображения Искажается при преобразованиях Не искажается при преобразованиях Плохо преобразуется в векторный Хорошо преобразуется в растровый

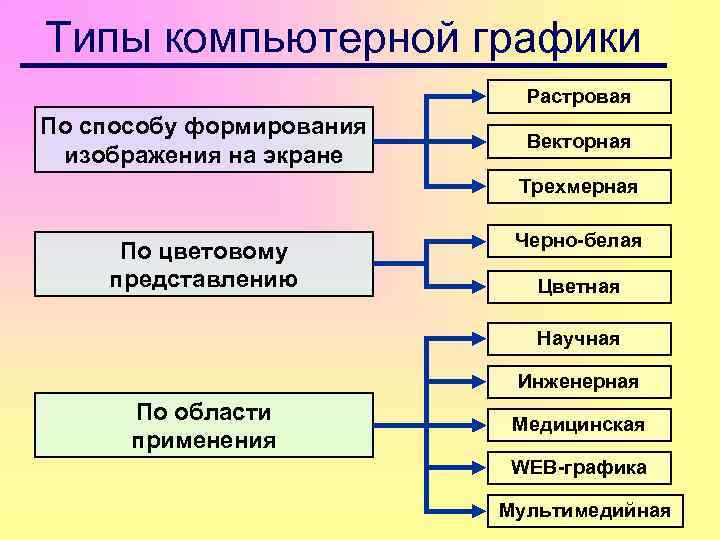Типы компьютерной графики Растровая По способу формирования изображения на экране Векторная Трехмерная По цветовому представлению Черно-белая Цветная Научная Инженерная По области применения Медицинская WEB-графика Мультимедийная

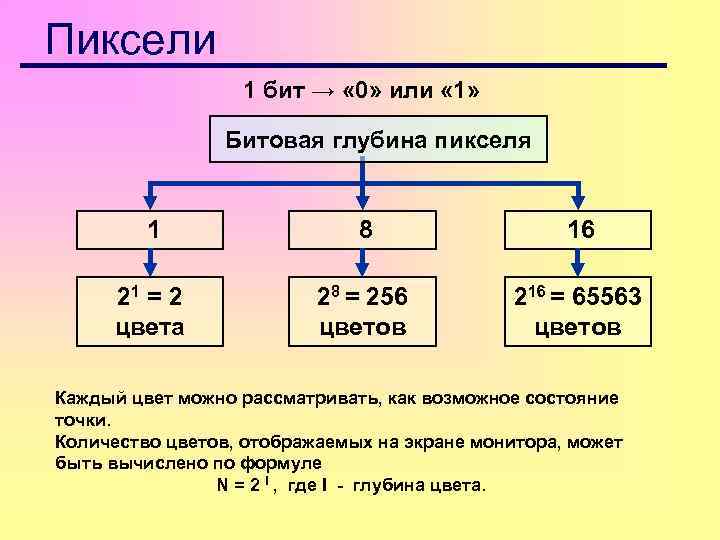Пиксели 1 бит → « 0» или « 1» Битовая глубина пикселя 1 8 16 21 = 2 цвета 28 = 256 цветов 216 = 65563 цветов Каждый цвет можно рассматривать, как возможное состояние точки. Количество цветов, отображаемых на экране монитора, может быть вычислено по формуле N = 2 I , где I - глубина цвета.

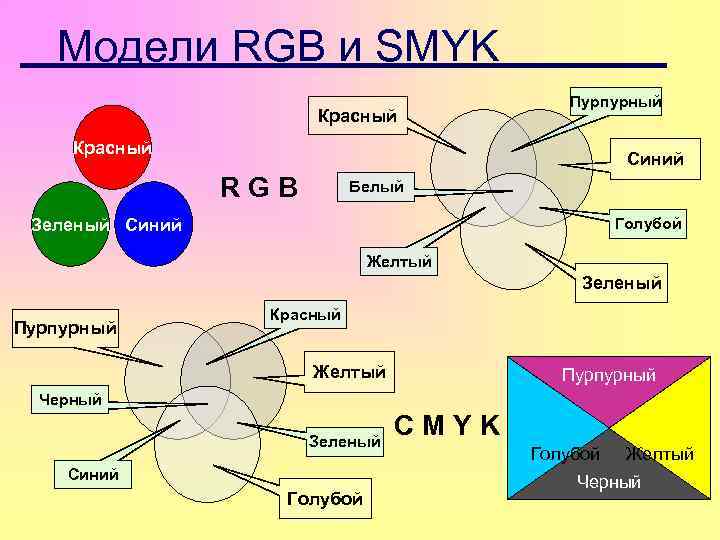Модели RGB и SMYK Красный Пурпурный Красный Синий RGB Белый Зеленый Синий Голубой Желтый Зеленый Пурпурный Красный Желтый Пурпурный Черный Зеленый Синий Голубой CMYK Голубой Желтый Черный

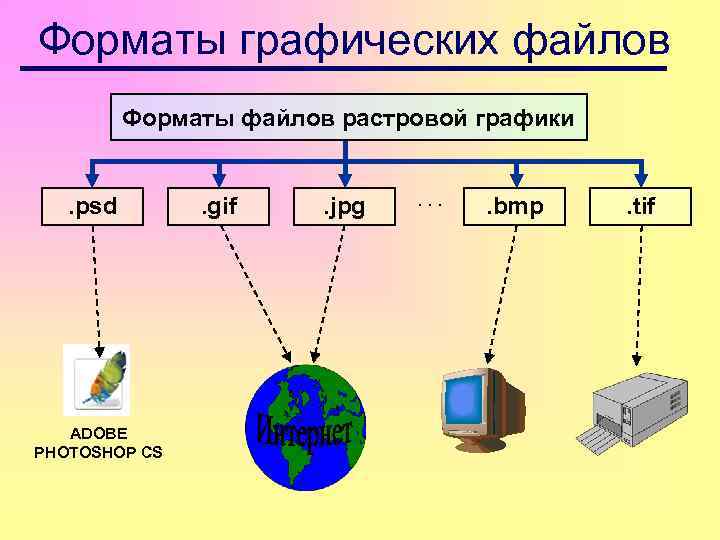Форматы графических файлов Форматы файлов растровой графики . psd ADOBE PHOTOSHOP CS . gif . jpg . . bmp . tif

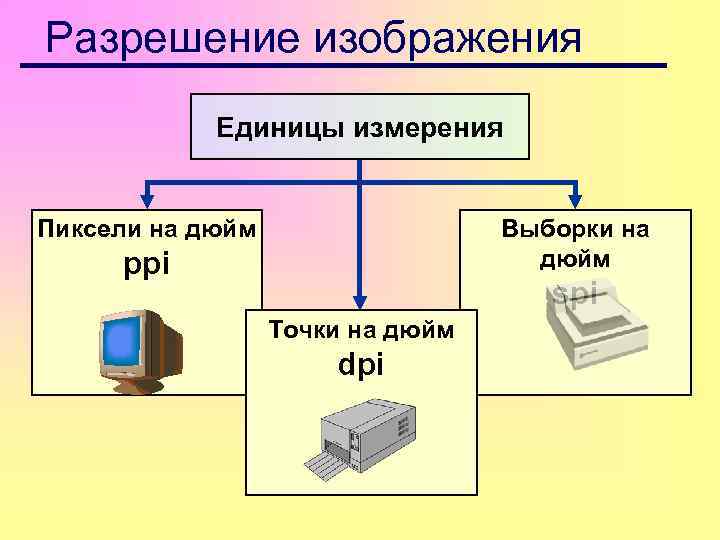Разрешение изображения Единицы измерения Пиксели на дюйм Выборки на дюйм ppi spi Точки на дюйм dpi

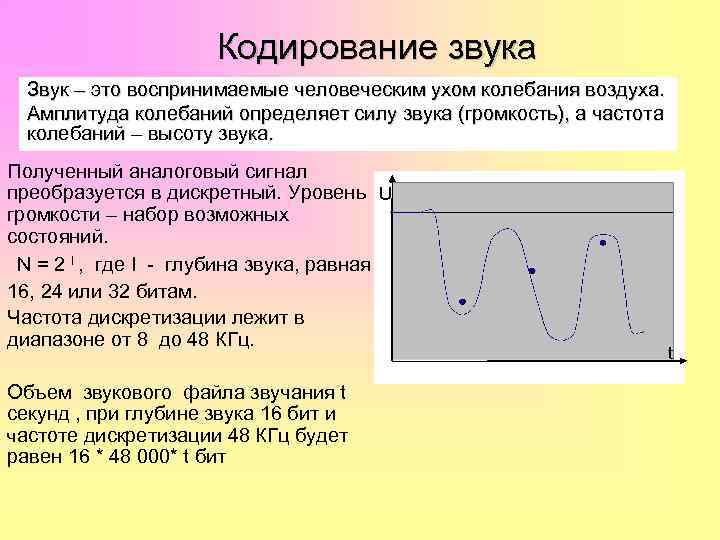Кодирование звука Звук – это воспринимаемые человеческим ухом колебания воздуха. Амплитуда колебаний определяет силу звука (громкость), а частота колебаний – высоту звука. Полученный аналоговый сигнал преобразуется в дискретный. Уровень U громкости – набор возможных состояний. N = 2 I , где I - глубина звука, равная 16, 24 или 32 битам. Частота дискретизации лежит в диапазоне от 8 до 48 КГц. Объем звукового файла звучания t секунд , при глубине звука 16 бит и частоте дискретизации 48 КГц будет равен 16 * 48 000* t бит t

Спасибо за внимание