КОДИРОВАНИЕ ПЕТУХОВ ДМИТРИЙ КОДИРОВАНИЕ

КОДИРОВАНИЕ ПЕТУХОВ ДМИТРИЙ

КОДИРОВАНИЕ • Кодирование представляет собой преобразование сообщения в последовательность некоторых символов. • Для этого устанавливают взаимооднозначное соответствие между сообщениями и символами, которое называется кодом.

КОДИРОВАНИЕ • При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). • Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией. • Совокупность кодовых комбинаций, обозначающих дискретные сообщения, образует код.

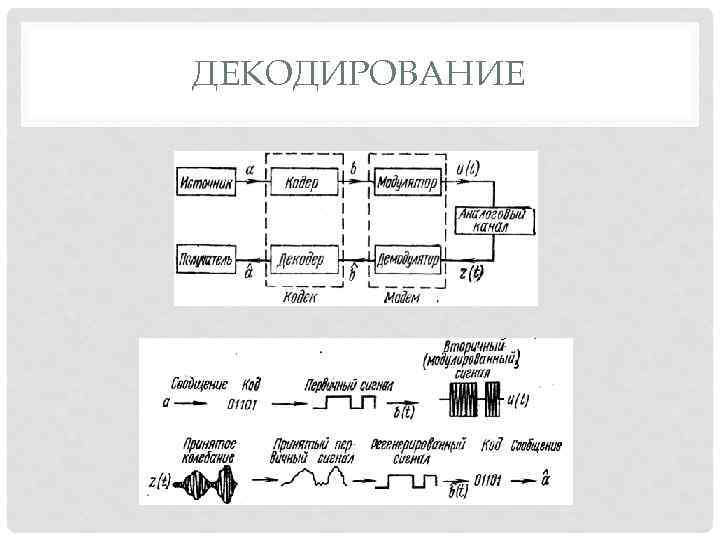
ДЕКОДИРОВАНИЕ • Декодирование – это процесс восстановления сообщения по принимаемым кодовым символам. • Устройства, осуществляющие кодирование и декодирование, называются соответственно кодером и декодером.

ДЕКОДИРОВАНИЕ

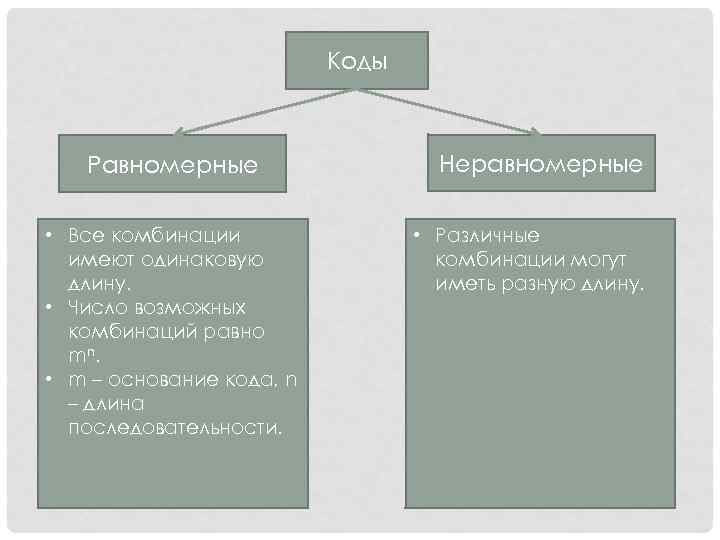
Коды Равномерные Неравномерные • Все комбинации • Различные имеют одинаковую комбинации могут длину. иметь разную длину. • Число возможных комбинаций равно mn. • m – основание кода, n – длина последовательности.

УСТРАНЕНИЕ ИЗБЫТОЧНОСТИ. МЕТОД ШЕННОНА-ФАНО • Этот метод требует упорядочения исходного множества символов по не возрастанию их частот. Затем выполняются следующие шаги: • а) список делится на 2 части так, чтобы суммы частот обеих частей были примерно или точно равны; • б) кодовым комбинациям первой части дописывается 1, второй части – 0; • в)анализируют первую часть: если она содержит только один символ, работа с ней заканчивается, и переходят к шагу г). Иначе переходят к шагу а) и обрабатывают первую часть как самостоятельный список; • г) анализируют вторую часть аналогично первой.

УСТРАНЕНИЕ ИЗБЫТОЧНОСТИ. МЕТОД ШЕННОНА-ФАНО Исходные символы Частоты символов Формируемый код a 0, 5 1 b 0, 25 01 c 0, 125 001 d 0, 125 000

УСТРАНЕНИЕ ИЗБЫТОЧНОСТИ. МЕТОД ХАФФМАНА • Исходное множество символов упорядочивается по не возрастанию частоты и выполняются следующие шаги: • 1) Объединение частот: две последние частоты складываются, соответствующие символы исключаются из списка и заменяются полученной суммой. Список вновь упорядочивается. Это повторяется до тех пор, пока не получится единица в результате суммирования и список не уменьшится до одного символа. • 2) Построение кодового дерева.

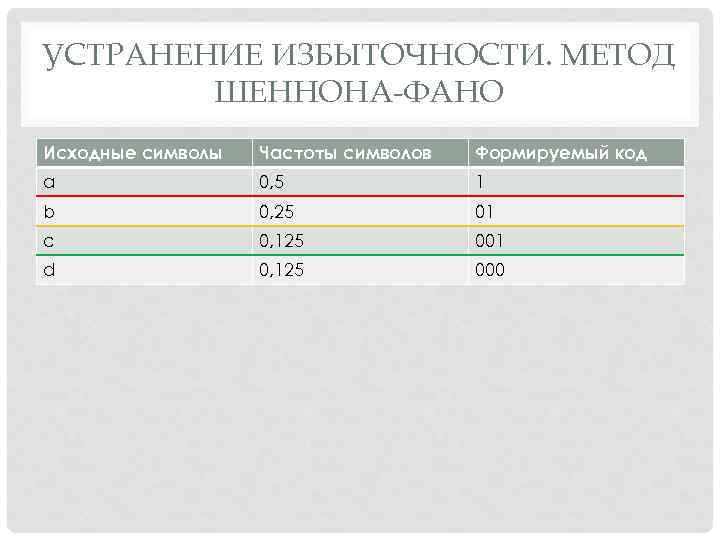
УСТРАНЕНИЕ ИЗБЫТОЧНОСТИ. МЕТОД ХАФФМАНА Исходные Частоты Этапы объединения Результат символы Первый Второй Третий a 0, 5 1 1 b 0, 25 0, 5 01 c 0, 125 0, 25 001 d 0, 125 000 0 d 0, 25 0, 125 0, 5 0 1 c 1 b 0, 125 a 0, 25 0, 5

КОДОВОЕ РАССТОЯНИЕ •

• Исходные символы Двоичные коды a 00 b 01 c 10 d 11

ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ •

ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ. КОД С ПРОВЕРКОЙ НА ЧЕТНОСТЬ Кодер Декодер • Этот метод служит для определения нечетного количества ошибок

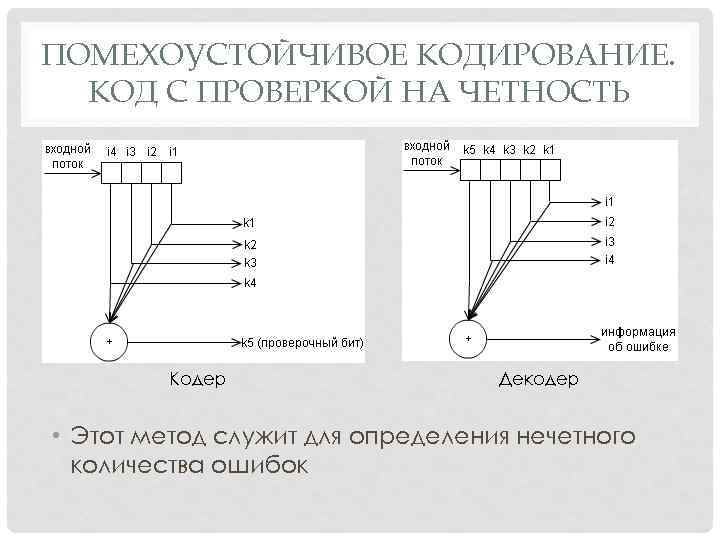
ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ. КОДЫ ХЭММИНГА • Каждый проверочный код представляет собой сумму по модулю 2 некоторой последовательности данных. • Проверочные символы располагаются на позициях, равных степеням двойки в порядке возрастания. Первый проверочный бит на 20=1, второй – 21=2, третий 22=4 и т. д.

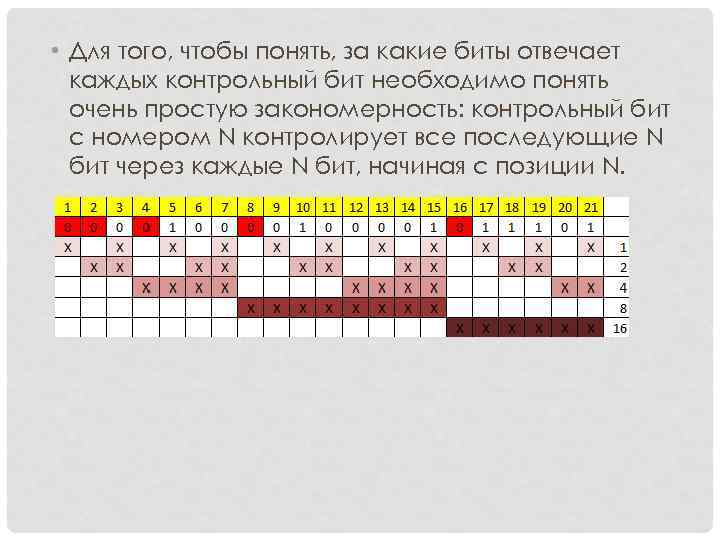
• Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N.

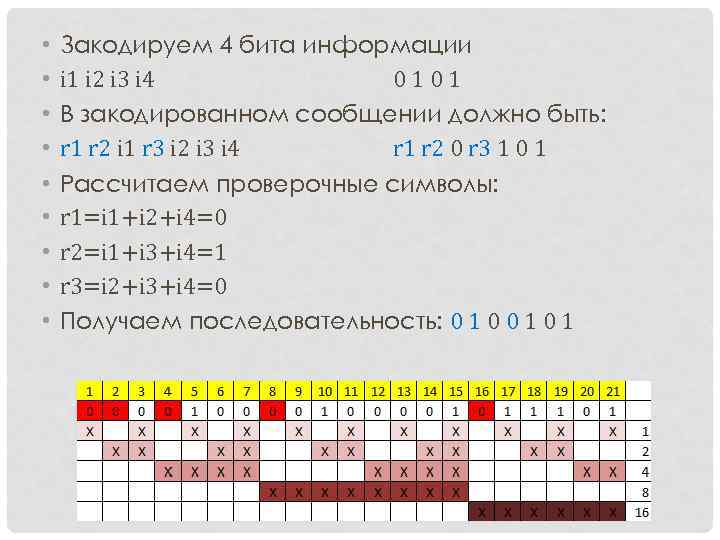
• Закодируем 4 бита информации • i 1 i 2 i 3 i 4 0101 • В закодированном сообщении должно быть: • r 1 r 2 i 1 r 3 i 2 i 3 i 4 r 1 r 2 0 r 3 1 0 1 • Рассчитаем проверочные символы: • r 1=i 1+i 2+i 4=0 • r 2=i 1+i 3+i 4=1 • r 3=i 2+i 3+i 4=0 • Получаем последовательность: 0 1 0 1

• Допустим, мы получили закодированное сообщение с ошибкой. • 0100001 • Заново вычисляются все контрольные биты. • r 1=0+0+1=1 • r 2=0+0+1=1 • r 3=0+0+1=1 • Получаем: • 1101001 • Сложив номера неправильных контрольных бит получаем позицию ошибки. • 1+4=5 • Инвертируем этот бит и получаем исходное сообщение. • 0101