Кодирование чисел в компьютере ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ

Кодирование чисел в компьютере

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ Так как любое целое число можно представить как вещественное, но с нулевой дробной частью, то можно было бы ограничиться представлением в компьютере вещественных чисел и реализацией арифметических действий над ними. Однако для ü эффективного использования памяти ü повышения скорости выполнения вычислений ü введения операции деления нацело с остатком ( в паскале DIV и MOD) Целые числа представляются специально для них предназначенными способами.

Введение специальных способов представления целых чисел оправдано тем, что часто в задачах, решаемых с помощью компьютера, многие действия сводятся к операциям над целыми числами. Например, ü в задачах экономического характера, где данными служат количества акций, сотрудников, деталей, транспортных средств и т. д. ü для обозначения даты и времени; ü для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. п.

Целые числа в компьютере хранятся в форме с фиксированной запятой (точкой). Способы компьютерного представления целых чисел отличаются: § количеством разрядов (8, 16, 32, 64 -х разрядные сетки) § наличием или отсутствием знакового разряда

БЕЗЗНАКОВОЕ ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ Все разряды ячейки отводятся под само число. 1. 8 -разрядная сетка 7 0 6 0 5 1 4 1 3 0 2 1 1 0 0 0 - разряды Пример: 5210= 1101002 Диапазон представляемых чисел: Аmin=00002=010 Amax=1111=28 -1=25510 Диапазон 0. . 255 В паскале – тип BYTE

2. 16 -разрядная сетка 10 9 8 7 6 5 4 3 2 1 0 15 14 13 12 11 0 0 -разряды 0 0 0 1 1 0 0 Диапазон представляемых чисел: Аmin=000000002=010 Amax=11111111=2161=6553510 Диапазон 0. . 65535 В паскале – тип WORD 3. 32 -разрядная сетка Аmin=0 Amax= 232 -1=4 294 967 295 4. 64 -разрядная сетка Аmin=0 Amax= 264 -1=18 446 744 073 709 551 615

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ Старший разрядной сетки отводится под знак: 0 – для положительного числа 1 – для отрицательных чисел 1. 8 -разрядная сетка Пример: 5210=1101002 7 0 6 0 Знак положительного числа Знак отрицательного числа 5 1 4 1 3 0 2 1 1 0 - разряды 0 0 Пример: -5210= -1101002 7 6 5 4 3 0 1 1 0 1 2 1 1 0 0 0

Диапазон представляемых чисел: Amax=1111111=27 -1=12710 Аmin= - 12810 В паскале – тип SHORTINT 2. 16 -разрядная сетка 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 0 0 0 0 1 1 0 0 Amax= =215 -1=3276710 Аmin= - 3276810 В паскале – тип INTEGER

Машинные коды чисел В компьютере с помощью применения специальных машинных кодов чисел все арифметические операции над числами сводятся к операциям арифметического сложения и сдвигу кодов.

Прямой машинный код Представление числа в привычной форме «знаквеличина» , когда первый бит n-разрядного слова знаковый, а остальные n-1 битов представляют цифровые разряды числа в двоичной системе счисления, называется прямым кодом двоичного числа. Прямой код целого числа полностью совпадает с записью самого числа в разрядной сетке компьютера. Прямой код отрицательного целого числа отличается от прямого кода соответствующего положительного числа содержимым знакового разряда Пример. Прямой код чисел Х=110112 и Y=-110112 в восьмиразрядной сетке имеет вид:

[Xпк]=00011011 [Yпк]=10011011 В системе прямых кодов существует два различных представления ноля: 0000 – положительный 0; 10000000 – отрицательный 0. Оба представления совершенно равноправны. Прямой код используется для хранения положительных и отрицательных чисел в запоминающих устройствах и для представления положительных чисел при выполнении операций в арифметических устройствах.

Дополнительный и обратный коды Для упрощения конструкций арифметических устройств вычислительных машин все арифметические операции, как правило, сводятся к сложению (операция вычитания) или к сериям сложений и сдвигов (операции умножения и деления). Замена операции вычитания (алгебраического сложения) на арифметическое сложение в компьютере осуществляется с помощью обратного и дополнительного кодов. Дополнительный код положительного числа совпадает с этим числом.

Объяснение сущности специальных кодов Рассмотрим на примере реверсивного счётчика для 3 -х разрядных десятичных чисел: 999 + 1= 1 000 -переполнение 002 … 497 разрядной сетки! 001 498 000 - 1 = -1 -по счётчику 999 – код – 1! 000 999 998 997 + - … 499 500 501 502 a + (-a) = 0 005 + (-005) = 000 005 + 995 = 1 000 995 – дополнительный код числа -005 5 – 2 = 5 + (-2) = 5 + 998 = 1 003 Если учесть, что единица 7 – 5 = 7 + (-5) = 7 + 995 = 1 002 переполнения теряется, то получаем правильные результаты Для устранения неоднозначности в кольце будем считать половину состояний (0 -499) кодами нуля и положительных чисел, а оставщуюся половину (500 -999) –кодами отрицательных чисел.

Дополнительный код для отрицательного числа равен дополнению его величины до числа, возникающего при переполнении разрядной сетки qn, где q – основание системы счисления, n – число разрядов в разрядной сетке. qn - называют константой образования дополнительного кода Операцию С = А – В, где А и В – целые положительные числа в любой системе счисления, можно представить в виде: С = А – В = А + (-В) + qn – qn = A +(qn- B)- qn А –первое слагаемое qn – В – дополнительный код числа –В (второго слагаемого) qn – константа, ликвидирующая единицу переполнения

Пример. А=9510, В=4310, n=2. Найти С=А-В. [-Bдк]=100 – 43 = 57 С = 95 + [-Bдк] – 100 = 95 + 57 – 100 = 152 – 100 = 52 Единицу в старшем разряде суммы можно просто зачеркивать. Необходимо найти способ получения дополнения произвольного числа Х до qn без использования вычитания: С = А – В = А + (-В) + qn – qn +1 -1 = A +(qn-1 - B)- qn + 1 Выражение qn – 1 – В определяет число В, получаемое заменой каждой цифры числа В на её дополнение до цифры q – 1. Так, 24510 + 24510 = 245 + 754 = 999. В называется обратным кодом числа В; qn-1 - константой образования обратного кода

Из обратного кода легко получить дополнительный код: В + В = qn-1 qn - В = В + 1 Дополнительный код получается путём добавления единицы к младшему разряду обратного кода Следовательно, дополнения двоичных чисел можно находить, минуя операцию вычитания. В обратном коде, как и в прямом, существует отрицательный и положительный ноль. Только в дополнительном коде ноль имеет единственное представление. Для данной длины разрядной сетки дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных. Договоримся обозначать прямой, обратный и дополнительный коды числа А через [Апк], [Аок], [Адк].

Пример. Найти прямой, обратный и дополнительный коды чисел А = 34 и В = - 34. [Апк]= 00102, [Аок]= 00102, [Адк]= 00102. [Впк]= 101000102, [Вок]= 11012, [Вдк]= 110111102. Алгоритм получения дополнительного кода отрицательного числа. 1. Модуль числа представить прямым кодом в k двоичных разрядах. 2. Значения всех бит инвертировать: все ноли заменить на единицы, а единицы на ноли (таким образом получается k-разрядный обратный код исходного числа); 3. К полученному обратному коду, трактуемому как k -разрядное неотрицательное двоичное число, прибавить единицу.

Примеры. 1. Дано отрицательное целое десятичное число M=-20. Представьте число в машинном коде в 16 разрядной сетке в двоичной и 16 -ричной системах счисления. М=-20=-101002 [Mпк]2=1. 0000 0001 0100 [M ок]2=1. 1111 1110 1011 [M дк]2=1. 1111 1110 1100 [M дк]16=FFEC

2. Дано целое число в виде 16 -ричного двоичного машинного кода. Определите десятичное значение данного числа: Ka=FFD 4 Первая цифра F, следовательно, число отрицательное и хранится в компьютере в форме дополнительного машинного кода. FFD 416 = [1. 1111 1101 0100 дк] -0. 0000 0001 [1. 1111 1101 0011 ок] – обратный код числа [Ka]ПК=[1. 0000 0010 1100 пк] – прямой двоичный код числа Тогда десятичное число а = - 101100 = - (32+8+4) = -44 – десятичное число

2 способ: через 16 -ричную систему счисления Ka=FFD 4 < 0, следовательно число а хранится в компьютере в дополнительном коде. Перейдем от дополнительного к прямому машинному коду: Так как дополнительный код для отрицательного числа равен дополнению его величины до числа, возникающего при переполнении разрядной сетки qn, то [Ka]ПК= 1000016 - FFD 416 = 002 С 16 Тогда десятичное число а = - 2 С 16= - (2. 161 + 12. 160) = = - 44

Действия над машинными кодами целых чисел Дано: десятичные числа А= 34 и В = 30 Найти: А+В, А – В, В – А в двоичных машинных кодах в 8 разрядной сетке. [Aпк] = [Аок] = [Адк] = 0. 010 00102 [-Aпк] = 1. 010 0010 [-Bпк] =1. 001 1110 [-Аок] = 1. 101 1101 [-Вок] = 1. 110 0001 [-Адк] =1. 101 1110 [-Вдк] = 1. 110 0010 [Впк] = [Вок] = [Вдк] = 0. 001 11102

[А + В]ДК = 0. 010 00102 + 0. 001 11102 = 010000002 А + В = 64 [А – В]ДК = 0. 010 00102 + 1. 110 00102 = 1 00000100 2 А–В=4 [В – А]ДК = 0. 001 11102 + 1. 101 11102 = 111111002 < 0, следовательно, это дополнительный код, нужно перевести его в прямой: [В – А]ОК = 111110112 [В – А]ПК = 100001002 В–А=-4

Действия над машинными кодами чисел с фиксированной точкой ( в 16 -ричной системе счисления) Дано: десятичные числа А= 34 и В = 30 Найти: А+В, А – В, В – А в 16 -ричных машинных кодах в 16 разрядной сетке. 1) А=34=2216 В=30=1 E 16 [KA]пк=002216 [KB]ПК=001 E 16 KA + KB = 0022 + 001 E = 004016 A + B =4. 161 + 0. 160 = 64 2) [K-B]ПК=801 E 16 [K-B]ДК=1000016 - 1 E 16 = FFE 216 KA + KB = 0022 + FFE 2 = 1 0004 А - В = 4. 160 = 4

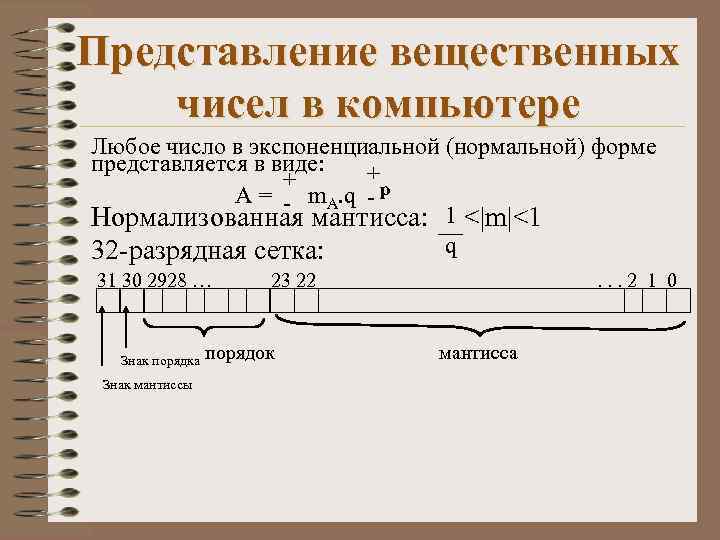Представление вещественных чисел в компьютере Любое число в экспоненциальной (нормальной) форме представляется в виде: + + A = - m. A. q - p Нормализованная мантисса: 1 <|m|<1 q 32 -разрядная сетка: 31 30 2928 … Знак порядка Знак мантиссы 23 22 порядок . . . 2 1 0 мантисса

В современных компьютерах машинная форма числа хранит не сам порядок, а его смещенное значение – характеристику числа. Это сделано для того, чтобы не хранить знак порядка и, значит, § облегчить действия над порядками; § увеличить диапазон представляемых чисел. 31 30 2928 … характеристика 23 22 . . . 2 1 0 мантисса Знак мантиссы Нормализованная мантисса всегда имеет целый разряд 0 и, следовательно, этот 0 в памяти компьютера не хранится, а только подразумевается. Это полезное техническое решение позволяет увеличить количество цифр и, следовательно, точность вычислений.

Примеры Вещественные числа представить как машинные коды чисел с плавающей точкой в 32 -разрядной сетке в 16 с/с: 9 7 а) А=32008, 5 б) В= - 32008, 5 в) С= 15 г) D= - 16 8 Найдем нормализованные мантиссы и характеристики этих чисел: а) А=32008, 5=7 D 08, 816=0, 7 D 088. 164 m. A=0, 7 D 088 Знак Характеристика Дробная часть мантиссы Нормализованная мантисса Характеристика px. A=4+40=4416=10001002 -0 - 1000100 - 0111 1101 0000 1000 0000 - 1111 1010 0001 0000 - 100 0011 KA= 0. 100 0011. 1111 1010 0001 00002 = = 43 FA 110016 > 0

б) B= -32008, 5= -7 D 08, 816= - 0, 7 D 088. 164 m. B= -0, 7 D 088 px. B=4+40=4416=10001002 Знак -1 Характеристика - 1000100 Дробная часть мантиссы - 0111 1101 0000 1000 0000 Нормализованная мантисса - 1111 1010 0001 0000 - 100 0011 Характеристика KB= 1. 1000011. 1111 1010 0001 00002 = = C 3 FA 110016 < 0

в) С= 15 14 =F, E 16 16 mc=0, FE 16 px. A=40+1=4116 Знак -0 Характеристика - 1000001 Дробная часть - 1111 1110 0000 мантиссы KC= 0. 1000001. 1111 1110 00002 = =41 FE 000016 > 0 в) D= - 9 = - 0, 916 16 m. B=0, 916 px. B=40+0=4016 Знак -1 Характеристика - 1000000 Дробная часть - 1001 0000 0000 мантиссы KD= 1. 1000000. 1001 0000 00002 = C 090000016 < 0

Действия над числами, представленными в экспоненциальной форме 1. Числа в экспоненциальной форме хранятся в памяти в прямом коде с нормализованными мантиссами. 2. Сложение кодов производится путём сложения мантисс только при одинаковых порядках (характеристиках) слагаемых. За общий выбирается наибольший порядок. 3. Алгоритмы операции алгебраического сложения после выравнивания характеристик зависят от знаков слагаемых. 4. Результаты в прямом коде нормализуются.

Примеры Выполнить операцию сложения машинных кодов чисел A и B с плавающей точкой в 32 -хразрядной сетке. В качестве ответа записать код результата (в 2 -ой и 16 -ой с/с) и соответствующее этому коду десятичное число 1) KA =43. F 34000 a) m. A=00. F 34 PAx=43 KB = C 1. A 13000 m. B=00. A 13 PBx=41 => P =2 => m. B =00. 00 A 13 – ПК _100. 00000 00. 00 A 13 FF. FF 5 ED b) m. A+m. B = 00. F 34 FF. FF 5 ED 100. F 29 ED > 0 => m. A+B = 00. F 29 ED

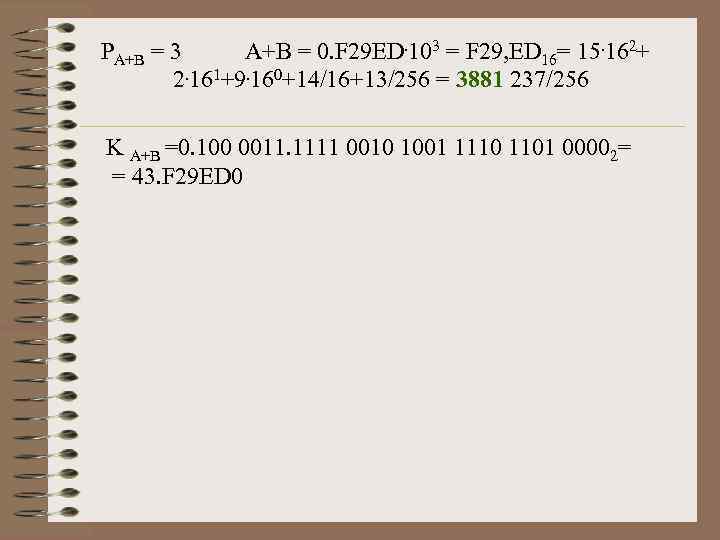PA+B = 3 A+B = 0. F 29 ED. 103 = F 29, ED 16= 15. 162+ 2. 161+9. 160+14/16+13/256 = 3881 237/256 K A+B =0. 100 0011. 1111 0010 1001 1110 1101 00002= = 43. F 29 ED 0