Кодирование целых положительных чисел Для представления целых чисел

Кодирование целых положительных чисел Для представления целых чисел в памяти компьютера используется дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Поддерживаются следующие типы данных: Integer величины входят в диапазон от – 32768 (– 215) до 32767 (215 – 1), для их хранения отводится 2 байта; типа Longint – в диапазоне от – 231 до 231 – 1 и размещаются в 4 байтах; типа Word – в диапазоне от 0 до 65535 (216 – 1), используется 2 байта. В памяти ЭВМ двоичные числа хранятся в регистрах, состоящих из 8 ячеек, т. е. минимальное двоичное число, которое можно разместить в памяти, должно быть восьмиразрядным. При этом в незаполненных ячейках регистра (в старших разрядах) записываются нули. Разряды нумеруются справа налево, начиная с 0. Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа получается следующим образом: число переводится в 2 c. c. , а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число. Пример 5, число 3710 = 1001012 типа Integer (2 байта – 16 знаков) имеет прямой код 00000100101, а типа Longing (4 байта) на 16 нулей больше. Для более компактной записи используется шестнадцатеричный код, для числа 3710 это 002516 и 0000002516.

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно равно: 2 n – 1. Пример 6. Определить диапазон чисел, которые могут храниться в оперативной памяти в формате целое неотрицательное число 1 байт. Минимальное число соответствует восьми нулям, хранящимся в восьми ячейках памяти, и равно нулю. Максимальное число соответствует восьми единицам, хранящимся в ячейках памяти и равно: = 1*28 – 1 = 25510. Следовательно, диапазон изменения целых неотрицательных чисел от 0 до 255.

Представление в ЭВМ отрицательных чисел В отличие от 10 c. c. в 2 c. c. отсутствуют специальные символы, обозначающие знак числа (+) или (–), поэтому для представления двоичных отрицательных чисел используется форма значения со знаком. Старший (левый) разряд метится как знаковый и содержит информацию о знаке числа: 1 – число отрицательное; 0 – число положительное. Остальные разряды отводятся под абсолютную величину числа. При представлении целых чисел в n-разрядном представлении со знаком максимальное положительное число (с учетом выделения одного разряда на знак) равно: А = 2 n– 1 – 1. Пример 7. Определить максимальное положительное число, которое может храниться в оперативной памяти в формате целое число со знаком 2 байта. А 10 = 216 -1 – 1 = 215 – 1 = 3276710.

При n-разрядном представлении отрицательного числа А дополнительным кодом старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число: 2 n– 1 – |A|. Чтобы число было положительным, должно выполняться условие: |A| = 2 n– 1. Следовательно, максимальное значение модуля числа А в n-разрядном представлении равно: |А| 2 n– 1. Тогда минимальное отрицательное число равно: А = – 2 n– 1. Пример. Определить диапазон чисел, которые могут храниться в памяти в формате целых чисел со знаком (для хранения таких чисел отводится 4 байта – 32 бита). Максимальное положительное целое число равно: А = 231 – 1 = 2 147 483 64710. Минимальное отрицательное целое число равно: А = – 231 = – 2 147 483 64810. Перевод отрицательных чисел осуществляется с помощью обратного дополнительного кода, он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие, по следующему алгоритму. Пример. Перевести число – 510 (1 байт): 1. Записать прямой код модуля числа |510| = 0000 01012. 2. Отбросить первый знаковый разряд. 3. Инвертировать все разряды числа (заменить единицы нулями, нули – единицами) 000 01012 111 10102. 4. Прибавить единицу к полученному коду: 111 10102 + 12 111 10112; 5. Восстановить единицу в знаковом разряде, ответ: – 510 = 1111 10112.

Представление в ЭВМ вещественных чисел В ЭВМ применяются две формы представления вещественных чисел: Естественная форма или форма с фиксированной запятой. Нормальная форма или форма с плавающей запятой. С фиксированной запятой все числа кодируются в виде последовательности цифр с постоянным положением запятой, отделяющей целую запись числа от дробной (25, 6789). Эта форма наиболее проста и естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. Диапазон значащих чисел Р в системе счисления с основанием N при наличии m разрядов в целой части числа и s разрядов в дробной части числа будет равен: N-s≤P≤Nm-N-s Пример, при N = 2, m = 10, s = 6, получим 0, 0156≤ P≤ 1024, т. е. в двоичной с. с. можно записать только 1024 числа, с целой частью, не более 10 цифр и дробной частью, не более 6 знаков. Диапазон чисел, записываемых в определенной с. с. формой с фиксированной запятой ограничен. Если в результате операции получится число, выходящее за допустимый предел, происходит переполнение разрядной сетки, и дальнейшие операции бессмысленны. В современных ЭВМ форма с фиксированной запятой используется как вспомогательная и только для целых чисел.

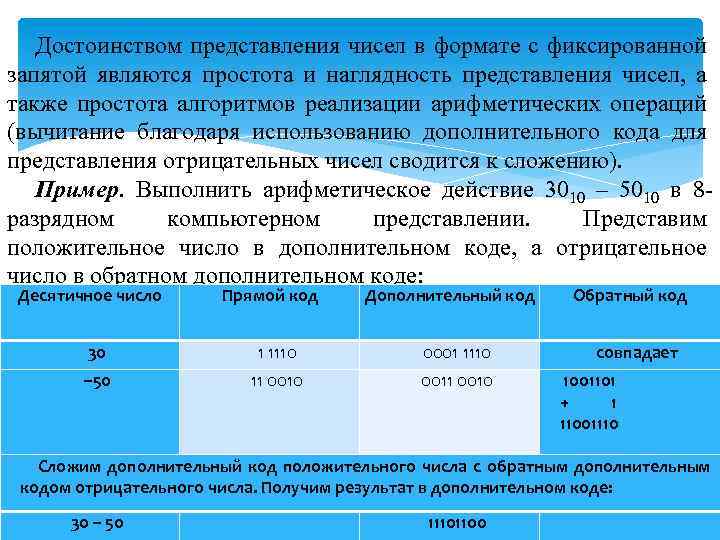Достоинством представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций (вычитание благодаря использованию дополнительного кода для представления отрицательных чисел сводится к сложению). Пример. Выполнить арифметическое действие 3010 – 5010 в 8 разрядном компьютерном представлении. Представим положительное число в дополнительном коде, а отрицательное число в обратном дополнительном коде: Десятичное число Прямой код Дополнительный код 30 1 1110 0001 1110 – 50 11 0010 0011 0010 Обратный код совпадает 1001101 + 1 11001110 Сложим дополнительный код положительного числа с обратным дополнительным кодом отрицательного числа. Получим результат в дополнительном коде: 30 – 50 11101100

Проведем проверку. Переведем полученный дополнительный код в десятичное число: 1) инвертируем дополнительный код: 0001 0011; 2) прибавим к полученному коду 1 и получим модуль отрицательного числа: 00010011+00000001= 00010100 3) переведем в десятичное число и припишем знак отрицательного числа: – 2010. Иной способ применяется для представления в памяти компьютера действительных чисел с плавающей запятой. В этом случае положение запятой в записи числа может изменяться. Любое действительное число можно привести в нормализованный справа вид М*10 р, где М – мантисса, р – порядок (целое), после запятой в мантиссе стоит не нуль. Пример, 1200010 = 0, 12*105, 0, 000410 = 0, 4*10– 3, числа в 2 с. с. 11, 012 = 0, 1101*22, 0, 0112 = 0, 11*2 -1. Место, отводимое для числа с плавающей запятой, делится на три поля. Одно поле содержит знак числа, второе содержит знак и значение порядка, а третье значение мантиссы. Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.

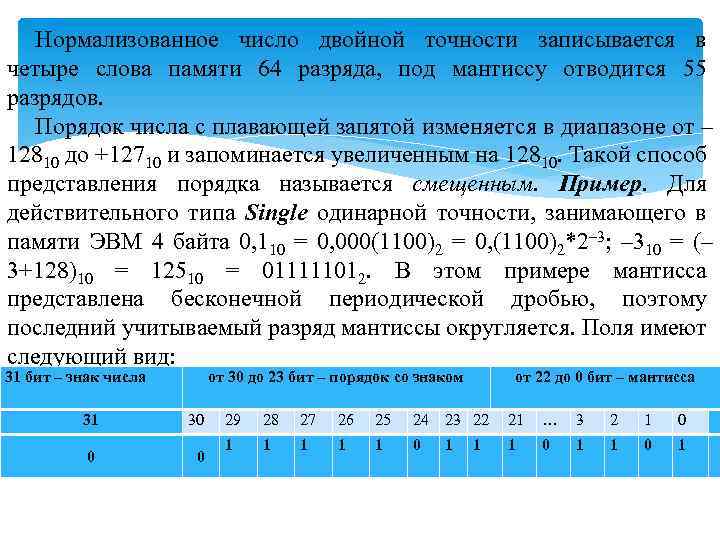Нормализованное число двойной точности записывается в четыре слова памяти 64 разряда, под мантиссу отводится 55 разрядов. Порядок числа с плавающей запятой изменяется в диапазоне от – 12810 до +12710 и запоминается увеличенным на 12810. Такой способ представления порядка называется смещенным. Пример. Для действительного типа Single одинарной точности, занимающего в памяти ЭВМ 4 байта 0, 110 = 0, 000(1100)2 = 0, (1100)2*2– 3; – 310 = (– 3+128)10 = 12510 = 011111012. В этом примере мантисса представлена бесконечной периодической дробью, поэтому последний учитываемый разряд мантиссы округляется. Поля имеют следующий вид: 31 бит – знак числа от 30 до 23 бит – порядок со знаком 31 30 0 0 от 22 до 0 бит – мантисса 29 28 27 26 25 24 23 22 21 … 3 2 1 0 1 1 0 1 1

Пример. 49, 510=110001, 12=0, 11000112*26; 610=(6+128)10=13410=100001102. При сложении и вычитании чисел в формате с плавающей запятой сначала производится подготовительная операция выравнивания порядков. Порядок меньшего (по модулю) числа увеличивается до величины порядка большего (по модулю) числа. Для того чтобы величина числа не изменилась, мантисса уменьшается в такое же количество раз (сдвигается в ячейке памяти вправо на количество разрядов, равное разности порядков чисел). Теперь операции сложения и вычитания чисел сводятся к сложению или вычитанию мантисс. После выполнения арифметической операции для приведения полученного числа к стандартному формату с плавающей запятой производится нормализация, то есть мантисса сдвигается влево или вправо так, чтобы ее первая значащая цифра попала в первый разряд после запятой. Пример. Произвести сложение чисел 0, 1 23 и 0, 1 25 в формате с плавающей запятой. Произведем выравнивание порядков и сложение мантисс: 0, 001 25+0, 100 25=0, 101 25 При умножении чисел в формате с плавающей запятой порядки складываются, а мантиссы перемножаются. При делении из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Пример. Произвести умножение чисел 0, 1 23 и 0, 1 25 в формате с плавающей запятой. После умножения будет получено число 0, 01 28, которое после нормализации примет вид 0, 1 27.

Кодирование текстовых данных При вводе документов, текстов программ вводимые символы (буквы, цифры, знаки) кодируются определенными комбинациями из восьми нулей и единиц и, наоборот – при выводе их для чтения человеком (на монитор или принтер) по коду символа строится изображение символа. При двоичном кодировании текстовой информации каждому символу назначается код – последовательность из фиксированного количества нулей и единиц с взаимно однозначным соответствием. Оптимальное количество символов, которые используются при наборе различных текстов, равно примерно 200 (буквы латинские и русские, заглавные и строчные, знаки препинания, цифры, математические знаки, элементы псевдографики). Такое количество символов в двоичной системе может быть закодировано последовательностью из 8 бит (28 = 256), 1 байтом. Наиболее распространенной международной восьмиразрядной кодировкой является ASCII код – стандартный американский код для обмена информацией. Таблица ASCII-кодов состоит из трех частей. Первые две части общеприняты во всем мире.

1. От 0 до 32 коды зарезервированы для различных управляющих символов (возврат каретки, табуляция, отмена операции и т. п. ). 2. От 33 до 127 коды зарезервированы для букв латинского алфавита, строчные и прописные, знаки препинания, цифры, математические знаки. 3. От 128 до 255 коды представляют собой расширенные ASCII коды, для национальных алфавитов и специальных символов. В таблице знакам алфавита ставятся в соответствие шестнадцатеричные числа по правилу: первая – номер столбца, вторая – номер строки. Например, ф – код E 4. К сожалению, в настоящее время существуют пять различных кодировок кириллицы КОИ 8 -Р, Windows (CP 1251 – Code Page), MSDOS, Macintosh и ISO, что вызывает дополнительные трудности при работе с русскоязычными документами. Помимо восьмиразрядной системы кодирования символьной информации разработана система шестнадцатиразрядного кодирования символов UNICODE, она является универсальной. Позволяет закодировать 216 = 65536 различных символов, практически все алфавиты нашей планеты. Расчет объема текстовой информации сводится к вычислению произведения количества символов в тексте на число разрядов двоичного кода, необходимого для кодирования одного символа.

Кодирование цветовой и графической информации Графические изображения, хранящиеся в аналоговой (непрерывной) форме на бумаге, фото- и кинопленке, могут быть преобразованы в цифровой компьютерный формат путем пространственной дискретизации. Это реализуется путем сканирования, результатом которого является растровое изображение. Растровое изображение состоит из отдельных точек (пикселей), каждая из которых может иметь свой цвет. Качество растрового изображения определяется его разрешением (количеством точек по вертикали и по горизонтали) и используемой палитрой цветов (16, 256, 65536 цветов и более). Из формулы (2. 2) можно определить, какое количество бит информации необходимо выделить для хранения цвета точки (глубину цвета) для каждой палитры цветов. Пример. Определить глубину цвета в графическом режиме, в котором палитра состоит из 65536 цветов. I = log 2 65536= 16 бит. В современных компьютерах используются различные графические режимы экрана монитора, каждый из которых характеризуется разрешающей способностью и глубиной цвета. Для реализации каждого графического режима требуется определенный объем видеопамяти компьютера.

Пример. Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора с разрешающей способностью 1024 768 точек и палитрой из 65 536 цветов. Глубина цвета составляет: I = log 265 536 = 16 бит. Количество точек изображения равно: 1024 768 = 786 432. Требуемый объем видеопамяти равен: 16 бит 786 432 = 12 582 912 бит 1, 2 Мбайт. Важнейшими характеристиками монитора являются размеры его экрана, которые задаются величиной его диагонали в дюймах (15", 17", 21" и так далее) и размер точки экрана (0, 25 мм или 0, 28 мм), а разрешающая способность экрана монитора задается количеством точек по вертикали и горизонтали (640 480, 800 600 и так далее). Следовательно, для каждого монитора существует физически максимально возможная разрешающая способность экрана.

Пример. Определить максимально возможную разрешающую способность экрана для монитора с диагональю 15" и размером точки экрана 0, 28 мм. Выразим размер диагонали в сантиметрах 2, 54 см 15 = 38, 1 см. Определим соотношение между высотой и шириной экрана для режима 1024 768 точек: 768 / 1024 = 0, 75. Определим ширину экрана. Пусть ширина = L, тогда высота = 0, 75 L. По теореме Пифагора имеем: L 2 + (0, 75 L)2 = 38, 12, 1, 5625 L 2 = 1451, 61, L 2 929, L 30, 5 см. Количество точек по ширине экрана равно: 305 мм / 0, 28 мм = 1089. Максимально возможным разрешением экрана монитора является 1024 x 768. Цветное растровое изображение формируется в соответствии с цветовой моделью RGB, в которой тремя базовыми цветами являются Red (красный), Green (зеленый) и Blue (синий). В режиме True Color (3 байта = 224 16, 5 млн. различных цветов и оттенков) интенсивность каждого цвета задается 8 -битным двоичным кодом, который часто для удобства выражают в шестнадцатеричной системе счисления. В этом случае используется следующий формат записи RRGGBB. Первый байт определяет интенсивность красной составляющей, второй – зеленой, третий – синей. Белый цвет кодируется полными тремя байтами 255, 255 или в двоичной системе 11111111, 1111. Черный цвет – отсутствием всех цветов 0, 0, 0. Красный цвет может быть темным – 120, 0, 0 или ярко красным 255, 0, 0.

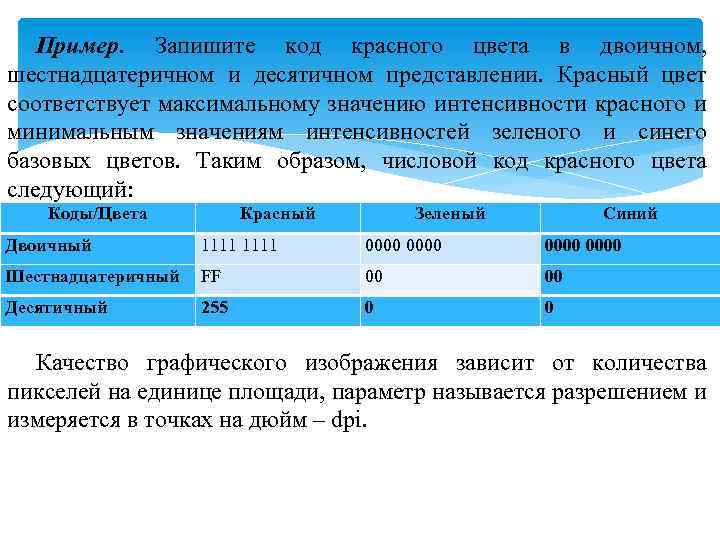Пример. Запишите код красного цвета в двоичном, шестнадцатеричном и десятичном представлении. Красный цвет соответствует максимальному значению интенсивности красного и минимальным значениям интенсивностей зеленого и синего базовых цветов. Таким образом, числовой код красного цвета следующий: Коды/Цвета Красный Зеленый Синий Двоичный 1111 0000 Шестнадцатеричный FF 00 00 Десятичный 255 0 0 Качество графического изображения зависит от количества пикселей на единице площади, параметр называется разрешением и измеряется в точках на дюйм – dpi.

Пример. Сканируется цветное изображение размером 10 10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл. Разрешающая способность сканера 600 dpi означает, что на отрезке длиной 1 дюйм сканер способен различить 600 точек. Переведем разрешающую способность сканера из точек на дюйм (1 дюйм = 2, 54 см) в точки на сантиметр: 600 dpi / 2, 54 = 236 точек/см. Следовательно, размер изображения в точках составит 2360 точек. Общее количество точек изображения равно: 2360 = 5 569 600. Информационный объем файла равен: 32 бита 5569600 = 178 227 200 бит 21 Мбайт.

Кодирование звуковой информации В аналоговой форме звук представляет собой волну с непрерывно меняющейся амплитудой и частотой. При преобразовании звука в цифровую форму производится временная дискретизация, при которой в определенные моменты времени амплитуда звуковой волны измеряется и квантуется, то есть ей присваивается определенное значение из некоторого фиксированного набора. Данный метод называется еще импульсно-кодовой модуляцией РСМ. Преобразование непрерывной звуковой волны в последовательность звуковых импульсов различной амплитуды производится с помощью аналого-цифрового преобразователя, размещенного на звуковой плате. 16 -битные звуковые карты обеспечивают возможность кодирования 65536 различных уровней громкости или 16 -битную глубину кодирования звука. Качество кодирования звука зависит и от частоты дискретизации – количества измерений уровня сигнала в единицу времени. Эта величина может принимать значения от 8 до 48 к. Гц.

Пример. Оцените информационный объем высококачественного стереоаудиофайла длительностью звучания 1 минута, если глубина кодирования 16 бит, а частота дискретизации 48 к. Гц. Информационный объем звукового файла длительностью в 1 секунду равен: 16 бит 48 000 2 = 1 536 000 бит = 187, 5 Кбайт. Информационный объем звукового файла длительностью 1 минута равен: 187, 5 Кбайт/с 60 с 11 Мбайт.