Скачать презентацию Knowledge Representation Grigoris Antoniou FORTH-ICS Greece 1 Lugano
b8a6102c9b19b41f2017a71fa29ea85d.ppt
- Количество слайдов: 164
Knowledge Representation Grigoris Antoniou FORTH-ICS, Greece 1 Lugano course, November 2009 Knowledge Representation
Week’s Objectives l l 2 Get an idea of what Knowledge Representation (KR) is about Get a taste of the area through a couple of concrete languages/systems See how KR plays a role in contemporary ICT areas: Web, pervasive computing Get motivated for more? Lugano course, November 2009 Knowledge Representation
Week’s Outline I. III. IV. V. 3 KR Basics KR on the Web: Semantic Web Defeasible Reasoning KR in e-Commerce and Pervasive Computing Summary Lugano course, November 2009 Knowledge Representation
Part I: Knowledge Representation Basics 4 Lugano course, November 2009 Knowledge Representation
Artificial Intelligence l The design and study of systems that behave intelligently – – l Critical: – – 5 Focus on hard problems, often with no, or very inefficient full algorithmic solution Focus on problems that require “reasoning” (“intelligence”) and a large amount of knowledge about the world Represent knowledge about the world Reason with these representations to obtain meaningful answers/solutions Lugano course, November 2009 Knowledge Representation
Symbolic Knowledge Representation: Basic Assumptions l l 6 Important objects (collections of objects) and their relationships are represented explicitly by internal symbols Symbolic manipulation of internal symbolic representations achieves results meaningful in the real world. Lugano course, November 2009 Knowledge Representation
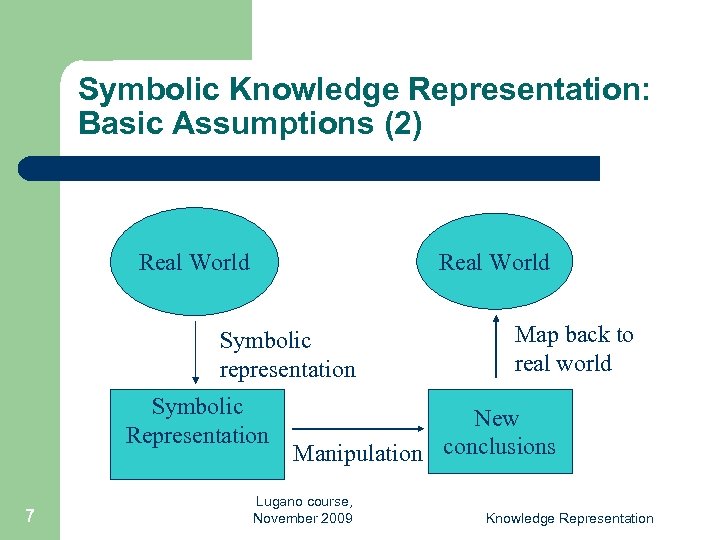Symbolic Knowledge Representation: Basic Assumptions (2) Real World Symbolic representation Symbolic Representation 7 Map back to real world New Manipulation conclusions Lugano course, November 2009 Knowledge Representation
KR Goals Find representations that are: l Rich enough to express the important knowledge relevant to the problem at hand l Close to problem at hand: compact, natural, maintainable l Amenable to efficient computation 8 Lugano course, November 2009 Knowledge Representation
Representational Adequacy l Consider the following facts: – – l l 9 Most children believe in Santa. John will have to finish his assignment before he can start working on his project. Can all be represented as a string! But hard then to manipulate and draw conclusions. How do we represent these formally in a way that can be manipulated in a computer program? Lugano course, November 2009 Knowledge Representation
Well-defined Syntax & Semantics l Precise syntax: what can be expressed in the language – – l 10 Formal language, unlike natural language Prerequisite for precise manipulation through computation Precise semantics: formal meaning of expression Lugano course, November 2009 Knowledge Representation
Naturalness of Expression l l Also helpful if our representation scheme is quite intuitive and natural for human readers! Could represent the fact that my car is red using the notation: – – l 11 “xyzzy ! Zing” where xyzzy refers to redness, Zing refers to by car, and ! used in some way to assign properties. But this wouldn’t be very helpful. . . Lugano course, November 2009 Knowledge Representation
Inferential Adequacy l Representing knowledge not very interesting unless you can use it to make inferences: – Draw new conclusions from existing facts. l – l 12 “If its raining John never goes out” + “It’s raining today” so. . . Come up with solutions to complex problems, using the represented knowledge. Inferential adequacy refers to how easy it is to draw inferences using represented knowledge. Lugano course, November 2009 Knowledge Representation
Inferential Efficiency l l You may be able, in principle, to make complex deductions, but it may be just too inefficient. The basic tradeoff of all KR: – l The eternal quest of KR: – 13 Generally the more complex the possible deductions, the less efficient will be the reasoning process (in the worst case). Need representation and inference system sufficient for the task, without being hopelessly inefficient. Lugano course, November 2009 Knowledge Representation
Inferential Adequacy (2) l 14 Representing everything as natural language strings has good representational adequacy and naturalness, but very poor inferential adequacy. Lugano course, November 2009 Knowledge Representation
Requirements for KR Languages: Summary – – – Representational Adequacy Clear syntax/semantics Inferential adequacy Inferential efficiency Naturalness In practice no one language is perfect, and different languages are suitable for different problems. 15 Lugano course, November 2009 Knowledge Representation
Why Reasoning? Example: Patient x is allergic to medication m Anybody allergic to medication m is also allergic to medication n Is it ok to prescribe n for x? l Reasoning uncovers implicit knowledge not represented explicitly – 16 Beyond database systems technology Lugano course, November 2009 Knowledge Representation
Syntactic vs Semantic Reasoning Semantic reasoning: – – – Sentences P 1, …, Pn entail sentence P iff the truth of P is implicit in the truth of P 1, …, Pn Or: if the world satisfies P 1, …, Pn then it must also satisfy P Reasoning usually done by humans Syntactic reasoning: – – 17 Sentences P 1, …, Pn infer sentence P iff there is a syntactic manipulation of P 1, …, Pn that results in P Reasoning done by humans and machines Lugano course, November 2009 Knowledge Representation
Reasoning: Soundness and Completeness l Sound (syntactic) reasoning: – – l Complete (syntactic) reasoning: – – l If P is entailed semantically by P 1, …, Pn then it can also be inferred All semantically valid conclusions can be drawn Usually interested in sound and complete reasoning – 18 If P is inferred by P 1, …, Pn then it is also entailed semantically Only semantically valid conclusions are drawn But sometimes we have to give up one for the sake of efficiency (usually completeness) Lugano course, November 2009 Knowledge Representation
Main KR Approaches l Logic-Based – – l Frames / Semantic Networks / Objects – l Focus on structure of objects Rule-based systems – – 19 Focus on clean, mathematical semantics: declarativity Explainability Focus on efficiency A B in logic and rule-based systems Lugano course, November 2009 Knowledge Representation
The Landscape of KR l Predicate logic (first order logic) and its sublanguages – – – l Predicate logic (first order logic) extensions – – – l Modal and epistemic logics Temporal logics Spatial logics Inconsistency-tolerant logics: – – 20 Logic programming, (pure) Prolog Description logics Web ontology languages Paraconsistency Nonmonotonic reasoning Lugano course, November 2009 Knowledge Representation
The Landscape of KR (2) l Representing vagueness – – – l Planning and reasoning about action – l 21 Probabilistic logics Bayesian networks Markov chains Extensions of logic to reason about the prerequisites and effects of actions … Lugano course, November 2009 Knowledge Representation
Part II: KR on the Web: Semantic Web 22 Lugano course, November 2009 Knowledge Representation
The Semantic Web l l 23 The Semantic Web vision RDF OWL Rules Lugano course, November 2009 Knowledge Representation
Today’s Web l Most of today’s Web content is suitable for human consumption – l Typical Web uses today people’s – 24 Even Web content that is generated automatically from databases is usually presented without the original structural information found in databases seeking and making use of information, searching for and getting in touch with other people, reviewing catalogs of online stores and ordering products by filling out forms Lugano course, November 2009 Knowledge Representation
Keyword-Based Search Engines l Current Web activities are not particularly well supported by software tools – l 25 Except for keyword-based search engines (e. g. Google, Alta. Vista, Yahoo) The Web would not have been the huge success it was, were it not for search engines Lugano course, November 2009 Knowledge Representation
Problems of Keyword-Based Search Engines l l l 26 High recall, low precision. Low or no recall Results are highly sensitive to vocabulary Results are single Web pages Human involvement is necessary to interpret and combine results Results of Web searches are not readily accessible by other software tools Lugano course, November 2009 Knowledge Representation
On HTML l l l 27 Web content is currently formatted for human readers rather than programs HTML is the predominant language in which Web pages are written (directly or using tools) Vocabulary describes presentation Lugano course, November 2009 Knowledge Representation
An HTML Example
But note that we do not offer consultation during the weeks of the State Of Origin games. 28 Lugano course, November 2009 Knowledge Representation
Problems with HTML l l Humans have no problem with this Machines (software agents) do: – – – 29 How distinguish therapists from the secretary, How determine exact consultation hours They would have to follow the link to the State Of Origin games to find when they take place. Lugano course, November 2009 Knowledge Representation
A Better Representation
Semantic Web Technologies l l 31 Explicit Metadata Ontologies Logic and Inference Agents Lugano course, November 2009 Knowledge Representation
Explicit Metadata l l This representation is far more easily processable by machines Metadata: data about data – l 32 Metadata capture part of the meaning of data Semantic Web does not rely on text-based manipulation, but rather on machineprocessable metadata Lugano course, November 2009 Knowledge Representation
Ontologies The term ontology originates from philosophy l The study of the nature of existence Different meaning from computer science l An ontology is an explicit and formal specification of a conceptualization 33 Lugano course, November 2009 Knowledge Representation
Typical Components of Ontologies l Terms denote important concepts (classes of objects) of the domain – l Relationships between these terms: typically class hierarchies – – l a class C to be a subclass of another class C' if every object in C is also included in C' e. g. all professors are staff members Value restrictions – 34 e. g. professors, staff, students, courses, departments e. g. only faculty members can teach courses Lugano course, November 2009 Knowledge Representation
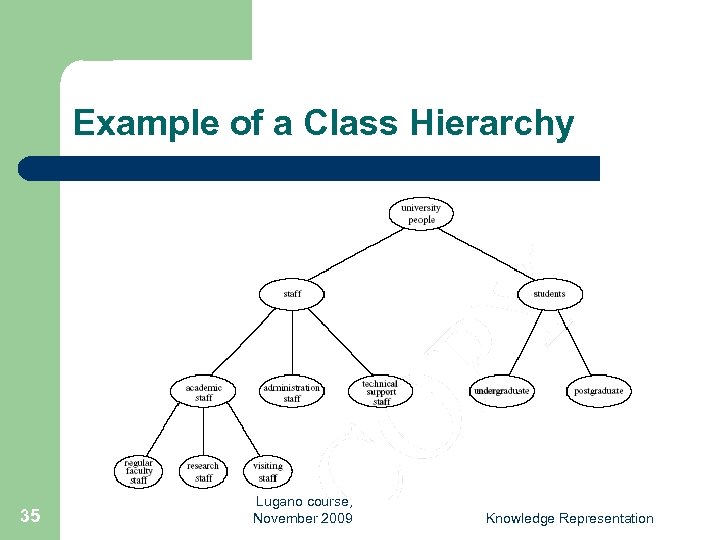Example of a Class Hierarchy 35 Lugano course, November 2009 Knowledge Representation
The Role of Ontologies on the Web l Ontologies provide a shared understanding of a domain: semantic interoperability – – l 36 overcome differences in terminology mappings between ontologies Ontologies are useful for the organization and navigation of Web sites Lugano course, November 2009 Knowledge Representation
Typical Ontology Use Case: Image Search § § § 37 A person searches for photos of an “orange ape” An image collection of animal photographs contains snapshots of orang -utans. The search engine finds the photos, despite the fact that the words “orange” and “ape” do not appear in annotations Lugano course, November 2009 Knowledge Representation
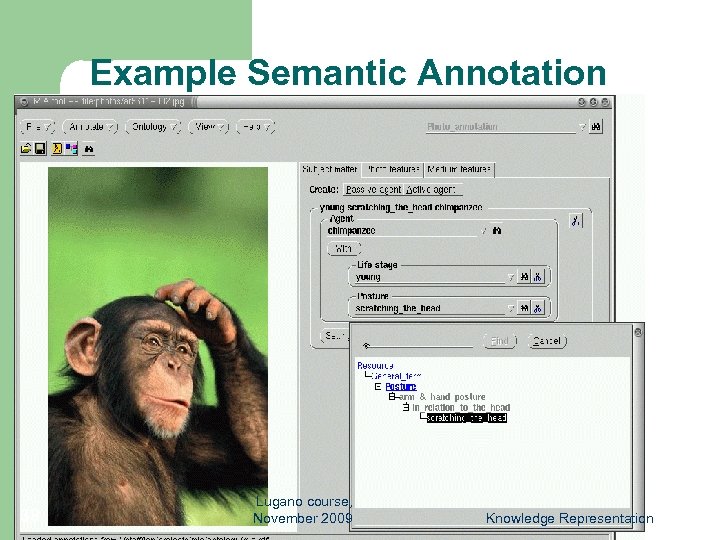Example Semantic Annotation 38 Lugano course, November 2009 Knowledge Representation
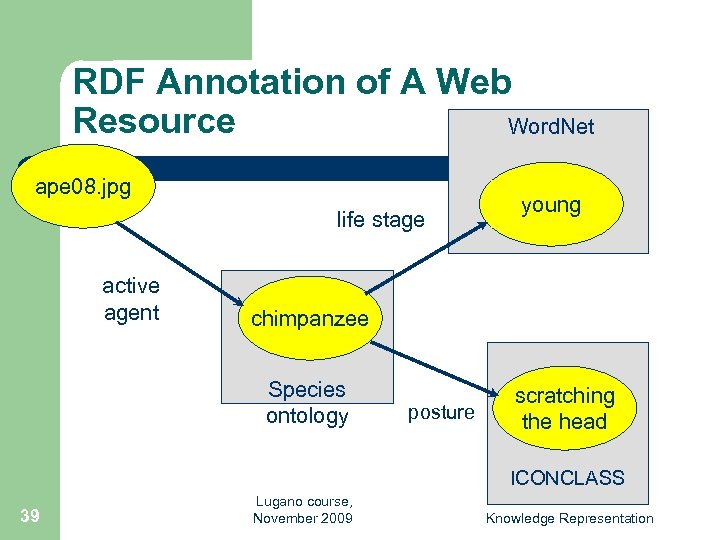RDF Annotation of A Web Resource Word. Net ape 08. jpg life stage active agent young chimpanzee Species ontology posture scratching the head ICONCLASS 39 Lugano course, November 2009 Knowledge Representation
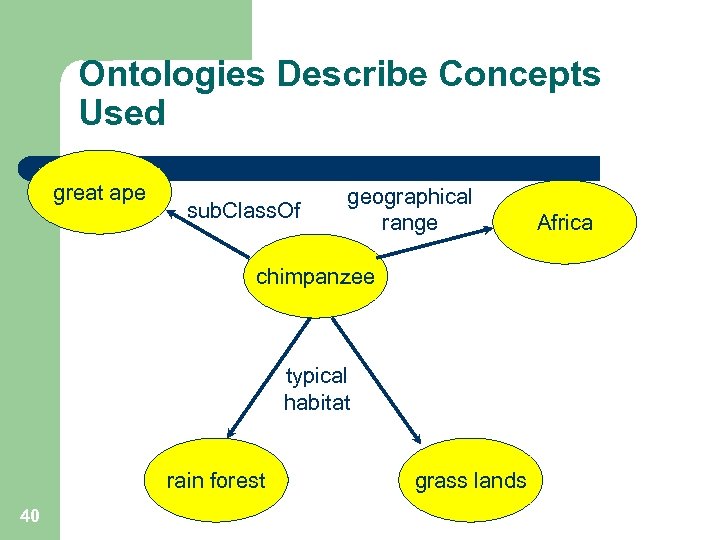Ontologies Describe Concepts Used great ape sub. Class. Of geographical range chimpanzee typical habitat rain forest 40 grass lands Africa
Logic versus Ontologies l The previous example involves knowledge typically found in ontologies – – l Logic is more general than ontologies – 41 Logic can be used to uncover ontological knowledge that is implicitly given It can also help uncover unexpected relationships and inconsistencies It can also be used by intelligent agents for making decisions and selecting courses of action Lugano course, November 2009 Knowledge Representation
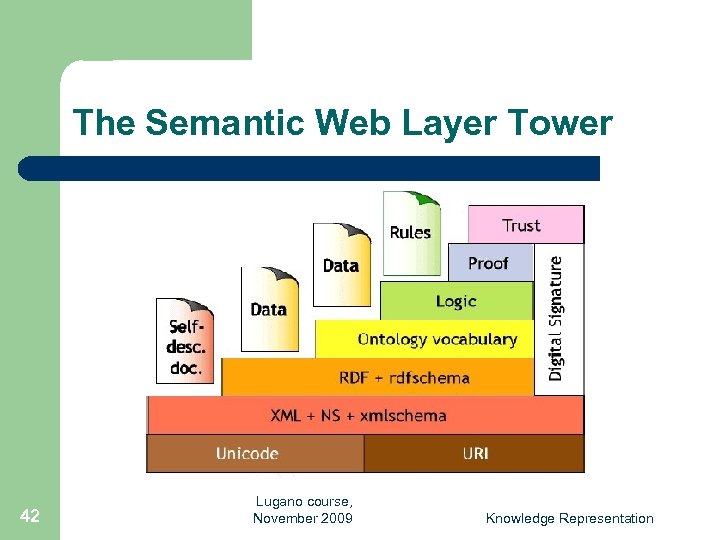The Semantic Web Layer Tower 42 Lugano course, November 2009 Knowledge Representation
Semantic Web Layers l XML layer – l RDF layer – – l RDF basic data model for facts RDF Schema simple ontology language Ontology layer – – 43 Syntactic basis More expressive languages than RDF Schema Current Web standard: OWL Lugano course, November 2009 Knowledge Representation
Semantic Web Layers (2) l Logic layer – – l Proof layer – l Proof generation, exchange, validation Trust layer – – 44 enhance ontology languages further application-specific declarative knowledge Digital signatures recommendations, rating agencies …. Lugano course, November 2009 Knowledge Representation
The Semantic Web l l 45 The Semantic Web vision RDF OWL Rules Lugano course, November 2009 Knowledge Representation
Basic Ideas of RDF l Basic building block: object-attribute-value triple – – l RDF has been given a syntax in XML – – 46 It is called a statement Sentence about Billington is such a statement This syntax inherits the benefits of XML Other syntactic representations of RDF possible Lugano course, November 2009 Knowledge Representation
Basic Ideas of RDF (2) l The fundamental concepts of RDF are: – – – 47 resources properties statements Lugano course, November 2009 Knowledge Representation
Resources l We can think of a resource as an object, a “thing” we want to talk about – l l Every resource has a URI, a Universal Resource Identifier A URI can be – – 48 E. g. authors, books, publishers, places, people, hotels a URL (Web address) or some other kind of unique identifier Lugano course, November 2009 Knowledge Representation
Properties l l Properties are a special kind of resources They describe relations between resources – l l Properties are also identified by URIs Advantages of using URIs: – – 49 E. g. “written by”, “age”, “title”, etc. Α global, worldwide, unique naming scheme Reduces the homonym problem of distributed data representation Lugano course, November 2009 Knowledge Representation
Statements l l Statements assert the properties of resources A statement is an object-attribute-value triple – l Values can be resources or literals – 50 It consists of a resource, a property, and a value Literals are atomic values (strings) Lugano course, November 2009 Knowledge Representation
Three Views of a Statement A triple l A piece of a graph l A piece of XML code Thus an RDF document can be viewed as: l A set of triples l A graph (semantic net) l An XML document l 51 Lugano course, November 2009 Knowledge Representation
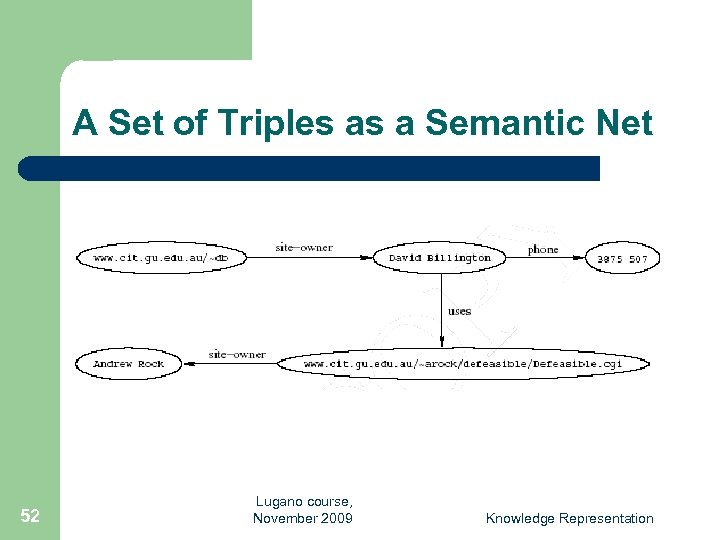A Set of Triples as a Semantic Net 52 Lugano course, November 2009 Knowledge Representation
Basic Ideas of RDF Schema l RDF is a universal language that lets users describe resources in their own vocabularies – l The user can do so in RDF Schema using: – – – 53 RDF does not assume, nor does it define semantics of any particular application domain Classes and Properties Class Hierarchies and Inheritance Property Hierarchies Lugano course, November 2009 Knowledge Representation
Classes and their Instances l We must distinguish between – – l l 54 Concrete “things” (individual objects) in the domain: Discrete Maths, David Billington etc. Sets of individuals sharing properties called classes: lecturers, students, courses etc. Individual objects that belong to a class are referred to as instances of that class The relationship between instances and classes in RDF is through rdf: type Lugano course, November 2009 Knowledge Representation
Why Classes are Useful l Impose restrictions on what can be stated in an RDF document using the schema – – – 55 As in programming languages E. g. A+1, where A is an array Disallow nonsense from being stated Lugano course, November 2009 Knowledge Representation
Nonsensical Statements disallowed through the Use of Classes l Discrete Maths is taught by Concrete Maths – – l Room MZH 5760 is taught by David Billington – – 56 We want courses to be taught by lecturers only Restriction on values of the property “is taught by” (range restriction) Only courses can be taught This imposes a restriction on the objects to which the property can be applied (domain restriction) Lugano course, November 2009 Knowledge Representation
Class Hierarchies l Classes can be organised in hierarchies – – l l 57 A is a subclass of B if every instance of A is also an instance of B Then B is a superclass of A A subclass graph need not be a tree A class may have multiple superclasses Lugano course, November 2009 Knowledge Representation
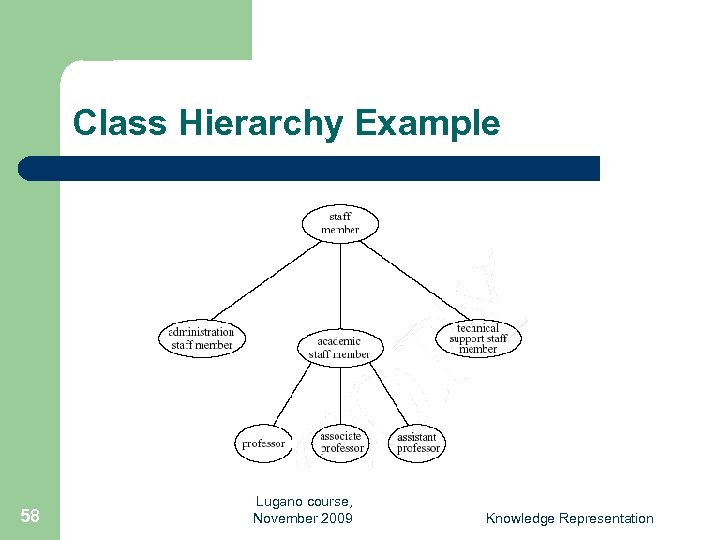Class Hierarchy Example 58 Lugano course, November 2009 Knowledge Representation
Inheritance in Class Hierarchies l l Range restriction: Courses must be taught by academic staff members only Michael Maher is a professor He inherits the ability to teach from the class of academic staff members This is done in RDF Schema by fixing the semantics of “is a subclass of” – 59 It is not up to an application (RDF processing software) to interpret “is a subclass of” Lugano course, November 2009 Knowledge Representation
Property Hierarchies l Hierarchical relationships for properties – – l The converse is not necessarily true – – l 60 E. g. , “is taught by” is a subproperty of “involves” If a course C is taught by an academic staff member A, then C also involves Α E. g. , A may be the teacher of the course C, or a tutor who marks student homework but does not teach C P is a subproperty of Q, if Q(x, y) is true whenever P(x, y) is true Lugano course, November 2009 Knowledge Representation
Summary of Basic RDF Functionalities l l l 61 Metadata statements Instances and classes Binary properties Class hierarchies Property hierarchies Domain and range restrictions Lugano course, November 2009 Knowledge Representation
The Semantic Web l l 62 The Semantic Web vision RDF OWL Rules Lugano course, November 2009 Knowledge Representation
Reasoning About Knowledge in Ontology Languages l Class membership – l Equivalence of classes – 63 If x is an instance of a class C, and C is a subclass of D, then we can infer that x is an instance of D If class A is equivalent to class B, and class B is equivalent to class C, then A is equivalent to C, too Lugano course, November 2009 Knowledge Representation
Reasoning About Knowledge in Ontology Languages (2) l Consistency – – l Classification – 64 X instance of classes A and B, but A and B are disjoint This is an indication of an error in the ontology Certain property-value pairs are a sufficient condition for membership in a class A; if an individual x satisfies such conditions, we can conclude that x must be an instance of A Lugano course, November 2009 Knowledge Representation
Uses for Reasoning l Reasoning support is important for – – – l Checks like the preceding ones are valuable for – – 65 checking the consistency of the ontology and the knowledge checking for unintended relationships between classes automatically classifying instances in classes designing large ontologies, where multiple authors are involved integrating and sharing ontologies from various sources Lugano course, November 2009 Knowledge Representation
Reasoning Support for OWL l l Semantics is a prerequisite for reasoning support Formal semantics and reasoning support are usually provided by – – l l 66 mapping an ontology language to a known logical formalism using automated reasoners that already exist for those formalisms OWL is (partially) mapped on a description logic, and makes use of reasoners such as Fa. CT and RACER Description logics are a subset of predicate logic for which efficient reasoning support is possible Lugano course, November 2009 Knowledge Representation
Limitations of the Expressive Power of RDF Schema l Local scope of properties – – – 67 rdfs: range defines the range of a property (e. g. eats) for all classes In RDF Schema we cannot declare range restrictions that apply to some classes only E. g. we cannot say that cows eat only plants, while other animals may eat meat, too Lugano course, November 2009 Knowledge Representation
Limitations of the Expressive Power of RDF Schema (2) l Disjointness of classes – l Boolean combinations of classes – – 68 Sometimes we wish to say that classes are disjoint (e. g. male and female) Sometimes we wish to build new classes by combining other classes using union, intersection, and complement E. g. person is the disjoint union of the classes male and female Lugano course, November 2009 Knowledge Representation
Limitations of the Expressive Power of RDF Schema (3) l Cardinality restrictions – l Special characteristics of properties – – – 69 E. g. a person has exactly two parents, a course is taught by at least one lecturer Transitive property (like “greater than”) Unique property (like “is mother of”) A property is the inverse of another property (like “eats” and “is eaten by”) Lugano course, November 2009 Knowledge Representation
Three Species of OWL l W 3 C’s. Web Ontology Working Group defined OWL as three different sublanguages: – – – l 70 OWL Full OWL DL OWL Lite Recent modifications have led to OWL 2 with new sublanguages Lugano course, November 2009 Knowledge Representation
Summary of Selected Key OWL Functionalities l l l 71 Equality of classes and properties Important property characteristics: transitive, functional, inverse Union, intersection and compement of classes All. Values. From(P, D): All values of statements with property P must be from class D Cardinality constraints Lugano course, November 2009 Knowledge Representation
The Semantic Web l l 72 The Semantic Web vision RDF OWL Rules Lugano course, November 2009 Knowledge Representation
Orthogonal Expressivity Why consider rules? – Well established technology, used in the business world, natural for many apps Orthogonal expressivity: – – 73 OWL is based on Description Logic Horn logic is orthogonal w. r. t. DL Lugano course, November 2009 Knowledge Representation
What OWL Cannot Express It is impossible to define classes whose instances are related to another anonymous individual via different property paths. l E. g. “Home workers are those who live and work in the same location. l Easily expressed in Horn logic: home. Worker(X) : work(X, Y), live(X, Z), loc(Y, W), loc(Z, W). 74 Lugano course, November 2009 Knowledge Representation
What Horn Logic Cannot Express 1. Existential quantification – 2. Disjunction / union – 3. E. g. Persons are men or women. Negation / complement – 75 E. g. All persons have a father. E. g. Men and women are disjoint. Lugano course, November 2009 Knowledge Representation
RDFS and Horn Logic Statement(a, P, b) type(a, C) C sub. Class. Of D P sub. Porperty. Of Q domain(P, C) range(P, C) 76 Lugano course, November 2009 P(a, b) C(a) C(X) D(X) P(X, Y) Q(X, Y) P(X, Y) C(X) P(X, Y) C(Y) Knowledge Representation
OWL in Horn Logic C same. Class. As D C(X) D(X) C(X) P same. Property. As Q P(X, Y) Q(X, Y) P(X, Y) 77 Lugano course, November 2009 Knowledge Representation
OWL in Horn Logic (2) transitive. Property(P) P(X, Y), P(Y, Z) P(X, Z) inverse. Property(P, Q) Q(X, Y) P(Y, X) P(X, Y) Q(Y, X) functional. Property(P) P(X, Y), P(X, Z) Y=Z 78 Lugano course, November 2009 Knowledge Representation
OWL in Horn Logic (3) (C 1 C 2) sub. Class. Of D C 1(X), C 2(X) D(X) C sub. Class. Of (D 1 D 2) C(X) D 1(X) C(X) D 2(X) 79 Lugano course, November 2009 Knowledge Representation
OWL in Horn Logic (4) (C 1 C 2) sub. Class. Of D C 1(X) D(X) C 2(X) D(X) C sub. Class. Of (D 1 D 2) Translation not possible! 80 Lugano course, November 2009 Knowledge Representation
OWL in Horn Logic (5) C sub. Class. Of All. Values. From(P, D) C(X), P(X, Y) D(Y) All. Values. From(P, D) sub. Class. Of C Translation not possible! 81 Lugano course, November 2009 Knowledge Representation
OWL in Horn Logic (6) l l l 82 Min. Cardinality cannot be translated due to existential quantification Max. Cardinality 1 may be translated if equality is allowed Complement cannot be translated, in general Lugano course, November 2009 Knowledge Representation
Part III: Defeasible Reasoning 83 Lugano course, November 2009 Knowledge Representation
Defeasible Reasoning l l l 84 Nonmonotonic Reasoning: Motivation Defeasible Logic: Basic Ideas Defeasible Logic: Properties Lugano course, November 2009 Knowledge Representation
New Information l What time do I arrive in Lugano? – l New information: My flight is delayed by an hour – l 6: 30 pm (by bus from Malpensa) New answer: 8: 30 pm! New information has led to the retraction of my previous reply: nonmonotonic behaviour 85 Lugano course, November 2009 Knowledge Representation
Incomplete Information l Why did it happen? l Actually because I made assumptions (no delay) that turned out to be wrong l I made these assumptions because: – I could not have known in advance: certain information is incomplete – 86 Otherwise I would be seen to be strange Lugano course, November 2009 Knowledge Representation
Incomplete Information on the Web l Business rules deal with incomplete information: – l In Web applications other players may not be able or willing to provide information. – – 87 In the absence of information some assumptions have to be made which lead to conclusions not supported by classical predicate logic. Communication problems Privacy or security concerns Lugano course, November 2009 Knowledge Representation
Inconsistent Information l Classical logics “collapse” in the face of inconsistencies – l But inconsistencies do happen in real settings – l 88 Everything can be derived Common when integrating knowledge from various Web sources Nonmonotonic reasoning is inconsistency tolerant reasoning Lugano course, November 2009 Knowledge Representation
Rules with Exceptions l l l Natural representation for policies and business rules. Priority information is often implicitly or explicitly available to resolve conflicts among rules. Potential applications – – – 89 Security policies Business rules Personalization Brokering Bargaining, automated agent negotiations Lugano course, November 2009 Knowledge Representation
Defeasible Reasoning l l l 90 Nonmonotonic Reasoning: Motivation Defeasible Logic: Basic Ideas Defeasible Logic: Properties Lugano course, November 2009 Knowledge Representation
Defeasible Logics l l Rule-based, without disjunction. Classical negation is used in the heads and bodies of rules – l l Rules may support conflicting conclusions. Skeptical: Conflicting rules do not fire. – l 91 Negation-as-failure is not used but can be emulated Consistency is preserved. Priorities on rules may be used to resolve some conflicts among rules. Lugano course, November 2009 Knowledge Representation
Example 1 R 1: a a provable? 92 Lugano course, November 2009 Knowledge Representation
Example 1 R 1: a +a Yes (of course) 93 Lugano course, November 2009 Knowledge Representation
Example 2 R 1: a R 2: a a provable? 94 Lugano course, November 2009 Knowledge Representation
Example 2 R 1: a R 2: a -a - a No! (sceptical) 95 Lugano course, November 2009 Knowledge Representation
Example 3 R 1: a R 2: a R 1>R 2 a provable? 96 Lugano course, November 2009 Knowledge Representation
Example 3 R 1: a R 2: a R 1>R 2 +a - a Yes! 97 Lugano course, November 2009 Knowledge Representation
Example 4 R 1: a b R 2: b R 1>R 2 b provable? 98 Lugano course, November 2009 Knowledge Representation
Example 4 R 1: a b R 2: b R 1>R 2 -a + b -b No, quite the opposite. 99 Lugano course, November 2009 Knowledge Representation
Example 5 R 1: a R 2: a R 3: a b R 4: a b b provable? 100 Lugano course, November 2009 Knowledge Representation
Example 5 R 1: a R 2: a R 3: a b R 4: a b -a - a -b No (no “floating conclusions”) 101 Lugano course, November 2009 Knowledge Representation
Example 6 R 1: a R 2: a R 3: a b R 4: b b provable? 102 Lugano course, November 2009 Knowledge Representation
Example 6 R 1: a R 2: a R 3: a b R 4: b -a -b + b Yes (no propagation of ambiguity) 103 Lugano course, November 2009 Knowledge Representation
Example 7 R 1: a R 2: a R 3: a b R 4: a b R 1>R 2 R 4>R 3 b or b provable? 104 Lugano course, November 2009 Knowledge Representation
Example 7 R 1: a R 2: a R 3: a b R 4: a b R 1>R 2 R 4>R 3 +a - b +b b (sequence of conflict resolution important) 105 Lugano course, November 2009 Knowledge Representation
Example 8 R 1: a e R 2: b e R 3: c e R 4: d e abcd R 1>R 3 e provable? 106 Lugano course, November 2009 Knowledge Representation
Example 8 R 1: a e R 2: b e R 3: c e R 4: d e abcd R 1>R 3 No (not inferior attack by R 4) 107 Lugano course, November 2009 +a +b +c +d -e - e Knowledge Representation
Example 9 (Team Defeat) R 1: a e R 2: b e R 3: c e R 4: d e abcd R 1>R 3 R 2>R 4 108 +a +b +c +d +e Lugano course, November 2009 Knowledge Representation
Defeasible Reasoning l l l 109 Nonmonotonic Reasoning: Motivation Defeasible Logic: Basic Ideas Defeasible Logic: Properties Lugano course, November 2009 Knowledge Representation
Important Properties l l l 110 Consistency: +A and + A cannot be both derived, unless they are already known as certain knowledge (facts) Coherence: +A and –A cannot be derived from the same knowledge base. Complexity: Defeasible logic has linear complexity. Lugano course, November 2009 Knowledge Representation
Semantic Characterization l l l 111 Defeasible logic is defined as a proof theory. A more abstract characterization is desirable. Argumentation semantics: More abstract definition of meaning in terms of arguments (reasoning chains) and their mutual interactions. Proof theory is sound and complete w. r. t. this semantics Lugano course, November 2009 Knowledge Representation
Connection to Logic Programming l Based on the translation of defeasible theories into logic programs through the wellstudied meta-program of – Antoniou G. , Billington D. , Governatori G. , Maher M. J, "A Flexible Framework for Defeasible Logics", Proc. AAAI/IAAI 2000, AAAI/MIT Press, pp. 405 -410. 112 Lugano course, November 2009 Knowledge Representation
The Meta-Program definitely(X) : - fact(X). definitely(X) : strict(R, X, [Y 1, . . . , Yn]), definitely(Y 1), . . . , definitely(Yn). defeasibly(X) : - definitely(X). defeasibly(X) : not definitely( X), supportive_rule(R, X, [Y 1, . . . , Yn]), defeasibly(Y 1), . . . , defeasibly(Yn), not overruled(R, X). 113 Lugano course, November 2009 Knowledge Representation
The Meta-Program (2) overruled(R, X) : rule(S, X, [U 1, . . . , Un]), defeasibly(U 1), . . . , defeasibly(Un), not defeated(S, X). defeated(S, X) : sup(T, S), supportive rule(T, X, [V 1, . . . , Vn]), defeasibly(V 1), . . . , defeasibly(Vn). 114 Lugano course, November 2009 Knowledge Representation
The Meta-Program (3) supportive_rule(Name, Head, Body): strict(Name, Head, Body). supportive_rule(Name, Head, Body): defeasible(Name, Head, Body). rule(Name, Head, Body): supportive_rule(Name, Head, Body): defeater(Name, Head, Body). 115 Lugano course, November 2009 Knowledge Representation
Part IV: Applications of Defeasible Reasoning 116 Lugano course, November 2009 Knowledge Representation
Applications l l l 117 Semantic brokering Electronic auctions Pervasive computing / ambient intelligence Lugano course, November 2009 Knowledge Representation
Motivation l 1 st generation e-commerce (present) – – – l 2 nd generation e-commerce (future) – 118 Buyers and sellers are humans Catalogue of well-defined commodities Fixed price purchases by means of credit card transaction Buyers and sellers are software agents Lugano course, November 2009 Knowledge Representation
Background Theory – Brokering l l 119 Brokering or matchmaking: process that requires a host to take a query and to return all advertisements which satisfy the requirements specified in the query – Advertisements – Preferences – Brokering Engine Brokering engine uses a specific technique and performs the matching of preferences with advertisements Lugano course, November 2009 Knowledge Representation
Suitability of Defeasible Logic l l l 120 Formal language with well-understood meaning, a proof theory, model semantics, and argumentation semantics It is predictable , explainable and has linear complexity Sceptical formalism. It does not support contradictory conclusions Lugano course, November 2009 Knowledge Representation
Suitability of Defeasible Logic (2) l Natural representation of important features: – – 121 Rules with exceptions Priorities for expressing user preferences Lugano course, November 2009 Knowledge Representation
An Apartment Renting Example l l 122 Apartments and their properties are the advertisements The renter’s requirements and preferences are expressed in defeasible logic Lugano course, November 2009 Knowledge Representation
User Requirements & Preferences 1. Carlos is looking for an apartment of at least 45 m 2 with at least 2 bedrooms. If it is on the 3 rd floor or higher, the house must have an elevator. Also, pet animals must be allowed. 2. Carlos is willing to pay $300 for a centrally located 45 m 2 apartment, and $250 for a similar flat in the suburbs. In addition, he is willing to pay an extra $5 per m 2 for a larger apartment, and $2 per m 2 for a garden. 3. He is unable to pay more than $400 in total. If given the choice, he would go for the cheapest option. His 2 nd priority is the presence of a garden; lowest priority is additional space. 123 Lugano course, November 2009 Knowledge Representation
Predicates Used in Formalization l l l l 124 size(x, y), where y is the size of apartment x (in m 2) bedrooms(x, y), where apartment x has y bedrooms price(x, y), where y is the price for x floor(x, y), where apartment x is on the y-th floor garden. Size(x, y), where apartment x has a garden of size y lift(x), meaning that there is an elevator in the house of x pets(x), meaning that pets are allowed in x central(x), meaning that x is centrally located Lugano course, November 2009 Knowledge Representation
Predicates Used (2) l l 125 acceptable(x), meaning that flat x satisfies Carlos’s requirements offer(x, y), meaning that Carlos is willing to pay $ y for flat x Lugano course, November 2009 Knowledge Representation
Formalization of Requirements r 1: => acceptable(X) r 2: bedrooms(X, Y), Y < 2 => ¬acceptable(X) r 3: size(X, Y), Y < 45 => ¬acceptable(X) r 4: ¬pets(X) => ¬acceptable(X) r 5: floor(X, Y), Y > 2, ¬lift(X) => ¬acceptable(X) r 6: price(X, Y), Y > 400 => ¬acceptable(X) r 2 > r 1, r 3 > r 1, r 4 > r 1, r 5 > r 1, r 6 > r 1 126 Lugano course, November 2009 Knowledge Representation
Formalization of Requirements (2) r 7: size(X, Y), Y ≥ 45, garden(X, Z), central(X) => offer(X, 300 + 2 Z + 5(Y− 45)) r 8: size(X, Y), Y ≥ 45, garden(X, Z), ¬central(X) => offer(X, 250 + 2 Z + 5(Y− 45)) r 9: offer(X, Y), price(X, Z), Y < Z => ¬acceptable(X) r 9 > r 1 127 Lugano course, November 2009 Knowledge Representation
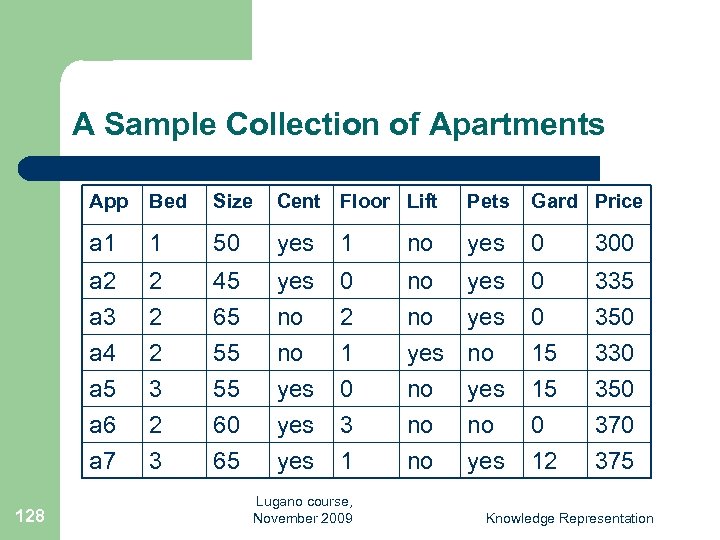A Sample Collection of Apartments App Size Cent Floor Lift Pets Gard Price a 1 1 50 yes 1 no yes 0 300 a 2 a 3 2 2 45 65 yes no 0 2 no no yes 0 0 335 350 a 4 a 5 a 6 a 7 128 Bed 2 3 55 55 60 65 no yes yes 1 0 3 1 yes no no yes 15 15 0 12 330 350 375 Lugano course, November 2009 Knowledge Representation
Results of User Requirements l l 129 Apartment a 1 is not acceptable because it has one bedroom only (rule r 2). Apartments a 4 and a 6 are unacceptable because pets are not allowed (rule r 4). Apartment a 2 is unacceptable because it costs more than the $300 Carlos is willing to pay (rules r 7 & r 9). The rest, a 3, a 5 and a 7, are acceptable. Lugano course, November 2009 Knowledge Representation
Formalization of User Preferences r 10: acceptable(X), price(X, Z), not(acceptable(Y), Y X, price(Y, W), W < Z) => cheapest(X) r 11: cheapest(X), garden. Size(X, Z), not(cheapest(Y), Y X, garden. Size(Y, W), W < Z) => largest. Garden(X) r 12: largest. Garden(X), size(X, Z), not(largest. Garden(Y), Y X, size(Y, W), W < Z) => rent(X) 130 Lugano course, November 2009 Knowledge Representation
Results of User Preferences l l 131 Apartments a 3 and a 5 are the cheapest acceptable apartments (rule r 10) a 5 is selected because it has larger garden than a 3 (rules r 11 and r 12) Lugano course, November 2009 Knowledge Representation
Applications l l l 132 Semantic brokering Electronic auctions Pervasive computing / ambient intelligence Lugano course, November 2009 Knowledge Representation
Auction Strategies English Auction: l One of the most popular one-to-many negotiation mechanisms l Simplest form: multi-party single-issue negotiation l Popular in Internet trading 133 Lugano course, November 2009 Knowledge Representation
English Auction Principles l l Seller sets reservation price, which may or may not be announced to the bidders Seller sets timing constraint, – l 134 firm deadline, as maximum duration between two successive bids, or both Potential buyers then issue increasingly higher bids, with increment threshold Lugano course, November 2009 Knowledge Representation
English Auction Principles (2) l Auction stops when the timing constraint is violated – l l 135 i. e. either the deadline is reached, or no bid registered for longer than the established maximum duration. The last bidder then buys the item at the price of the last bid If no bid above reservation price, the item is not sold Lugano course, November 2009 Knowledge Representation
Auction Broker l l l 136 Standard in online trading communities Registers the parameters of the auction Publishes them Processes incoming bids Continuously makes accessible the auction's status Lugano course, November 2009 Knowledge Representation
A Sample Bidder Strategy Mark wishes to participate in the auction of an item. He doesn't know exactly how much the item is worth, but he thinks that its value lies somewhere within two bounds L and U. He is keen not to over-value the item, so he decides to assume at the beginning of the auction that the item is worth L, and to eventually increase his valuation whenever one of the following two situations occurs: (a) at least 3 bids above his current valuation have been registered, or (b) somebody has bid more than 20% of his current valuation. 137 Lugano course, November 2009 Knowledge Representation
A Sample Bidder Strategy (2) As soon as one of these conditions is met, Mark will raise his valuation by the minimum possible amount that allows him to stay in the auction. However, he will never accept to valuate the item above U. As it is usual in the case of English auctions, Mark will start by bidding some minimum amount (i. e. the reservation price), and if needed, he will subsequently overbid the other participants' bids by the minimum increment, as long as the resulting bid is less than his current valuation. In the eventuality where the auction's deadline is too close and that he does not hold the current highest bid, he will bid his current valuation instead of just overbidding by the minimum increment. 138 Lugano course, November 2009 Knowledge Representation
Predicates & Functions for Auction Description l l l 139 min_increment denotes the minimum mount by which the bidders are allowed to overbid initial_bid denotes the minimum amount of the first acceptable bid. (reservation price may be higher, but unknown to bidders) time_remaining(T) provides the time remaining before the end of the auction highest_quote(N) provides the current highest bid quotes_above(X, N) holds if N bids above amount X have been registered. Lugano course, November 2009 Knowledge Representation
Predicates & Functions for Bidding Strategy l l l 140 time_threshold is the duration to the deadline, below which Mark estimates that he should bid his valuation instead of just overbidding by the minimum increment significant_bidders is the number of bidders that should bid above Mark's current valuation before he considers raising it significant_increment is the amount (expressed as a percentage), that another bidder should bid above Mark's current valuation before he considers raising it (in working example it is 0, 2) Lugano course, November 2009 Knowledge Representation
Predicates & Functions for Bidding Strategy (2) l max_valuation is self-explainable l submit_bid(X) states that a bid of amount X should be submitted valuation(X) gives the current valuation while pre_valuation(X) gives the valuation that was valid at the end of the previous activation of the reasoning module my_bid(X) gives the amount of the last accepted bid issued by the bidder. At the beginning of the auction my_bid(0) holds l l 141 Lugano course, November 2009 Knowledge Representation
Formalization of Bidding Strategy r 1: my_bid(X), highest_quote(Y), valuation(Z), X < Y, Y + min_increment < Z, time_remaining(T), T > time_threshold submit_bid(Y + min_increment) If there is enough time remaining and the agent's current bid is not the highest one, it should be increased by the minimum increment, provided that the current valuation allows so. 142 Lugano course, November 2009 Knowledge Representation
Formalization of Bidding Strategy (2) r 2: my_bid(X), highest_quote(Y), valuation(Z), X < Y, Y + min_increment < Z, time_remaining(T), T time_threshold submit_bid(Z) If the deadline is close and the bidder does not hold the item, a bid of the amount of the current valuation should be submitted immediately. 143 Lugano course, November 2009 Knowledge Representation
Formalization of Bidding Strategy (3) r 3: pre_valuation(X) r 4: pre_valuation(X), quotes_above(X, N), N significant_bidders, highest_quote(Y) valuation(Y + min_increment) r 5: pre_valuation(X), highest_quote(Y), Y > (1 + significant_increment) X valuation(Y + min_increment) r 6: Y > max_valuation ~> valuation(Y) r 4 > r 3, r 5 > r 3 144 Lugano course, November 2009 Knowledge Representation
Formalization of Bidding Strategy (4) Conflicting literals: l C(submit_bid(x)) = { submit_bid(y) | y x } l C(new_valuation(x)) = { new_valuation(y) | y x } 145 Lugano course, November 2009 Knowledge Representation
Formalization of Bidding Strategy (5) l Rules r 3 through r 6 allow to derive the valuation – – 146 r 4 and r 5 model the two conditions under which the valuation should be raised r 6 is a defeater modeling the fact that the bidder is under no circumstances willing to valuate the item above a given amount. Lugano course, November 2009 Knowledge Representation
Modularity of the Formalization Suppose user wants to modify the strategy l “raise the valuation if the reservation price has not been met and the highest bid is above my current valuation” Just add the rule: r 7: reservation_not_met, valuation(X), highest_quote(Y), Y > X valuation(Y + min_increment) r 7 > r 3 147 Lugano course, November 2009 Knowledge Representation
Modularity of the Formalization (2) We don’t have to worry whether the reservation price is greater than the bidder’s maximum valuation or not. 148 Lugano course, November 2009 Knowledge Representation
Applications l l l 149 Semantic brokering Electronic auctions Pervasive computing / ambient intelligence Lugano course, November 2009 Knowledge Representation
Context in Ambient Intelligence l l 150 Aim of Am. I systems – right information to the right users, at the right time, in the right place, and on the right device l thorough knowledge and understanding of context Context in Ambient Intelligence – “. . any information that can be used to characterize the situation of an entity. An entity is a person, place or object that is considered relevant to the interaction between a user and application, including the user and application themselves. . ” [Dey and Abowd, 1999] Lugano course, November 2009 Knowledge Representation
Contextual Reasoning in Ambient Intelligence l l 151 Challenges – Imperfect nature of the available context information l Unknown, ambiguous, imprecise, erroneous – Special characteristics of ambient environments l Highly dynamic and open environments l Distributed context knowledge l Unreliable and restricted wireless communications Limitations of current Am. I systems – No formal model for reasoning with imperfect context – Centralized architectures → No support for distributed reasoning Lugano course, November 2009 Knowledge Representation
Motivating Am. I Scenario Dr. Amber is located in the ‘RA 201’ university classroom reading his e-mails on his laptop. It is Tuesday, the time is 7. 50 p. m. , and he has just finished with a lecture for course CS 566. His context-aware mobile phone receives an incoming call, but it is not in silent mode. Dr. Amber’s phone is configured to take decisions about whether it should ring in case of incoming calls based on its context and Dr. Amber’s preferences: –The phone should ring, unless it is in silent mode or Dr. Amber is busy with some important activity. –A lecture at the university is one such important activity. 152 Lugano course, November 2009 Knowledge Representation
Motivating Am. I Scenario class RA 201 no class activity 153 Lugano course, November 2009 one person detected Knowledge Representation
Scenario Characteristics l l 154 Assumptions – each agent aware of the type and quality of imported knowledge – each agent has some computing and reasoning capabilities – each agent willing to disclose part of its local knowledge Challenges – context is incomplete, imprecise, ambiguous – restricted computing capabilities – light communication load for making quick decisions Lugano course, November 2009 Knowledge Representation
Multi-Context Systems l l 155 Definition – Logical formalizations of distributed context theories connected through a set of mapping rules, which enable information flow between different contexts – Context: a logical theory that models local context knowledge Challenges – Heterogeneity of local context theories – Inconsistencies caused by the interaction of contexts through the mappings Lugano course, November 2009 Knowledge Representation
Global Inconsistency in MCS Context A k ¬k Context B 156 Context C Lugano course, November 2009 Knowledge Representation
Modeling the Am. I scenario – Local facts and rules r 11 l : r 12 l : r 13 l : r 14 l : – Phone (P 1) → incoming_call → normal_mode incoming_call, normal_mode, ¬important_activity → ring lecture → important_activity Mapping rules r 15 m : scheduled(CS 566)2, location(RA 201)3 lecture r 16 m : ¬class_activity 4 ¬ lecture – Preference relation T 1 = [P 3, P 4, P 2] 157 Lugano course, November 2009 Knowledge Representation
Modeling the Am. I scenario l l 158 Laptop (P 2) r 21 l : → day(Tuesday) r 22 l : → time(19. 50) r 23 l : day(Tuesday), time(X), 19. 00 < X < 20. 00 → scheduled(CS 566) Localization Service(P 3) r 41 l : → location(RA 201) Classroom Manager (P 4) r 41 l : → projector(off) r 42 m : → detected(X)5, X<2, projector(off) ¬ class_activity Person Detection Service(P 5) r 51 l : → detected(1) Lugano course, November 2009 Knowledge Representation
Future Work l l l 159 Overlapping vocabularies Access control & privacy mechanisms More applications in the Ambient Intelligence and Semantic Web domains – Run on small devices – Efficient reasoning is well-suited for real-world and realtime applications Lugano course, November 2009 Knowledge Representation
Part V: Summary 160 Lugano course, November 2009 Knowledge Representation
Summary l KR is about difficult problems that cannot be solved directly algorithmically – l KR is a multi-faceted area – l Always seeking a balance between expressive power and manageable computational complexity KR in contemporary ICT areas – – 161 Or offers advantages in terms of transparency, modularity and explanation Web Ambient Intelligence Lugano course, November 2009 Knowledge Representation
References The standard textbook on Knowledge Representation: l R. Brachman and H. Levesque. Knowledge Representation and Reasoning. Morgan Kaufmann 2004 The standard textbook on the Semantic Web: l G. Antoniou and F. van Harmelen. A Semantic Web Primer, 2 nd ed. MIT Press 2008 www. semanticwebprimer. org A useful page on the semantic web: l www. semanticweb. org 162 Lugano course, November 2009 Knowledge Representation
References (2) A textbook on nonmonotonic reasoning: l G. Antoniou. Nonmonotonic Reasoning. MIT Press 1997 A paper on defeasible logics: l 163 G. Antoniou, D. Billington, G. Governatori and M. Maher. Representation Results for Defeasible Logic. ACM Transactions on Computational Logic 2, 2 (2001): 255 -287 http: //eprint. uq. edu. au/archive/00002222/01/tocl. pdf Lugano course, November 2009 Knowledge Representation
References (3) A paper on brokering based on defeasible reasoning: l G. Antoniou, T. Skylogiannis, A. Bikakis, M. Doerr, N. Bassiliades. DR-BROKERING: A semantic brokering system. Knowledge-Based Systems 20(1): 61 -72 (2007) lpis. csd. auth. gr/publications/EEE 05 -a. pdf A paper on defeasible reasoning in ambient intelligence: l 164 A. Bikakis, G. Antoniou, P. Hasssapis. Strategies for Contextual Reasoning with Conflicts in Ambient Intelligence. Knowledge and Information Systems (forthcoming) Lugano course, November 2009 Knowledge Representation