Knowledge Engineering for Bayesian Networks Ann Nicholson School

Knowledge Engineering for Bayesian Networks Ann Nicholson School of Computer Science and Software Engineering Monash University 1

Overview l l Representing uncertainty Introduction to Bayesian Networks » Syntax, semantics, examples l l The knowledge engineering process Case Study: Intelligent Tutoring Summary of other BN research Open research questions 2

Sources of Uncertainty l l Ignorance Inexact observations Non-determinism AI representations » Probability theory » Dempster-Shafer » Fuzzy logic 3

Probability theory for representing uncertainty l Assigns a numerical degree of belief between 0 and 1 to facts » e. g. “it will rain today” is T/F. » P(“it will rain today”) = 0. 2 prior probability (unconditional) l Posterior probability (conditional) » P(“it wil rain today” | “rain is forecast”) = 0. 8 l Bayes’ Rule: P(H|E) = P(E|H) x P(H) P(E) 4

Bayesian networks l l l Directed acyclic graphs Nodes: random variables, » R: “it is raining”, discrete values T/F » T: temperature, cts or discrete variable » C: colour, discrete values {red, blue, green} Arcs indicate dependencies (can have causal interpretation) 5

Bayesian networks l Conditional Probability Distribution (CPD) – Associated with each variable – probability of each state given parent states “Jane has the flu” X Flu P(Flu=T) = 0. 05 Y Te P(Te=High|Flu=T) = 0. 4 P(Te=High|Flu=F) = 0. 01 Models causal relationship “Jane has a high temp” Models possible sensor error “Thermometer temp reading” Q Th P(Th=High|Te=H) = 0. 95 P(Th=High|Te=L) = 0. 1 6

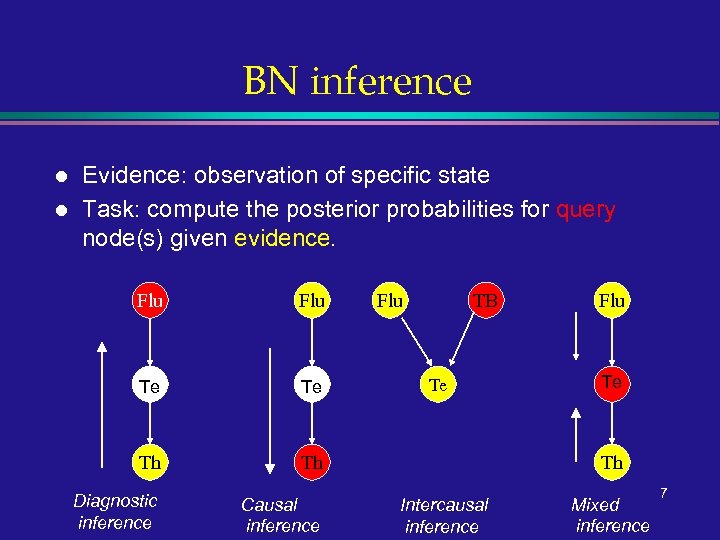
BN inference l l Evidence: observation of specific state Task: compute the posterior probabilities for query node(s) given evidence. Flu Y Te Th Th Diagnostic inference Causal inference Flu TB Te Flu Te Th Intercausal inference Mixed inference 7

BN software l l Commerical packages: Netica, Hugin, Analytica (all with demo versions) Free software: Smile, Genie, Java. Bayes, … http: //HTTP. CS. Berkeley. EDU/~murphyk/Bayes/bnsoft. html l Example running Netica software 8

Decision networks l Extension to basic BN for decision making » Decision nodes » Utility nodes l EU(Action) = p(o|Action, E) U(o) o » choose action with highest expect utility l Example 9

Elicitation from experts l Variables » important variables? values/states? l Structure » causal relationships? » dependencies/independencies? l Parameters (probabilities) » quantify relationships and interactions? l Preferences (utilities) 10

Expert Elicitation Process l l These stages are done iteratively Stops when further expert input is no longer cost effective Process is difficult and time consuming. Current BN tools » inference engine » GUI l BN EXPERT Domain EXPERT Next generation of BN tools? BN TOOLS 11

Knowledge discovery l There is much interest in automated methods for learning BNS from data » parameters, structure (causal discovery) l Computationally complex problem, so current methods have practical limitations » e. g. limit number of states, require variable ordering constraints, do not specify all arc directions l Evaluation methods 12

The knowledge engineering process 1. Building the BN » variables, structure, parameters, preferences » combination of expert elicitation and knowledge discovery 2. Validation/Evaluation » case-based, sensitivity analysis, accuracy testing 3. Field Testing » alpha/beta testing, acceptance testing 4. Industrial Use » collection of statistics 5. Refinement » Updating procedures, regression testing 13

Case Study: Intelligent tutoring l l Tutoring domain: primary and secondary school students’ misconceptions about decimals Based on Decimal Comparison Test (DCT) » student asked to choose the larger of pairs of decimals » different types of pairs reveal different misconceptions l l ITS System involves computer games involving decimals This research also looks at a combination of expert elicitation and automated methods (UAI 2001) 14

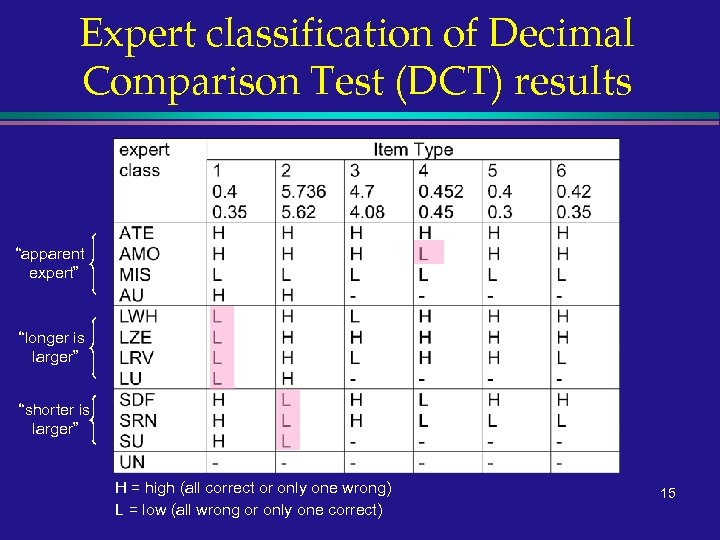
Expert classification of Decimal Comparison Test (DCT) results “apparent expert” “longer is larger” “shorter is larger” H = high (all correct or only one wrong) L = low (all wrong or only one correct) 15

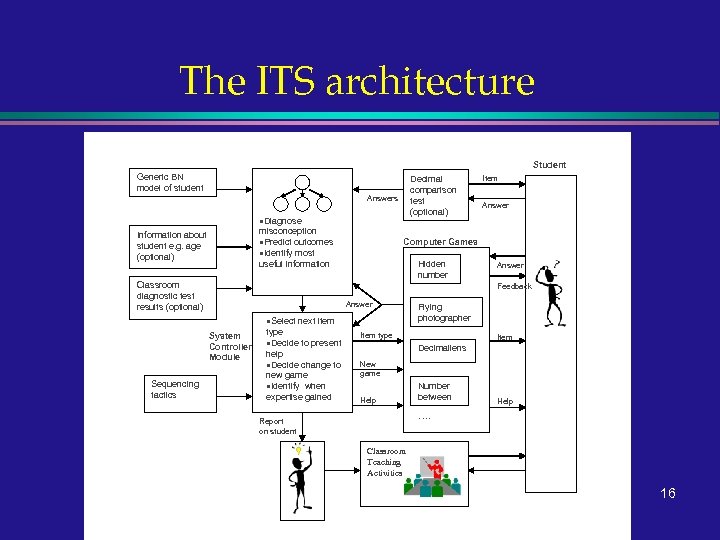
The ITS architecture Adaptive Bayesian Network Inputs Student Generic BN model of student Decimal comparison test (optional) Answers ·Diagnose misconception ·Predict outcomes ·Identify most useful information Information about student e. g. age (optional) Classroom diagnostic test results (optional) Answer Computer Games Hidden number Answer Feedback Answer ·Select next item System Controller Module Sequencing tactics Item type ·Decide to present help ·Decide change to new game ·Identify when expertise gained Flying photographer Item type Item Decimaliens New game Help Number between Help …. Report on student Classroom Teaching Activities 16 Teacher

Expert Elicitation l Variables » two classification nodes: fine and coarse (mut. ex. ) » item types: (i) H/M/L (ii) 0 -N l Structure » arcs from classification to item type » item types independent given classification l Parameters » careless mistake (3 different values) » expert ignorance: - in table (uniform distribution) 17

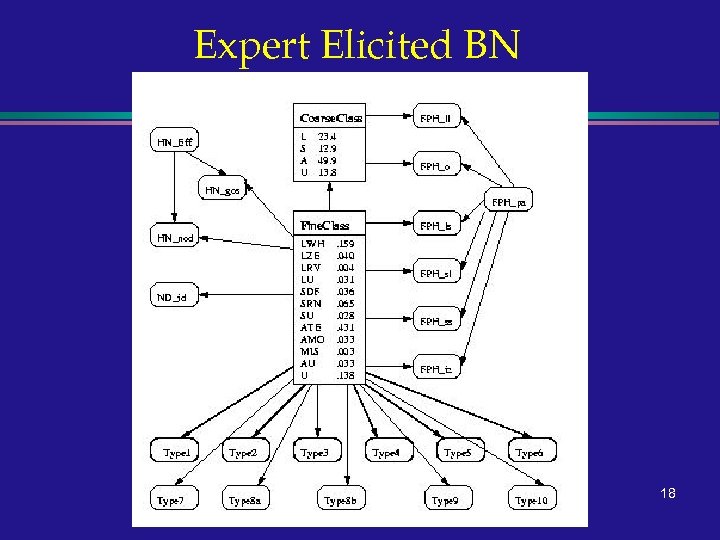
Expert Elicited BN 18

Evaluation process l Case-based evaluation » experts checked individual cases » sometimes, if prior was low, ‘true’ classification did not have highest posterior (but usually had biggest change in ratio) l Adaptiveness evaluation » priors changes after each set of evidence l Comparison evaluation » Differences in classification between BN and expert rule » Differences in predictions between different BNs 19

Comparison evaluation l l l Development of measure: same classification, desirable and undesirable re-classification Use item type predictions Investigation of effect of item type granularity and probability of careless mistake 20

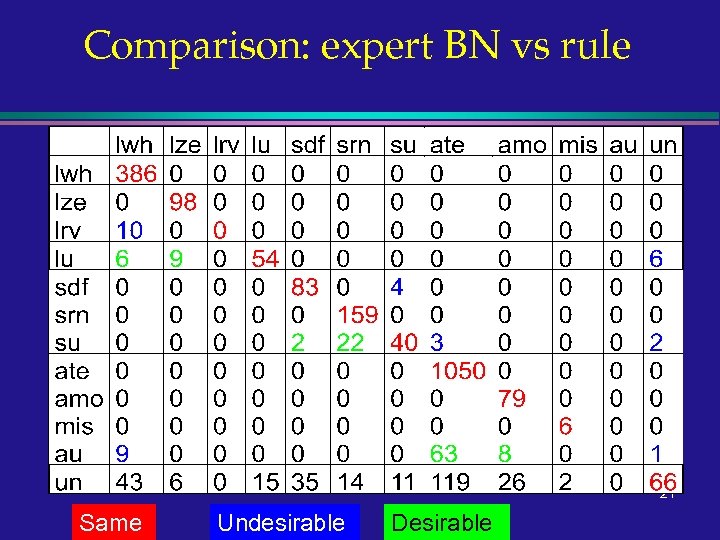
Comparison: expert BN vs rule 21 Same Undesirable Desirable

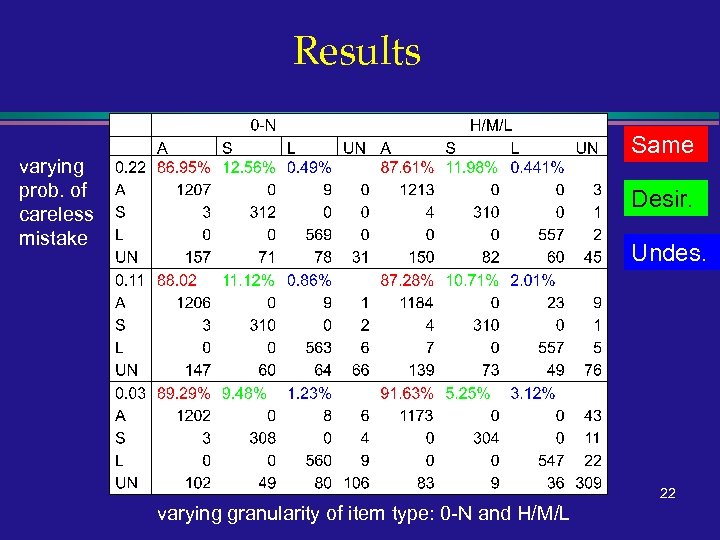
Results Same varying prob. of careless mistake Desir. Undes. 22 varying granularity of item type: 0 -N and H/M/L

Investigation by Automated methods l l l Classification (using SNOB program, based on MML) Parameters Structure (using Ca. MML) 23

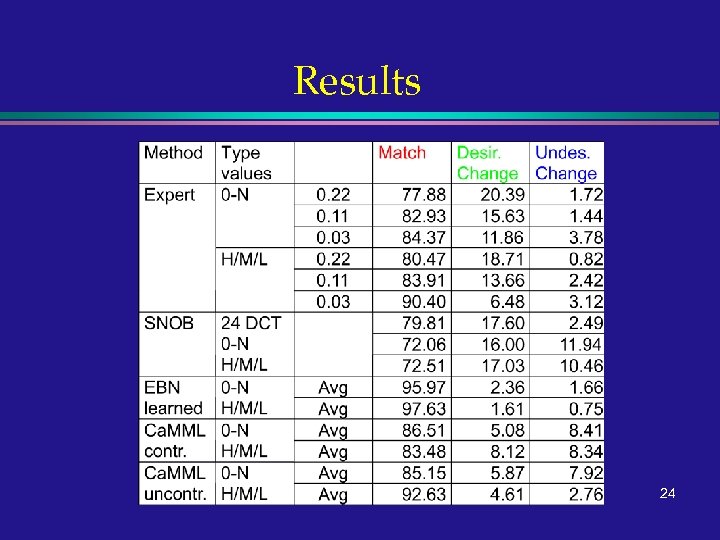
Results 24

Another Case Study: Seabreeze prediction l l l 2000 Honours project, joint with Bureau of Meteorology (with Russell Kennett and Kevin Korb, PAKDD’ 2001 paper, TR) BN network built based on existing simple expert rule Several years data available for Sydney seabreezes Ca. MML (Wallace and Korb, 1999) and Tetrad-II (Spirtes et al. 1993) programs used to learn BNs from data Comparative analysis showed automated methods gave improved predictions. 25

Other BN-related projects l l DBNS for discrete monitoring (Ph. D, 1992) Approximate BN inference algorithms based on a mutual information measure for relevance (with Nathalie Jitnah, ICONIP 97, ECSQARU 97, PRICAI 98, AI 99) l l Plan recognition: DBNs for predicting users actions and goals in an adventure game (with David Albrecht, Ingrid Zukerman, UM 97, UMUAI 1999, PRICAI 2000) Bayesian Poker (with Kevin Korb, UAI’ 99, honours students) 26

Other BN-related projects (cont. ) l l l DBNs for ambulation monitoring and fall diagnosis (with biomedical engineering, PRICAI’ 96) Autonomous aircraft monitoring and replanning (with Ph. D. student Tim Wilkin, PRICAI 2000) Ecological risk assessment (2003 honours project with Water Studies Centre) l Writing a textbook! (with Kevin Korb) Bayesian Artificial Intelligence 27

Open Research Questions l Methodology for combining expert elicitation and automated methods » expert knowledge used to guide search » automated methods provide alternatives to be presented to experts l Evaluation measures and methods » may be domain depended l Improved tools to support elicitation » e. g. visualisation of d-separation l Industry adoption of BN technology 28