Классы задач P и NP Гэри М. , Джонсон Д. Вычислительные машины и труднорешаемые задачи: Пер. с англ. — М. : Мир, 1982. — 416 с. 1
Что такое -класс задач P? • мы рассматривали логарифмическую, линейную и полиномиальную сложность алгоритма. Но если обобщить эти виды сложности, то все их можно описать полиномом, у которого показатель степени логарифм, единица и величина больше единицы. • Эти задачи относятся к классу Р - классу задач полиномиальной сложности. Такие задачи называются также практически разрешимыми. • С другой стороны, полиномиальные алгоритмы, имеющие временную сложности типа n 100 или 1099 n 2, не могут считаться эффективными с практической точки зрения 2
Что такое -класс задач NP? • Алгоритмы, временная сложность которых не поддается полиномиальной оценке, называются "экспоненциальными". Большинство экспоненциальных алгоритмов — это варианты полного перебора. • Будем называть задачу труднорешаемой, если для ее решения не существует полиномиального алгоритма. • Класс практически неразрешимых задач образуют класс NP - недетерминированной полиномиальной сложности. • Сложность всех известных детерминированных алгоритмов, решающих эти задачи, либо экспоненциальна, либо факториальна. Сокращение NP происходит от английских слов Nondeterministic Polynomial (time), что переводится как недетерминированное полиномиальное время. Кроме того, всякая задача из Р принадлежит также и NP. 3
недетерминированные алгоритмы • Неформально класс NP можно определить с помощью понятия, которое мы будем называть недетерминированным алгоритмом. • Такой алгоритм состоит из двух различных стадий — стадии угадывания и стадии проверки. • Именно понятие полиномиальной "проверяемости" позволяет выделить задачи класса NP. • Отметим, что проверяемость за полиномиальное время не влечет разрешимости за полиномиальное время. 4
Пример • К классу NP относится задача о коммивояжере. • Эту задачу можно применять, например, для определения порядка эффективного сбора мусора из баков на улицах города или выбора кратчайшего пути распространения информации по всем узлам компьютерной сети. • Предположим, что у нас есть алгоритм, способный подсчитать стоимость путешествия через 15 городов в указанном порядке. Если за секунду такой алгоритм способен пропустить через себя 100 вариантов, то ему потребуется больше четырех веков, чтобы исследовать все возможности и найти кратчайший путь. Даже если в нашем распоряжении имеется 400 компьютеров, все равно у них уйдет на это год, а ведь мы имеем дело лишь с 15 городами. • Можно ли найти кратчайший путь, не просматривая их все? До сих пор никому не удалось придумать алгоритм, который не занимается, по существу, просмотром всех путей. . 5
Как различить Р и NP задачи? • Для отнесения задачи к тому или иному классу используют задачу распознавания. • Задачей распознавания свойств называется задача, решениями которой могут быть либо "да", либо "нет". • Нас интересует классификация задач распознавания по их сложности. Обозначим через Р класс задач распознавания, которые могут быть решены некоторым полиномиальным алгоритмом. • Другими словами, Р — это класс относительно простых задач распознавания, для которых существуют эффективные алгоритмы. Например • СВЯЗНОСТЬ ГРАФА • ПУТЬ В ОРГРАФЕ • МИНИМАЛЬНОЕ ОСТОВНОЕ ДЕРЕВО • Все эти задачи принадлежат к классу Р. В каждом случае для любой индивидуальной задачи существует эффективный способ узнать, какой будет ответ да или 6 нет.
• Как правило, все задачи можно разделить на следующие классы: – – класс Р класс NPС – класс NP полных задач класс NPI – класс задач имеющих промежуточную сложность между Р и NP – класс со-NP – класс NP задач с противоположным ответом. • Напомним, что класс NP в качестве подклассов содержит класс Р и класс NP-полных задач (сокращенно NPC). В предположении Р NP эти два класса не пересекаются. • Если Р NP, то NP не может совпадать также и с классом P U NPC. Обозначим через NPI класс NP(P U NPC) задач, имеющих "промежуточную" сложность (между Р и NP). 7
NP-ПОЛНЫЕ ЗАДАЧИ • Класс NP-полных задач обладает следующими свойствами. – Никакую NP-полную задачу нельзя решить никаким известным полиномиальным алгоритмом (несмотря на настойчивые усилия многих блестящих исследователей в течение целых десятилетий). – Если существует полиномиальный алгоритм для какой-нибудь NP-полной задачи, то существуют полиномиальные алгоритмы для всех NР-полных задач. 8
Практическое значения понятия NP-полной задачи • исследователь, который сталкивается с новой задачей и не может найти для нее эффективного алгоритма, имеет теперь возможность попытаться доказать, что задача NPполна. • Такой подход во-первых, убережет исследователя от дальнейших тщетных попыток алгоритмически решить задачу. Кроме того, если о задаче известно, что она NPполна, то обычно появляется желание добиться менее амбициозных целей, чем построение алгоритма, который всегда находит точное решение и время работы которого никогда не превышает данной полиномиальной оценки. • Для доказательства NP-полноты можно воспользоваться одним из нескольких возможных подходов. 9
Фундамент теории NP-полных задач (заложен в работе С. Кука) положение 1 • если одна задача сводится за полиномиальное время к другой, то любой полиномиальный алгоритм решения второй задачи может быть превращен в полиномиальный алгоритм решения первой. 10
Фундамент теории NP-полных задач (заложен в работе С. Кука) положение 2 • Существует класс задач распознавания свойств (класс NP), которые могут быть решены за полиномиальное время на недетерминированном вычислительном устройстве. • Большинство не поддающихся решению задач, которые встречаются на практике, после переформулировки их в виде задач распознавания попадают в этот класс. 11
Фундамент теории NP-полных задач (заложен в работе С. Кука) положение 3 • доказано, что одна конкретная задача из NP, называемая задачей о выполнимости, обладает тем свойством, что всякая другая задача из класса NP может быть сведена к ней за полиномиальное время. • Таким образом, если задача о выполнимости может быть решена за полиномиальное время, то и любая задача из класса NP полиномиально разрешима, • Если какая-то задача из NP труднорешаема, то и задача о выполнимости также должна быть труднорешаемой. • Таким образом, в некотором смысле задача о выполнимости — "самая трудная" в классе NP. 12
Фундамент теории NP-полных задач (заложен в работе С. Кука) положение 4 • Другие задачи из класса NP могут быть, аналогично задаче о выполнимости, самыми "трудными" представителями класса NP. • Относительно широкого круга других задач доказано, что они по трудности эквивалентны этим задачам, а сам класс эквивалентности, состоящий из "самых трудных" задач из NP, получил название "класс NP-полных задач". 13
ПОЛИНОМИАЛЬНАЯ СВОДИМОСТЬ И NP-ПОЛНЫЕ ЗАДАЧИ • для доказательства полиномиальной сводимости, необходимо найти некоторую исходную NP-полную задачу. Такую задачу дает нам фундаментальная теорема Кука. • Теорема Кука. Задача ВЫПОЛНИМОСТЬ есть NP-полная задача. • Доказательства NP-полноты очень сложны. Однако, если известна одна NP-полная задача, то процедура доказательства NP-полноты других задач значительно упрощается. • Для доказательства NP-полноты задачи П NP достаточно показать, что какая-нибудь из известных NPполных задач П' может быть сведена к П. 14
Процесс доказательства NP-полноты задачи распознавания П состоит из четырех шагов: • доказательства того, что П лежит в NP; • выбора известной NP-полной задачи П'; • построения функции f, сводящей известную NP-полную задачу П' к задаче П, • доказательства того, что функция f осуществляет полиномиальное сведение. 15
ШЕСТЬ ОСНОВНЫХ NP-ПОЛНЫХ ЗАДАЧ • шесть задач входят в число тех, которые могут служить «основным ядром» списка известных NP-полных задач. • 3 -ВЫПОЛНИМОСТЬ (3 -ВЫП). • ТРЕХМЕРНОЕ СОЧЕТАНИЕ(З-С) • ВЕРШИННОЕ ПОКРЫТИЕ (ВП) • КЛИКА • ГАМИЛЬТОНОВ ЦИКЛ (ГЦ) • РАЗБИЕНИЕ 16
НЕКОТОРЫЕ МЕТОДЫ ДОКАЗАТЕЛЬСТВА NP-ПОЛНОТЫ • Методы, используемые при доказательстве результатов об NP-полноте, меняются почти в столь же широких пределах, как и сами NPполные задачи. • Однако имеется несколько общих приемов доказательства, которые часто встречаются и могут подсказать путь к доказательству NPполноты новой задачи. Они называются: – (а) сужение задачи, – (б) локальная замена – (в) построение компоненты 17
Метод сужения • самый простой и, вероятно, наиболее часто встречается. Его можно рассматривать скорее как иной взгляд на задачу, а не как стандартный способ доказательства NP-полноты. • Вместо того чтобы пытаться свести одну из известных NP-полных задач к заданной, мы концентрируем внимание на последней и пытаемся отбросить "несущественные" ее детали с тем, чтобы получилась известная NP-полная задача. • Ниже приведено несколько примеров задач, NP-полнота которых доказывается методом сужения: • (1) МИНИМАЛЬНОЕ ПОКРЫТИЕ • (2) МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ • (3) ИЗОМОРФИЗМ ПОДГРАФУ • (4) ОСТОВНОЕ ДЕРЕВО ОГРАНИЧЕННОЙ СТЕПЕНИ • (5) МИНИМАЛЬНЫЙ ЭКВИВАЛЕНТНЫЙ ОРИЕНТИРОВАННЫЙ ГРАФ • (6) РЮКЗАК • (7) РАСПИСАНИЕ ДЛЯ МУЛЬТИПРОЦЕССОРНОЙ СИСТЕМЫ 18
Анализ метода сужения • из трех обсуждаемых подходов к установлению NP-полноты метод сужения в наибольшей степени выигрывает от наличия обширного списка NP-полных задач, сверх основных шести задач и их вариантов. • Многие возникающие на практике задачи представляют собой просто более сложные версии задач из списка NP-полных задач, и способность усмотреть этот факт во многих случаях позволяет быстро доказать NP-полноту методом сужения. 19
Локальная замена • Этот метод состоит в том, что выбирается некоторое характерное свойство известной NP-полной задачи, с помощью него образуется семейство основных модулей, а соответствующие индивидуальные задачи заданной задачи получаются путем единообразной замены каждого основного модуля некоторой другой структурой. 20
Построение компонент • Последний и наиболее сложный из рассматриваемых нами! методов доказательств NP-полноты — это построение компонент. • Основная идея таких доказательств заключается в том, чтобы с помощью составных частей рассматриваемой задачи сконструировать некоторые "компоненты", соединяя которые можно "реализовать" индивидуальные задачи известной NP-полной задачи. 21
Применение теории NPполноты для анализа задач • Анализ начинается с вопроса: "Можно ли рассматриваемую задачу решить полиномиальным алгоритмом? " • В противном случае возникает второй вопрос: "Верно ли, что рассматриваемая задача NP-полна? « • В большинстве случаев найти ответ трудно, ибо зачастую задачи, разрешимые за полиномиальное время, очень незначительно отличаются от NP-полных задач • при анализе задач лучше пользоваться двусторонним подходом. Пытаясь с одной стороны доказать NP-полноту задачи, одновременно целесообразно искать полиномиальный алгоритм ее решения. • Неудачи в доказательстве NP-полноты задачи могут породить идею алгоритма ее решения, а неудачи в построении алгоритма могут указать путь к доказательству NP-полноты задачи. 22
Пример 23
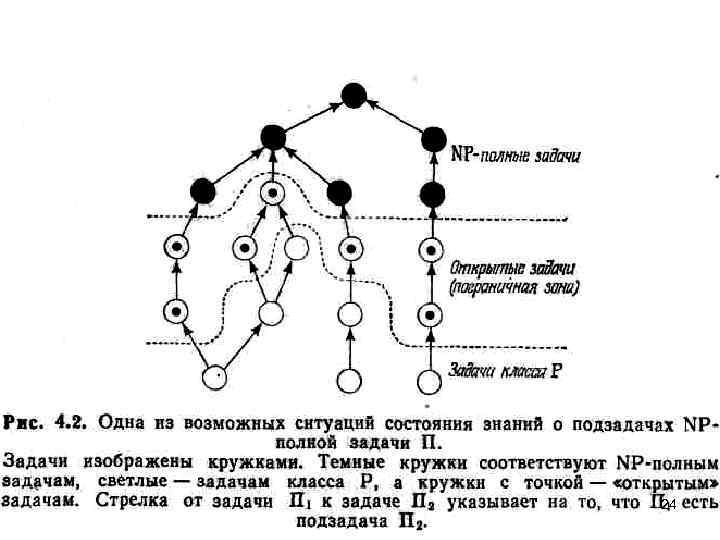24
Алгоритм с псевдополиномиальным временем работы • NP-полнота различных задач на практике в значительной степени зависит от входных данных. Если бы на величину этих чисел заранее было бы наложено какое-либо ограничение, то для решения этих задач возможны полиномиальные алгоритмы. В дальнейшем для выделения алгоритмов, обладающих этим свойством, мы введем термин "алгоритм с псевдополиномиальным временем работы". • Например, в задачах теории расписаний (где числа представляют собой длительности заданий) появление слишком больших чисел мало вероятно, поскольку мы собираемся выполнять задания реально, и если какое-то из них требует чрезвычайно большого времени, то мы просто будем не в состоянии его закончить. В других задачах, где числа представляют собой эмпирически измеренные величины, доступная точность измерения ограничивает 25 пределы изменения чисел, к которым наш алгоритм должен быть применим.
Отыскание псевдополиномиального алгоритма • отыскание псевдополиномиального алгоритма для решения NP-полной задачи с числовыми параметрами — вопрос достойный исследования. Можно показать, что если Р NP, то для решения некоторых из них не может существовать даже псевдополиномиального алгоритма 26
Подходы к решению NP-полных задач • Подходы к решению NP-полных задач можно было бы разбить на две общие категории. • К первой категории относятся подходы, в которых делается попытка максимального сокращения объема перебора, хотя при этом и признается неизбежность экспоненциального времени работы. • К наиболее широко используемым приемам сокращения перебора относятся приемы, основанные на методе "ветвей и границ" или методе "неявного перебора". • Эти приемы состоят в построении "частичных решений", представленных в виде дерева поиска, и применении мощных методов построения оценок, позволяющих опознать бесперспективные частичные решения, в результате чего от дерева поиска на одном шаге отсекается целая ветвь. 27
Другие подходы к решению NP-полных задач • Известны и другие подходы, когда процесс поиска организован иначе (они используются иногда совместно с методом ветвей и границ). • К ним относятся метод динамического программирования, методы отсечений и метод Лагранжа. • Кроме того, в худшем случае иногда оказывается возможным в значительной степени уменьшить сложность полного перебора за счет более удачного выбора объектов, к которым он применяется. 28
Эвристические алгоритмы решения NP-полных задач • • • Подходы, относящиеся ко второй категории, применимы исключительно к оптимизационным задачам (это однако не является слишком сильным ограничением, поскольку огромное количество задач, возникающих на практике, естественно формулируются как оптимизационные) и включают прием, который можно назвать "снижение требований". Он заключается в отказе от поиска оптимального решения и в нахождении вместо этого "хорошего" решения за приемлемое время. Алгоритмы, основанные на этом приеме, обычно называются "эвристическими", поскольку они используют различные разумные соображения без строгих обоснований. Методы, применяемые для построения алгоритмов такого типа, сильно зависят от специфики задачи, хотя и удалось выделить несколько руководящих принципов, которые могут служить полезной отправной точкой. Наиболее широко применяется так называемый метод "локального поиска", когда заранее выбранное множество локальных операций используется для последовательного улучшения начального решения до тех пор, пока такое улучшение возможно, в противном случае оказывается достигнутым "локальный оптимум". 29
Анализ эвристических алгоритмов • Эвристические алгоритмы, построенные этим и другими методами, на практике оказываются весьма удовлетворительными, хотя для получения удовлетворительных характеристик алгоритма обычно требуется довольно большая работа по его "доводке". В результате удается только в очень редких случаях заранее предсказать и оценить поведение таких алгоритмов. Вместо этого такие алгоритмы оцениваются и сравниваются на основе сочетания эмпирических данных и аргументов, опирающихся на здравый смысл. • Однако совсем недавно был получен ряд результатов, которые показали, что эвристические алгоритмы не всегда столь сложны для формального анализа. В некоторых случаях удается доказать, что решения, получаемые эвристическим алгоритмом, всегда будут отличаться в процентном отношении от оптимального решения не более чем на определенную величину. Подобные результаты можно рассматривать как "оценки погрешности" алгоритмов 30