Адонкина, Поверхности.ppt
- Количество слайдов: 136

Классификация поверхностей
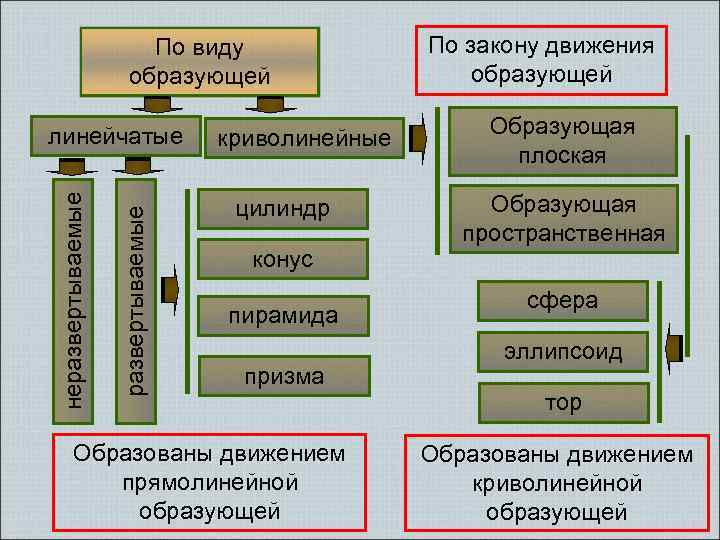
По виду образующей развертываемые неразвертываемые линейчатые криволинейные цилиндр конус пирамида призма Образованы движением прямолинейной образующей По закону движения образующей Образующая плоская Образующая пространственная сфера эллипсоид тор Образованы движением криволинейной образующей
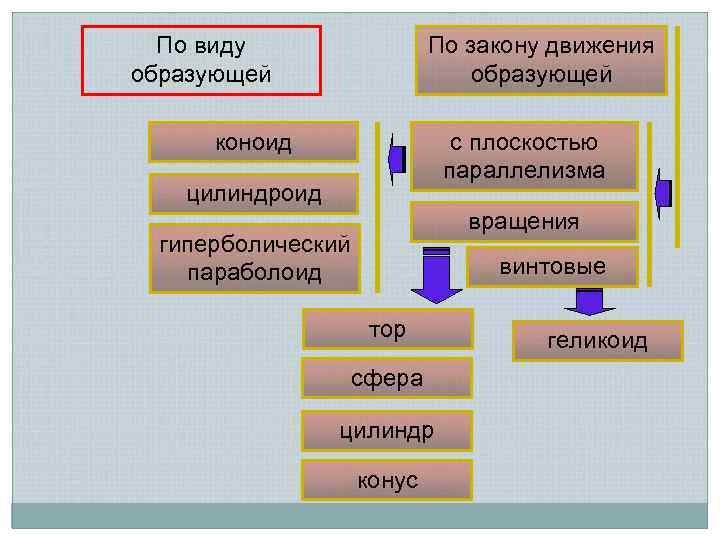
По виду образующей По закону движения образующей коноид с плоскостью параллелизма цилиндроид вращения гиперболический параболоид винтовые тор сфера цилиндр конус геликоид

Кривые линии
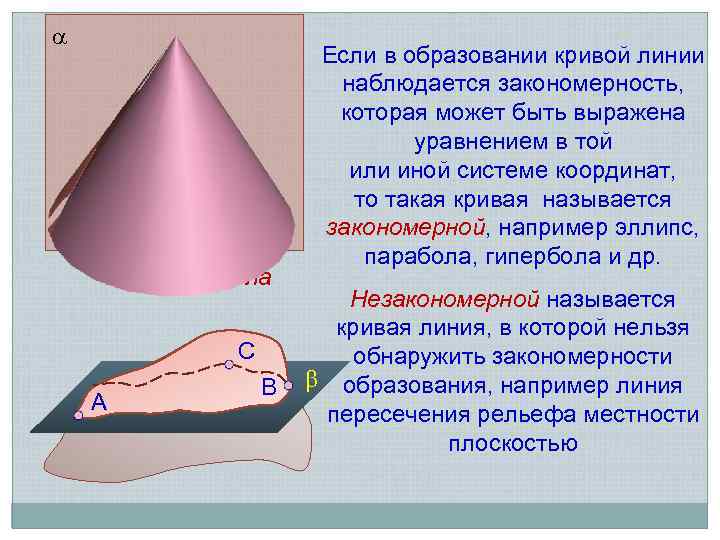
гипербола С А В Если в образовании кривой линии наблюдается закономерность, которая может быть выражена уравнением в той или иной системе координат, то такая кривая называется закономерной, например эллипс, парабола, гипербола и др. Незакономерной называется кривая линия, в которой нельзя обнаружить закономерности образования, например линия пересечения рельефа местности плоскостью

Если уравнение кривой линии представляет собой алгебраический многочлен, то она называется алгебраической Если кривую нельзя задать алгебраическим многочленом, то она называется трансцендентной

Линии, все точки которых не принадлежат одной плоскости, называются пространственными Порядок алгебраической пространственной кривой определяется числом ее точек пересечения с плоскостью ℓ 2 1 Пi 4 3

Линии, все точки которых принадлежат одной плоскости, называются плоскими Порядок плоской алгебраической кривой определяется числом ее точек пересечения с прямой линией m ℓ 1 2
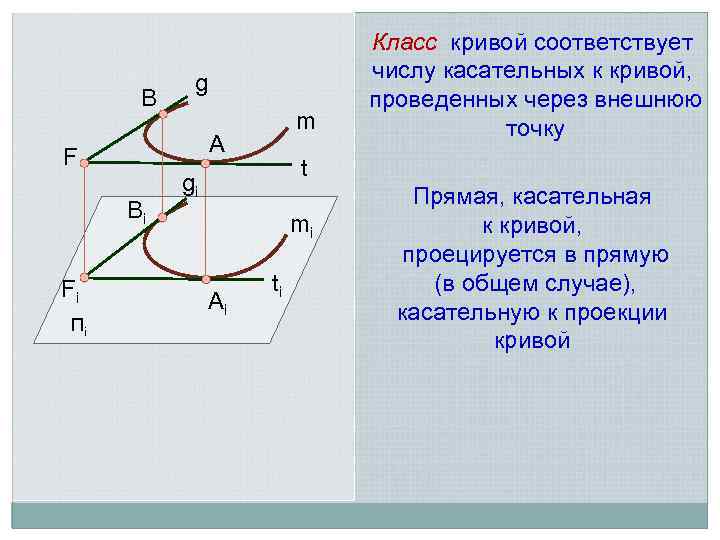
B Bi Пi m A F Fi g t gi mi Ai Класс кривой соответствует числу касательных к кривой, проведенных через внешнюю точку ti Прямая, касательная к кривой, проецируется в прямую (в общем случае), касательную к проекции кривой
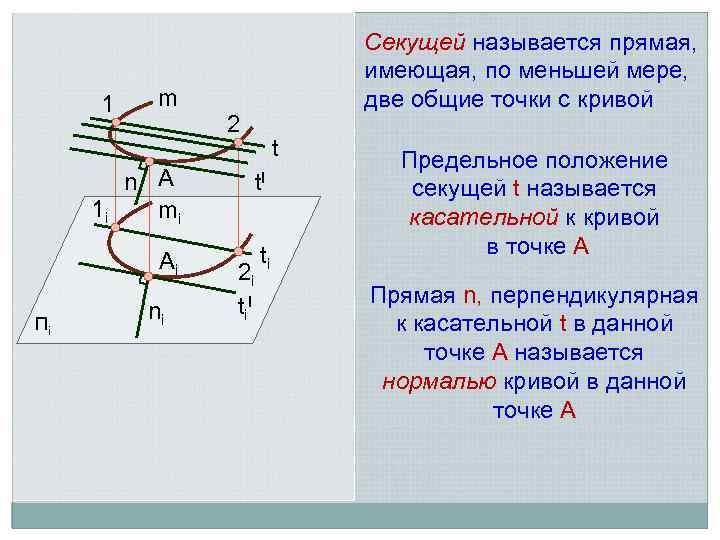
1 m Секущей называется прямая, имеющая, по меньшей мере, две общие точки с кривой 2 t n A 1 i mi Ai Пi t. I ti ni 2 i t i. I Предельное положение секущей t называется касательной к кривой в точке А Прямая n, перпендикулярная к касательной t в данной точке А называется нормалью кривой в данной точке А

Особые точки кривой

Точки перегиба (Н) – точки, в которых кривая проходит на другую сторону касательной прямой, сохраняя касание Двойная или узловая точка (А) – это точка, в которой кривая пересекает сама себя Точки возврата первого ряда (В), в которой кривая подходит к точке двумя ветвями, имеющими в точке В общую касательную и расположенными по разные стороны от касательной Точки возврата второго ряда С, в которой кривая подходит к точке двумя ветвями, имеющими в точке С общую касательную, расположенную (вблизи точки С) по одну сторону от обеих ветвей кривой

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

Линия пересечения поверхности с плоскостью является линией, одновременно принадлежащей поверхности и секущей плоскости Поэтому для ее построения необходимо отыскать такие точки и линии, которые одновременно принадлежат данной поверхности и заданной секущей плоскости Замкнутая фигура, образованная линией пересечения поверхности тела секущей плоскостью, называется сечением

Пересечение проецирующей поверхности с проецирующей плоскостью

Прямой круговой цилиндр занимает горизонтально проецирующее положение
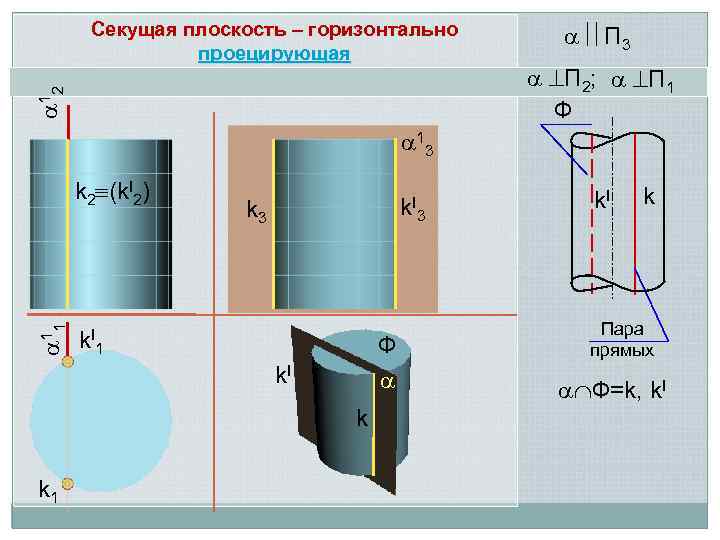
12 Секущая плоскость – горизонтально проецирующая П 3 П 2; П 1 Ф 13 11 k 2 (k. I 2) k. I 3 k. I 1 Ф k. I k k 1 k. I k Пара прямых Ф=k, k. I
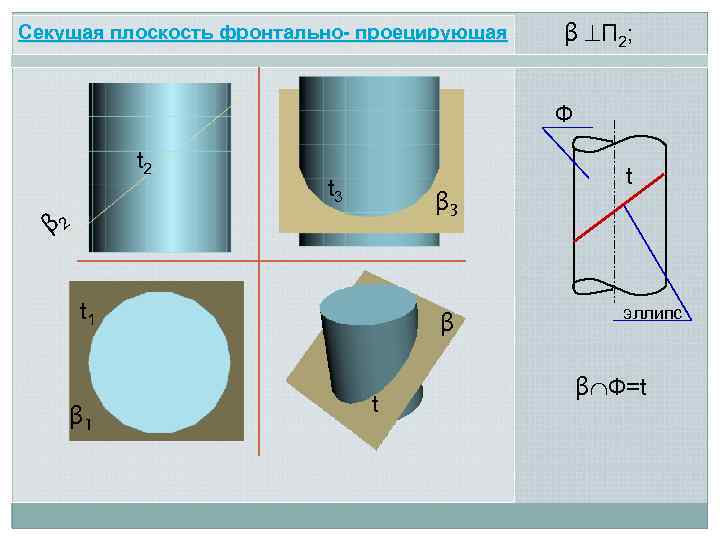
Секущая плоскость фронтально- проецирующая β П 2; Ф t 2 t 3 β 2 t 1 β t t эллипс β Ф=t
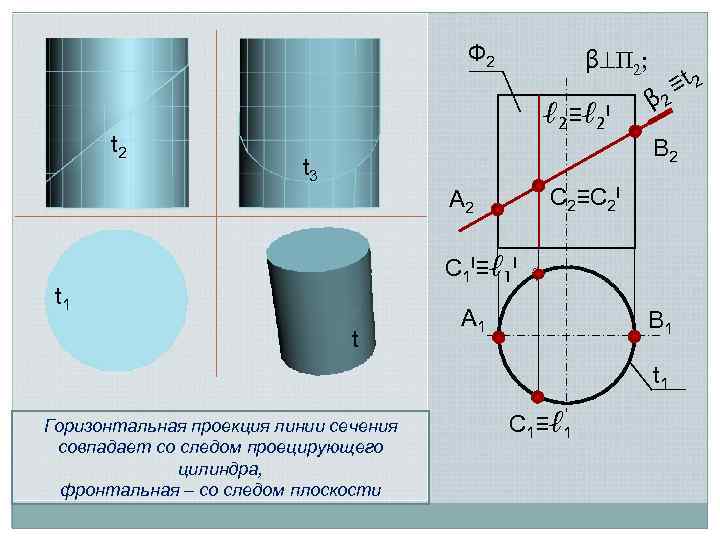
Ф 2 t 2 β П 2; ℓ 2≡ℓ 2 I t 3 β ≡t 2 2 В 2 С 2≡С 2 I А 2 С 1 I≡ℓ 1 I t 1 t А 1 В 1 t 1 Горизонтальная проекция линии сечения совпадает со следом проецирующего цилиндра, фронтальная – со следом плоскости С 1≡ℓ 1
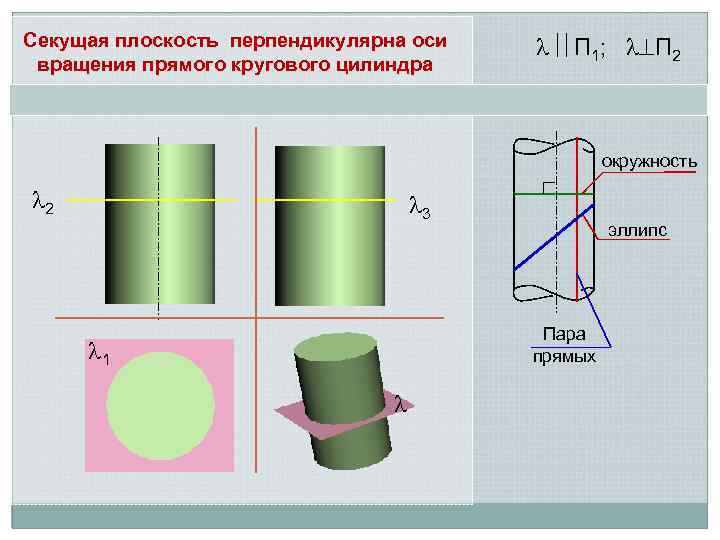
Секущая плоскость перпендикулярна оси вращения прямого кругового цилиндра П 1; П 2 окружность 2 3 эллипс Пара прямых 1
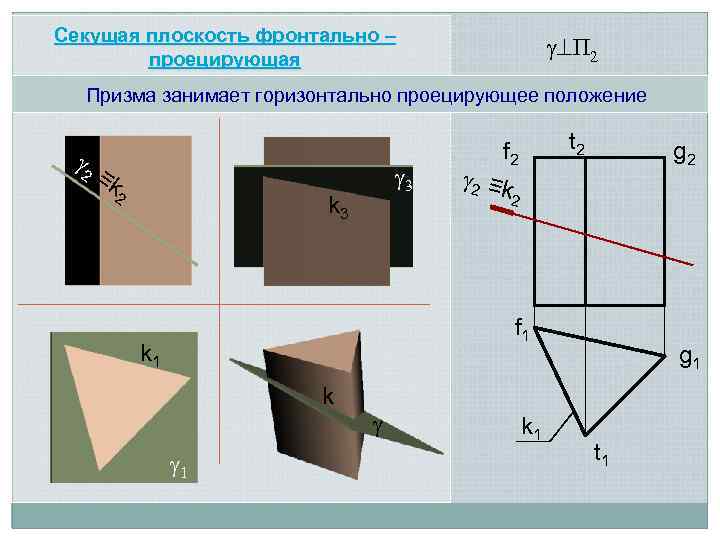
Секущая плоскость фронтально – проецирующая П 2 Призма занимает горизонтально проецирующее положение 2 ≡k 2 3 k 3 t 2 f 2 g 2 2 ≡k 2 f 1 k 1 k 1 g 1 t 1

Пересечение поверхности общего положения с проецирующей плоскостью

Конические сечения (коники)

Аполлоний прославился в первую очередь выдающейся работой «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы Именно Аполлоний предложил общепринятые Аполлоний Пергский названия этих кривых; до него 262 год до н. э. их называли просто «сечениями конуса» http: //ru. wikipedia. org/wiki/Файл: Apollonios_of_Perga. jpeg
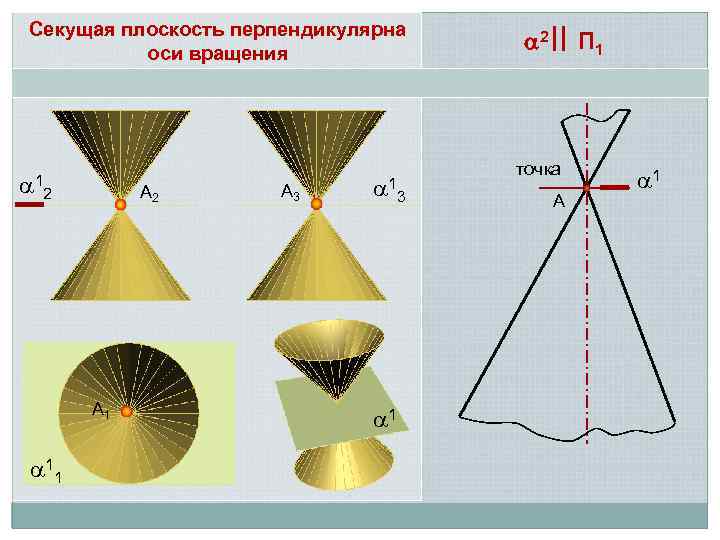
Секущая плоскость перпендикулярна оси вращения 1 А 2 2 А 1 11 А 3 1 2 П 1 точка А 1
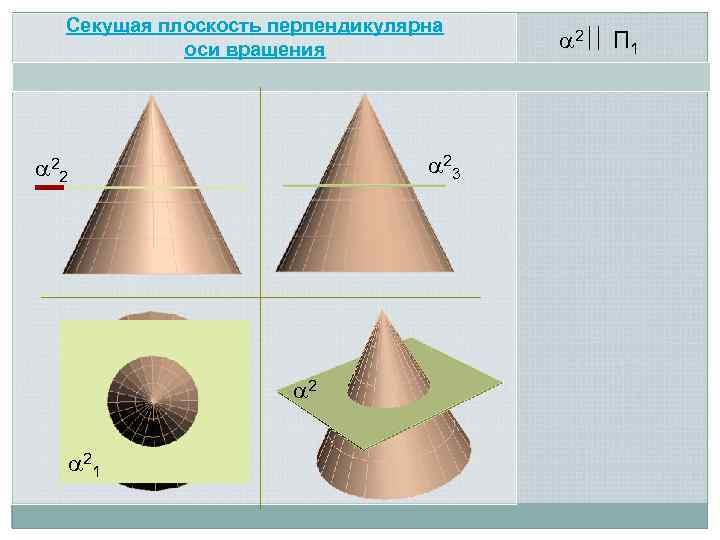
Секущая плоскость перпендикулярна оси вращения 23 22 2 21 2 П 1
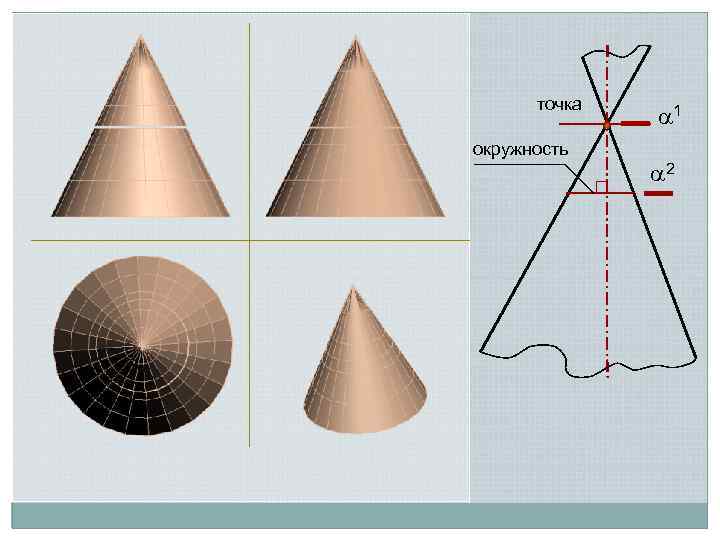
точка окружность 1 2
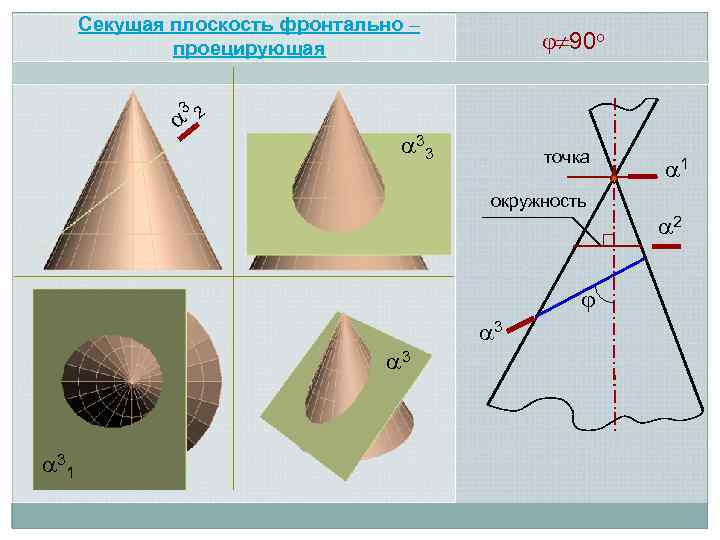
Секущая плоскость фронтально – проецирующая 90 о 3 2 33 точка окружность 3 3 31 1 2
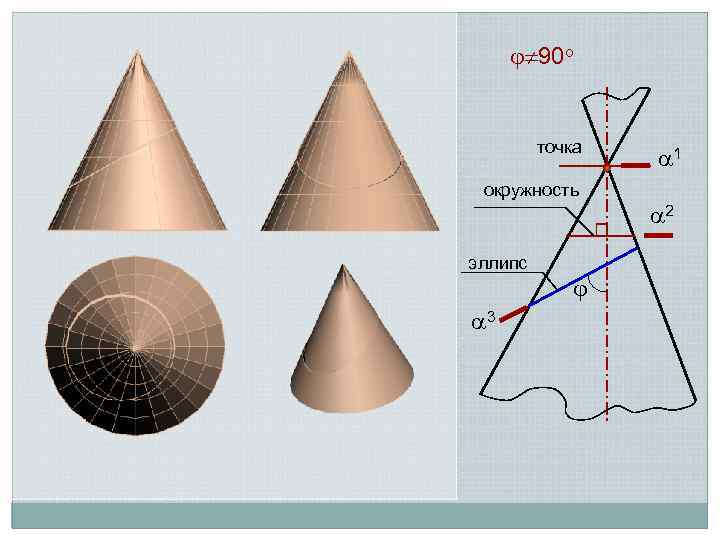
90 о точка окружность эллипс 3 1 2
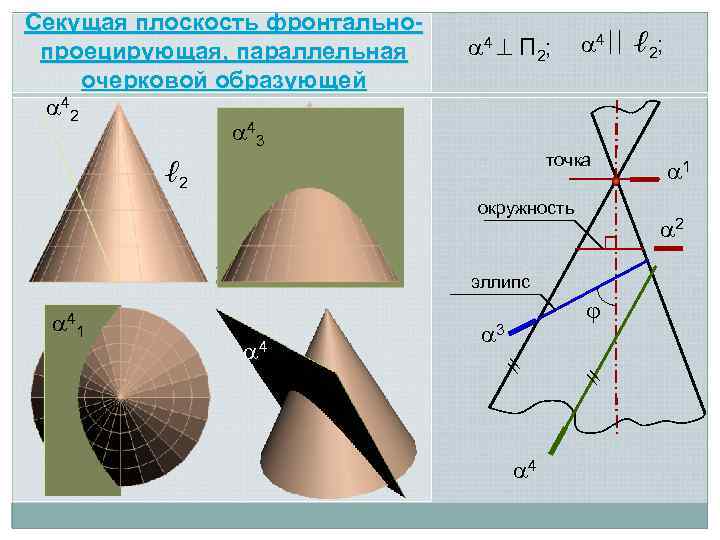
Секущая плоскость фронтальнопроецирующая, параллельная очерковой образующей 42 43 4 П 2; 4 ℓ 2; точка ℓ 2 окружность 2 эллипс 3 // 41 4 1
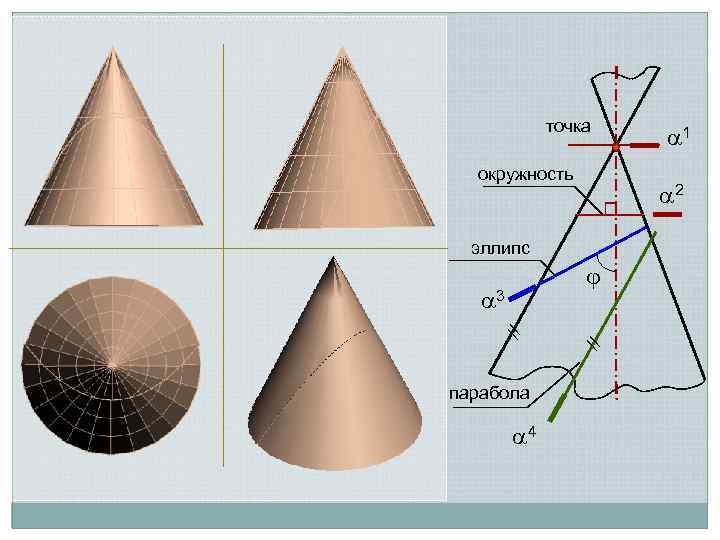
точка окружность 2 эллипс // // 3 парабола 4 1
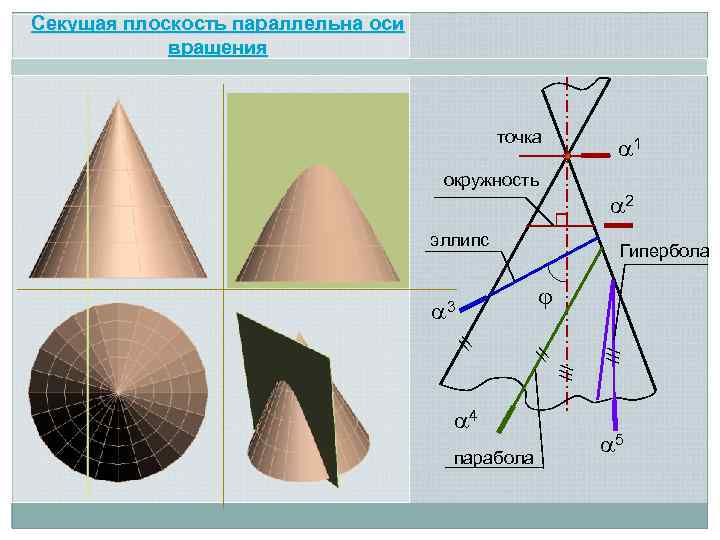
Секущая плоскость параллельна оси вращения точка 1 окружность 2 эллипс Гипербола /// // 3 4 парабола 5
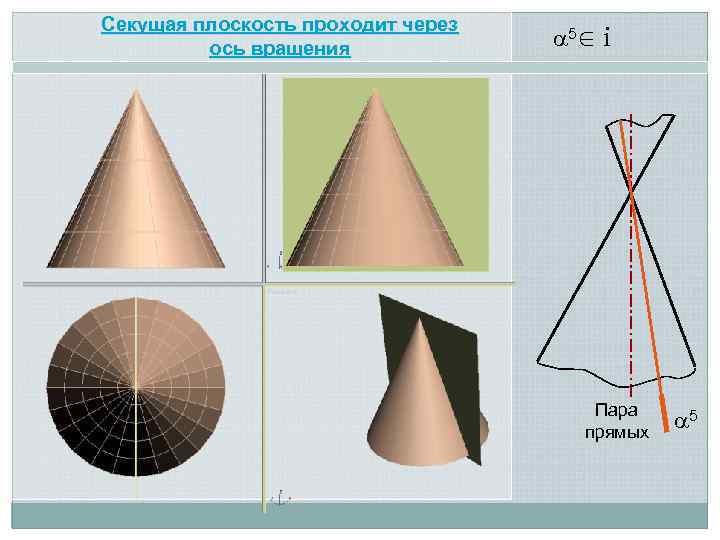
Секущая плоскость проходит через ось вращения 5∈ i Пара прямых 5
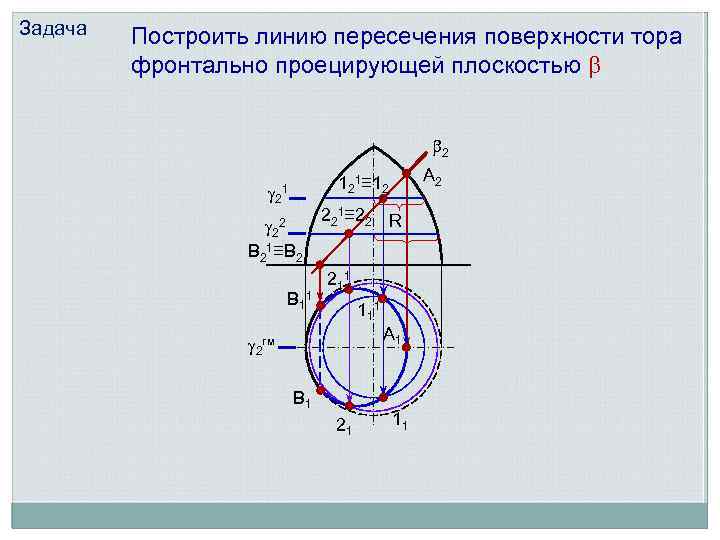
Задача Построить линию пересечения поверхности тора фронтально проецирующей плоскостью 2 2 А 2 121≡ 12 1 2 В 21≡В 2 2 В 11 221≡ 22 R 21 1 11 1 А 1 2 гм В 1 21 11

Пересечение поверхности общего положения с плоскостью общего положения

Обе проекции искомой линии пересечения строятся в плоскостях П 1 и П 2, с использованием метода секущих плоскостей или способом замены плоскостей проекций

Алгоритм решения задач на пересечение поверхности общего положения с плоскостью общего положения 1. Поверхность и плоскость пересекают вспомогательной плоскостью посредником . 2. Находят линию пересечения плоскостипосредника с поверхностью Ф: n = Ф . 3. Находят линию пересечения плоскостипосредника с заданной плоскостью : MN = . 4. Отмечают точки, в которых эти линии пересекутся: 1, 2 – MN n Точки 1 и 2, являясь общими для данных поверхности и плоскости будут точками искомой линии пересечения. 5. Для построения линии пересечения необходимо найти еще ряд точек (3, 4, 5…), используя плоскости-посредники
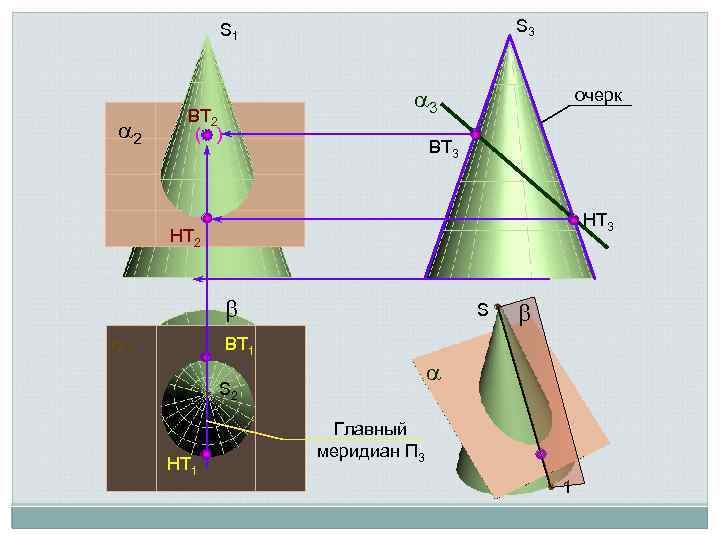
S 3 S 1 2 3 ВТ 2 ( ) очерк ВТ 3 НТ 2 1 S ВТ 1 S 2 НТ 1 Главный меридиан П 3 1
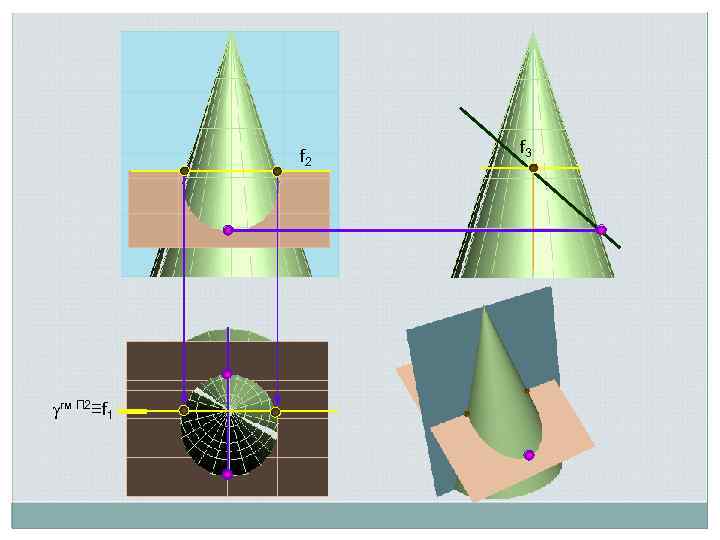
f 2 гм П 2≡f 1 f 3
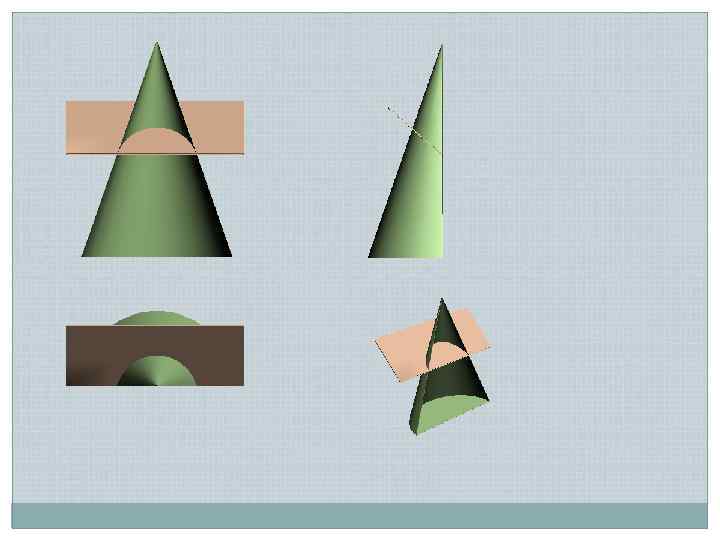
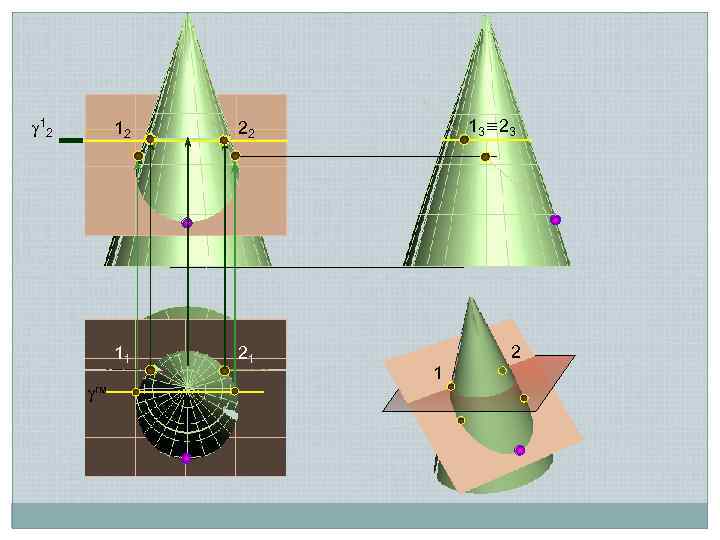
12 гм 22 13≡ 23 11 1 2 21 2 1
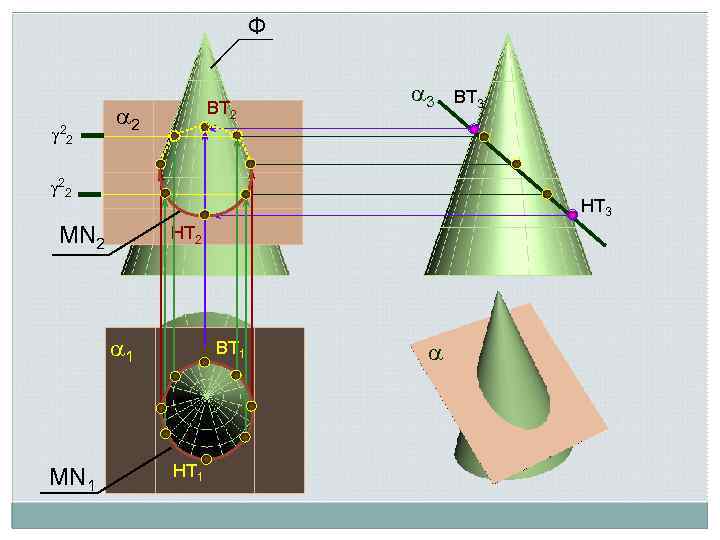
Ф 2 ВТ 2 2 3 ВТ 3 2 2 2 НТ 3 MN 2 НТ 2 1 MN 1 ВТ 1 НТ 1
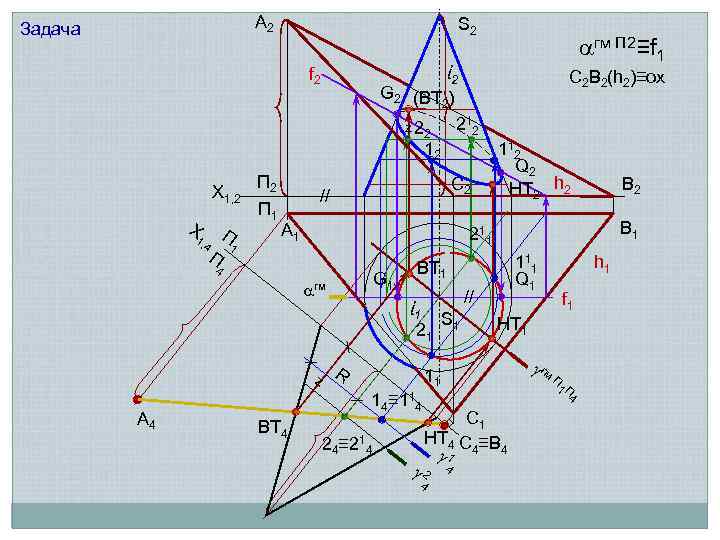
А 2 Задача S 2 ί 2 f 2 C 2 B 2(h 2)≡ox G 2 (ВТ ) 2 21 2 z 22 12 Х 1, 2 Х П 1, 4 П 1 П 2 П 1 С 2 // А 1 G 1 гм В 2 В 1 z 11 1 Q 1 ВТ 1 // ί 1 21 R S 1 24≡ 214 4 f 1 гм П 1 П 4 С 1 НТ 4 С ≡B 1 4 4 2 h 1 НТ 1 11 14≡ 114 ВТ 4 11 2 Q 2 НТ 2 h 2 21 1 4 А 4 гм П 2≡f 1 4

Пересечение прямой с поверхностью Алгоритм 1. Через прямую АВ проводят вспомогательную плоскость – посредник 2. Находят линию пересечения поверхности с плоскостью - k 3. Отмечают точки пересечения прямой АВ с линией k, точки 1 и 2 Количество точек пересечения прямой с поверхностью определяет порядок последней
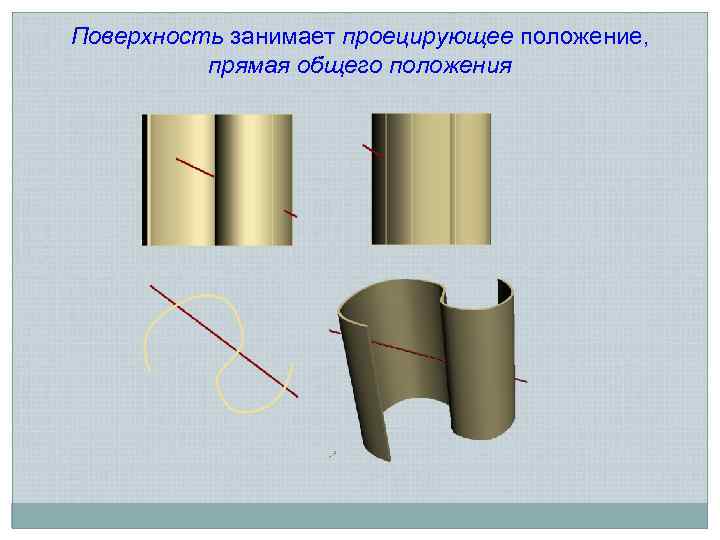
Поверхность занимает проецирующее положение, прямая общего положения
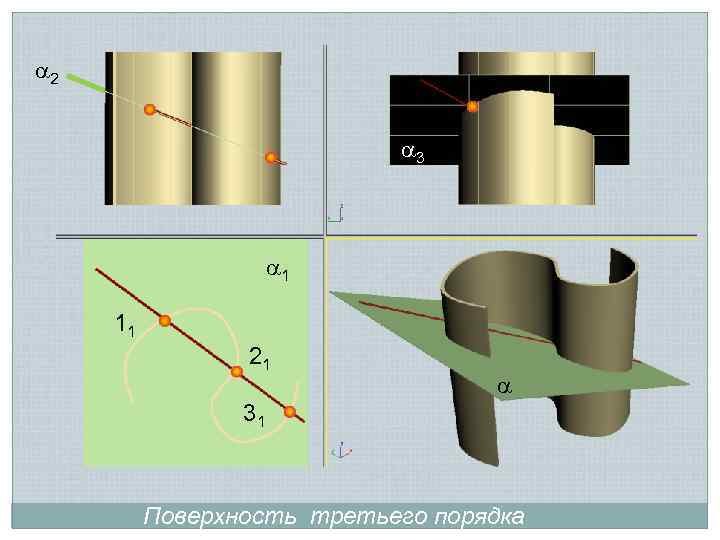
2 3 1 11 21 31 Поверхность третьего порядка
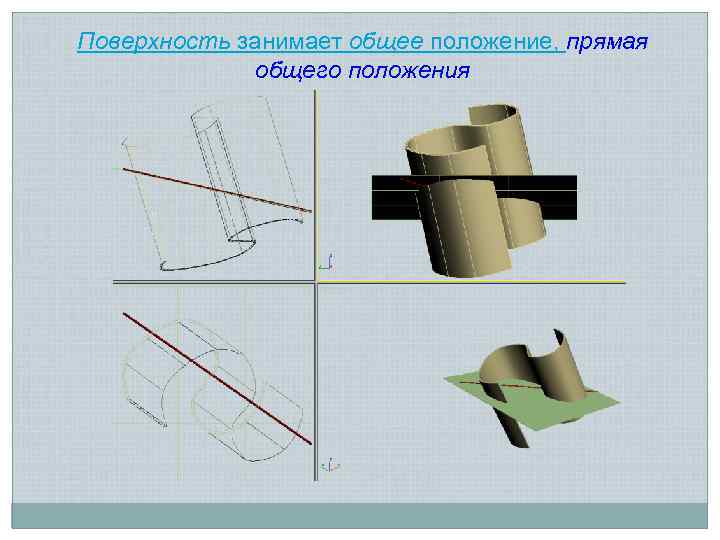
Поверхность занимает общее положение, прямая общего положения
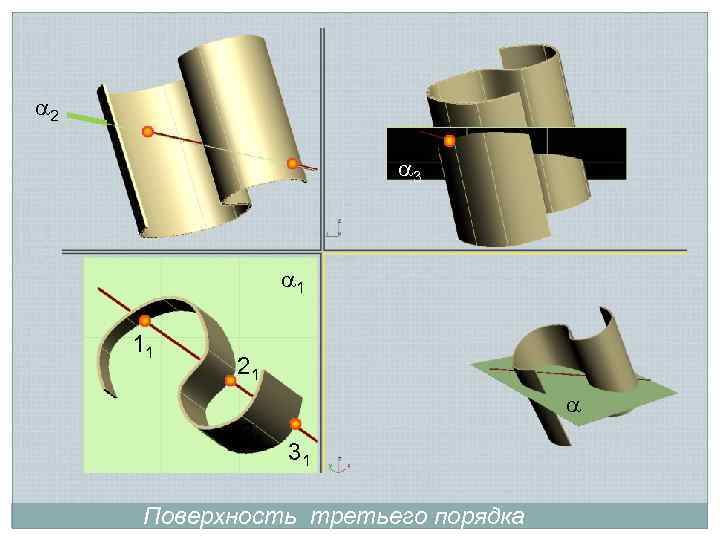
2 3 1 11 21 31 31 Поверхность третьего порядка

Пересечение многогранника с плоскостью

Сечение многогранника плоскостью В общем случае линия пересечения – плоская ломаная линия

способ ребер по точкам пересечения ребер многогранника с секущей плоскостью (задача на построение точки пересечения прямой с плоскостью) способ граней по линии пересечения граней многогранника с секущей плоскостью (задача на построение линии пересечения двух плоскостей)

Секущая плоскость – частного положения – точки искомой линии пересечения строятся по точкам пересечения выродившейся в прямую проекции секущей плоскости с одноименными проекциями ребер (образующих или других линий) данной поверхности
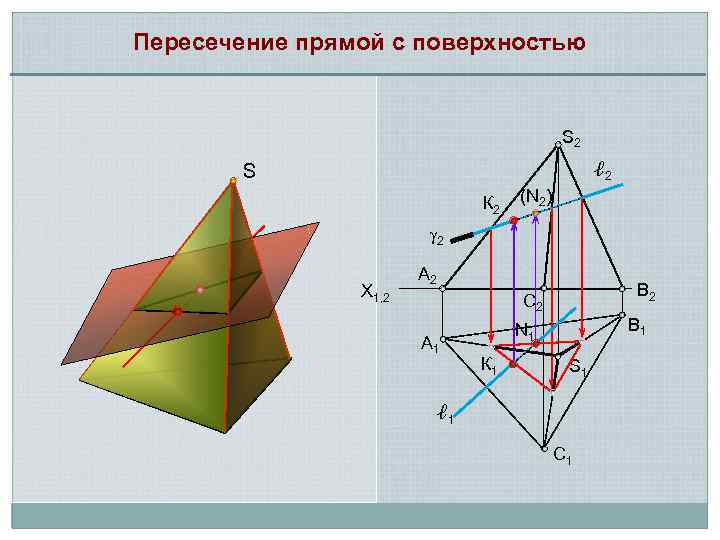
Пересечение прямой с поверхностью S 2 ℓ 2 S К 2 (N 2) 2 X 1, 2 А 2 В 2 С 2 А 1 В 1 N 1 К 1 S 1 ℓ 1 С 1

Алгоритм 1. Через прямую ℓ проводят вспомогательную плоскость-посредник 2. Находят линию пересечения поверхности с плоскостью – k 3. Отмечают точки пересечения прямой ℓ с линией k, точки 1 и 2 Количество точек пересечения прямой с поверхностью определяет порядок последней
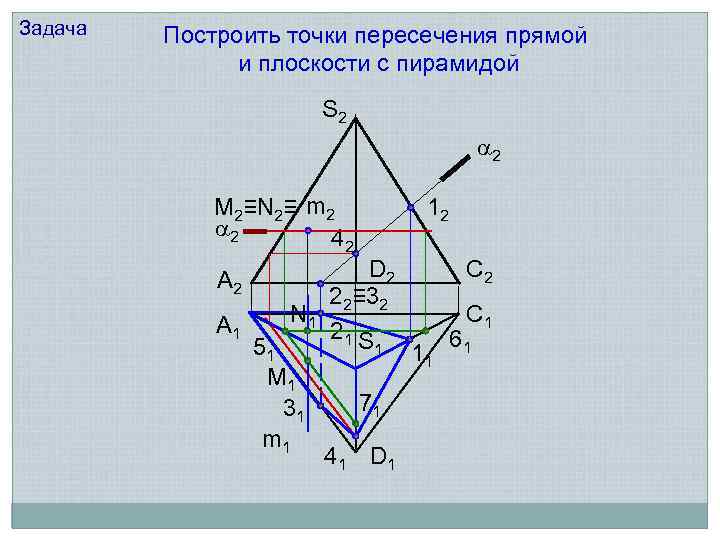
Задача Построить точки пересечения прямой и плоскости с пирамидой S 2 2 M 2≡N 2≡ m 2 2 42 A 1 12 D 2 22≡ 32 N 1 21 S 51 M 1 31 m 1 1 71 41 D 1 C 2 C 1 11 61

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ

Полное (проницание) – все образующие одной поверхности пересекаются со второй поверхностью. Линия пересечения распадается на две отдельные кривые Частичное (врезание)– часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения – замкнутая пространственная кривая

Теорема 1 Если две поверхности пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются
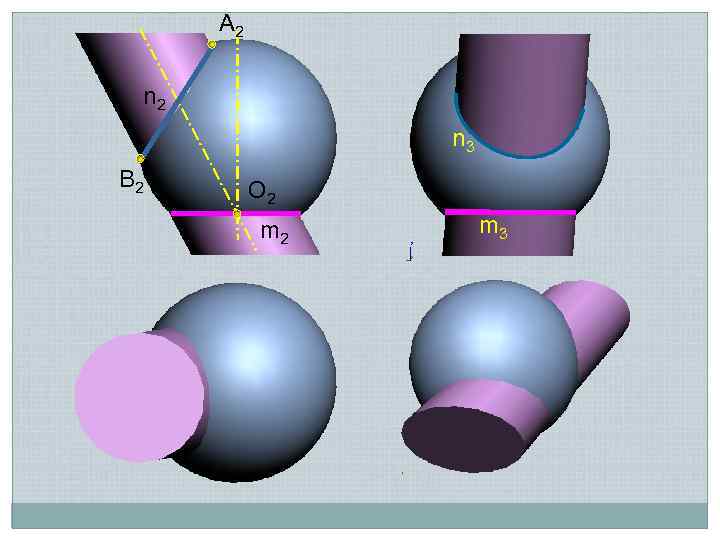
A 2 n 3 B 2 O 2 m 3

Одностороннее внутреннее соприкасание – пересекающиеся криволинейные поверхности имеют в одной точке общую плоскость касания Линия пересечения – замкнутая пространственная кривая, пересекающаяся сама с собой в точке касания (точка самопересечения)

Двойное соприкасание – пересекающиеся криволинейные поверхности имеют две общие касательные плоскости В пересечении участвуют все образующие одной поверхности и все образующие второй

Теорема (о двойном касании) Если две поверхности имеют касание в двух точках M и N, то линия перехода распадается на две плоские кривые 2 -го порядка, плоскости которых проходят через отрезок MN, соединяющий точки касания M N
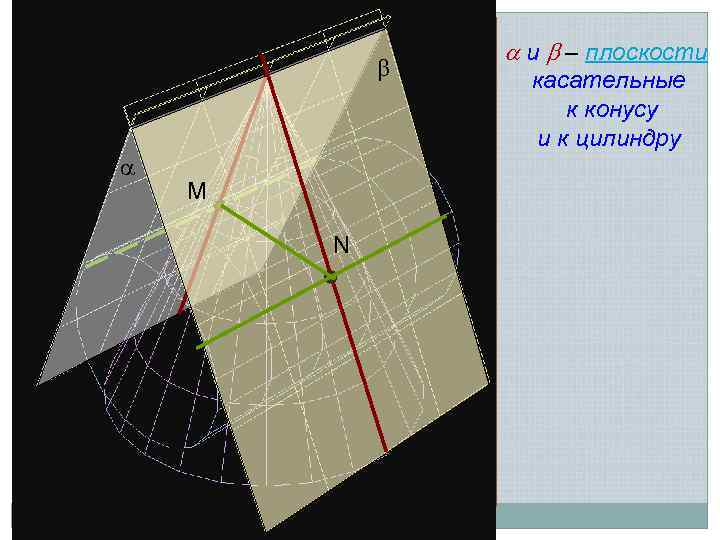
M N и – плоскости касательные к конусу и к цилиндру
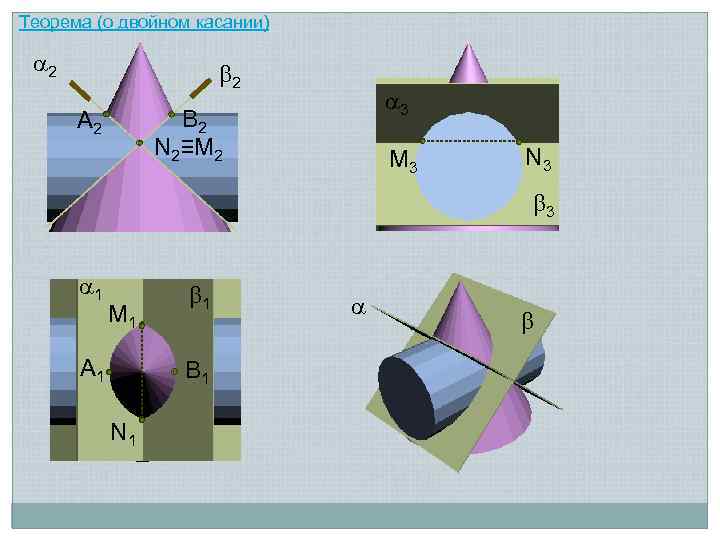
Теорема (о двойном касании) 2 2 3 B 2 N 2≡M 2 A 2 M 3 N 3 3 1 M 1 A 1 1 B 1 N 1
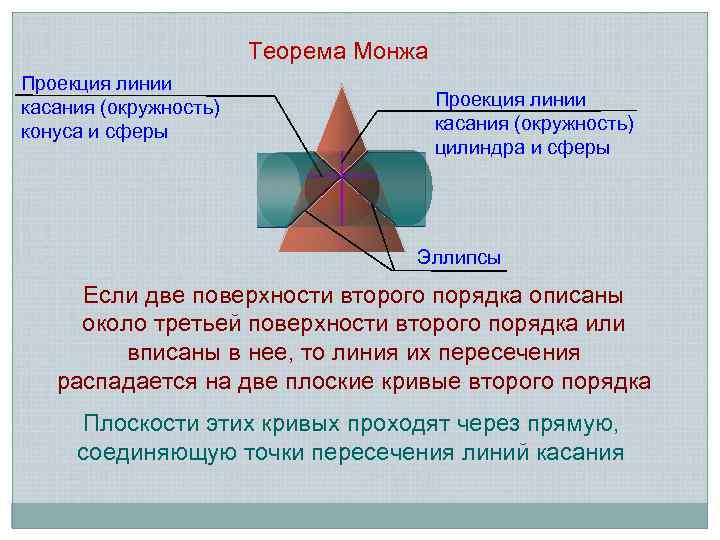
Теорема Монжа Проекция линии касания (окружность) конуса и сферы Проекция линии касания (окружность) цилиндра и сферы Эллипсы Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания

Пересечение поверхностей вращения способом секущих плоскостей
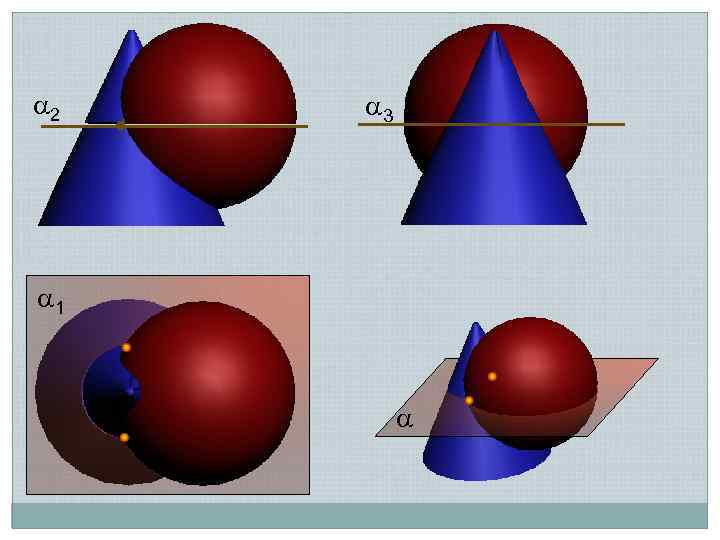
2 3 1

Алгоритм: 1. Заданные поверхности пересекаются вспомогательной плоскостью–посредником 2. Строят линии пересечения плоскости– посредника с заданными поверхностями 3. Отмечают точки пересечения полученных линий, которые и являются точками линии пересечения поверхностей
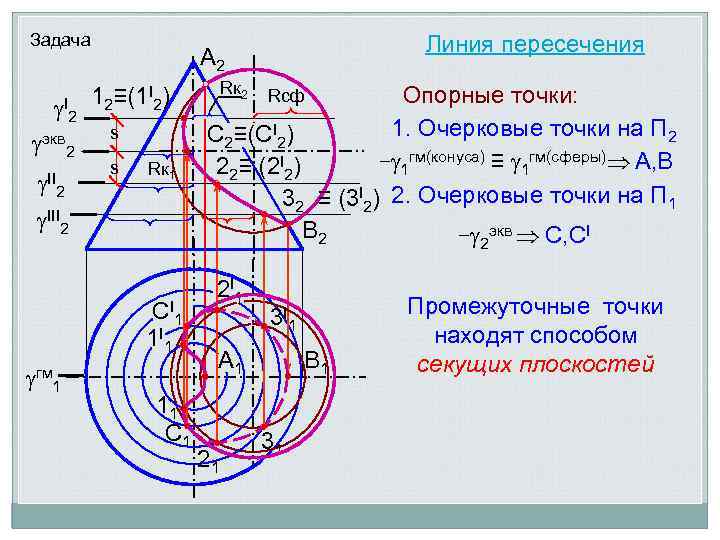
Задача I 2 экв 2 II А 2 12≡(1 I 2) s s Rк 1 2 III 2 CI 1 1 I 1 гм 1 Линия пересечения 11 C 1 Rк 2 Опорные точки: 1. Очерковые точки на П 2 C 2≡(CI 2) – 1 гм(конуса) ≡ 1 гм(сферы) А, В 22≡ (2 I 2) 32 ≡ (3 I 2) 2. Очерковые точки на П 1 В 2 – 2 экв С, СI 2 I 1 Rсф 3 I 1 А 1 21 B 1 31 Промежуточные точки находят способом секущих плоскостей

Пересечение поверхностей вращения Способ концентрических сфер
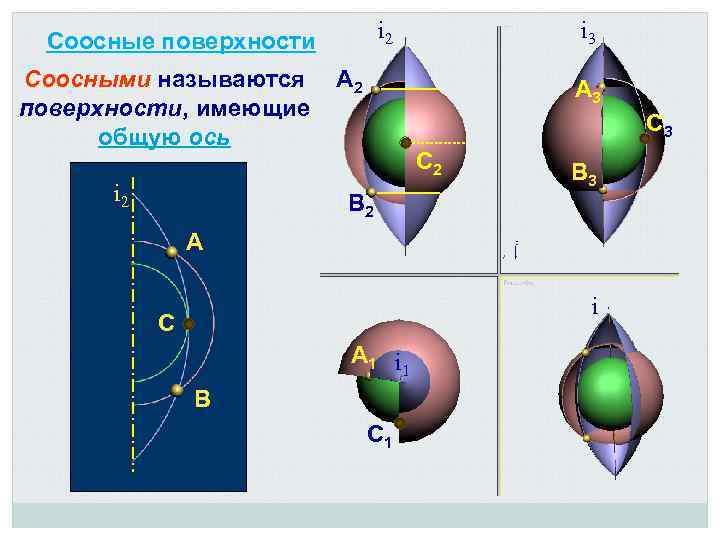
i 2 Соосные поверхности Соосными называются поверхности, имеющие общую ось i 2 i 3 А 2 А 3 С 2 В 3 В 2 А i С А 1 i 1 В С 1
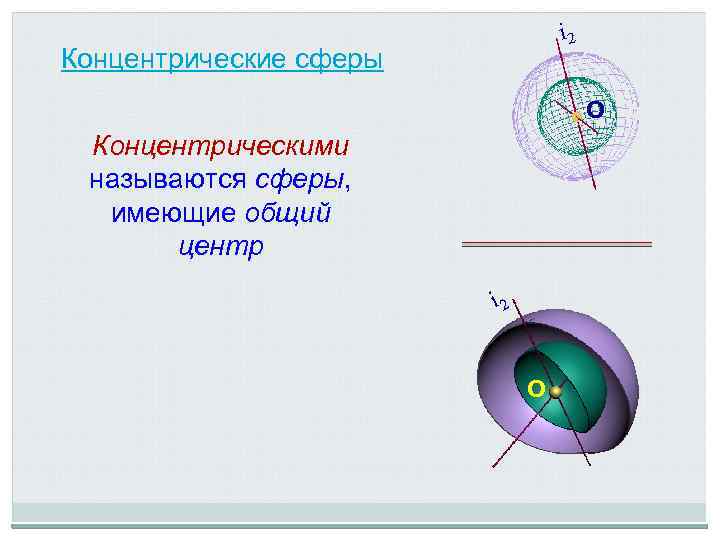
i 2 Концентрические сферы О Концентрическими называются сферы, имеющие общий центр i 2 О

Способ сфер применяется в случаях, когда: 1. Пересекаются поверхности вращения 2. Оси вращения поверхностей пересекаются 3. Пересекающиеся оси вращения образуют плоскость уровня, или проецирующую плоскость
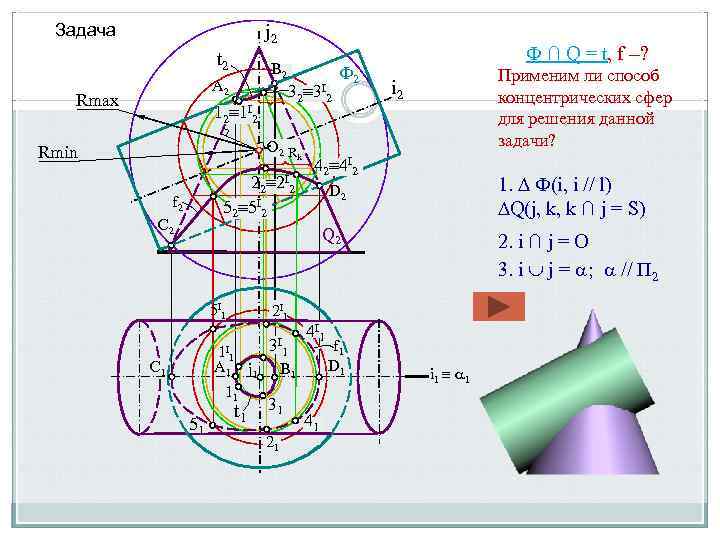
Задача j 2 t 2 B 2 A 2 Rmax 12 1 I 32 22 2 I 2 52 5 I 2 f 2 C 2 Ф 2 2 Применим ли способ концентрических сфер для решения данной задачи? i 2 2 О 2 R Rmin 3 I Ф ∩ Q = t, f –? k 42 4 I 2 1. Ф(i, i // l) Q(j, k, k ∩ j = S) D 2 Q 2 5 I 1 2 I 1 3 I 1 1 I 1 A 1 j 1 B 1 11 C 1 51 t 1 31 21 4 I 1 41 f 1 D 1 2. i ∩ j = О 3. i j = ; // П 2 i 1 1
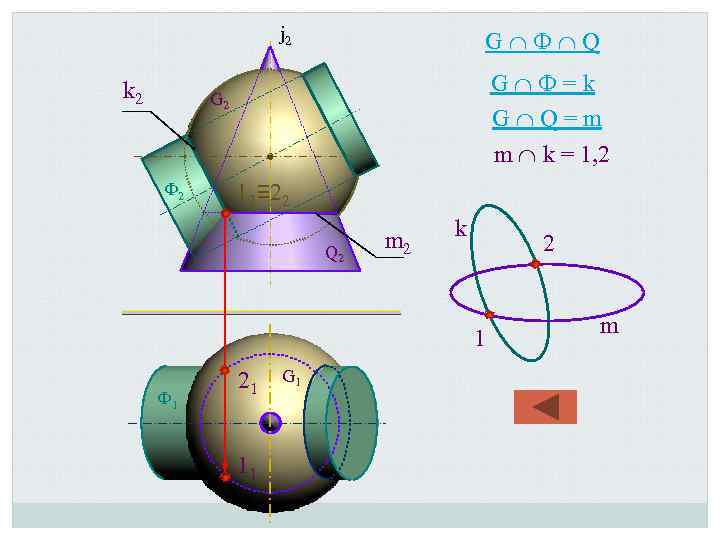
j 2 k 2 G Ф Q G Ф=k G Q=m m k = 1, 2 G 2 Ф 2 12≡ 22 Q 2 m 2 k 2 1 Ф 1 21 11 G 1 m

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Тентовые сооружения http: //www. verteco. ru/projects/? tag=1&val=2008 http: //www. prodayslona. ru/catalog/adds/element/82871/ http: //www. breezair. ucoz. ru/photo/1 -0 -114 -3 http: //www. vip-express. ru/gallery/angar_galery. html

Резервуары воздуховоды шаровый http: //www. ua. allbiz. info/buy/goods/? group=1000551&cid=210891 каплевидный http: //www. ua. allbiz. info/regions/index. php? fuseaction=adm_en terprises. catalog. Products&rgn_id=14&cs=50& page=3 http: //www. tctena. ru/catalog. php? comp_id=10
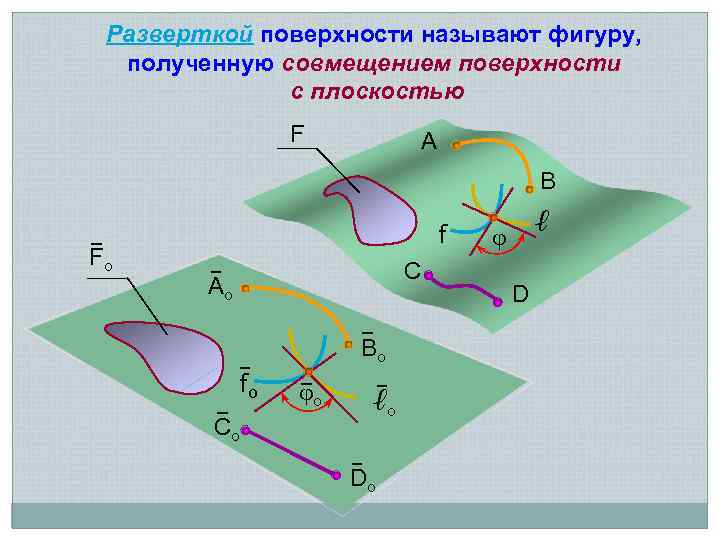
Разверткой поверхности называют фигуру, полученную совмещением поверхности с плоскостью F A B Fо f C Ao Bo fo Co о ℓo Do ℓ D

Основные свойства разверток 1. Длины линий на поверхности и на развертке одинаковы 2. Углы между обыкновенными линиями на поверхности равны соответствующим углам на развертке Углом между линиями называют угол, образованный их касательными, проведенными в точке пересечения линий Преобразование, в котором сохраняется равенство углов называется конформным Поэтому поверхность и развертка конформны

3. Прямые, параллельные на поверхности, остаются параллельными и на развертке Это вытекает из второго свойства 4. Площади, ограниченные замкнутой линией на поверхности и на развертке равны Преобразование, в котором сохраняется равенство площадей, называют эквиареальным

5. Прямая линия на поверхности переходит в прямую линию на развертке 6. Прямая линия между двумя точками на развертке соответствует кратчайшему расстоянию между этими точками на поверхности Эти линии на поверхности называют геодезическими линиями Поверхности, для которых сохраняются указанные свойства на развертке, называют развертывающимися

К числу развертывающихся поверхностей относятся многогранные поверхности; из линейчатых – цилиндрические, конические, торсовые

По возможностям и способам построения различают развертки точные, приближенные и условные Точными называют развертки, построенные с применением математического аппарата, и развертки многогранных поверхностей Приближенными – развертки, построенные способом вписанных или описанных многогранных поверхностей Условные развертки неразвертывающихся поверхностей строят способом цилиндров и конусов
![Точные развертки D =180 – [град] ℓ S 2 A 2 ℓ A 0 Точные развертки D =180 – [град] ℓ S 2 A 2 ℓ A 0](https://present5.com/presentation/3/-29990566_18473900.pdf-img/-29990566_18473900.pdf-85.jpg)
Точные развертки D =180 – [град] ℓ S 2 A 2 ℓ A 0 B 2 B 1 S 1 A 1 S 0 A 0 B 0
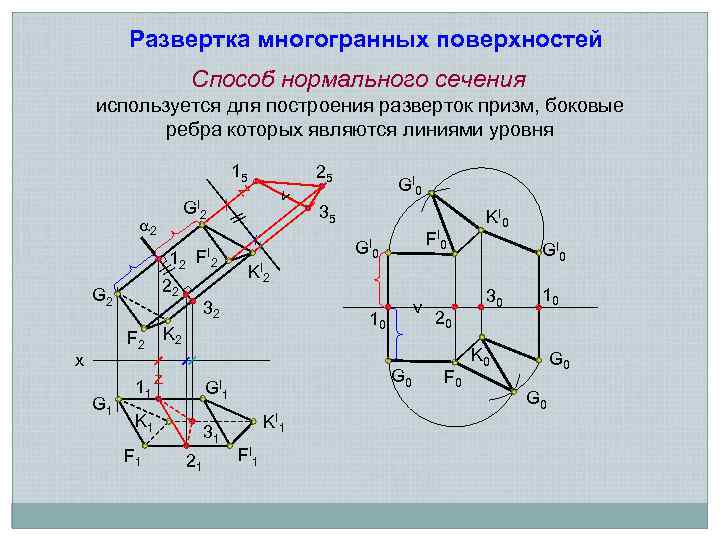
Развертка многогранных поверхностей Способ нормального сечения используется для построения разверток призм, боковые ребра которых являются линиями уровня 15 25 F 2 x G 1 11 I // 12 F 2 22 32 K 2 z F 1 31 21 FI 0 GI 0 KI 2 10 G 0 GI 1 K 1 35 < G 2 // 2 < z GI 2 GI 0 KI 1 FI 1 20 F 0 30 10 K 0 G 0

Приближенные развертки Способ треугольников (триангуляции) Сущность способа заключается в том, что кривую линейчатую поверхность заменяют вписанной в нее многогранной поверхностью с треугольными гранями, нахождению натурального вида многогранной поверхности и последовательному построению на чертеже
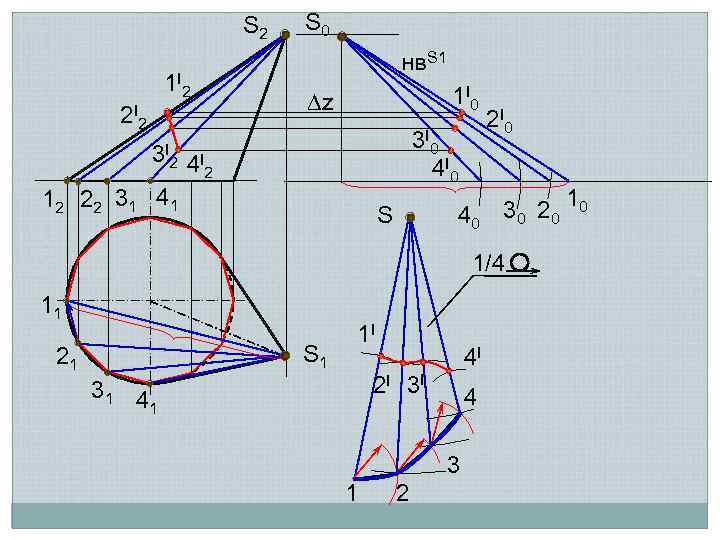
S 2 1 I 2 2 I 2 3 I 2 S 0 нв. S 1 1 I 0 z 3 I 0 4 I 2 12 22 31 41 S 40 2 I 0 30 20 10 1/4 11 S 1 21 1 I 4 I 2 I 3 I 31 4 3 1 2

Условная развертка на основе аппроксимации цилиндрическими или коническими поверхностями
Условная развертка коническими поверхностями
Условная развертка цилиндрическими поверхностями
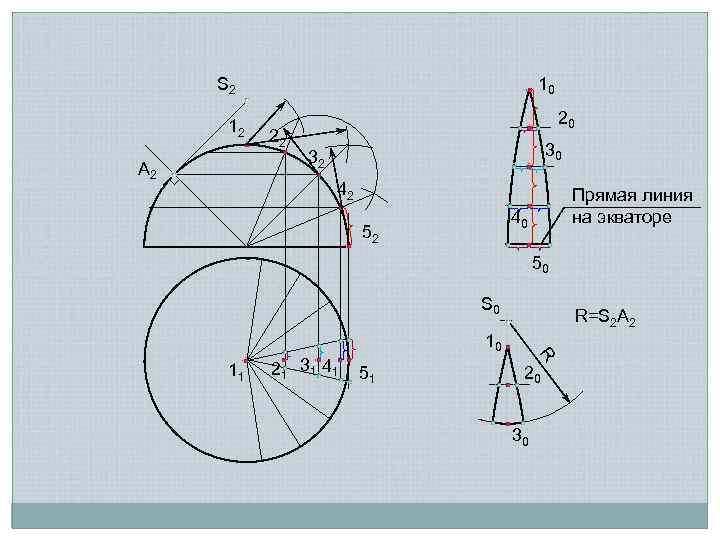
S 2 12 A 2 10 22 20 30 32 42 Прямая линия на экваторе 40 52 50 S 0 R=S 2 A 2 11 21 31 41 51 R 10 20 30

ПОВЕРХНОСТИ

Определение и задание на чертеже Определение Поверхность – совокупность всех последовательных Поверхность положений движущейся линии (образующей) в пространстве (кинематическая поверхность) Способы задания 1. Кинематический – как след движущейся линии 2. Аналитический – как множество точек, удовлетворяющих функционалу: F(x, y, z) 3. Каркасный – семейством линий, принадлежащих поверхности

Задание поверхности на комплексном чертеже 1. Определителем – совокупность геометрических элементов, позволяющих реализовать закон образования поверхности 2. Каркасом – семейством линий 3. Очерком – проекцией контурной линии поверхности
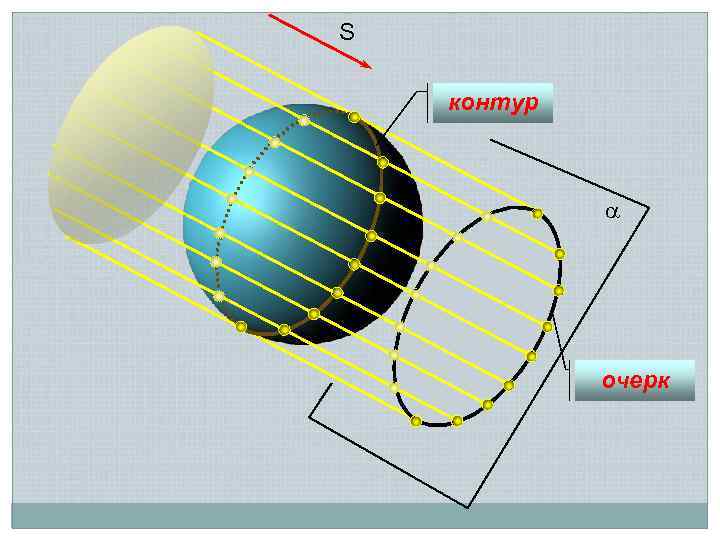
S контур очерк

Линейчатые поверхности Образование поверхностей

Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим

Цилиндрическая поверхность S // ℓ // m ∆(m; ℓ S) Цилиндрическая поверхность образуется движением прямой ℓ (образующей) по некоторой кривой m параллельно самой себе или имеющей постоянное направление S
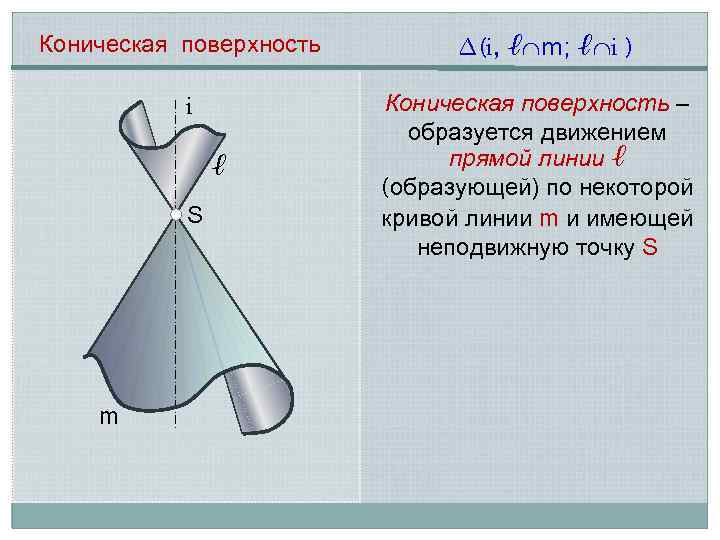
Коническая поверхность i ℓ S m ∆(i, ℓ m; ℓ i ) Коническая поверхность – образуется движением прямой линии ℓ (образующей) по некоторой кривой линии m и имеющей неподвижную точку S
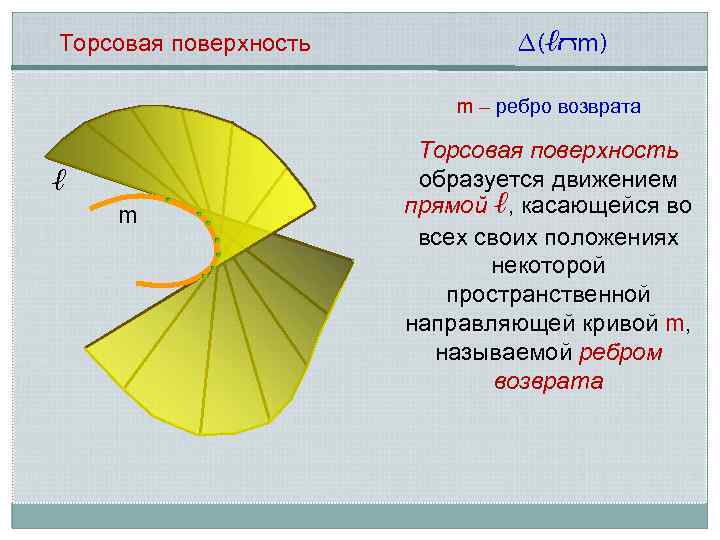
Торсовая поверхность ∆(ℓ m) m – ребро возврата ℓ m Торсовая поверхность образуется движением прямой ℓ, касающейся во всех своих положениях некоторой пространственной направляющей кривой m, называемой ребром возврата
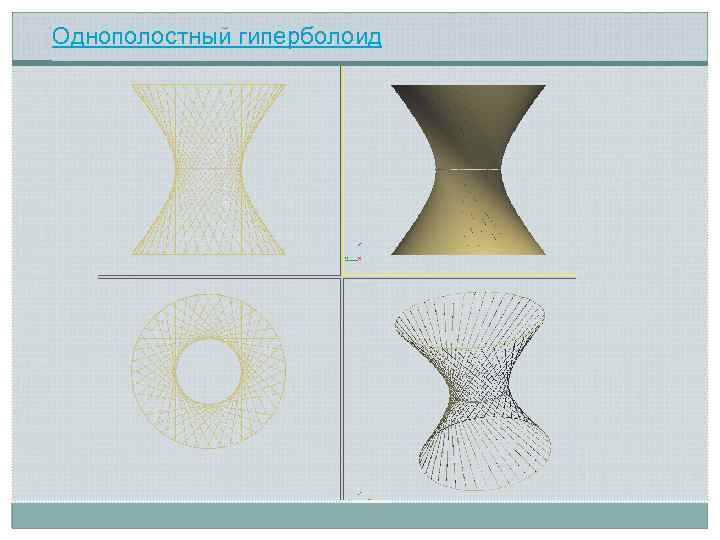
Однополостный гиперболоид

Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников Отсеки плоскостей называются гранями, а линии их пересечения – ребрами Точки пересечения ребер называются вершинами
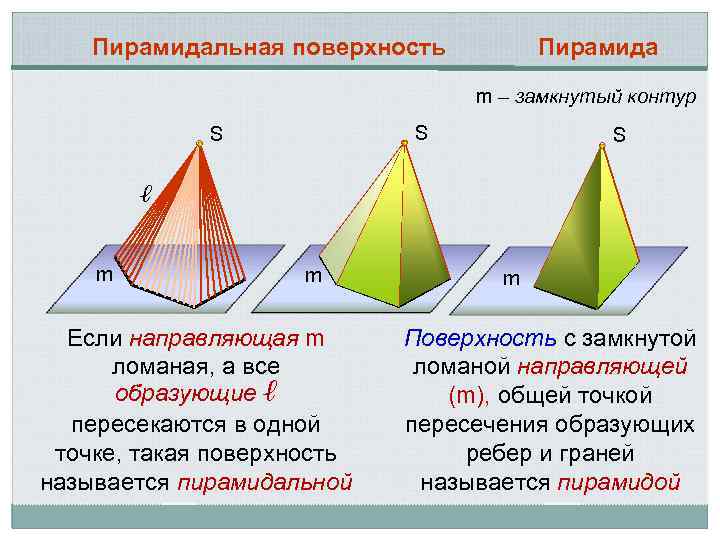
Пирамидальная поверхность Пирамида m – замкнутый контур S S S ℓ m m Если направляющая m ломаная, а все образующие ℓ пересекаются в одной точке, такая поверхность называется пирамидальной m Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой

Принадлежность точки поверхности
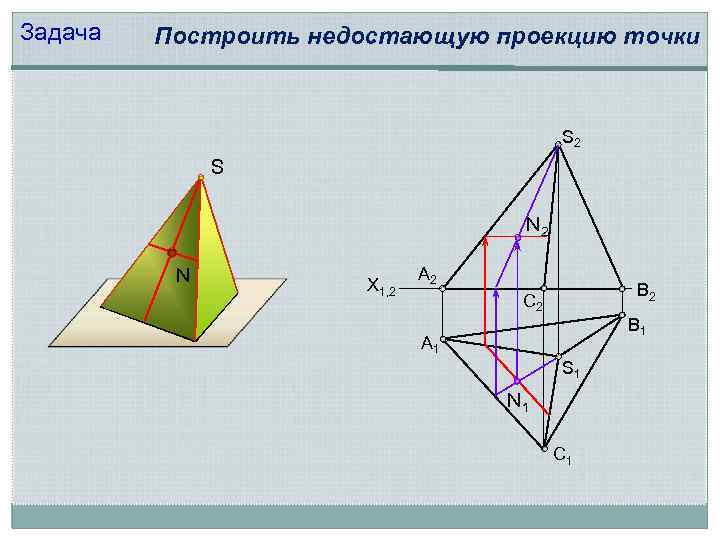
Задача Построить недостающую проекцию точки S 2 S N 2 N X 1, 2 А 2 В 2 С 2 В 1 А 1 S 1 N 1 С 1
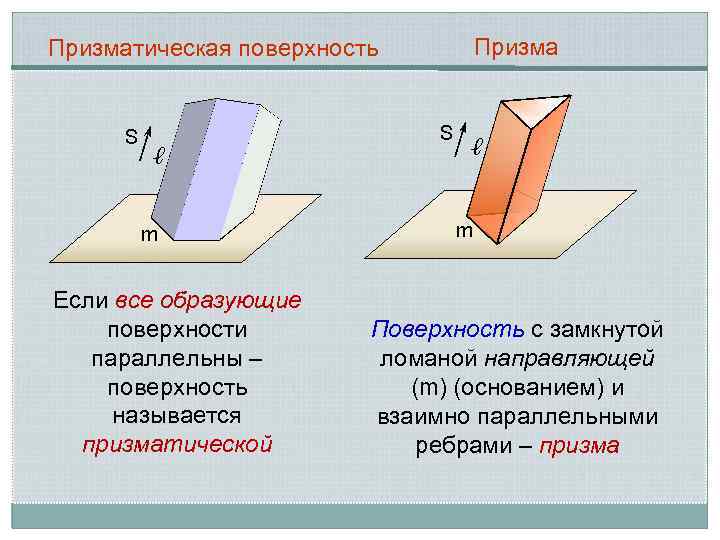
Призматическая поверхность S ℓ m Если все образующие поверхности параллельны – поверхность называется призматической S ℓ m Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами – призма
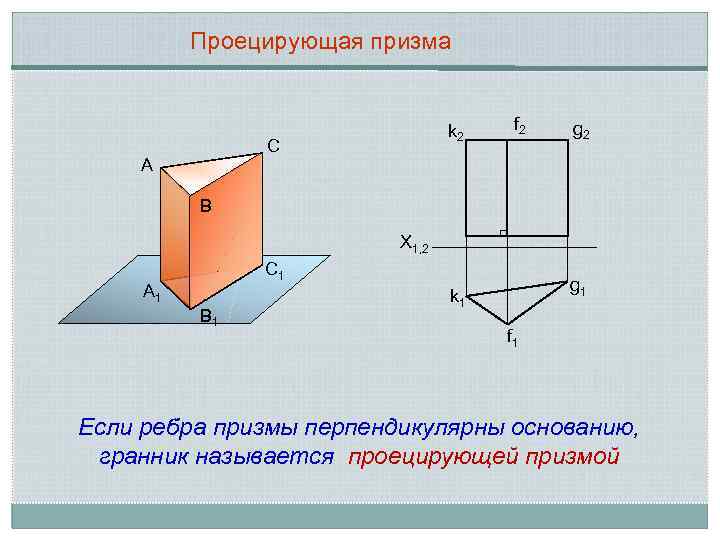
Проецирующая призма k 2 С А f 2 g 2 В X 1, 2 С 1 А 1 В 1 g 1 k 1 f 1 Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой

Поверхности Каталана
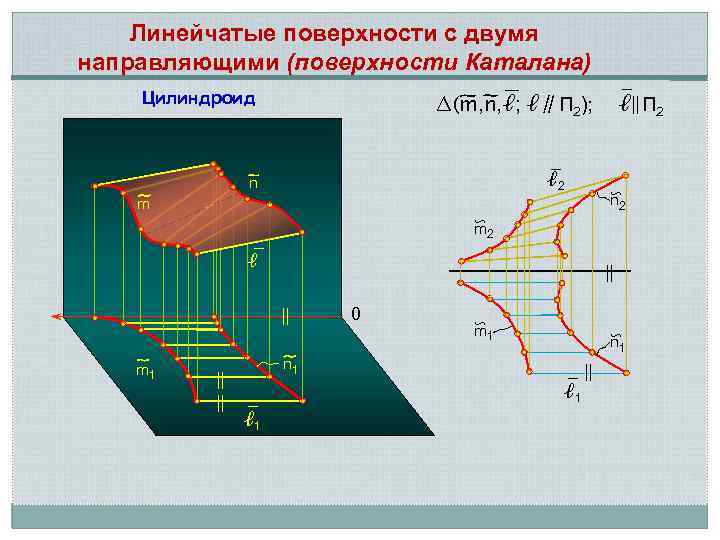
Линейчатые поверхности с двумя направляющими (поверхности Каталана) Цилиндроид ∆(m, n, ℓ; ℓ∥П 2); ℓ 2 n m ∽ n 2 ∽ m 2 ℓ ∥ ∥ m 1 ∥ ∥ 0 ∽ m 1 ∽ n 1 ℓ 1 ℓ∥П 2 ∥

Гипар Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом, или косой плоскостью
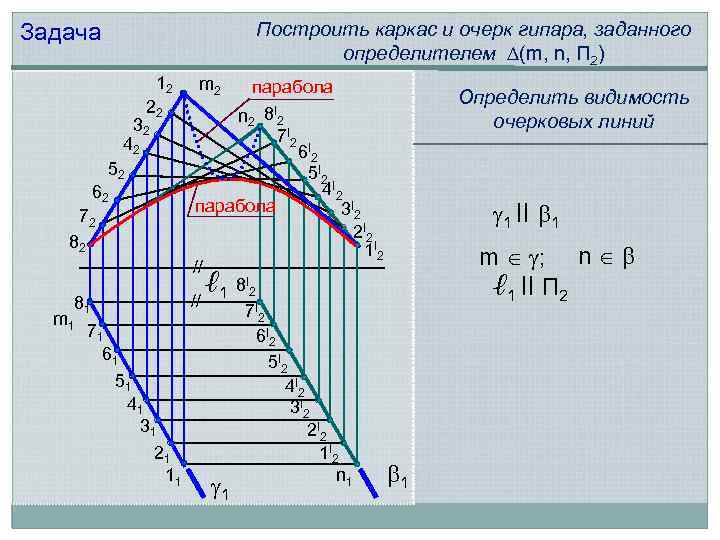
Построить каркас и очерк гипара, заданного определителем (m, n, П 2) Задача 12 22 m 2 парабола n 2 8 I 2 32 7 I 2 42 6 I 2 52 5 I 2 4 I 2 62 парабола 3 I 2 72 2 I 2 82 1 I 2 // ℓ 1 8 I 2 // 81 7 I 2 m 1 71 6 I 2 61 5 I 2 51 4 I 2 41 3 I 2 31 2 I 2 21 1 I 2 11 n 1 1 1 Определить видимость очерковых линий 1 ll 1 m ; n ℓ 1 ll П 2

Винтовая поверхность Винтовой поверхностью называют поверхность, образованную винтовым движением образующей Винтовым движением называют движение, при котором каждая точка А образующей вращается вокруг неподвижной оси i и одновременно перемещается поступательно вдоль этой оси
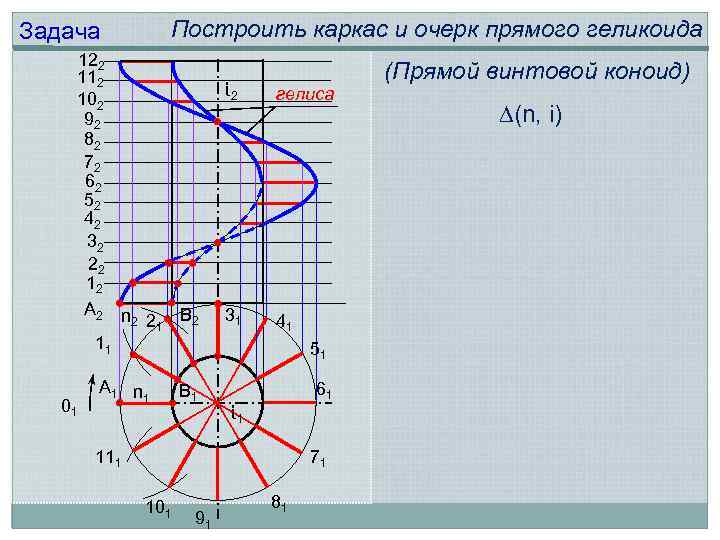
Построить каркас и очерк прямого геликоида Задача 122 112 102 92 82 72 62 52 42 32 22 12 А 2 n 2 21 В 2 11 01 А 1 n 1 В 1 ί 2 гелиса 31 41 51 61 ί 1 111 71 101 91 81 (Прямой винтовой коноид) (n, i)
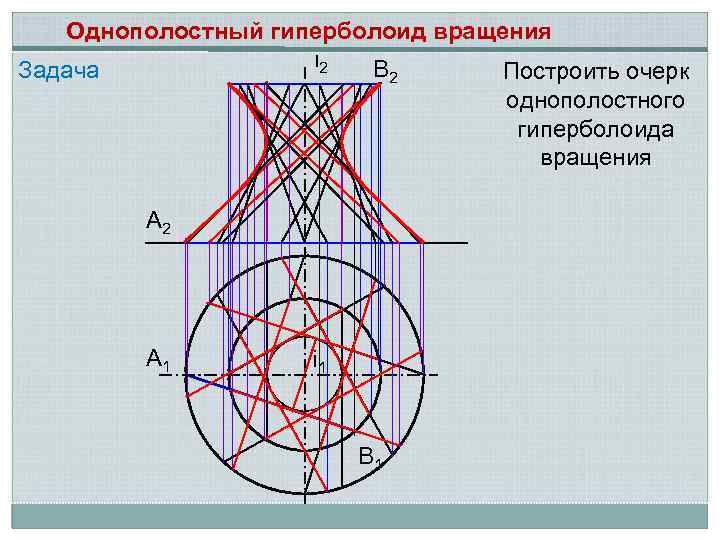
Однополостный гиперболоид вращения i 2 В 2 Задача Построить очерк однополостного гиперболоида вращения А 2 А 1 i 1 В 1

Поверхности вращения

Поверхность α , образованная вращением образующей ℓ вокруг неподвижной оси i, называется поверхностью вращения
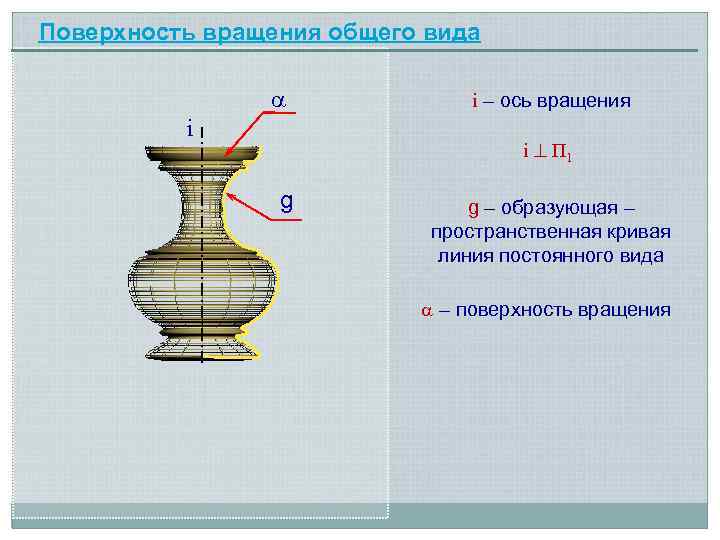
Поверхность вращения общего вида i i – ось вращения i П 1 g g – образующая – пространственная кривая линия постоянного вида – поверхность вращения
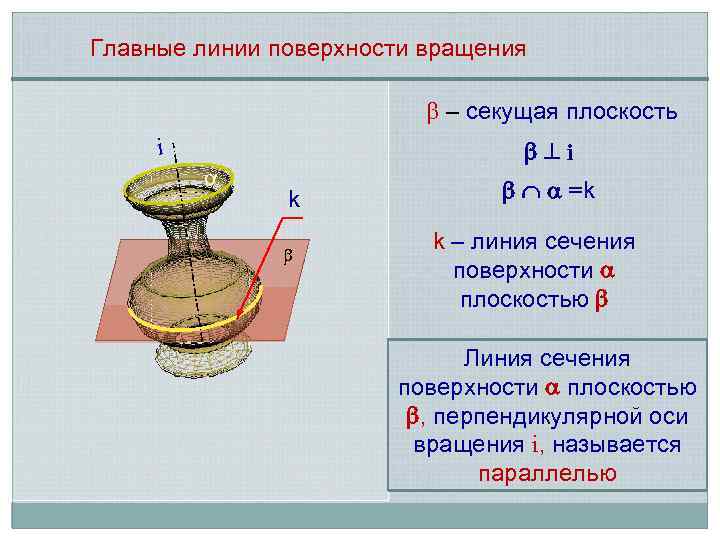
Главные линии поверхности вращения – секущая плоскость i i k =k k – линия сечения поверхности плоскостью Линия сечения поверхности плоскостью , перпендикулярной оси вращения i, называется параллелью
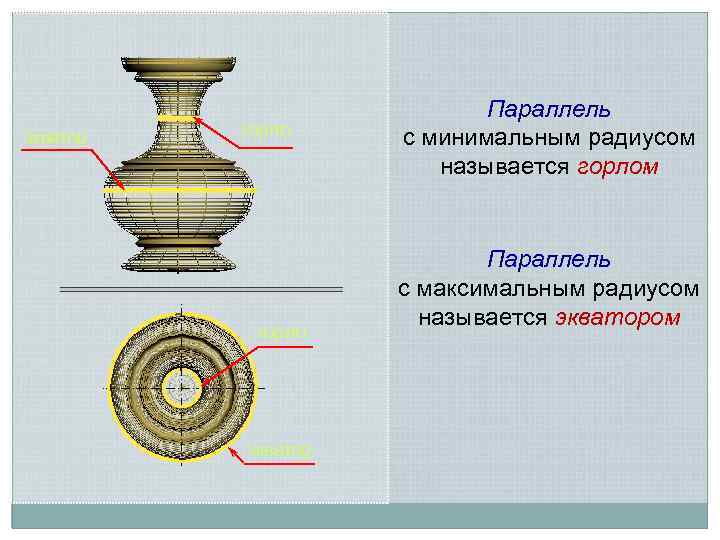
экватор горло экватор Параллель с минимальным радиусом называется горлом Параллель с максимальным радиусом называется экватором

i λ – секущая плоскость λ∈i λ =m λ m m – линия сечения поверхности плоскостью λ Линия сечения поверхности плоскостью λ, проходящей через ось вращения i, называется меридианом (случайным меридианом)
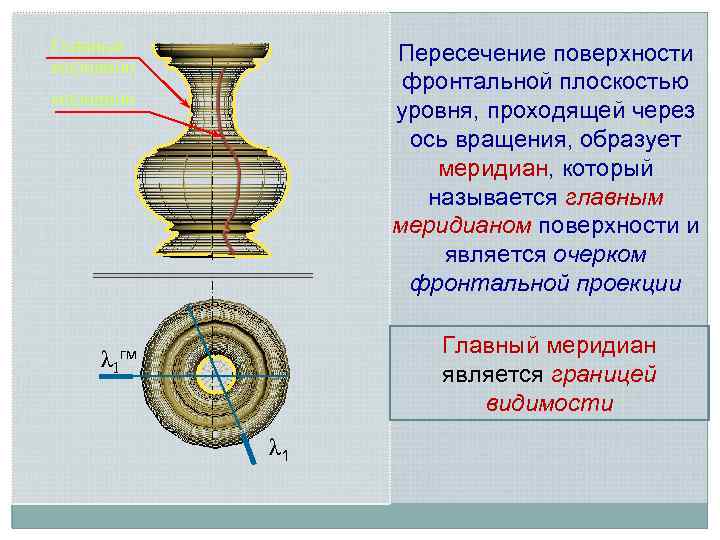
Главный меридиан Пересечение поверхности фронтальной плоскостью уровня, проходящей через ось вращения, образует меридиан, который называется главным меридианом поверхности и является очерком фронтальной проекции меридиан Главный меридиан является границей видимости λ 1 гм λ 1
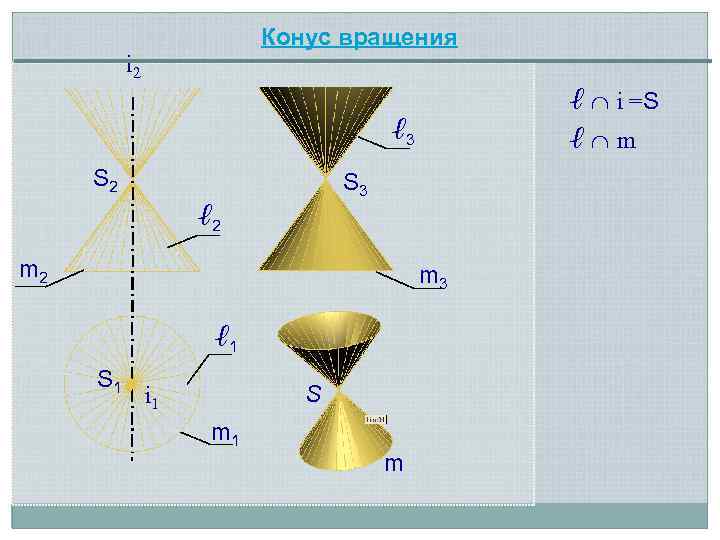
Конус вращения i 2 ℓ i =S ℓ 3 S 2 ℓ m S 3 ℓ 2 m 3 ℓ 1 S i 1 m

Принадлежность точки поверхности

Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности

Среди точек кривой выделяют опорные точки: – экстремальные точки – высшая и низшая, крайняя левая и крайняя правая, самая далекая и самая ближняя точки кривой; – граничные точки видимости кривой, принадлежащей поверхности, лежат на очерках поверхности и отделяют видимую часть поверхности от ее невидимой части
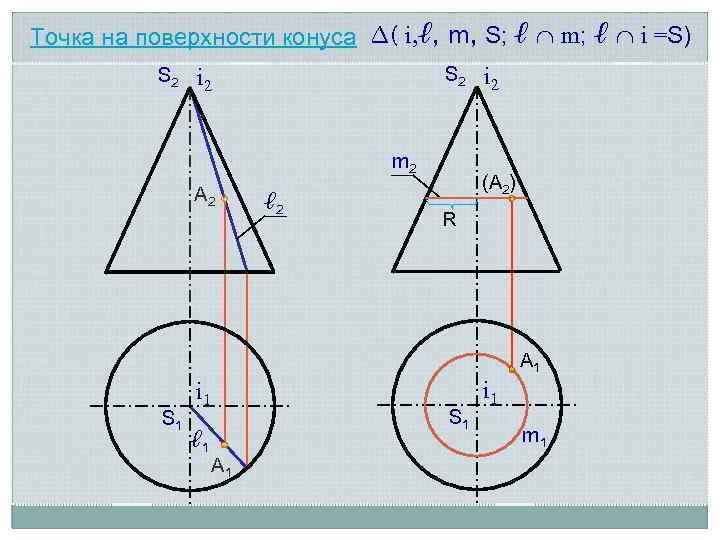
Точка на поверхности конуса ∆( i, ℓ, m, S; ℓ m; ℓ i =S) S 2 i 2 m 2 А 2 ℓ 2 i 2 (А 2) R А 1 S 1 i 1 ℓ 1 S 1 А 1 i 1 m 1

Вогнутый тор (глобоид) Поверхность, образованная внутренней стороной вращающейся дуги радиусом R, называется глобоидом
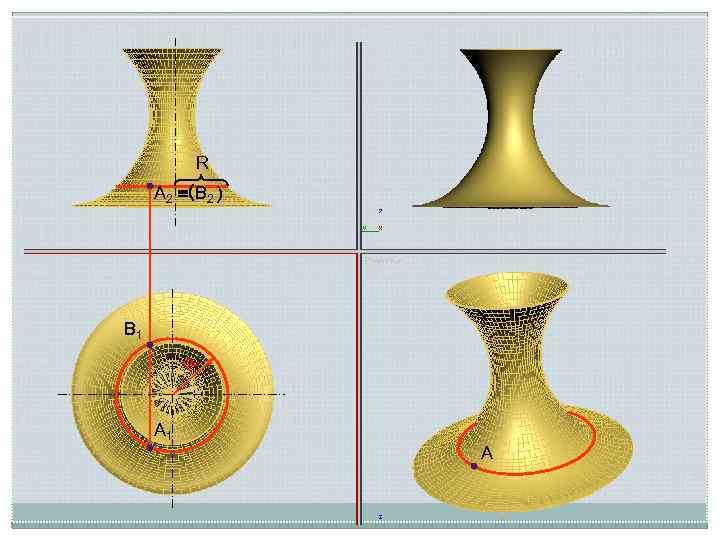
R А 2 (В 2 ) В 1 R А 1 А
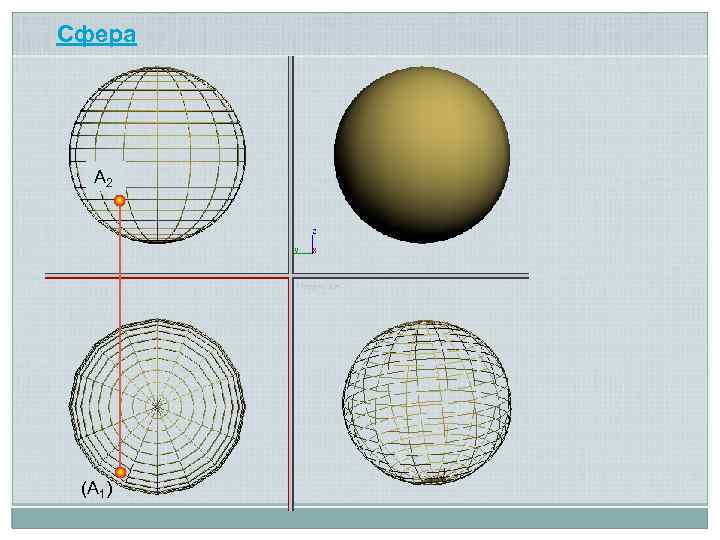
Сфера A 2 (A 1)

Выпуклый тор i 2 А 2 (В 2) R С 2 (D 2) R (D 1) В 1 R (C 1) А 1
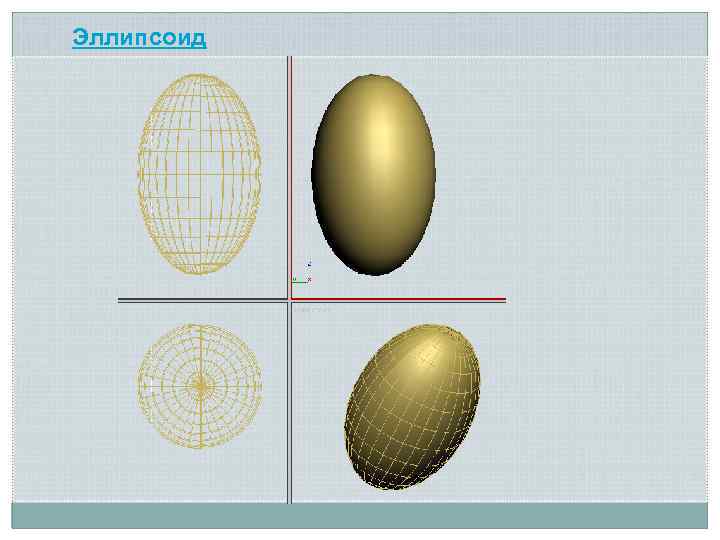
Эллипсоид
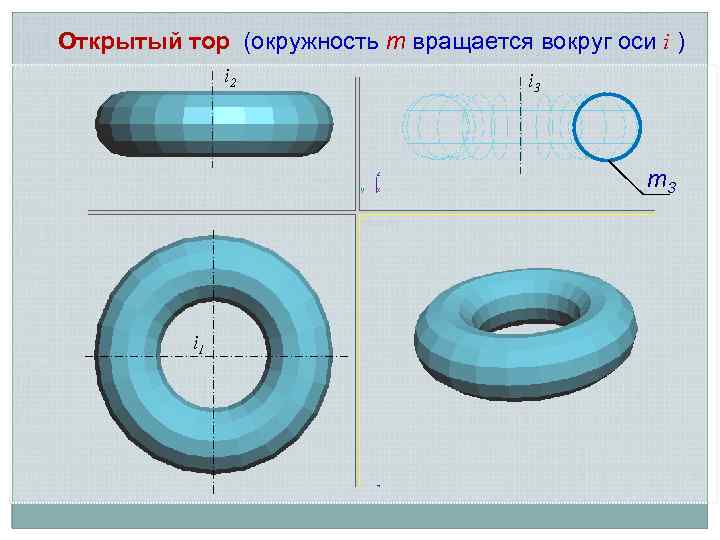
Открытый тор (окружность m вращается вокруг оси i ) i 2 i 3 m 3 i 1
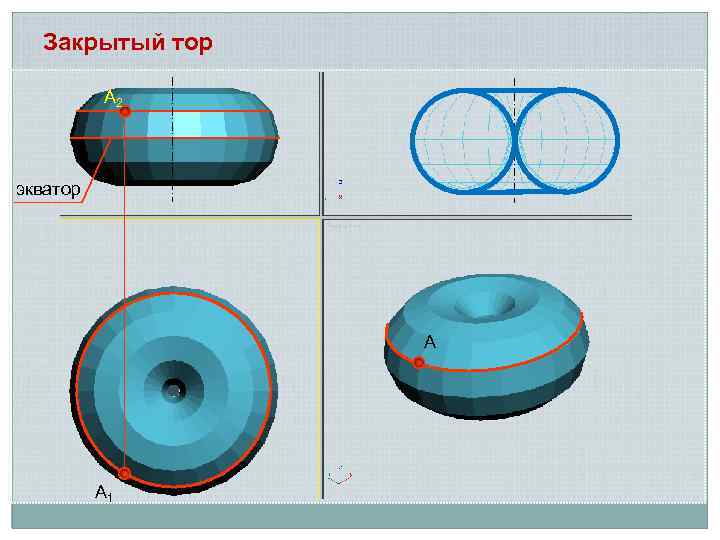
Закрытый тор А 2 экватор А А 1

Закрытый кольцевой тор (самопересекающийся)
Адонкина, Поверхности.ppt