Лекция 4_5_Классификация и моделирование биотехнических систем.pptx
- Количество слайдов: 50

КЛАССИФИКАЦИЯ БИОТЕХНИЧЕСКИХ СИСТЕМ Биотехнические системы и технологии

КЛАССИФИКАЦИЯ БТС По характеру основной целевой функции БТС разделены на 3 группы: Ø- БТС медицинского назначения (БТС – М); Ø- БТС эргатического типа (БТС – Э) с человеком – оператором в качестве управляющего звена; Ø- БТС целенаправленного управления поведением целостного организма (БТС – У). В настоящее время к этим группам дополнительно относятся: ØБТС лабораторного анализа (БТС-ЛА); ØМониторные системы (МС); ØБТС искусственного жизнеобеспечения.

БТС МЕДИЦИНСКОГО НАЗНАЧЕНИЯ (БТС – М) q. БТС-М предназначены для использования в медицинских целях, главным из которых являются: ØДиагностика состояния живого организма (текущая), проводимая в реальном масштабе времени, и дифференциальная, осуществляемая в процессе апостериорной медико-биологической информации. ØУправление состоянием организма для его нормализации (методами дискретной или непрерывной коррекции). Ø Временная или длительная компенсация утраченных функций органов или физиологических систем живого организма. ØПротезирование и коррекция функций сенсорных систем или двигательного аппарата. ØРазличные медико-биологические исследования и лечебные процедуры, связанные с применением приборов активного вмешательства, сочлененных с живым организмом в единую БТС.

БТС МЕДИЦИНСКОГО НАЗНАЧЕНИЯ (БТС – М) q. Вся медико-биологическая информация разделяется на медленно изменяющиеся процессы (МИП) и быстроизменяющиеся процессы (БИП). При этом к МИП относят процессы, частота изменения которых ниже 1 Гц, а мгновенные значения могут быть выражены цифрой. Пример: üчастота сердечных сокращений; üчастота дыхания; üтемпература тела и др. q. К БИП относятся, главным образом, электрофизические процессы, характеризуемые изменением электрических потенциалов на поверхности кожи или на отдельных локальных участках организма под ее покровами. Пример: üэлектрокардиосигнал (ЭКС) (ЭКГ); üэлектроэнцефалограмма (ЭЭГ); üэлектромиограмма (ЭМГ) и др. q. Частотные спектры БИП находятся в диапазоне 0, 1… 1000 Гц.
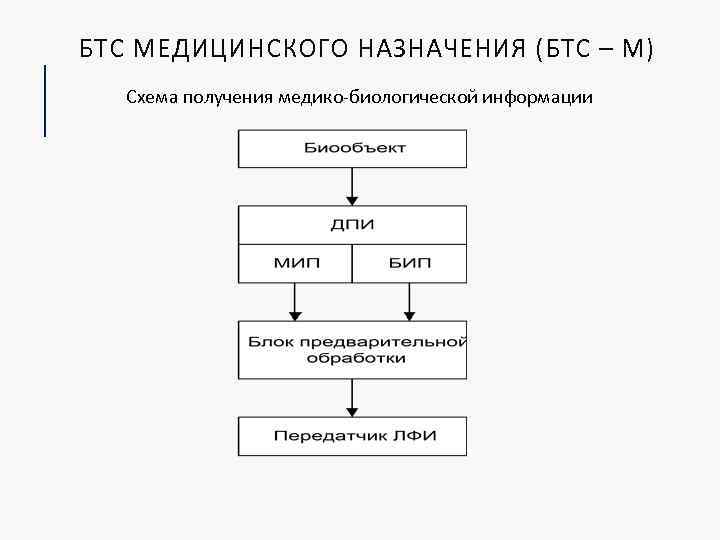
БТС МЕДИЦИНСКОГО НАЗНАЧЕНИЯ (БТС – М) Схема получения медико-биологической информации
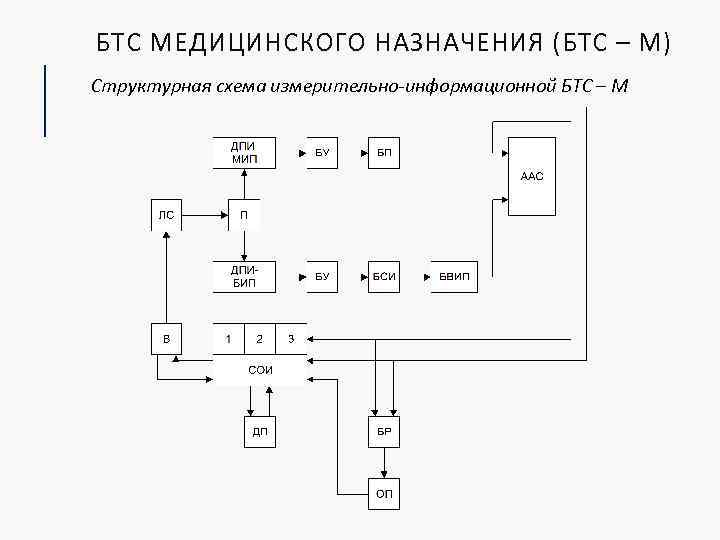
БТС МЕДИЦИНСКОГО НАЗНАЧЕНИЯ (БТС – М) Структурная схема измерительно-информационной БТС – М

БИОТЕХНИЧЕСКИЕ СИСТЕМЫ ЭРГАТИЧЕСКОГО ТИПА (БТС – Э) q. В подобных системах (БТС – Э) или (по общепринятой терминологии) в системах “человек-машина” биологическое звено представлено человеком-оператором, выполняющим различные функции в замкнутом контуре управления технической системой. q. В процессе анализа и синтеза БТС – Э практически приходится иметь дело с моделированием на четырех уровнях: Øтканевом (в случае моделирования процессов метаболизма при определении энергозатрат организма человека в процессе деятельности); Øорганном (при бионических исследованиях органов восприятия для оптимального сопряжения их с техническими элементами информационных каналов); Øорганизменном (при исследовании поведения оператора в процессе управления динамическими процессами); Øпопуляционном (про разработке методов управления популяцией живых организмов с целью организации их целенаправленного поведения).

БИОТЕХНИЧЕСКИЕ СИСТЕМЫ ЭРГАТИЧЕСКОГО ТИПА (БТС – Э) q Техническая реализация метода поэтапного моделирования воплощается в тренажерно – моделирующем комплексе (ТМК). ТМК является многоцелевой универсальной системой, предназначенной для: Ø учета человеческого фактора на ранних стадиях синтеза БТС – Э; Ø оптимизация режима работы оператора, выработки количественных оценок эффективности их деятельности на пультах управления различных конструкций и разработки инженерных рекомендаций по усовершенствованию существующих систем управления эргатического типа; Ø получение априорной информации с целью обоснования модели идеального оператора применительно к системе данного типа; Ø разработки методик профотбора, обучения и тренировок операторов, а так же для подготовки операторов методов стадийной тренировки; Ø тренировки операторов комплексов и систем в период их разработки задолго до их воплощения в действующие – конструкции.
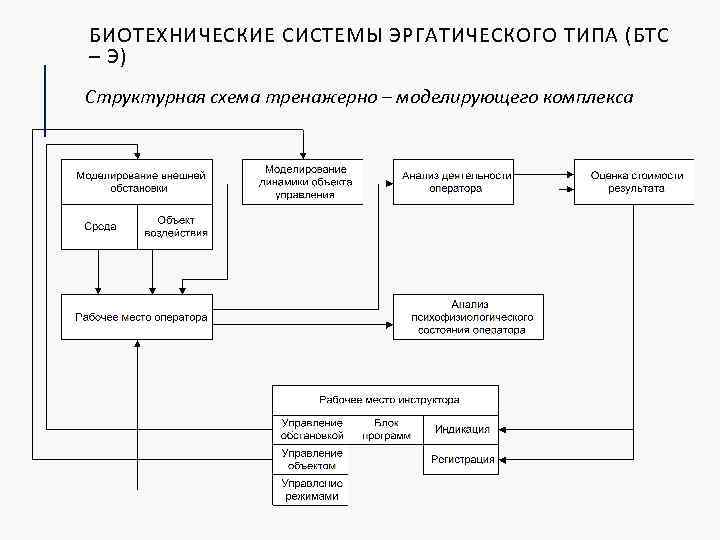
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ ЭРГАТИЧЕСКОГО ТИПА (БТС – Э) Структурная схема тренажерно – моделирующего комплекса
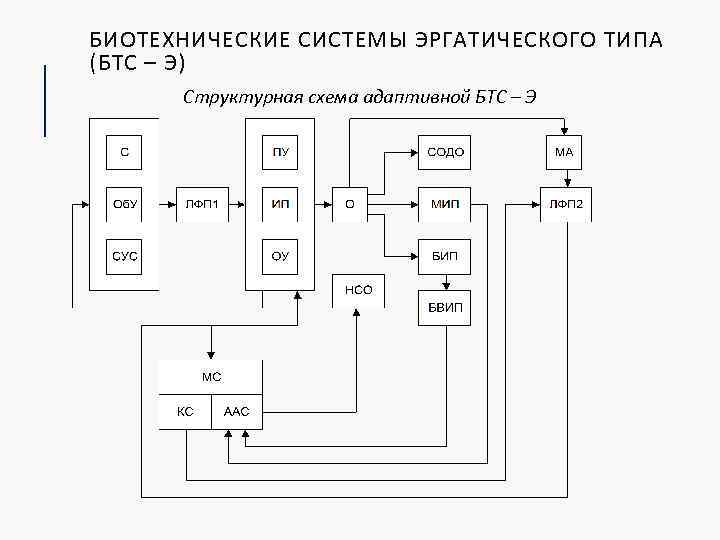
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ ЭРГАТИЧЕСКОГО ТИПА (БТС – Э) Структурная схема адаптивной БТС – Э
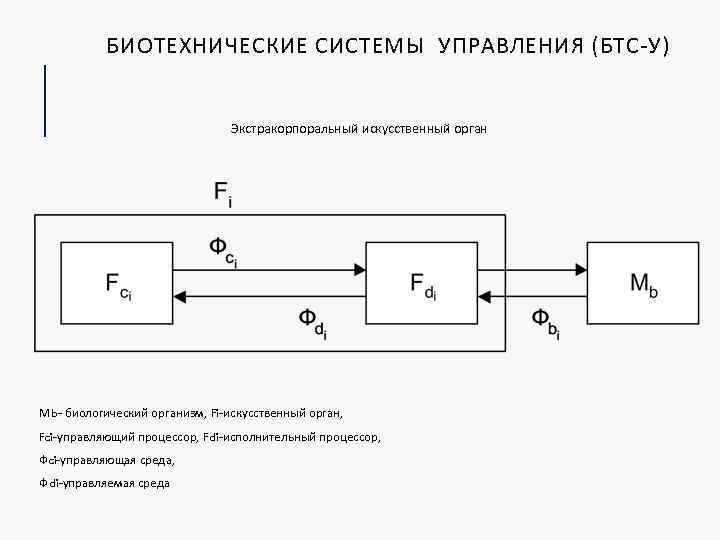
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (БТС-У) Экстракорпоральный искусственный орган Мb- биологический организм, Fi-искусственный орган, Fci-управляющий процессор, Fdi-исполнительный процессор, Фci-управляющая среда, Фdi-управляемая среда
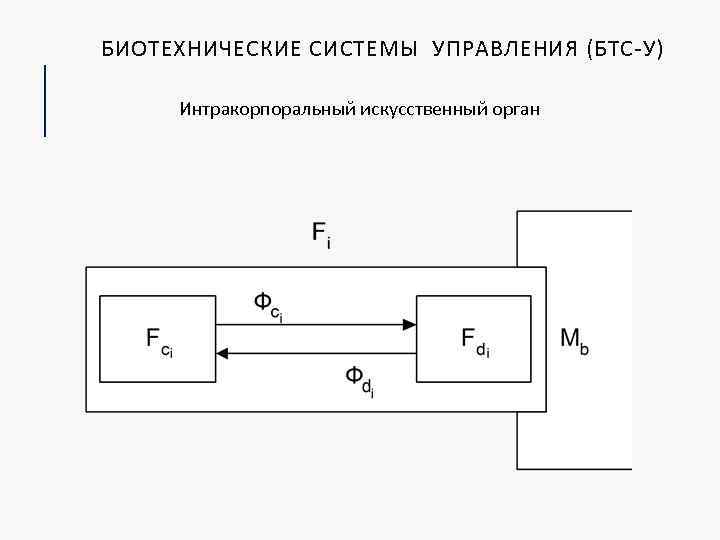
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (БТС-У) Интракорпоральный искусственный орган
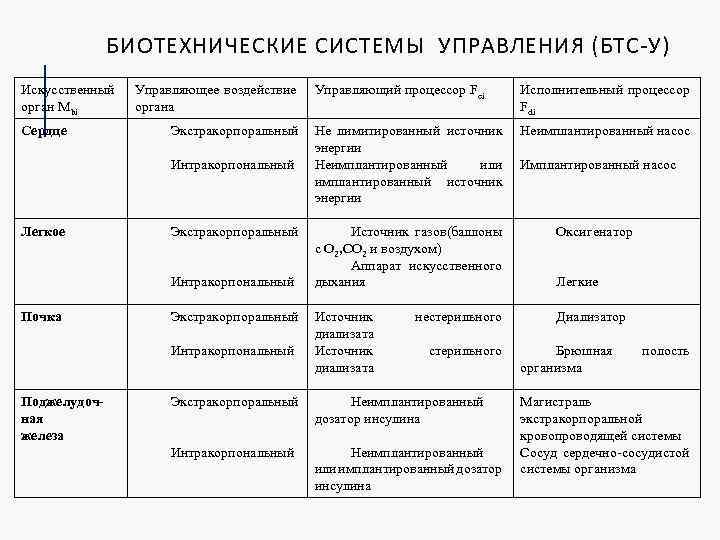
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (БТС-У) Искусственный орган Mbi Сердце Управляющее воздействие органа Экстракорпоральный Интракорпональный Легкое Экстракорпоральный Интракорпональный Почка Экстракорпоральный Интракорпональный Поджелудочная железа Управляющий процессор Fci Исполнительный процессор Fdi Не лимитированный источник энергии Неимплантированный или имплантированный источник энергии Неимплантированный насос Источник газов(баллоны с О 2, СО 2 и воздухом) Аппарат искусственного дыхания Оксигенатор Источник диализата Диализатор нестерильного Экстракорпоральный Неимплантированный дозатор инсулина Интракорпональный Неимплантированный или имплантированный дозатор инсулина Легкие Брюшная организма полость Магистраль экстракорпоральной кровопроводящей системы Сосуд сердечно-сосудистой системы организма
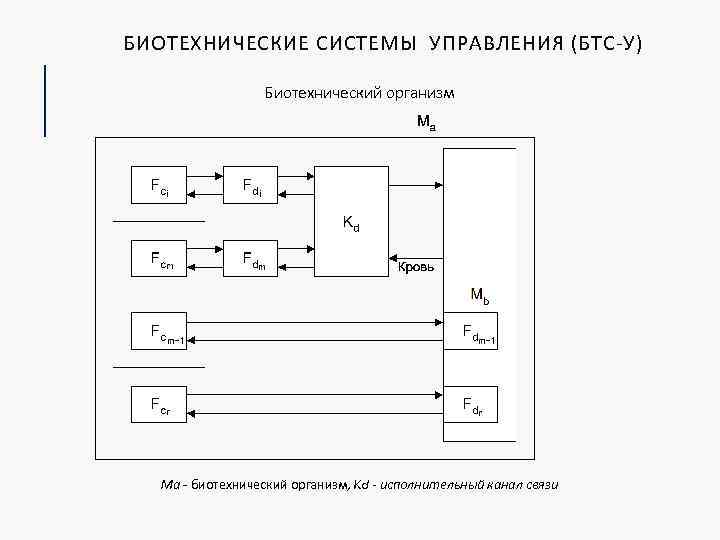
БИОТЕХНИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (БТС-У) Биотехнический организм Ма - биотехнический организм, Kd - исполнительный канал связи

ПРИНЦИПЫ СИНТЕЗА И МОДЕЛИРОВАНИЯ БИОТЕХНИЧЕСКИХ СИСТЕМ Биотехнические системы и технологии

ПРИНЦИПЫ СИНТЕЗА БИОТЕХНИЧЕСКИХ СИСТЕМ Определение и общие свойства БТС q. Биотехническая система (БТС) представляет собой совокупность биологических и технических элементов, объединенных в единую функциональную систему целенаправленного поведения. q. Основным свойством БТС является суперадаптивность, обусловленная наличием двух контуров адаптации - внешнего и внутреннего. q. Внешний контур обеспечивает БТС возможность выполнять свою целевую функцию в условиях переменных воздействий внешних факторов. q Внутренний контур (или многие контуры) позволяет элементам БТС взаимно адаптироваться к изменению состояния друга, вызванного воздействием внешних или внутренних факторов. q. Т. о. , в БТС наличие биологических звеньев позволяет придать общим свойствам системы особую пластичность, улучшить адаптивные характеристики во внешнем контуре адаптации (особенно в системах типа "человек" - "машина" - "окружающая среда").

ПРИНЦИПЫ СИНТЕЗА БИОТЕХНИЧЕСКИХ СИСТЕМ Основные принципы сопряжения технических и биологических элементов 1. Принцип адекватности, требующий согласования основных конструктивных параметров и "управленческих характеристик" биологических и технических элементов БТС. 2. Принцип единства информационной среды, требующий согласования свойств информационных потоков, циркулирующих между техническими и биологическими элементами как в афферентных, так и в эффекторных цепях БТС.

ПРИНЦИПЫ СИНТЕЗА БИОТЕХНИЧЕСКИХ СИСТЕМ Принципы бионического подхода 1. При построении структурно-функциональной схемы БТС используется принцип обработки основных потоков информации специализированными периферическими системами. 2. Периферические системы могут "очувствляться", а информация может перераспределяться по различным сенсорным воспринимающим входам. 3. Основные элементы системы обмениваются информацией, что позволяет осуществлять процедуры внешней и внутренней адаптации. 4. Используется свойственный живым организмам принцип качественных оценок ситуации с последующим уточнением с помощью относительных измерений и сравнение с выбранным эталонным порогом. 5. Вводится специальный контур системы регенерации (контур нормализации состояния оператора), управляемый системой текущей диагностики.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Общие вопросы теории моделирования БТС q. В области естественных наук наиболее распространенными являются два вида моделирования: Øфизическое; Øматематическое. q. Процесс физического моделирования состоит в изучении посредством анализа некоторого макета, сохраняющего физическую природу системы. üПример: модель метательного аппарата, исследуемая в аэродинамической трубе, искусственное сердце, искусственные легкие и т. д. q. Модели физического типа имеют органическую сферу применения, т. к. не для всяких явлений и объектов могут быть построены физические аналоги. Это привело к распространению математического моделирования объектов и процессов. Динамика функционирования различных по физической природе систем зачастую описывается однотипными математическими зависимостями. q. Математическую модель строят на основе законов и закономерностей, выявленных фундаментальными науками. üПример: одними и теми же уравнениями может быть описан электрический колебательный контур и пружинный маятник. Математическое моделирование основано на том факте, что различные изучаемые явления могут иметь одинаковое математическое описание.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Классификация математических моделей q. Одномерные вероятностные модели : параметрические; непараметрические. ØПри построении параметрической модели распределение случайных величин аппроксимируется известным вероятными законами распределения (чаще всего нормальным законом). üПример: когда в справочнике указано, что у здорового человека в состоянии покоя объем вдыхаемого воздуха составляет 400 -800 мл, это значит, что распределение величины объема моделируются равномерным законом. ØНепараметрическими моделями называются те, у которых закон распределения случайных величин неизвестен. q. Многомерные вероятностные модели ØПредставляют собой многомерные описания состояния биотехнических систем и процессов в них протекающих, к признакам этих систем относят существенные параметры, характеризующие определенные единицы наблюдения. ØДвухмерное пространство признаков, образованное двумя переменными, содержит скопление точек на плоскости. ØТрехмерное пространство, образованное тремя переменными содержит облака точек наблюдений. üПример: геометрические размеры и биохимические характеристики клетки, интервалы между зубцами ЭКГ и т. д.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Детерминированные модели q с непрерывным пространством и временем представляют собой функциональные или аналитические зависимости. Эти модели чаще всего отображают процессы, а не состояния. üПример: в фармакологии при описании зависимости "дозаэффект" при описании физиологических процессов: обмена веществ, роста и развития и т. п. q с дискретным пространством и временем (так называется логические). Используются при решении ряда комбинаторных задач.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Модели процессов управления q. Управления в БТС может осуществляться с использованием обратной связи и без нее. В соответствие с этим модели процессов управления могут быть разделены на группы: Ø- модели с незамкнутыми контурами; Ø- модели с замкнутыми контурами. q. В модели с незамкнутыми контурами отсутствует ОС, т. е. это открытая система, которой свойственно регулирование по возмущению. При этом учитывается только информация о величине возмущения, но не о результатах регулирования. üПример: использование глюкозы для подкормки организма в период его ослабления. q. В моделях с замкнутыми контурами управления осуществляется регулирование по отклонению, в величине которого за счет обратной связи учитывается информация о результатах регулирования. Это замкнутые системы управления и саморегулирующиеся. üПример; введение лекарственных препаратов, снижающих уровень сахара в крови, больному сахарным диабетом.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Основные этапы моделирования 1. Постановка цели моделирования üДля одной и той же системы можно составить множество моделей. Они будут отличаться степенью детализации и учета тех или иных особенностей системы и режимов ее функционирования. 2. Создание концептуальной модели üКонцептуальная (или содержательная) модель – это словесное описание системы – ее состав и структура, свойства входящие в нее элементов и причинно– следственные связи. 3. Формирование информационного обеспечения модели üПри создании концептуальной модели определяются качественные и количественные параметры БТС и внешних воздействий на нее. К качественным параметрам относят те, которые нельзя оценить в каких- то единицах измерений. Для количественных параметров необходимо определить их конкретные значения, которые будут использованы в виде исходных данных при моделировании. 4. Разработка математической модели 5. Выбор метода моделирования üРазработанная математическая модель может быть исследована различными методами: аналитическими; имитационными.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Основные этапы моделирования 6. Технические средства моделирования 7. Корректировка модели ØПри выявлении недопустимого рассогласования модели и системы возникает необходимость в корректировке модели. При этом могут быть выделены следующие типы изменений: ü глобальные (требуют для устранения разработки новой модели); ü локальные (требуют частичного изменения математической модели); ü параметрические (изменения некоторых параметров (калиброванных). 8. Проверка адекватности модели 9. Планирование экспериментов с моделью Øа) Стратегическое планирование. Øб) Тактическое планирование. 10. Обработка измерений имитационного эксперимента 11. Использование результатов моделирования

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Метод поэтапного моделирования q. Подготовительный (этап 1) üРазрабатывается структурно – функциональная схема БТС, конкретизируются её целевая функция (ЦФ) и возможные режимы работы. Определяется биологический объект и предварительный алгоритм его функционирования в БТС. üНа основании априорных данных создается модель БТС с математической моделью биологического элемента. q. Управленческое согласование характеристик элементов БТС (этап 2) üОсуществляются итерационные процедуры согласования характеристик элементов БТС в едином контуре управления. üПрактическое значение результатов этого этапа заключается в том, что можно отобрать операторов для БТС эргатического типа или подобрать прямой биологический аналог человеческому организму при экспериментах.

ОБЩИЕ ВОПРОСЫ МОДЕЛИРОВАНИЯ В БТС Метод поэтапного моделирования q. Информационное согласование (этап 3) üИсследуются информационные процессы, обеспечивающие соблюдение принципов адекватности и идентификации информационной среды. üКорректируются решающие правила, заложенные в виде программ в системы обработки информации о состоянии биологического объекта; üРазрабатываются специальные требования к техническим устройствам, согласующим информационные и управленческие характеристики технической и биологической частей БТС, получившие названия логических фильтров – преобразователей (ЛФП). q. Заключительный (этап 4) üПроводится исследование БТС в полунатурных (модельных) и натурных условиях. üИдет обработка данных эксперимента и окончательная корректировка математической модели. üПодготавливаются задания на инженерную разработку БТС.

Примеры моделирования БТС

Основные направления математического моделирования гемодинамики Моделирование течения крови в отдельном сосуде 2 D и 3 D модели течения в крупных сосудах (уравнения Навье-Стокса) (моделирование упругости стенки сосуда, турбулентность течения, многокомпонентность крови (не ньютоновская жидкость), взаимодействие со стенками сосуда, области бифуркации сосудов, моделирование тромбообразования, стенозов, аневризмов и т. д. ) 2 D и 3 D модели течения крови в мелких сосудах (капиллярах)с учетом реологии. Моделирование течения крови в сердце (2 D и 3 D модели) Моделирование течения крови в сети сосудов (дерево сосудов, замкнутая система) для исследования общих закономерностей течения крови. - На основе балансных соотношений - На аналогиях с «электрической цепью» - Квазиодномерное приближение: - соответствует типу сосудистой сети - дает возможность описать систему кровообращения в целом - позволяет отслеживать параметры течения крови вдоль сосуда - позволяет учесть особенности каждого сосуда - является основой для построения разномасштабных моделей -предоставляет возможность расчета переноса веществ кровью -предоставляет возможность использовать различные модели сосудов и органов -использует доступные физиологические данные -обладает хорошей точностью -предъявляет разумные требования к вычислительным мощностям
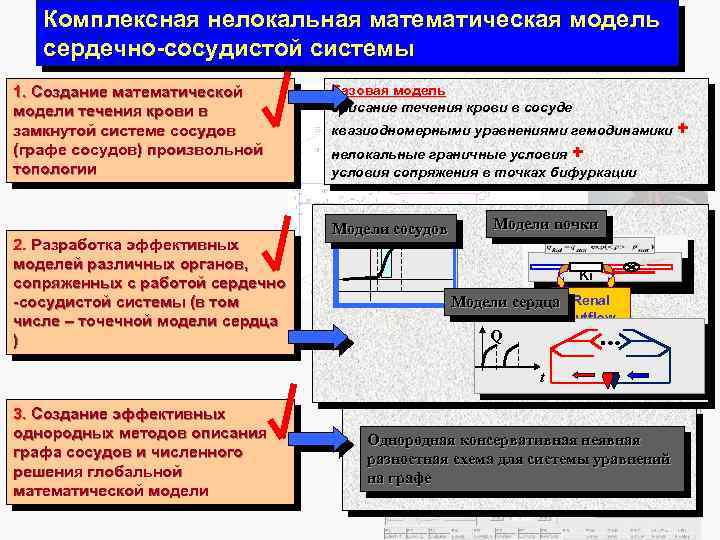
Комплексная нелокальная математическая модель сердечно-сосудистой системы 1. Создание математической модели течения крови в замкнутой системе сосудов (графе сосудов) произвольной топологии 2. Разработка эффективных моделей различных органов, сопряженных с работой сердечно -сосудистой системы (в том числе – точечной модели сердца ) Базовая модель описание течения крови в сосуде квазиодномерными уравнениями гемодинамики + нелокальные граничные условия + условия сопряжения в точках бифуркации Модели сосудов S Модели почки Ki dn Модели сердца Renal p ey outflow qkid Q t 3. Создание эффективных однородных методов описания графа сосудов и численного решения глобальной математической модели Однородная консервативная неявная разностная схема для системы уравнений на графе
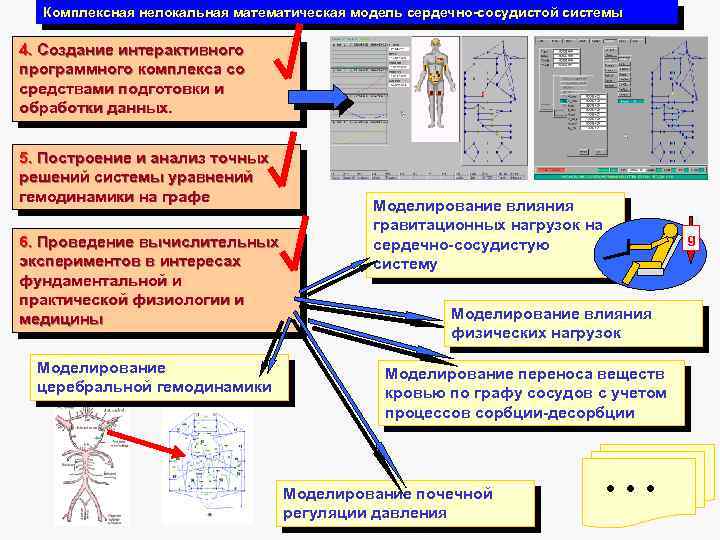
Комплексная нелокальная математическая модель сердечно-сосудистой системы 4. Создание интерактивного программного комплекса со средствами подготовки и обработки данных. 5. Построение и анализ точных решений системы уравнений гемодинамики на графе 6. Проведение вычислительных экспериментов в интересах фундаментальной и практической физиологии и медицины Моделирование церебральной гемодинамики Моделирование влияния гравитационных нагрузок на сердечно-сосудистую систему g Моделирование влияния физических нагрузок Моделирование переноса веществ кровью по графу сосудов с учетом процессов сорбции-десорбции Моделирование почечной регуляции давления . . .
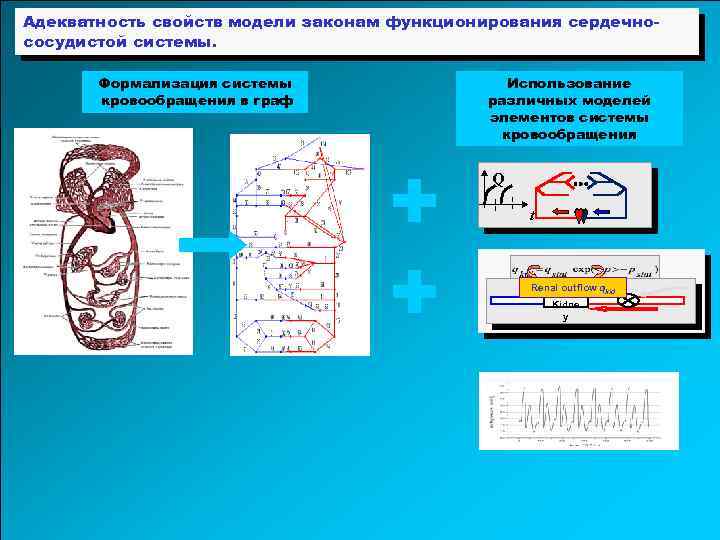
Адекватность свойств модели законам функционирования сердечнососудистой системы. Формализация системы кровообращения в граф + + Использование различных моделей элементов системы кровообращения Q t Renal outflow qkid Kidne y
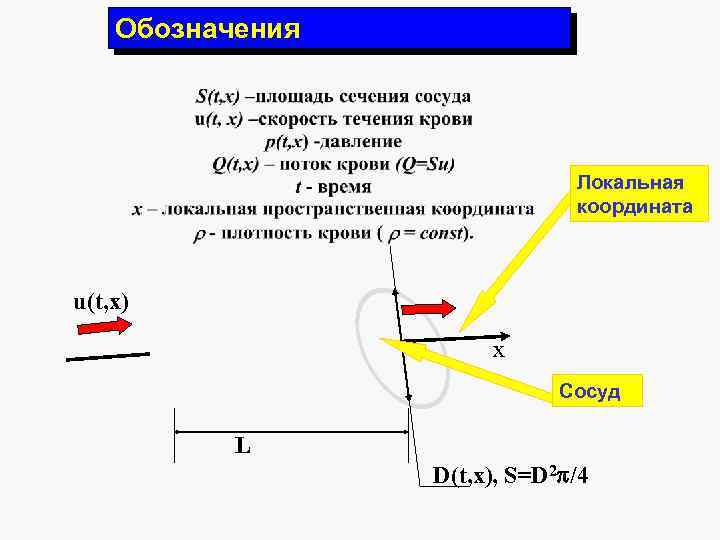
Обозначения Локальная координата u(t, x) x Сосуд L D(t, x), S=D 2 /4

Модель гемодинамики в одном сосуде Одиночный сосуд рассматриваем как трубку кругового сечения, протяженную по сравнению со своими поперечными размерами. Под эластичностью стенок понимается возможность изменения сечения сосуда под действием давления. S(x 2) S(x 1) X X 1 X 2 x- координата вдоль оси сосуда, t - время, S(x, t) - площадь сечения сосуда, u(x, t) скорость движения крови (направлена вдоль оси сосуда), p(x, t) - давление в крови, =const - плотность крови, L- длина сосуда, F(x, t) объемная плотность силы. В основу описания движения крови в сосуде положены законы сохранения массы и импульса (количества движения). Интегральный вид уравнений S=S(p) – Эмпирическая зависимость площади сечения сосуда от давления.
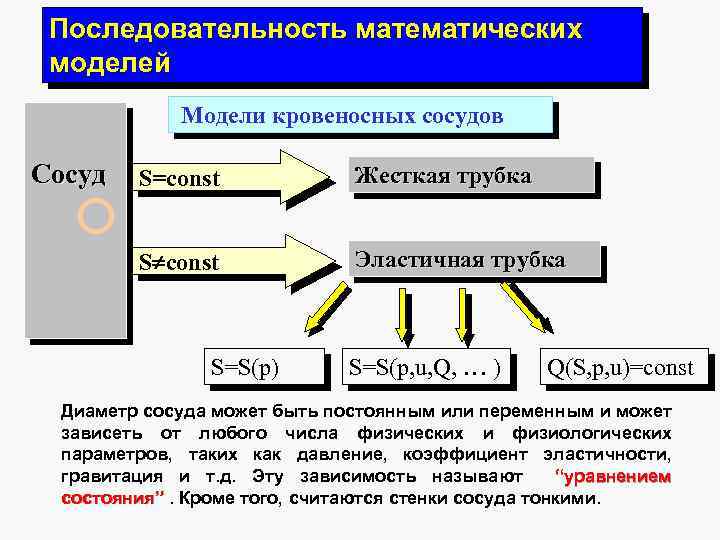
Последовательность математических моделей Модели кровеносных сосудов Сосуд S=const Жесткая трубка S const Эластичная трубка S=S(p) S=S(p, u, Q, … ) Q(S, p, u)=const Диаметр сосуда может быть постоянным или переменным и может зависеть от любого числа физических и физиологических параметров, таких как давление, коэффициент эластичности, гравитация и т. д. Эту зависимость называют “уравнением состояния”. Кроме того, считаются стенки сосуда тонкими.
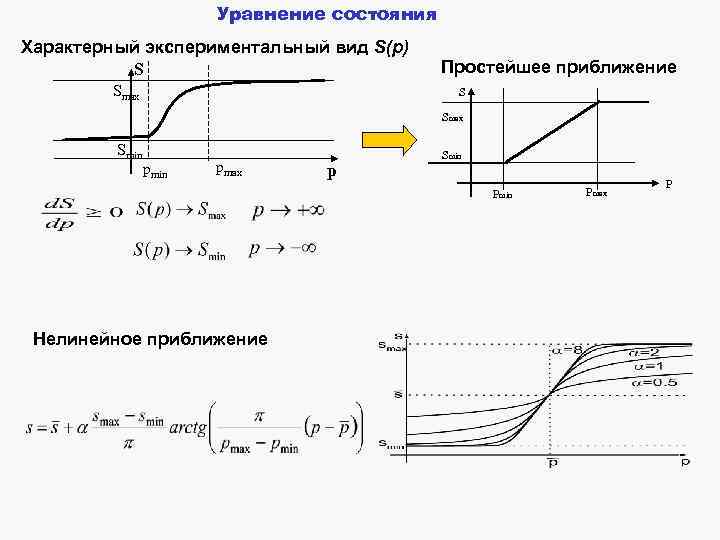
Уравнение состояния Характерный экспериментальный вид S(p) S Smax Простейшее приближение S Smax Smin pmax p Smin Pmin Нелинейное приближение Pmax P

Типичное «уравнение состояния» сосуда S В области нормальных значений давления зависимость площади поперечного сечения сосудов от давления близка к линейной. Smax Smin pmax Простейшая математическая модель “уравнения состояния” p S Smax Smin pmax p Зависимость площади поперечного сечения от давления для большинства сосудов может моделироваться этим уравнением как в нормальном состоянии, так даже и в случае некоторых патологий. Заметим, что параметры Smin , Smax, Pmin, Pmax могут быть функциями времени t и пространственной переменной x. Например, стеноз, вызванный атеросклерозом, может быть промоделирован таким образом.
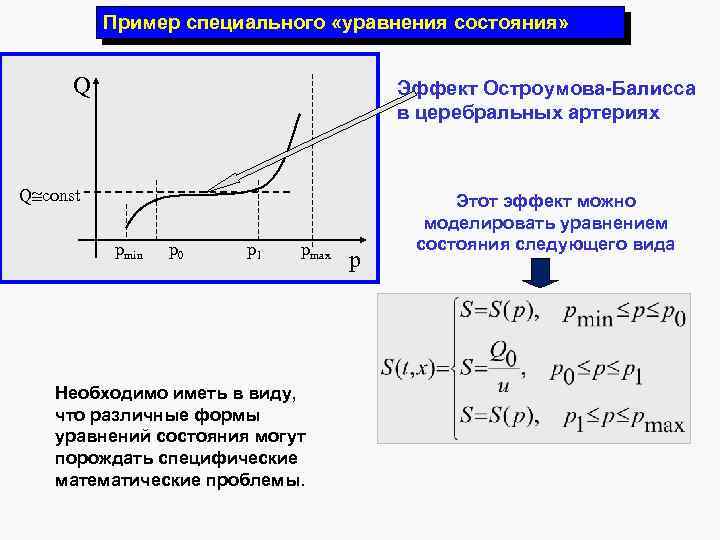
Пример специального «уравнения состояния» Q Эффект Остроумова-Балисса в церебральных артериях Q const pmin p 0 p 1 pmax Необходимо иметь в виду, что различные формы уравнений состояния могут порождать специфические математические проблемы. p Этот эффект можно моделировать уравнением состояния следующего вида
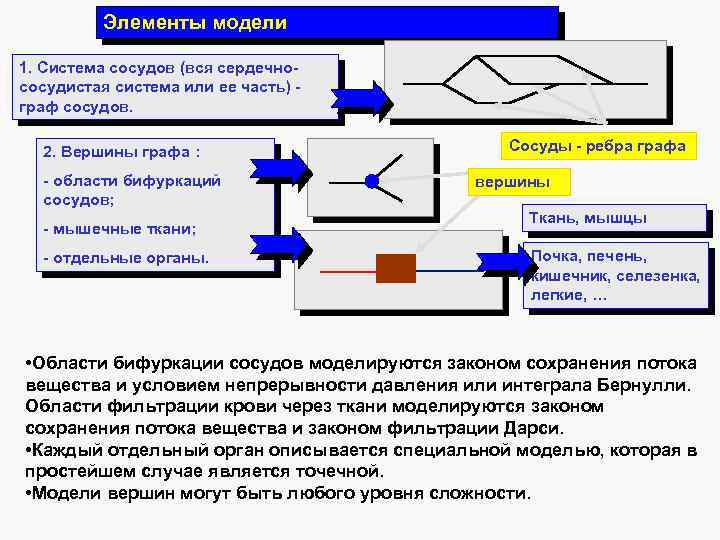
Элементы модели 1. Система сосудов (вся сердечнососудистая система или ее часть) граф сосудов. 2. Вершины графа : - области бифуркаций сосудов; - мышечные ткани; - отдельные органы. Сосуды - ребра графа вершины Ткань, мышцы Почка, печень, кишечник, селезенка, легкие, … • Области бифуркации сосудов моделируются законом сохранения потока вещества и условием непрерывности давления или интеграла Бернулли. Области фильтрации крови через ткани моделируются законом сохранения потока вещества и законом фильтрации Дарси. • Каждый отдельный орган описывается специальной моделью, которая в простейшем случае является точечной. • Модели вершин могут быть любого уровня сложности.
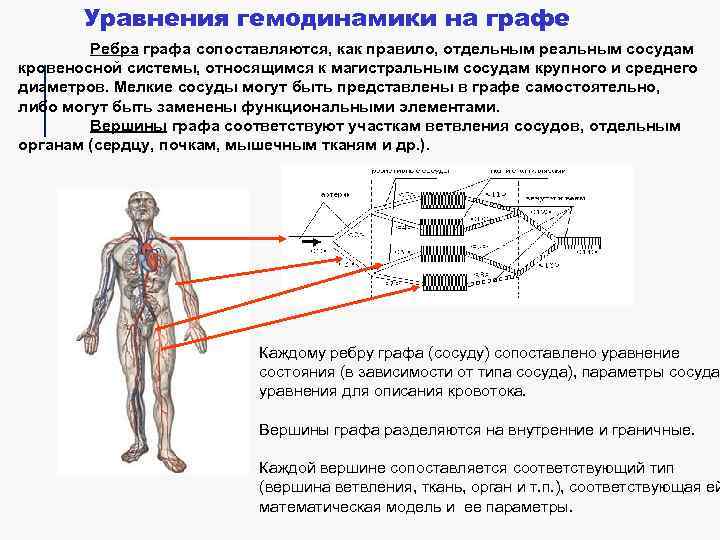
Уравнения гемодинамики на графе Ребра графа сопоставляются, как правило, отдельным реальным сосудам кровеносной системы, относящимся к магистральным сосудам крупного и среднего диаметров. Мелкие сосуды могут быть представлены в графе самостоятельно, либо могут быть заменены функциональными элементами. Вершины графа соответствуют участкам ветвления сосудов, отдельным органам (сердцу, почкам, мышечным тканям и др. ). Каждому ребру графа (сосуду) сопоставлено уравнение состояния (в зависимости от типа сосуда), параметры сосуда уравнения для описания кровотока. Вершины графа разделяются на внутренние и граничные. Каждой вершине сопоставляется соответствующий тип (вершина ветвления, ткань, орган и т. п. ), соответствующая ей математическая модель и ее параметры.
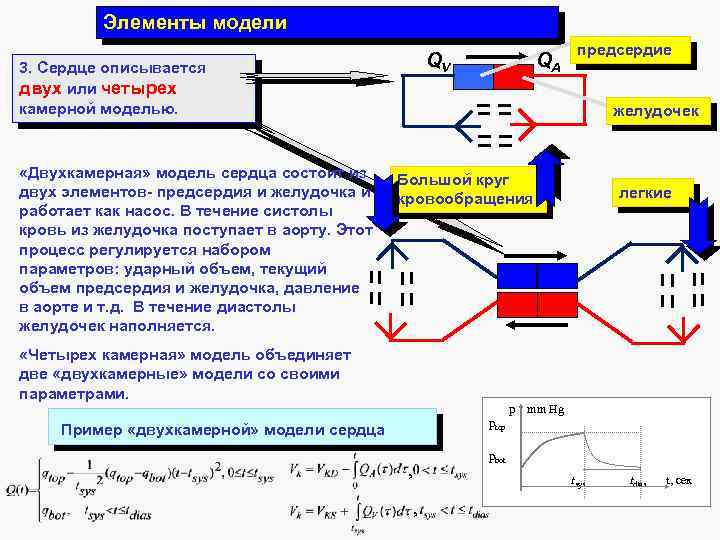
Элементы модели 3. Сердце описывается двух или четырех камерной моделью. «Двухкамерная» модель сердца состоит из двух элементов- предсердия и желудочка и работает как насос. В течение систолы кровь из желудочка поступает в аорту. Этот процесс регулируется набором параметров: ударный объем, текущий объем предсердия и желудочка, давление в аорте и т. д. В течение диастолы желудочек наполняется. QA QV предсердие желудочек Большой круг кровообращения «Четырех камерная» модель объединяет две «двухкамерные» модели со своими параметрами. p легкие mm Hg ptop Пример «двухкамерной» модели сердца pbot , tsys , tdias t, сек
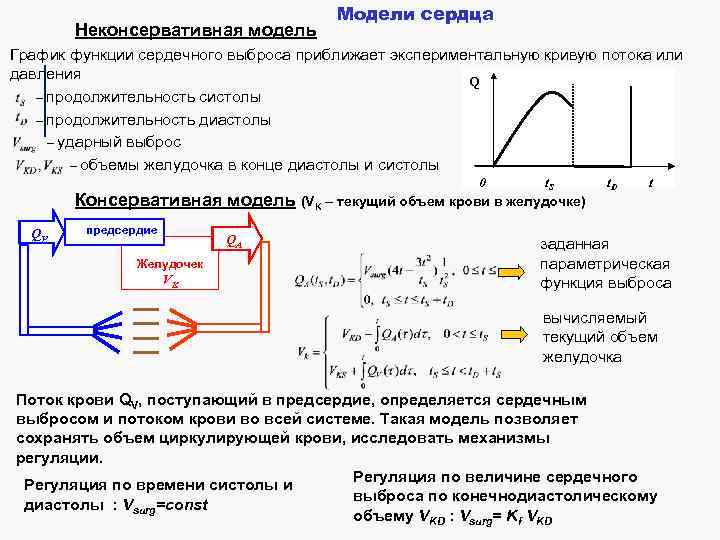
Неконсервативная модель Модели сердца График функции сердечного выброса приближает экспериментальную кривую потока или давления Q – продолжительность систолы – продолжительность диастолы – ударный выброс – объемы желудочка в конце диастолы и систолы Консервативная модель QV предсердие QA Желудочек VK 0 t. S (VK – текущий объем крови в желудочке) t. D t заданная параметрическая функция выброса вычисляемый текущий объем желудочка Поток крови QV, поступающий в предсердие, определяется сердечным выбросом и потоком крови во всей системе. Такая модель позволяет сохранять объем циркулирующей крови, исследовать механизмы регуляции. Регуляция по величине сердечного Регуляция по времени систолы и выброса по конечнодиастолическому диастолы : Vsurg=const объему VKD : Vsurg= Kf VKD
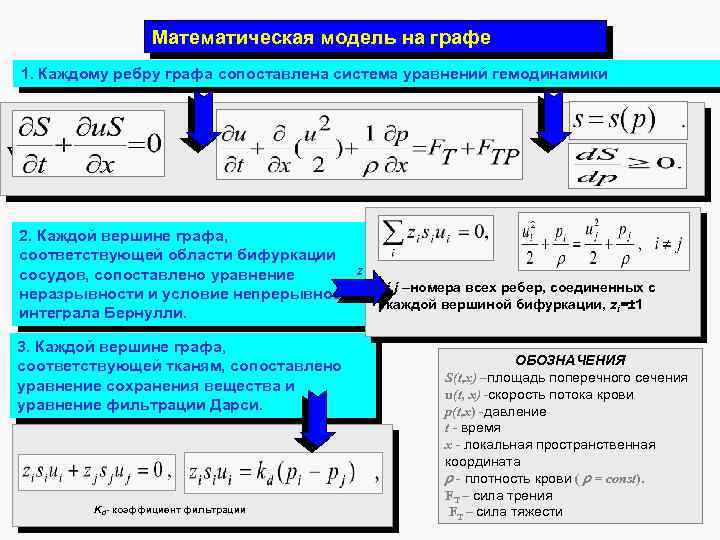
Математическая модель на графе 1. Каждому ребру графа сопоставлена система уравнений гемодинамики v 2. Каждой вершине графа, соответствующей области бифуркации сосудов, сопоставлено уравнение неразрывности и условие непрерывности интеграла Бернулли. 3. Каждой вершине графа, соответствующей тканям, сопоставлено уравнение сохранения вещества и уравнение фильтрации Дарси. Kd- коэффициент фильтрации i, j –номера всех ребер, соединенных с каждой вершиной бифуркации, zi=± 1 ОБОЗНАЧЕНИЯ S(t, x) –площадь поперечного сечения u(t, x) -скорость потока крови p(t, x) -давление t - время x - локальная пространственная координата - плотность крови ( = const). FT – сила трения FT – сила тяжести

Свойства уравнений гемодинамики ( ГД ) Система уравнений гемодинамики ( ГД ) имеет гиперболический тип при условии, что для уравнения состояния выполнено неравенство d. S/dp>0. В этом случае имеется две характеристики, два соотношения на характеристиках, скорость распространения малых возмущений. Так как давление в кровеносной системе мало отклоняется от своего среднего значения, в ряде случаев поведение системы удовлетворительно описывается линеаризованными уравнениями гемодинамики ( ЛГД ). Характеристики Скорость малых возмущений Соотношения на характеристиках s=s(p)
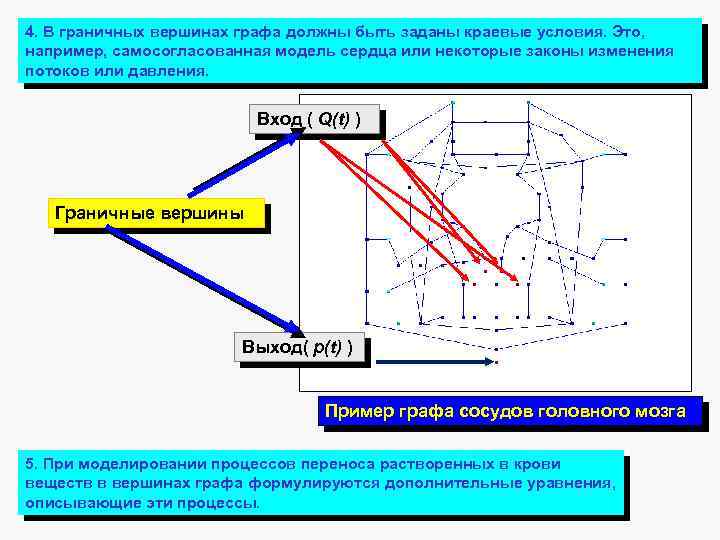
4. В граничных вершинах графа должны быть заданы краевые условия. Это, например, самосогласованная модель сердца или некоторые законы изменения потоков или давления. Вход ( Q(t) ) Граничные вершины Выход( p(t) ) Пример графа сосудов головного мозга 5. При моделировании процессов переноса растворенных в крови веществ в вершинах графа формулируются дополнительные уравнения, описывающие эти процессы.

Перенос веществ по графу сосудов Перенос вещества с массовой концентрацией C с учетом диффузии (D=constкоэффициент диффузии) по сосуду с переменным сечением описывается дифференциальным уравнением число Маха М<<1 , сечение сосудов ограничено снизу Уравнения переноса вещества для графа Сl, k – концентрация l-ого вещества в k –ом сосуде, f – источник , - химические реакции. В вершинах ветвления - закон Киргхофа с учетом диффузии и равенство соответствующих концентраций. Уравнения для концентраций в сердце Рассматривается случай полного перемешивания веществ Cl в желудочке. Позволяют рассматривать замкнутую систему кровообращения с сохранением количества веществ во всей системе. Здесь t – время начала диастолы, а t изменяется от нуля до величины равной продолжительности диастолы. Индекс a обозначает аорту. Аналогичное выражение выписывается для концентраций во время систолы.
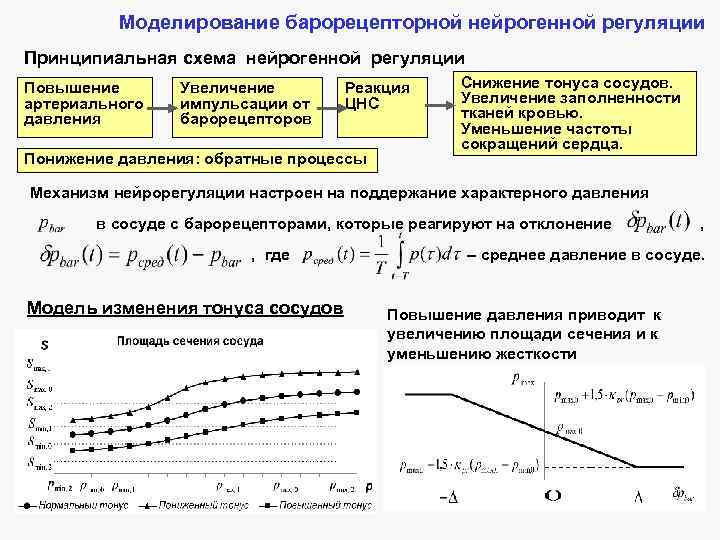
Моделирование барорецепторной нейрогенной регуляции Принципиальная схема нейрогенной регуляции Повышение артериального давления Увеличение импульсации от барорецепторов Реакция ЦНС Понижение давления: обратные процессы Снижение тонуса сосудов. Увеличение заполненности тканей кровью. Уменьшение частоты сокращений сердца. Механизм нейрорегуляции настроен на поддержание характерного давления в сосуде с барорецепторами, которые реагируют на отклонение , где Модель изменения тонуса сосудов , – среднее давление в сосуде. Повышение давления приводит к увеличению площади сечения и к уменьшению жесткости

Моделирование барорецепторной нейрогенной регуляции Модель изменения наполненности капилляров (тканей) Повышение (уменьшение) давления приводит к увеличению (уменьшению) количества капилляров в тканях, заполненных кровью. В рамках точечных моделей это можно интерпретировать как увеличение (уменьшение) коэффициента фильтрации в законе Дарси Модель изменения частоты сокращения сердца Повышение (уменьшение) давления приводит к увеличению (уменьшению) продолжительности сердечного цикла tprd.
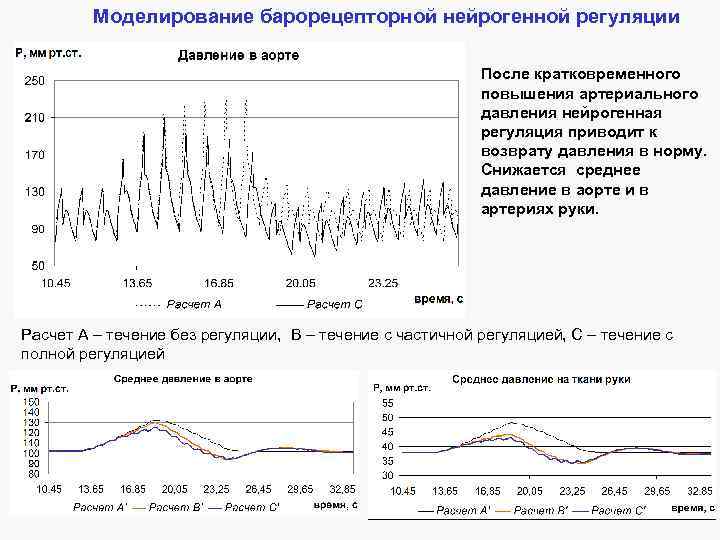
Моделирование барорецепторной нейрогенной регуляции После кратковременного повышения артериального давления нейрогенная регуляция приводит к возврату давления в норму. Снижается среднее давление в аорте и в артериях руки. Расчет А – течение без регуляции, B – течение с частичной регуляцией, С – течение с полной регуляцией
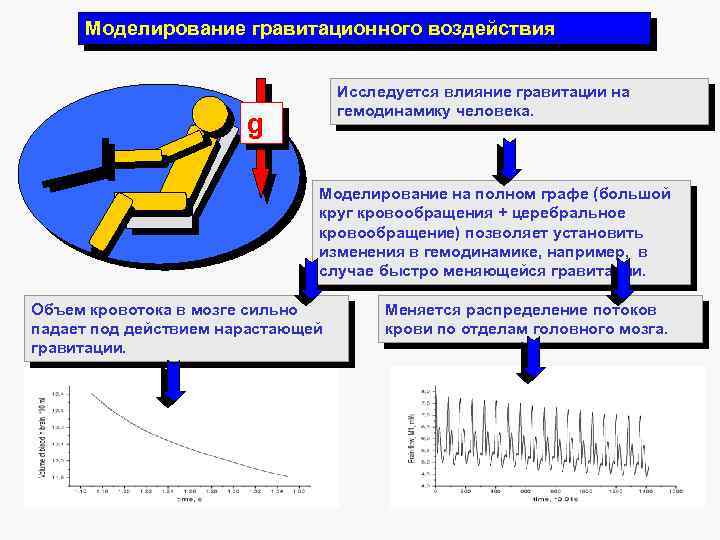
Моделирование гравитационного воздействия Исследуется влияние гравитации на гемодинамику человека. g Моделирование на полном графе (большой круг кровообращения + церебральное кровообращение) позволяет установить изменения в гемодинамике, например, в случае быстро меняющейся гравитации. Объем кровотока в мозге сильно падает под действием нарастающей гравитации. Меняется распределение потоков крови по отделам головного мозга.
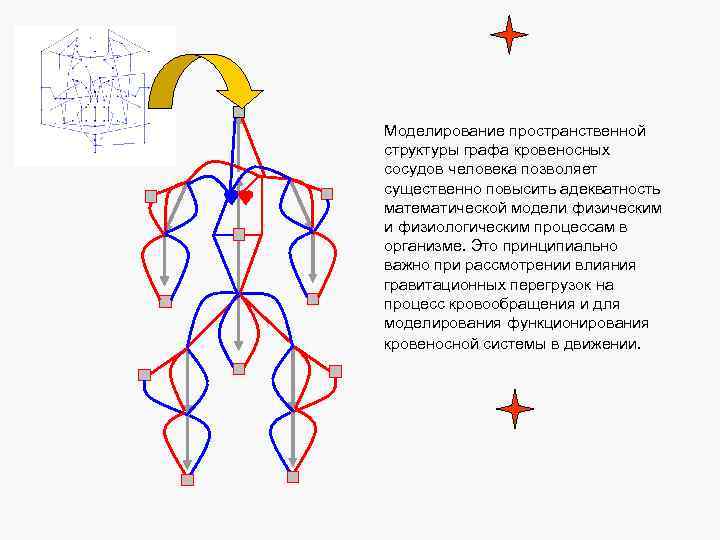
Моделирование пространственной структуры графа кровеносных сосудов человека позволяет существенно повысить адекватность математической модели физическим и физиологическим процессам в организме. Это принципиально важно при рассмотрении влияния гравитационных перегрузок на процесс кровообращения и для моделирования функционирования кровеносной системы в движении.
Лекция 4_5_Классификация и моделирование биотехнических систем.pptx