Классическая химия и квантовая механика КЛАССИЧЕСКАЯ ХИМИЯ

Классическая химия и квантовая механика

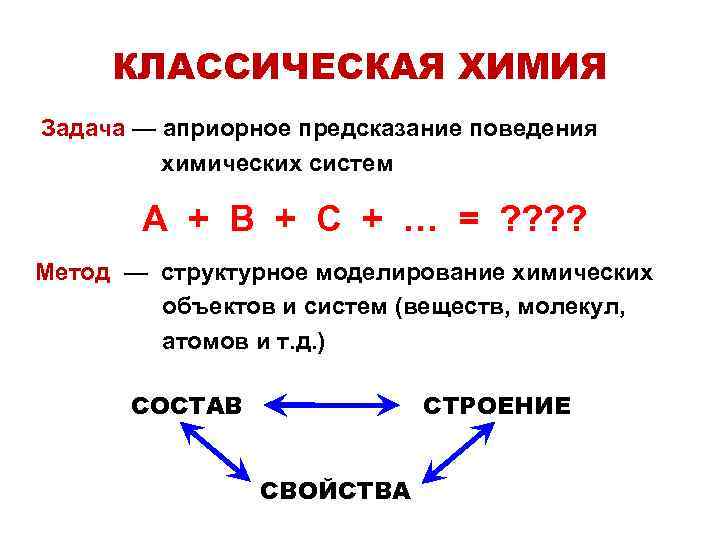КЛАССИЧЕСКАЯ ХИМИЯ Задача — априорное предсказание поведения химических систем А + В + С + … = ? ? Метод — структурное моделирование химических объектов и систем (веществ, молекул, атомов и т. д. ) СОСТАВ СТРОЕНИЕ СВОЙСТВА

Каковы химические свойства вещества Х? 1) установление химического СОСТАВА вещества 2) установление химического СТРОЕНИЯ вещества 3) предсказание химических СВОЙСТВ вещества Установление ХИМИЧЕСКОГО СОСТАВА а) классический элементный анализ б) физические методы элементного анализа (ААС, РФЭС, ЯМР и др. ) Теория физических методов — квантовая механика

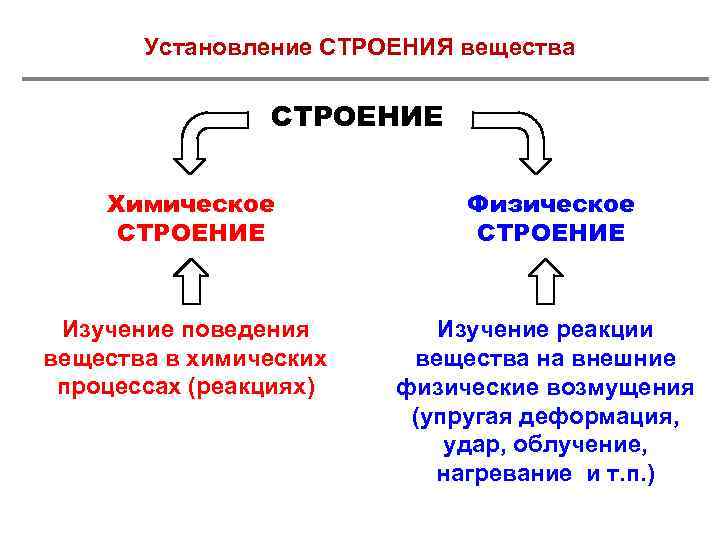Установление СТРОЕНИЯ вещества СТРОЕНИЕ Химическое СТРОЕНИЕ Физическое СТРОЕНИЕ Изучение поведения вещества в химических процессах (реакциях) Изучение реакции вещества на внешние физические возмущения (упругая деформация, удар, облучение, нагревание и т. п. )

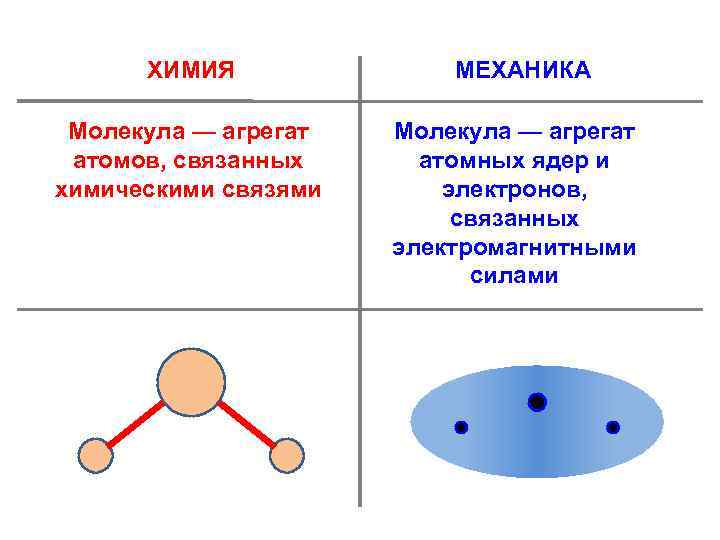ХИМИЯ Молекула — агрегат атомов, связанных химическими связями МЕХАНИКА Молекула — агрегат атомных ядер и электронов, связанных электромагнитными силами

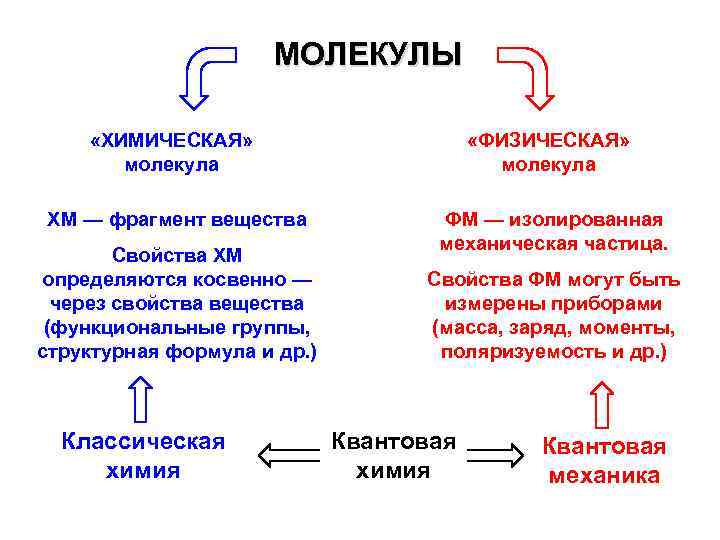МОЛЕКУЛЫ «ХИМИЧЕСКАЯ» молекула «ФИЗИЧЕСКАЯ» молекула ХМ — фрагмент вещества ФМ — изолированная механическая частица. Свойства ХМ определяются косвенно — через свойства вещества (функциональные группы, структурная формула и др. ) Классическая химия Свойства ФМ могут быть измерены приборами (масса, заряд, моменты, поляризуемость и др. ) Квантовая химия Квантовая механика

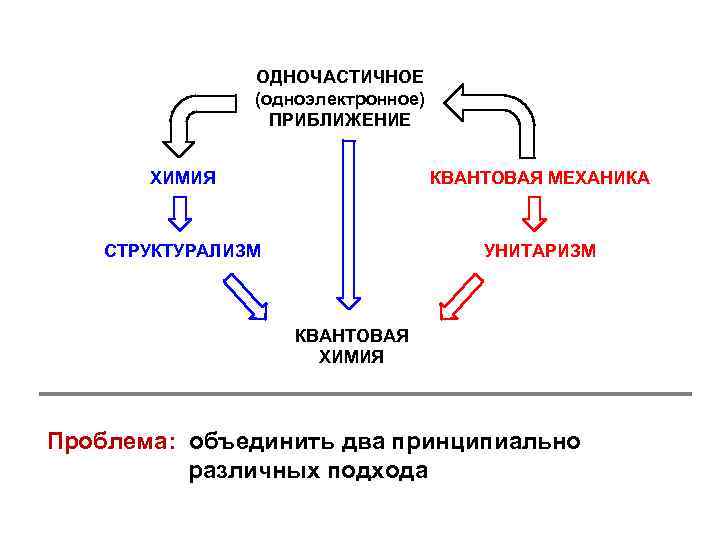ОДНОЧАСТИЧНОЕ (одноэлектронное) ПРИБЛИЖЕНИЕ ХИМИЯ КВАНТОВАЯ МЕХАНИКА СТРУКТУРАЛИЗМ УНИТАРИЗМ КВАНТОВАЯ ХИМИЯ Проблема: объединить два принципиально различных подхода

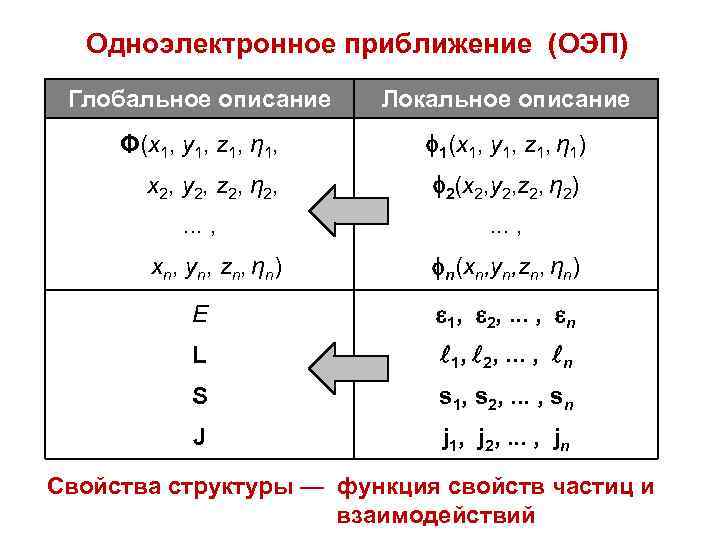Одноэлектронное приближение (ОЭП) Глобальное описание Локальное описание Φ(x 1, y 1, z 1, η 1, 1(x 1, y 1, z 1, η 1) x 2, y 2, z 2, η 2, 2(x 2, y 2, z 2, η 2) . . . , xn, yn, zn, ηn) . . . , n(xn, yn, zn, ηn) E 1, 2, . . . , n L 1, 2, . . . , n S s 1, s 2, . . . , sn J j 1, j 2, . . . , jn Свойства структуры — функция свойств частиц и взаимодействий

07. 10. 2015

Одноэлектронное приближение Каждому электрону приписывается: • индивидуальная функция — «молекулярная орбиталь» (МО) i (xi, yi, zi, ηi) • набор одноэлектронных наблюдаемых i Спин-орбиталь (МСО) ji i si Орбиталь (МО) i (xi, yi, zi, ηi) = i (xi, yi, zi) i (ηi) Пространственный множитель Спиновой множитель

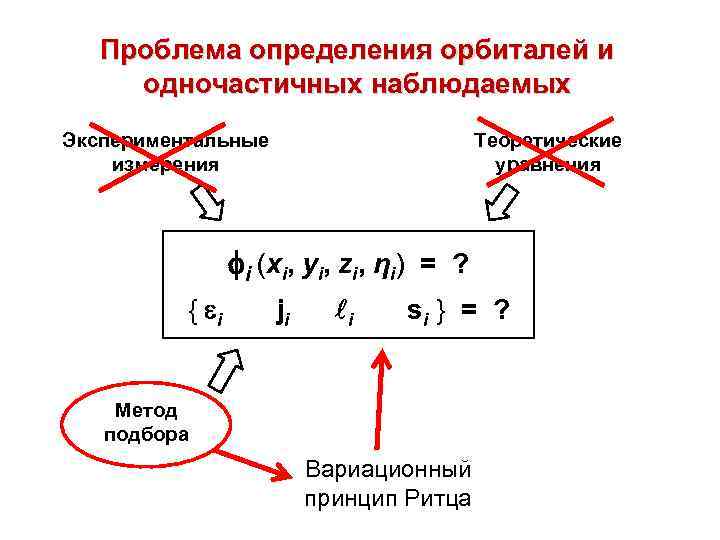Проблема определения орбиталей и одночастичных наблюдаемых Экспериментальные измерения Теоретические уравнения i (xi, yi, zi, ηi) = ? { i ji i si } = ? Метод подбора Вариационный принцип Ритца

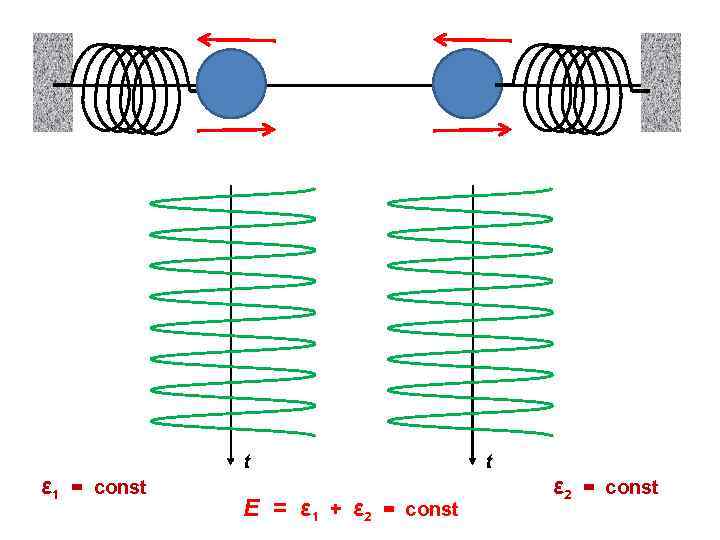ε 1 = const t E = ε 1 + ε 2 = const t ε 2 = const

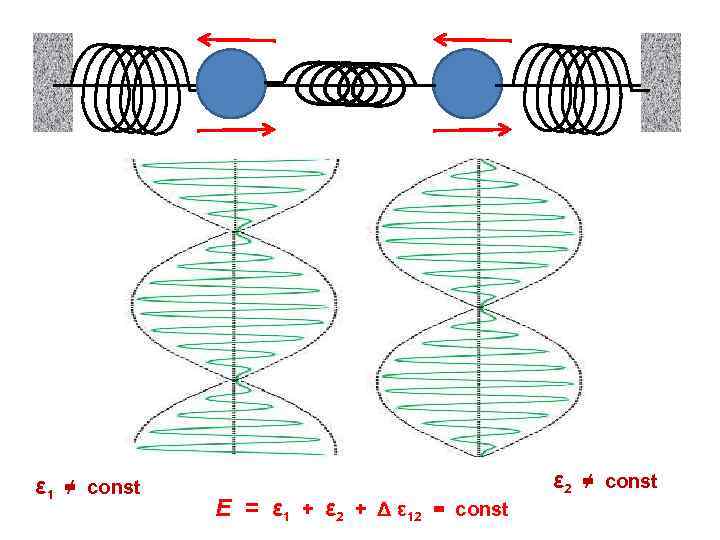ε 1 ≠ const E = ε 1 + ε 2 + Δ ε 12 = const ε 2 ≠ const

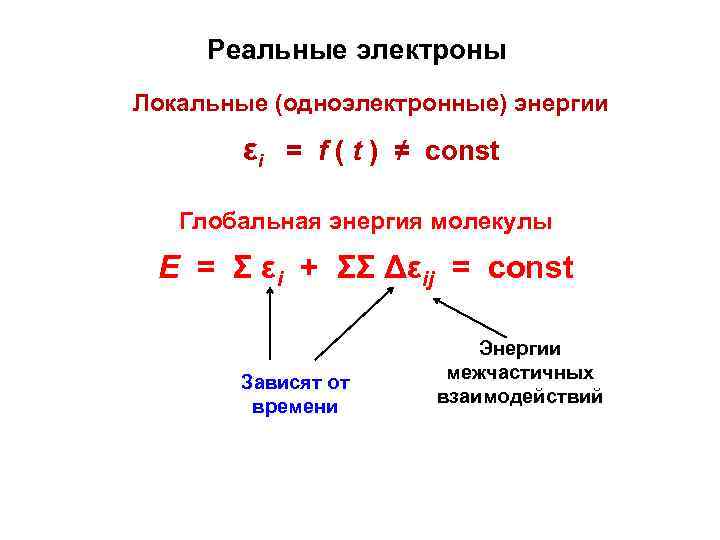Реальные электроны Локальные (одноэлектронные) энергии εi = f ( t ) ≠ const Глобальная энергия молекулы Е = Σ εi + ΣΣ Δεij = const Зависят от времени Энергии межчастичных взаимодействий

Квази-электроны (орбитальная модель) Е = Σ ( εi )* + ΔΕ = const ( εi )* = const Орбитальная энергия (εi)* — это реальная энергия электрона, усредненная за большой промежуток времени: ( εi )* = εi t Полная межчастичная энергия также усредняется по времени и становится постоянной величиной: ΔЕ = ΣΣ Δεij t = const

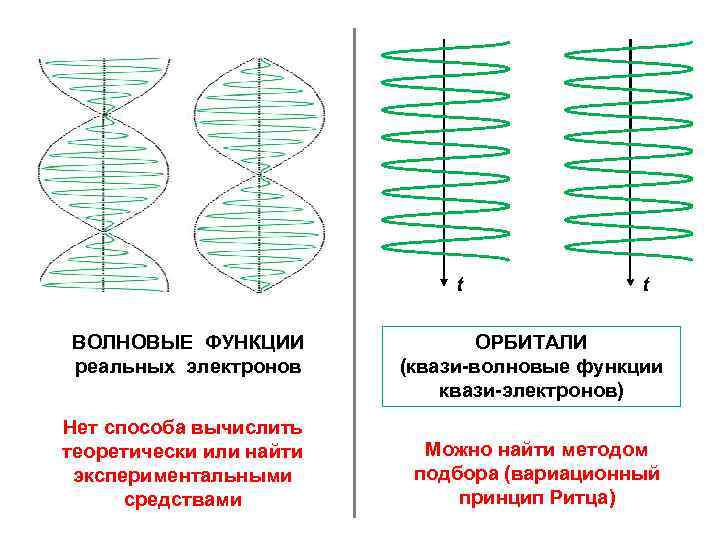t ВОЛНОВЫЕ ФУНКЦИИ реальных электронов Нет способа вычислить теоретически или найти экспериментальными средствами t ОРБИТАЛИ (квази-волновые функции квази-электронов) Можно найти методом подбора (вариационный принцип Ритца)

Вариационный принцип Ритца Электроны сами выбирают наиболее простые и экономные способы движения, признаком которых является минимум полной энергии молекулы: E = min Необходимо последовательно решить две задачи: 1) выразить полную энергию как функцию набора орбиталей Е = Е ( 1 , …, i , …, n) 2) найти минимум этой функции Е=0

Глобальная волновая функция молекулы φ1(1) φ2(1) φn(1) φ1(2) φ2(2) φn(2) 1 Ф = ——. . n! φ1(n) φ2(n) φn(n) Определитель Слэтера Каков явный вид МО? Вариант МО ЛКАО 1 = С 11 1 + С 12 2 + … + С 1 n n 2 = С 21 1 + С 22 2 + … + С 2 n n ……………………. n = Сn 1 1 + Сn 2 2 + … + Сnn n

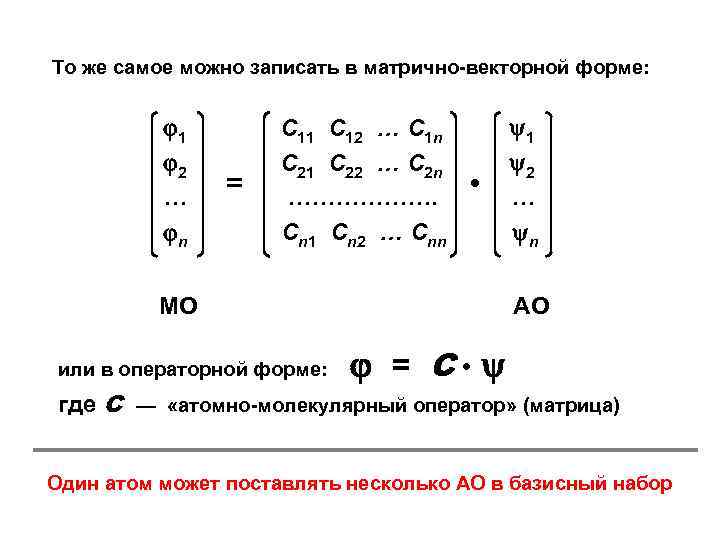То же самое можно записать в матрично-векторной форме: 1 2 … n = С 11 С 12 … С 1 n С 21 С 22 … С 2 n ………………. Сn 1 Сn 2 … Сnn • МО или в операторной форме: 1 2 … n АО = С • где С — «атомно-молекулярный оператор» (матрица) Один атом может поставлять несколько АО в базисный набор

Уравнения Хартри-Фока-Рутана F – S . . F n – S n С . . • . . . Fn – Sn . . Fnn – Snn = 0 Сn F — матричные элементы оператора Фока, характеризующие либо энергию электрона в изолированном атоме с номером (при = ), либо изменение энергии электрона при его обобществлении двумя атомами с номерами и (при ≠ ), S — интегралы перекрывания для базисных АО с номерами и , — энергия МО с коэффициентами {С С … Сn }.

F – S . . F n – S n . . . . = 0 . Fn – Sn . . Fnn – Snn Характеристическое уравнение Аn n + Аn– 1 + … + А 1 + Аo = 0 где Ai = f (F , S ) i ХФР { 1, 2, … , n } { Сα, Сβ, …, Сn }i

Итерационная процедура { Cij }о { F , S }о ХФР { i }o { Cij }1 { F , S }1 ХФР { i }1 { Cij }2 { F , S }2 ХФР { i }2 . . . . { Cij }m { F , S }m ХФР { i }m { Cij }* { F , S }* ХФР { i }* { Cij }о — пробный набор коэффициентов МО { Cij }* — самосогласованный набор коэффициентов МО { i }* — самосогласованные орбитальные энергии

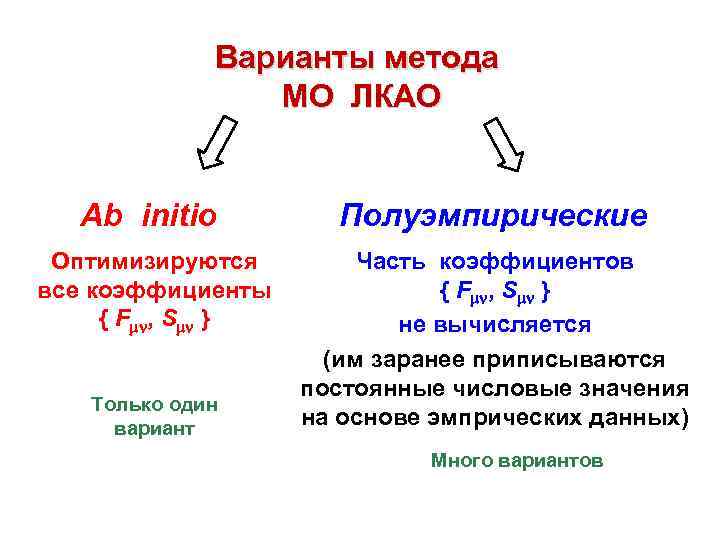Варианты метода МО ЛКАО Ab initio Полуэмпирические Оптимизируются все коэффициенты { F , S } Часть коэффициентов { F , S } не вычисляется (им заранее приписываются постоянные числовые значения на основе эмпрических данных) Только один вариант Много вариантов

Выводы 1. Согласование классической химии и квантовой механики достигается за счет использования специальной модели — одноэлектронного приближения (ОЭП), • смысл ОЭП сводится к усреднению быстрого реального движения электрона и замене его статичным «электронным облаком» . 2. Основная задача ОЭП — найти для каждого электрона специфическую функцию — молекулярную орбиталь, которая характеризует все особенности движения этого электрона (электронного облака) в молекуле.

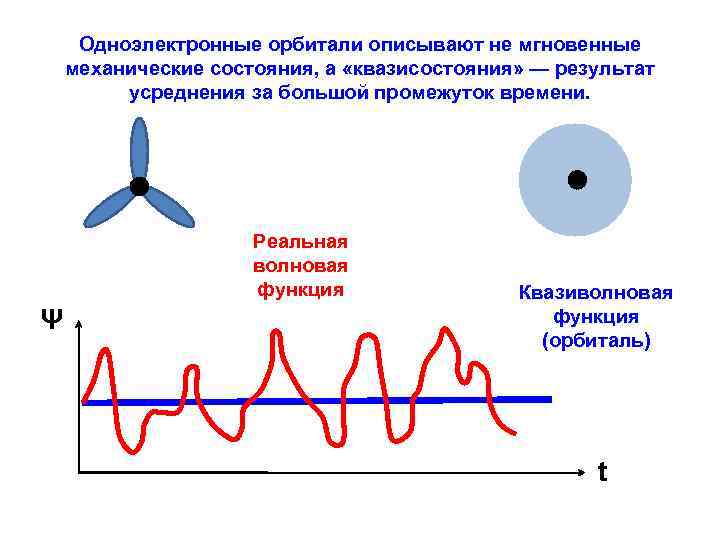Одноэлектронные орбитали описывают не мгновенные механические состояния, а «квазисостояния» — результат усреднения за большой промежуток времени. Реальная волновая функция Ψ Квазиволновая функция (орбиталь) t

Вопрос: почему неправильное одноэлектронное приближение позволяет получать правильные решения химических задач? Ответ: потому что химия занимается только «медленными» (по сравнению с движением самих электронов) процессами — перемещениями атомов и молекул.