КЛАССИЧЕСКАЯ МЕХАНИКА Макромир 1643 — 1727 1564 —

КЛАССИЧЕСКАЯ МЕХАНИКА Макромир 1643 - 1727 1564 - 1642 Основная задача механики: если известно механическое состояние системы (совокупность координат и скоростей) в момент времени , определить механическое состояние системы в момент времени.

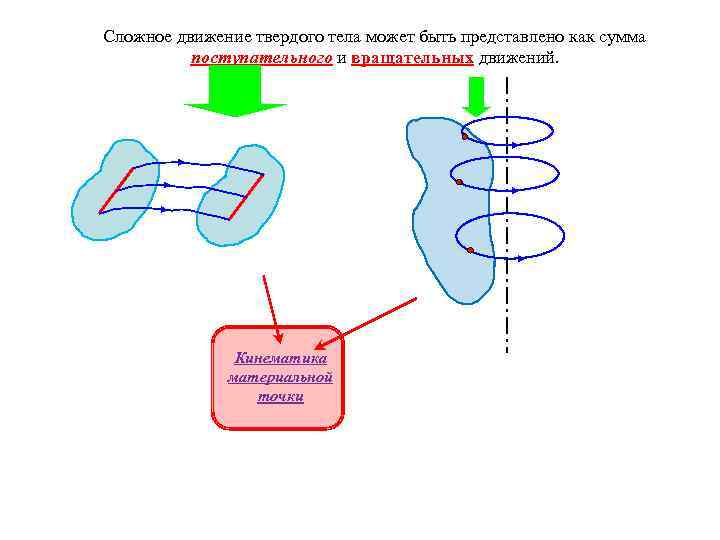Сложное движение твердого тела может быть представлено как сумма поступательного и вращательных движений. Кинематика материальной точки

• Поступательное движение тела • – движение тела, при котором прямая, соединяющая две любые точки тела, остается параллельной самой себе при движении этого тела. • Следствие – все точки тела движутся по одинаковым траекториям. Вращательное движение тела вокруг оси – движение тела, при котором все точки тела описывают окружности в плоскостях, перпендикулярных к оси вращения, и с центрами, лежащими на этой оси. Материальная точкатело размерами и формой которого можно пренебречь в условиях данной задачи.

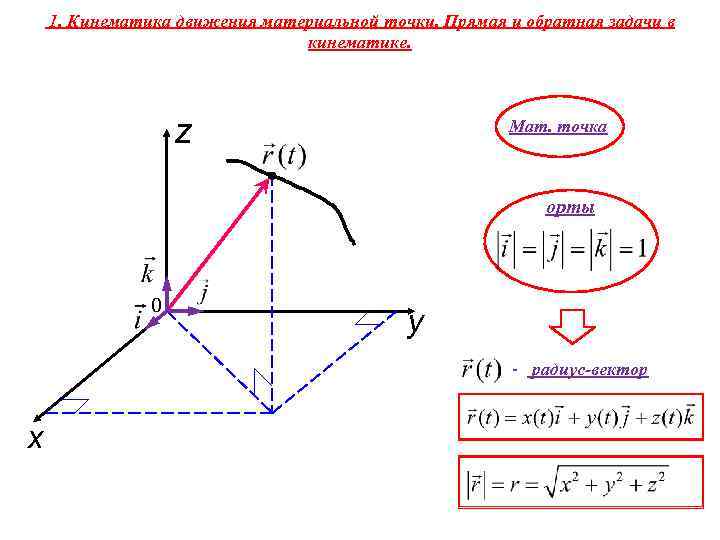1. Кинематика движения материальной точки. Прямая и обратная задачи в кинематике. z Мат. точка орты 0 y - радиус-вектор x

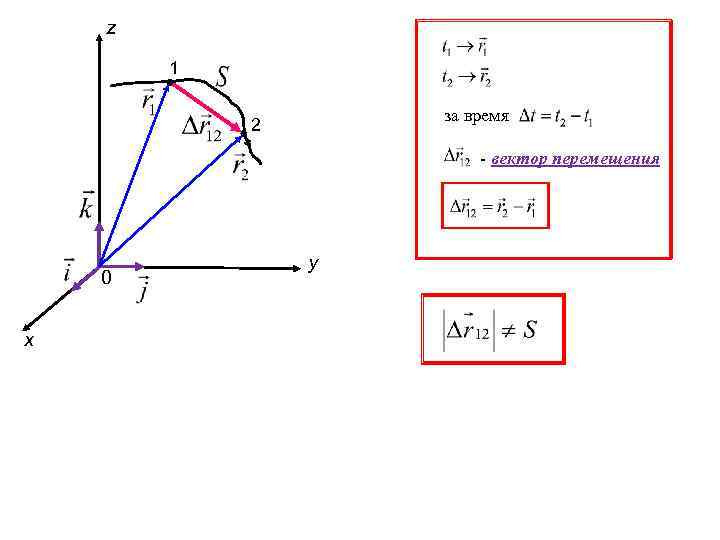z 1 за время 2 - вектор перемещения 0 x y

- элементарное перемещение за время -элементарная длина траектории (путь) - за время z 1 2 0 x y

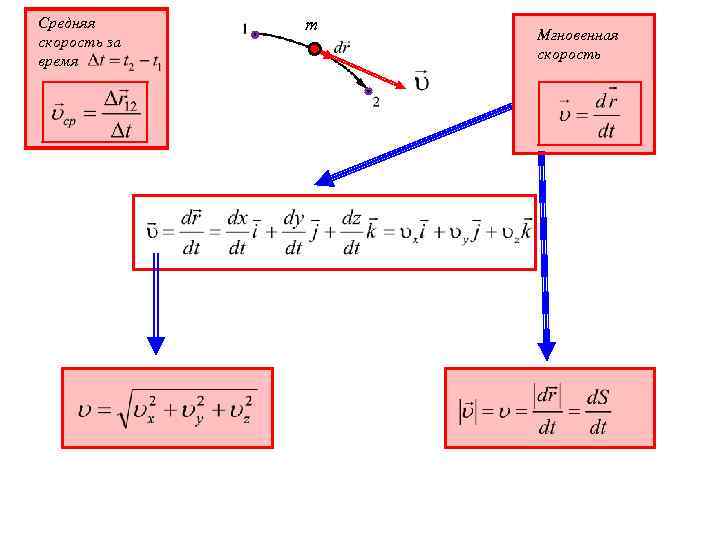Средняя скорость за время m Мгновенная скорость

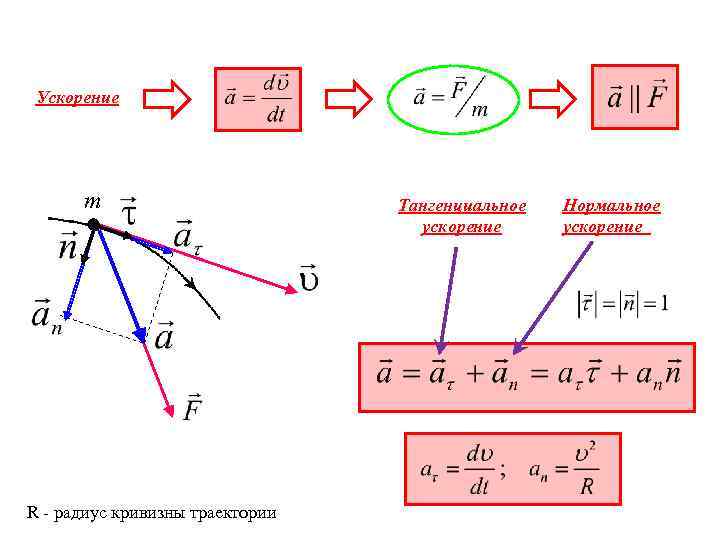Ускорение m R - радиус кривизны траектории Тангенциальное ускорение Нормальное ускорение

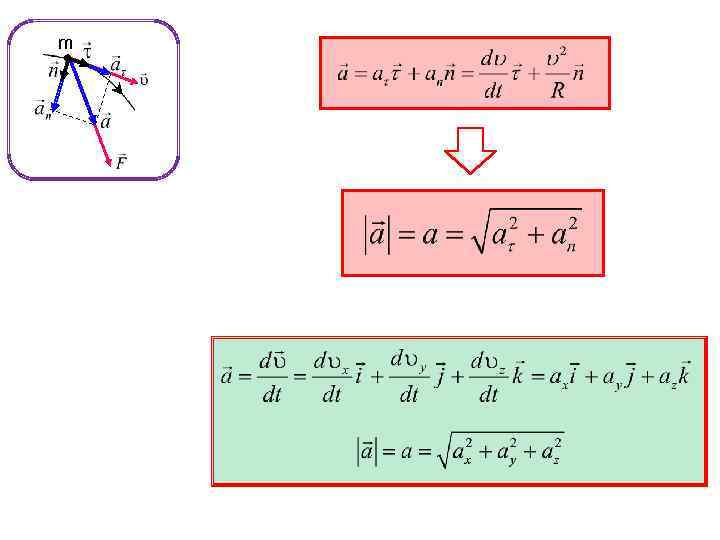m

Тангенциальное ускорение характеризует быстроту изменения модуля скорости (скорость по величине), Нормальное ускорение характеризует быстроту изменения направления вектора скорости. «Прямая и обратная задачи кинематики материальной точки» На упражнении.

Зная , можно определить все характеристики движения материальной точки в заданный момент времени.

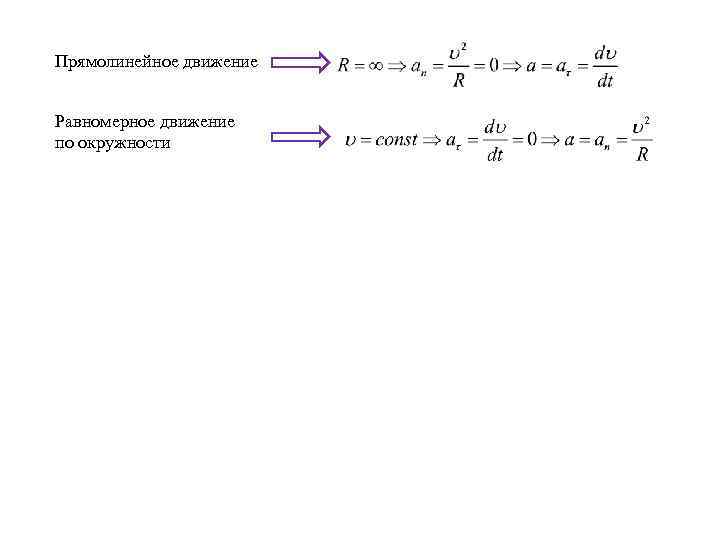Прямолинейное движение Равномерное движение по окружности