Парная регрессия и корреляция.ppt
- Количество слайдов: 59

КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ (КЛММР)

Любая экономическая политика заключается в регулировании экономических переменных, и она должна базироваться на знании того, как эти переменные связаны между собой.

В подавляющем большинстве случаев между экономическими явлениями нет строгих (функциональных) зависимостей, когда одному значению переменной соответствует единственное значение другой. В экономике рассматриваются статистические (стохастические, вероятностные) зависимости.

Можно рассмотреть два варианта взаимосвязей между двумя переменными X и Y: 1. Обе переменные считаются равноценными и не подразделяются на первичную и вторичную (независимую и зависимую) переменные. Такие связи исследуют с помощью корреляционного анализа.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной cвязи:

2. Выделяют независимую (объясняющую) переменную X и зависимую (объясняемую) переменную Y, т. е. изменение первой служит причиной для изменения другой.

При этом каждому конкретному значению объясняющей переменной может соответствовать множество значений, то есть некоторое вероятностное распределение объясняемой переменной. Поэтому анализируют, как объясняющая переменная влияет на зависимую переменную «в среднем» .

Модель парной линейной регрессии В общем виде линейную регрессионную модель можно представить в виде Y= 0+ 1 X+ , где 0, 1 – теоретические параметры (теоретические коэффициенты) регрессии; - случайное отклонение.

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно.

Таким образом, задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным (xi, yi ), i = 1, . . , n для переменных Х и Y:

1. получить наилучшие оценки неизвестных параметров 0, 1 ; 2. проверить статистические гипотезы о параметрах модели; 3. проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии ----- , где - оценка условного математического ожидания Y, b 0, b 1 – оценки неизвестных параметров 0, 1, называемые эмпирическими коэффициентами регрессии.

Следовательно, в конкретном случае yi=b 0+b 1 xi+ei, где отклонение ei – оценка теоретического случайного отклонения i. В силу несовпадения статистической базы для генеральной совокупности и выборки оценки b 0, b 1 практически всегда отличаются от истинных значений коэффициентов 0, 1.

Задача состоит в том, чтобы по конкретной выборке найти оценки параметров так, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых.

Пусть у нас есть набор значений двух переменных xi, yi, i = 1, . . , n; можно отобразить пары (xi, yi) точками на плоскости Х-Y.
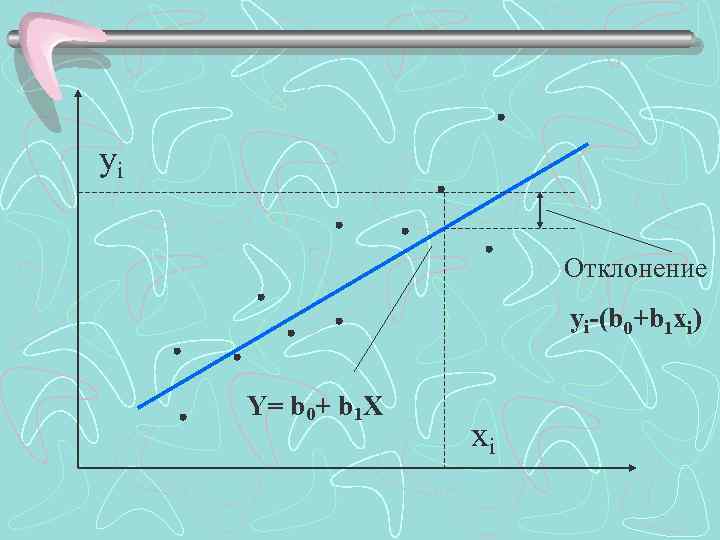
yi Отклонение yi-(b 0+b 1 xi) Y= b 0+ b 1 X xi

В качестве меры отклонения функции Y(X) от набора наблюдений можно взять: üсумму квадратов отклонений üсумму модулей отклонений

В статистическом анализе широко применяется минимизация квадратов отклонений (метод наименьших квадратов МНК). Это объясняется легкостью вычислительной процедуры и хорошими статистическими свойствами оценок.

Метод наименьших квадратов (МНК) Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений (xi, yi ), i = 1, . . . , n, линейной функцией Y = b 0 + b 1 Х в смысле минимизации функционала

Запишем необходимые условия экстремума
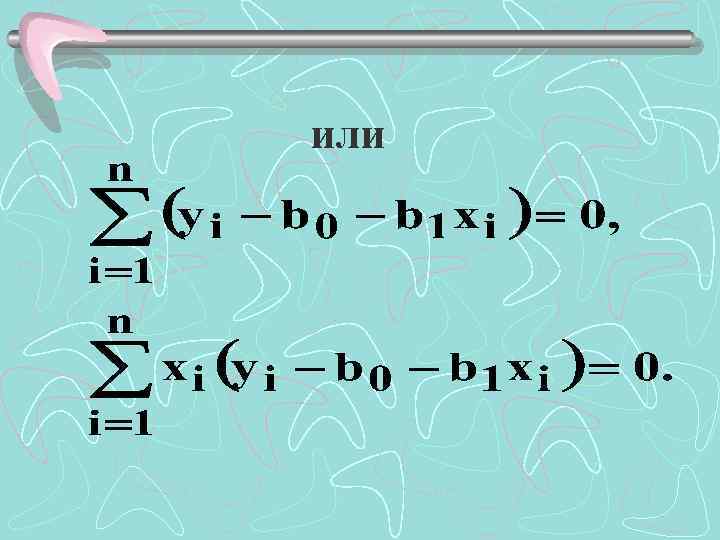
или

Раскроем скобки и получим систему уравнений

Решения системы можно легко найти

Выводы: 1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать. 2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.

3. Из последнего уравнения системы следует , т. е. эмпирическая прямая регрессии обязательно проходит через точку 4. Сумма отклонений , а также среднее значение равны нулю.

5. Случайные отклонения ei не коррелированы с наблюдаемыми значениями yi зависимой переменной Y и с наблюдаемыми значениями xi независимой переменной X: Sye=0 и Sxe=0.

Экскурс в статистику Выборочное среднее : Выборочная ковариация является мерой взаимосвязи между двумя переменными и задается формулой:

Предпосылки метода наименьших квадратов Переменная Y является СВ, напрямую связанной со случайными отклонениями i. Это означает, что свойства оценок коэффициентов регрессии, а следовательно, и качество построенной регрессии существенно зависят от свойств случайной составляющей.

Условия Гаусса-Маркова 1. Математическое ожидание случайного отклонения равно нулю: M( i ) = 0 для всех наблюдений. Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную.

В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения.

2. Дисперсия случайных отклонений i постоянна: D( i )=D( j )= 2 для любых наблюдений i и j. Это значит, что в каждом конкретном наблюдении не должно быть некой априорной причины, вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью. Данную предпосылку можно переписать в форме: M( i 2)= 2.

3. Случайные отклонения i и j являются независимыми друг от друга для i j. Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. То есть величина и знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Выполнимость данной предпосылки влечет следующее соотношение: Если данное условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнимости первой предпосылки это соотношение может быть переписано в виде: M( i j)=0 (i j).

4. Случайное отклонение должно быть независимо от объясняющих переменных. 5. Модель является линейной относительно параметров.

Теорема Гаусса-Маркова Если предпосылки 1 -5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами: 1. Оценки являются несмещенными, т. е. М(b 0)= 0, М(b 1)= 1. 2/6/2018 36

2. Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю. Другими словами, при увеличении объема выборки надежность оценок увеличивается (b 0 наверняка близко к 0, b 1 – близко к 1).

3. Оценки эффективны, т. е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров. В англоязычной литературе такие оценки называют BLUE (Best Linear Unbiased Estimators) – наилучшие линейные несмещенные оценки.

Если выполнены предпосылки 1 -5, то говорят о классической линейной регрессионной модели. Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения:

ü объясняющие переменные не являются СВ; üслучайные отклонения имеют нормальное распределение; üчисло наблюдений существенно больше числа объясняющих переменных; üотсутствуют ошибки спецификации.

Если предпосылки 2 и 3 нарушены, т. е. дисперсия отклонений непостоянна и (или) значения i, j связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.

Анализ точности определения оценок коэффициентов регрессии В силу случайного отбора элементов в выборку случайными являются также оценки b 1 и b 0 коэффициентов 1 и 0 теоретического уравнения регрессии.

Надежность получаемых оценок 2 тесно связана с дисперсией случайных отклонений i. Формулы связи дисперсий коэффициентов D(b 0) и D(b 1) с дисперсией случайных 2 : отклонений
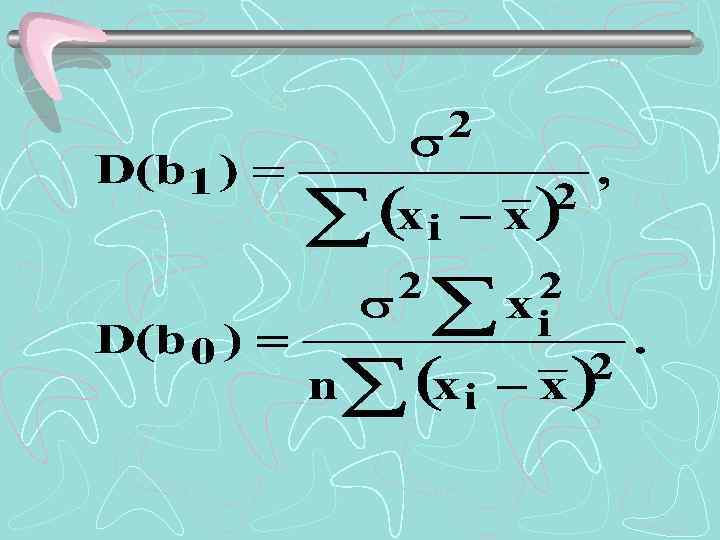

Выводы: ü Дисперсии b 0 и b 1 прямо пропорциональны дисперсии случайного отклонения. Следовательно, чем больше фактор случайности, тем менее точными будут оценки.

ü Чем больше число n наблюдений, тем меньше дисперсии оценок. Это вполне логично, так как чем большим числом данных мы располагаем, тем вероятнее получение более точных оценок.

ü Чем больше дисперсия (разброс значений ) объясняющей переменной, тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменений объясняющей переменной, тем точнее будут оценки (тем меньше доля случайности в их определении).

Дисперсия случайных отклонений заменяется ее несмещенной оценкой:
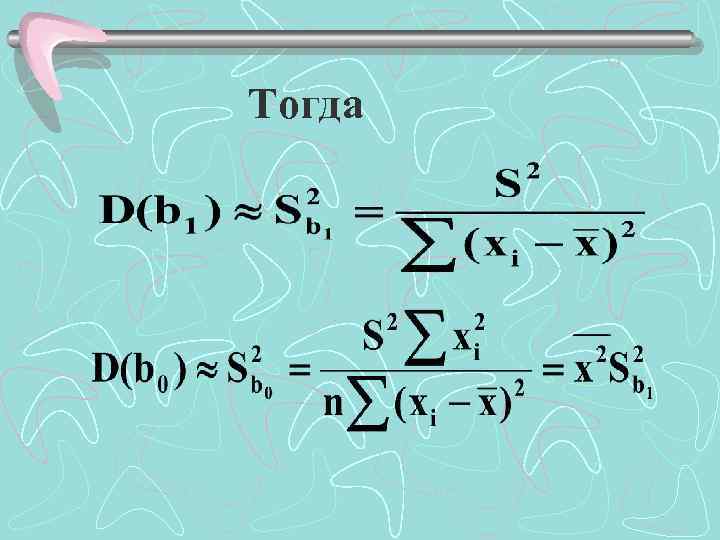
Тогда

S 2 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). Корень квадратный из необъясненной дисперсии, т. е. . называется стандартной ошибкой оценки (стандартной ошибкой регрессии).

и - стандартные отклонения случайных величин b 0, b 1, называемые стандартными ошибками коэффициентов регрессии.

Интервальные оценки коэффициентов линейного уравнения регрессии

Проверка общего качества уравнения регрессии. Коэффициент детерминации R 2 После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными.

Очевидно, если все точки лежат на построенной прямой, то регрессия Y на X «идеально» объясняет поведение зависимой переменной. В реальной жизни такая ситуация практически не встречается. Обычно поведение Y лишь частично объясняется влиянием переменной X.

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы регрессионной модели является коэффициент детерминации R 2.

В общем случае коэффициент детерминации рассчитывается по формуле:

В случае парной регрессии коэффициент детерминации будет совпадать с квадратом коэффициента корреляции, т. е. R 2=r 2.

Дробь - определяет долю разброса зависимой переменной, не объясненную регрессией Y на X. В общем случае справедливо соотношение 0<=R 2<=1.

Чем теснее линейная связь между X и Y, тем ближе коэффициент детерминации R 2 к единице. Чем слабее такая связь, тем R 2 ближе к нулю.
Парная регрессия и корреляция.ppt