КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА-3 Николай Николаевич Розанов 2014 Уравнение

КЛАССИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА-3 Николай Николаевич Розанов 2014

Уравнение Гельмгольца (монохроматическое излучение) Прямоугольная (декартова) система координат (x, y, z) – плоские волны. Цилиндрическая система координат (z, ρ, φ) – цилиндрические волны. Сферическая система координат (r, θ, φ) – сферические волны. Векторная структура поля Плоская волна (комплексная запись) Как связаны между собой Ak и k ?

Интерференция трех плоских монохроматических волн Распространяются три плоских монохроматических волны с компланарными (лежащими в одной плоскости) волновыми векторами, совпадающими частотами и поляризациями. Вещественные амплитуды волн А 1, А 2 и А 3. При каких условиях на амплитуды существуют точки в пространстве, в которых интенсивность = 0 ? (дислокации волнового фронта)

Цилиндрическая система координат Уравнение Гельмгольца Метод разделения переменных

Разделение переменных … функции Бесселя и Неймана m-го порядка Решение, конечное при

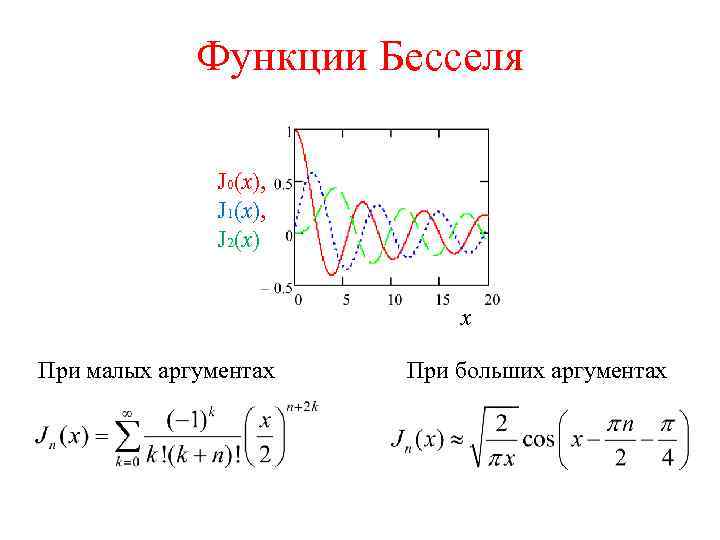Функции Бесселя J 0(x), J 1(x), J 2(x) x При малых аргументах При больших аргументах

Бесселевы пучки «Нерасходящиеся» пучки – неточно, так как их мощность бесконечна. Оптические вихри, или дислокации волнового фронта. Поляризационная структура поля: …

Поляризационная структура цилиндрических волн Суперпозиция двух линейно-независимых типов волн: поперечно-электрические волны, поперечно-магнитные волны,

Сферические волны Сферически симметричные волны … Общий случай: … Суперпозиция двух линейно-независимых полей: - «электрическая волна» , - «магнитная волна» , … Потенциал Дебая … Мощность парциальных волн бесконечна.

Геометрическая оптика Скалярное волновое уравнение

Распространение фронта э. -м. волны В начальный момент времени t = 0 э. -м. поле отлично от нуля внутри эллипсоида Определить фронт волны в момент времени t > 0. Осевая симметрия и симметрия относительно плоскости z = 0. Поэтому достаточно рассматривать плоскую задачу и z > 0. Начальная форма фронта волны - эллипс

Распространение фронта э. -м. волны Лучи с текущими координатами (ρ, z) – нормали к эллипсу в точке В момент времени t расстояние между лежащими на луче текущей точкой фронта и исходной точкой эллипса = ct: Частные случаи: