6059e5f1e5fd89b6f60e5b882023a412.ppt
- Количество слайдов: 143

King ABDUL AZIZ University Faculty Of Computing and Information Technology CPCS 222 Discrete Structures I The Foundations: Logic and Proofs Dr. Eng. Farag Elnagahy farahelnagahy@hotmail. com Office Phone: 67967 1

Propositional Logic • Propositional logic is the study of propositions (true or false statements) and The ways of combining them operators) to get new propositions (logical It is effectively an algebra of propositions. 2

Propositional Logic In this algebra, q the variables stand for unknown propositions (instead of unknown real numbers) and q the operators are and, or, not, implies, and or not implies and if and only if (rather than plus, minus, negative, times, and divided by). q. Just as middle/high school students learn the notation of algebra and how to manipulate it properly, we want to learn the notation of propositional logic and how to manipulate it properly. 3

Propositional Logic A proposition is a declarative statement that’s either true (T) or false (F), but not both Propositions § Every cow has 4 legs § Riyadh is the capital of Saudi Arabia § 1+1=2 § 2+2=3 Not Propositions § What time is it? § X+1=2 § Answer this question 4

Propositional Logic New propositions, called compound propositions are formed from existing propositions using logical Operators 5

Propositional Logic negation Suppose p is a proposition The negation of p is written as p and has meaning: “It is not the case that p. ” The proposition p is read “not P” P Truth table for the negation of proposition p p F p T T F 6

Propositional Logic negation “ today is Friday” “ it is not the case that today is Friday” or “today is not Friday” “it is not Friday today” 7

Propositional Logic conjunction Suppose p and q are propositions The conjunction of p and q is written as p q The proposition p q is read “p and q” Truth table for the Conjunction of two propositions p q p F F T T q F T p q F F F T 8

Propositional Logic conjunction p is the proposition “Today is Friday” q is the proposition “It is raining today” The conjunction of p and q is proposition “ Today is Friday and it is raining today” This proposition Is true on rainy Fridays Is false on any day that is not a Friday on Fridays when it does not rain 9

Propositional Logic disjunction § Inclusive Or Suppose p and q are propositions The disjunction of p and q is written as p q The proposition p q is read “p or q” Truth table for the Disjunction (Inclusive Or) of two propositions p q p F F T T q F T p q F T T T 10

Propositional Logic disjunction p is the proposition “Today is Friday” q is the proposition “It is raining today” The disjunction of p and q is proposition “ Today is Friday or it is raining today” This proposition Is true on any day that is either a Friday or a rainy day(including rainy Fridays) Is false on days that are not Fridays when it also does not rain 11

Propositional Logic disjunction § Exclusive Or Suppose p and q are propositions The Exclusive Or of p and q is written as p q The proposition p q is read “p or q but not both” Truth table for the Exclusive Or of two propositions p q ( p q) (p q) p F F T T q F T p q F T T F 12

Propositional Logic disjunction § Exclusive Or “Tonight I will stay home or go out to a movie. ” movie 13

Propositional Logic implication Suppose p and q are propositions The conditional statement (implication) p q implication The proposition p q is read “ if p, then q” q P hypothesis – antecedent – premise q conclusion -consequence Truth table for the Implication p q p q p F F T T q F T p q T T F T 14

Propositional Logic implication Terminology used to express p q “if p, then q” “p is sufficient for q” “q if p” “q when p” “a necessary condition for p is q” “q unless p“ “p implies q” “p only if q” “a sufficient condition for q is p” “q whenever p” “q is necessary for p” “q follows from p” “if p, q” 15

Propositional Logic implication p is the proposition “Ahmed learns discrete mathematics” q is the proposition “Ahmed will find a good job” The p q is proposition “ if Ahmed learns discrete mathematics, then he will find a good job” This proposition Is false when p is true and q is false Otherwise it is true 16

Propositional Logic implication p is the proposition “today is Friday” q is the proposition “ 2+3=5” The p q is proposition “ if today is Friday, then 2+3=5” This proposition Is true because its Conclusion (q) is true “ p F F T T q F T p q T T F T 17

Propositional Logic implication p is the proposition “today is Friday” q is the proposition “ 2+3=6” The p q is proposition “ if today is Friday, then 2+3=6” This proposition Is true every day except Friday p F F T T q F T p q T T F T 18

Propositional Logic implication The conditional statement (implication) p q “if it is raining, then the home team wins” q p is called contrapositive of p q “if the home team does not win, then it is not raining” The proposition q p is called converse of p q “if the home team wins, then it is raining” p q is called inverse of p q “if it is not raining, then the home team does not win” 19

Propositional Logic bi-implication Suppose p and q are propositions The biconditional statement (bi-implication) p q bi-implication The proposition p q is read “ p if and only if q” q p q is true if both p q q p are true p q ------- p q Truth table for the Bi-implication p q (p q ) ( p q ) p F F T T q F T p q T F F T 20

Propositional Logic bi-implication The proposition p q has the same truth value as p q q p p q p q q p F F T T p q q p T p q T F T F F T T T 21

Propositional Logic bi-implication p is the proposition “You can take the flight” q is the proposition “You buy a ticket” The p q is proposition “You can take the flight if and only if You buy a ticket” This proposition Is true if p and q are either both true or both false” 22

Propositional Logic Truth table of compound propositions § Precedence of logical operators 23

Propositional Logic Truth table of compound propositions Construct the Truth table of compound propositions (p q) (p q) p F F T T q q p q F T T T F F F T T T F T p q (p q) F F F T F T 24

Propositional Logic § Translating English sentence into a logical expression “You can access the internet from campus only if you are a computer science major or you are not a freshman” a: “You can access the internet from campus” b: “you are a computer science major” c: “you are a freshman” Where a, b, c are propositional variables a (b c) 25

Propositional Logic § Translating English sentence into a logical expression (System specifications) ü Translating sentences in natural language into logical expressions is an essential part of specifying both hardware and software systems. üSystem and software engineers take requirements in natural language and produce precise and unambiguous specifications that can be used as the basis for system development. 26

Propositional Logic § Translating English sentence into a logical expression (System specifications) ü Express the specification ”The automated reply cannot be sent when the file system is full“ using logical connectives. P: “The automated reply can be sent” q: “The file system is full” q p üSystem specifications should be consistent They should not contain conflicting requirements that could be used to drive a 27 contradiction

Propositional Logic § Translating English sentence into a logical expression (System specifications) determine whether these system specifications are consistent : ü “The diagnostic message is stored in the buffer or it is retransmitted” ü “The diagnostic message is not stored in the buffer” ü “if the diagnostic message is stored in the buffer, then it is retransmitted” P: “The diagnostic message is stored in the buffer” q: “The diagnostic message is retransmitted” p q p p q 28

Propositional Logic § Translating English sentence into a logical expression (System specifications) p q p p q p F F T T q p F T T T F F T F p q p q F T T T F T system specifications are consistent 29

Propositional Logic § Translating English sentence into a logical expression (System specifications) determine whether these system specification are consistent : ü “The diagnostic message is stored in the buffer or it is retransmitted” ü “The diagnostic message is not stored in the buffer” ü “if the diagnostic message is stored in the buffer, then it is retransmitted” ü “The diagnostic message is not retransmitted” P: “The diagnostic message is stored in the buffer” q: “The diagnostic message is retransmitted” p q p p q q 30

Propositional Logic § Translating English sentence into a logical expression (System specifications) p q p p q q p F F T T q p F T T T F F T F p q p q F T T T F T q T F system specifications are inconsistent 31

Propositional Logic § Boolean Searches Logical connectives are used extensively in searches of large collections of information: Indexes of Web pages, these searches employ techniques from propositional logic. The connective AND is used to match records that contain both of the two search items. OR is used to match one or both of two search items. NOT is used to exclude a particular search 32 item (- is used in Google).

Propositional Logic § Logic Puzzles puzzles that can be solved using logical reasoning are known as logic puzzles. Knight “always tell the truth” Knave “always lie” You encounter two people A and B, What are A and B if A says “B is a knight” B says “ the two of us are opposite” 33

Propositional Logic § Logic Puzzles Let: p: “A is a knight“ q: “B is a knight“ p : “ A is a knave” q: “ B is a knave” A says “B is a knight” q B says “ the two of us are opposite” (p q) ( p q) If A is a knight Then q is true and (p q) ( p q) is true But (p q) ( p q) is false We can conclude that A is a knave 34

Propositional Logic § Logic Puzzles Let: p: “A is a knight“ q: “B is a knight“ p : “ A is a knave” q: “ B is a knave” A says “B is a knight” q B says “ the two of us are opposite” (p q) ( p q) If B is a knight (q is true) Then (p q) ( p q) is true and q is false We can conclude that B is a knave A and B are knaves 35

Propositional Logic § Logic and Bit operations A bit string is a sequence of zero or more bits. The length of this string is the number of bits in the string. 101010011 is a bit string of length nine § Bitwise OR( ), Bitwise AND ( ), Bitwise XOR( ) 0 1 1 0 0 0 1 1 1 0 1 Bitwise OR 1 1 1 0 1 1 1 Bitwise AND 0 1 0 0 Bitwise XOR 1 0 1 0 1 1 36

Chapter 1 Exercises Pages (16 -20) 1, 3, 6, 7, 9, 10 12 -14 (b, c) 15, 17 20, 22, 24, 25, 26 27 -33 (e) 36 -38 48 50 37

Propositional Equivalences Classification of compound propositions §A compound proposition that is always true is called a tautology. (p p) §A compound proposition that is always false is called a contradiction. (p p) §A compound proposition that is neither a tautology nor a contradiction is called a contingency. 38

Propositional Equivalences Logical equivalences compound propositions that have the same truth values in all possible cases are called Logically equivalent Compound propositions p and q are Logically equivalent if p q is a tautology. logical equivalence Note and are not logical operators(connectives). Rather they indicate a kind of logical equality. 39
![Propositional Equivalences Prove that [r (q ( r p ))] r (p q) by Propositional Equivalences Prove that [r (q ( r p ))] r (p q) by](https://present5.com/presentation/6059e5f1e5fd89b6f60e5b882023a412/image-40.jpg)
Propositional Equivalences Prove that [r (q ( r p ))] r (p q) by using a truth table. 40

Propositional Equivalences Identity laws Domination laws Idempotent laws Double negation law p T p p F F p T T p p p ( p) p Negation laws p p T p p F Absorption laws p (p q) p p (p q) p Commutative laws p q q p Associative laws (p q) r p (q r) De Morgan’s laws (p q) p q Distributive laws p (q r) (p q) (p r) T denotes the compound proposition that is always true F denotes the compound proposition that is always false 41

Propositional Equivalences p q (p q) p q q p p q (p q) (p q) (p r) p (q r ) (p r) (q r) (p q ) r p p p (p q (p q) (q p) q p q q (p q ) ( p q ) q) p q 42

Propositional Equivalences Use De Morgan’s of “Ahmed has a p: “Ahmed has a q: “Ahmed has a law to express the negation mobile and he has a laptop” mobile” laptop” p q (p q) p q p: “Ahmed has not a mobile” q: “Ahmed has not a laptop” “Ahmed has not a mobile or he has not a laptop” 43

Propositional Equivalences Show that (p q) p q Show that (p ( p q)) p q Show that (p q) is a tautology 44

Chapter 1 Exercises Pages (28 -30) 1(a, b, f) 4(b) 7, 8 9(a, f) 11(a, f) 15 26, 27 45

Predicates and Quantifiers Predicates “x is greater than 3” This statement is neither true nor false when the value of the variable is not specified. This statement has two pats The fist part (subject) is the variable x The second (predicate) is “is greater than 3” We can denote this statement by P(x) Where P denotes the predicate “is greater than 3” Once a value has been assigned to x, the statement P(x) becomes a proposition and has a truth value. P is called Proposition function. 46

Predicates and Quantifiers Predicates let P(x) denote “is greater than 3” What are the truth values of P(4) and P(2)? let Q(x, y) denote “x=y+3” What are the truth values of Q(1, 2) and Q(3, 0)? let R(x, y, z) denote “x+y=z” What are the truth values of R(1, 2, 3) and R(0, 0, 1)? P(x 1, x 2, x 3, ………, xn) P is called n-place(n-ary) predicate. 47

Predicates and Quantifiers Predicates let A(c, n) denote “computer c is connected to network n” Suppose that the computer MATH 1 is connected to network CAMPUS 2, but not to network CAMPUS 1 What are the truth values of A(MATH 1, CAMPUS 1) and A(MATH 1, CAMPUS 2) ? 48

Predicates and Quantifiers Predicates Proposition functions(Predicates) occur in computer programs. If x>0 then x: =x+1 P(x) : “x>0” If P(x) is true the assignment is executed If P(x) is false the assignment is not executed 49

Predicates and Quantifiers Universal quantification Which tell us that a predicate is true for every element under consideration. existential quantification Which tell us that there is one or more element under consideration for which the predicate is true. The area of logic that deals with predicates and quantifiers is called predicate calculus. 50

Predicates and Quantifiers The universal quantification of P(x) is the statement “P(x) for all values of x in the domain” ∀ x P(x) read as “for all x P(x)” “for every x P(x)” ∀ is called universal quantifier The existential quantification of P(x) is the statement “there exists an element x in the domain such that P(x)” ∃x P(x) read as “there is an x such that P(x)” “there is at least one x such that P(x)” “for some x P(x)” 51 ∃ is called existential quantifier

Predicates and Quantifiers ∀ x P(x) When true P(x) is true for every x. When false there is an x for which P(x) is false. ∃x P(x) When true there is an x for which P(x) is true. When false P(x) is false for every x. 52

Predicates and Quantifiers Let Q(x) “x<2” What is the truth value of ∀ x Q(x) when the domain consists of all real numbers? Q(x) is not true for every real number x, for example Q(3) is false. x=3 is a counterexample for the statement ∀ x Q(x) Thus ∀ x Q(x) is false. 53

Predicates and Quantifiers Let Q(x) “x 2>0” What is the truth value of ∀ x Q(x) when the domain consists of all integers? Q(x) is not true for every integer number x, for example Q(0) is false. x=0 is a counterexample for the statement ∀ x Q(x) Thus ∀ x Q(x) is false. 54

Predicates and Quantifiers What is the truth value of ∀ x (x 2 x) when the domain a) consists of all real number? b) consists of all integers? a) is false because (0. 5)2 0. 5 x 2 x is false for all real numbers in the range 0<x<1 b) is true because there are no integer x with 0<x<1 55

Predicates and Quantifiers Let Q(x) “x>3” What is the truth value of ∃x Q(x) when the domain consists of all real numbers? Q(x) is sometimes true , for example Q(4) is true. Thus ∃x Q(x) is true. ∃x Q(x) is false iif there is no elements in the domain for which Q(x) is true. 56

Predicates and Quantifiers Let Q(x) “x=x+1” What is the truth value of ∃x Q(x) when the domain consists of all real numbers? Q(x) is false for every real number. Thus ∃x Q(x) is false iif there is no elements in the domain for which Q(x) is true or the domain is empty. 57

Predicates and Quantifiers When all the elements in the domain can be listed x 1, x 2 , x 3, x 4, ……. , xn ∀ x Q(x) is the same as the conjunction Q(x 1) Q(x 2) …. Q(xn) ∃x Q(x) is the same as the disjunction Q(x 1) Q(x 2) …. Q(xn) 58

Predicates and Quantifiers Let Q(x) “x 2<10” What is the truth value of ∀ x Q(x) when the domain consists of the positive integers not exceeding 4? ∀ x Q(x) is the same as the conjunction Q(1) Q(2) Q(3) Q(4) is false Thus ∀ x Q(x) is false. 59

Predicates and Quantifiers Let Q(x) “x 2>10” What is the truth value of ∃x Q(x) when the domain consists of the positive integers not exceeding 4? ∃x Q(x) is the same as the disjunction Q(1) Q(2) Q(3) Q(4) is true Thus ∃x Q(x) is true. 60

Predicates and Quantifiers If domain consists of n (finite) object and we need to determine the truth value of ∀ x Q(x) § Loop through all n values of x to see if Q(x) is always true § If you encounter a value x for which Q(x) is exit the loop with ∀ x Q(x) is false § otherwise ∀ x Q(x) is true false, ∃x Q(x) § Loop through all n values of x to see if Q(x) is true § If you encounter a value x for which Q(x) is true, exit the loop with ∃x Q(x) is true § Otherwise ∃x Q(x) is false 61

Predicates and Quantifiers You can define other quantifiers, for example “there are exactly two” “there at least 100” Uniqueness quantifier ∃! ∃1 “there exists a unique x such that P(x) is true” “there is exactly one” “there is one and only one” Precedence of quantifiers ∀ ∃ have higher precedence than all logical operators 62

Quantifiers with restricted domain What do these statements mean (domain real) §∀ x<0 (x 2>0) same as ∀ x (x<0 x 2>0) “the square of a negative real number is positive” §∀ y 0 (y 3 0) same as ∀ y(y 0 y 3 0) “the cube of every nonzero real number is nonzero” §∃ z >0 (z 2=2) same as ∃ z(z>0 z 2=2) “there is a positive square root of 2” 63

Binding variables §∃ x (x+y=1) The variable x is bounded by the existential quantification ∃ x and the variable y is free §∃ x (P(x) Q(x)) ∀ x R(x) All variables are bounded The scope of the first quantifier ∃ x is the expression P(x) Q(x) second quantifier ∀ x is the expression R(x) existential quantifier binds the variable x in P(x) Q(x) Universal quantifier binds the variable x in R(x) 64

Logical equivalence involving quantifiers Statements involving predicates and quantifier are logically equivalent iff they have the same truth value Show that ∀ x (P(x) Q(x)) ∀ x P(x) ∀ x Q(x) § suppose that ∀ x (P(x) Q(x)) is true, this means that if a is in the domain then P(a) Q(a) is true Hence, both P(a) and Q(a) are true for every element in the domain 65 So ∀ x P(x) and ∀ x Q(x) are both true.

Logical equivalence involving quantifiers Show that ∀ x (P(x) Q(x)) ∀ x P(x) ∀ x Q(x) § suppose that ∀ x P(x) ∀ x Q(x) is true, it follows that both ∀ x P(x) and ∀ x Q(x) are true hence, if a is in the domain then P(a) is true and Q(a) is true This means that ∀ x (P(x) Q(x)) is true. Now we can conclude that ∀ x (P(x) Q(x)) ∀ x P(x) ∀ x Q(x) 66

Logical equivalence involving quantifiers ∀ x (P(x) Q(x)) ∀ x P(x) ∀ x Q(x) The universal quantifier can be distributed over the a conjunction ( ). The universal quantifier can be distributed over the a disjunction ( ). The existential quantifier can not be distributed over the a conjunction ( ) and disjunction ( ). 67

Negating quantified expression “Every student in your class has taken a course in calculus” ∀ x P(x) Where, P(x) is “x has taken a course in calculus” and the domain consists of the student in your class Negation “It is not the case that every student in your class has taken a course in calculus” or “There is a student in your class who has not taken a course in calculus” ∃ x P(x) ∀ x P(x) ∃ x P(x) 68

Negating quantified expression “There is a student in this class who has taken a course in calculus” ∃ x Q(x) Where, Q(x) is “x has taken a course in calculus” and the domain consists of the student in your class Negation “It is not the case that there is a student in this class who has taken a course in calculus” or “Every student in this class has not taken a course in calculus” ∀ x Q(x) “Not all students in this class have taken a course in calculus” is not 69 used. ∃ x Q(x) ∀ x Q(x)

Negating quantified expression Show that (homework) § ∀ x P(x) ∃ x P(x) § ∃ x P(x) ∀ x P(x) 70

Negating quantified expression De Morgan’s laws for quantifiers ∃ x P(x) ∀ x P(x) The negation is true when for every x, P(x) is false The negation is false when there is an x for which P(x) is true ∀ x P(x) ∃ x P(x) The negation is true when there is an x for which P(x) is false The negation is false when for every x, P(x) is true 71

Negating quantified expression De Morgan’s laws for quantifiers When the domain of a predicate Q(x) consists of n elements x 1, x 2 , x 3, x 4, ……. , xn ∀ x Q(x) is the same as the conjunction Q(x 1) Q(x 2) …. Q(xn) ∀ x Q(x) is the same as the disjunction Q(x 1) Q(x 2) …. Q(xn) ∃x Q(x) is the same as the disjunction Q(x 1) Q(x 2) …. Q(xn) ∃x Q(x) is the same as the conjunction Q(x 1) Q(x 2) …. Q(xn) 72

Negating quantified expression Examples: what are the negation of §∀ x (x 2>x) §∃x (x 2=x) §∀ x (x 2>x) ∃x (x 2 x) §∃x (x 2=x) ∀ x (x 2 x) 73
![Negating quantified expression Show that ∀ x [P(x) Q(x)] ∃x [P(x) Q(x)] ∀ x Negating quantified expression Show that ∀ x [P(x) Q(x)] ∃x [P(x) Q(x)] ∀ x](https://present5.com/presentation/6059e5f1e5fd89b6f60e5b882023a412/image-74.jpg)
Negating quantified expression Show that ∀ x [P(x) Q(x)] ∃x [P(x) Q(x)] ∀ x [P(x) Q(x)] ∃x ∃x [P(x) Q(x)] [ P(x) Q(x)] [P(x) Q(x)] 74

Translating from English into Logical Expressions Express the statement “Every student in the class has studied calculus” using predicates and quantifiers. § Rewrite the statement to identify the appreciate quantifiers to use “For every student in the class, that student has studied calculus” §Introduce the variable x “For every student x in the class, x has studied calculus” § introduce C(x) “x has studied calculus” ∀ x C(x) The domain for x consists of the students in the class 75

Translating from English into Logical Expressions If we change the domain to consists of people “For every person x, if person x is a student in the class, then x has studied calculus” C(x) “x has studied calculus” S(x) “person x is a student in the class” ∀ x (S(x) C(x)) Note ∀ x (S(x) C(x)) is wrong All people are students in this class and have 76 studied calculus

Translating from English into Logical Expressions Express the statements “some students in the class has visited Cairo” , “every student in the class has visited either Aswan or Cairo ” using predicates and quantifiers. § “some students in the class has visited Cairo” some students ~ there is a student C(x) “x has visited Cairo” ∃ x C(x) § “every student in the class has visited either Aswan or Cairo ” A(x) “x has visited Aswan ” ∀ x (C(x) A(x)) 77

Translating from English into Logical Expressions System specifications Express the statement “Every mail message larger than one megabyte will be compressed” using predicates and quantifiers. S(m, y) “Mail message m is larger than y megabyte” Where m has the domain of all mail message y is a positive real number C(m) “Mail message m will be compressed” ∀ m (S(m, 1) C(m)) 78

Translating from English into Logical Expressions System specifications Express the statement “If a user is active, at least one network link will be available” using predicates and quantifiers. A(u) “user u is active” Where u has the domain of all users S(n, x) “network link n is in state x” Where n has the domain of all network links x has the domain of all possible states for a network link ∃ u A(u) ∃ n S(n, available) 79

Chapter 1 Exercises Pages (46 -50) 1 -4 5(a, d) 8(b, c) 10 12(b, d, g) 17 20(e) 21 -22 24, 29, 31 , 36 40 -42 43, 48 80

Nested Quantifiers Two quantifiers are nested if one is within the scope of the other. ∀ x∃ y (x+y=0) Every thing within the scope of a quantifier can be thought as a propositional function. For example ∀ x Q(x) is ∃ y P(x, y) is (x+y=0) 81

Nested Quantifiers Translate into English ∀ x∀ y( (x>0) (y<0) (xy<0)) The domain of both x and y are real number. Thinking of quantification as a loops ∀ x∀ y P(x, y) ∀ x ∃ y P(x, y) For all x For all y P(x, y) all are true End for all y for all x and y End for all x at least one is true in y loop and all x 82

Nested Quantifiers Thinking of quantification as a loops ∃ x ∀ y P(x, y) For all y For all x P(x, y) at least one is true in x loop and all y End for all x End for all y ∃ x∃ y P(x, y) For all x For all y P(x, y) at least one is true End for all y End for all x 83

Nested Quantifiers The order of quantifiers Suppose that the universe for x and y is {1, 2, 3}. Also, assume that P(x, y) is a predicate that is true in the following cases, and false otherwise: P(1, 3), P(2, 1), P(2, 2), P(3, 1), P(3, 2), P(3, 3). Determine whether each of the following is true or false: (a) ∀ y∃ x (x y ∧ P(x, y)). (b) ∀ x∃ y (x y ∧ ¬P(x, y)). (c) ∀ y∃ x (x y ∧ ¬P(x, y)). true False. 84

Nested Quantifiers Translate the following statements into logical expression § “the sum of two positive integers is always positive” Or ∀ x∀ y( (x>0) (y>0) (x+y>0)) ∀ x∀ y(x+y>0), where the domain of both x and y consists of all positive integers. §“every real number except zero has a multiplicative inverse” ∀ x ( (x 0) ∃ y(xy=1)) 85

Nested Quantifiers Translate the statements into English § ∀ x(C(x) ∃ y(C(y) F(x, y) )) where C(x) is “x has a computer” F(x, y) is “x and y are friends” the domain for both x and y consists of all student in your school. “for every student x in your school, x has a computer or there is a student y such that y has a computer and x and y are friends ” “every student in your school has a computer or has a friend who has a computer” 86

Nested Quantifiers Express the statement as logical expression (quantifiers, predicates, logical connectives) the domain consists of all people. § “ if a person is male and is a parent, then this person is someone’s father” ∀ x( (M(x) P(x)) ∃ y F(x, y) ) where M(x) is “x is male ” P(x) is “x is a parent” F(x, y) is “x is the father of y” Or ∀ x ∃ y ( (M(x) P(x)) F(x, y) ) 87

Negating Nested Quantifiers Negate this statement( no negation precedes a quantifier) ∀ x ∃ y (xy=1) (∀ x ∃ y (xy=1)) ∃ x ∃ y (xy=1) ∃ x ∀ y (xy 1) 88

Chapter 1 Exercises Pages (58 -62) 1 4 6 11 24 26 29 31 39 45 89

Rules of Inference 90
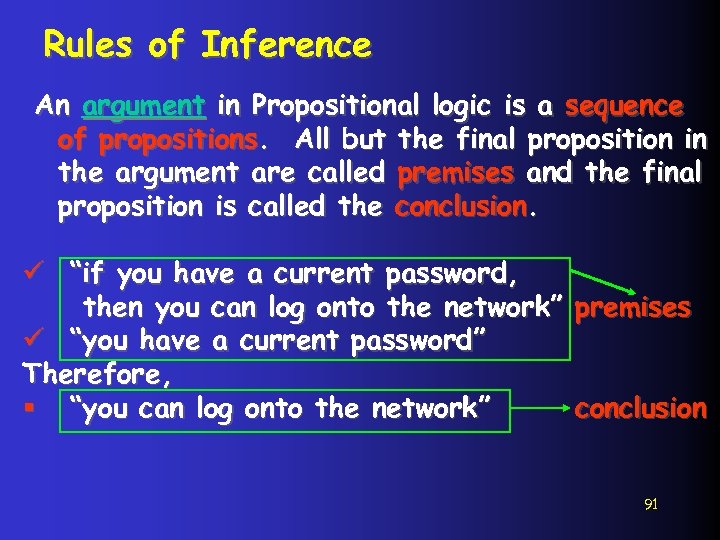
Rules of Inference An argument in Propositional logic is a sequence of propositions. All but the final proposition in the argument are called premises and the final proposition is called the conclusion. ü “if you have a current password, then you can log onto the network” premises ü “you have a current password” Therefore, § “you can log onto the network” conclusion 91

Rules of Inference An argument form in Propositional logic is a sequence of compound propositions involving propositional variables. p ü “if you have a current password, then you can log onto the network” q ü “you have a current password” Therefore, § “you can log onto the network” p q 92

Rules of Inference Valid arguments in Propositional logic An argument is valid if the truth of all its premises implies that the conclusion is true. If we have an argument with premises p 1, p 2, p 3, …………, pn and conclusion q This argument is valid when (p 1 p 2 p 3 ………… pn) q is a tautology 93

Rules of Inference We can use a truth table to show that an argument form is valid. By showing that whenever the premises are true, the conclusion must also be true. p q p F F T T q F T p q (p q) p (p (p q)) q (p (p T F T F F T T 94

Rules of Inference We can use a truth table to argument form is valid. By whenever the premises are must also be true. show that an showing that true, the conclusion If an argument form involves 10 different propositional variables, to use truth table, 210=1024 rows are needed. This is a tedious(long and boring) approach. 95

Rules of Inference instead of using a truth table to show that an argument form is valid, we cant use Rules of inference. The tautology (p (p q)) q is the basis of the (p rule of inference called Modus Ponens ( or law of detachment- mode that affirms) p q The hypotheses are written in a column, followed by horizontal bar, followed by the and the conclusion. 96

Rules of Inference Modus Ponens p p q q Modus Ponens tell us that if a conditional statement and its hypothesis are both true, then the conclusion must also be true. 97

Rules of Inference Modus Ponens conditional statement “if you have a current password, then you can log onto the network” hypothesis “you have a current password” if conditional statement and hypothesis are true Then the conclusion is true “you can log onto the network” 98

Rules of Inference Modus Ponens (Example) “if , then “ § Determine whether the argument is valid, and determine whether its conclusion must be true because of the validity of the argument. Let p be the proposition and q be the proposition the premises of the argument are p q and p and its conclusion is q. 99

Rules of Inference Modus Ponens (Example) “if , then “ the premises of the argument are p q and p and its conclusion is q. this argument is valid (it is constructed by using Modus ponens), a valid argument form. The premise is false, therefore we can not conclude that the conclusion is true. Conclusion is false. 100

Rules of Inference Rule – general form Pattern establishing that if we know that a set of hypotheses are all true, then a certain related conclusion statement is true. Hypothesis 1 Hypothesis 2 … conclusion “ ” means “therefore” 101

Rules of Inference Rule – general form Each logical inference rule corresponds to an implication that is a tautology. Hypothesis 1 Hypothesis 2 … conclusion Inference rule Corresponding tautology: 102 ((Hypoth. 1) (Hypoth. 2) …) conclusion

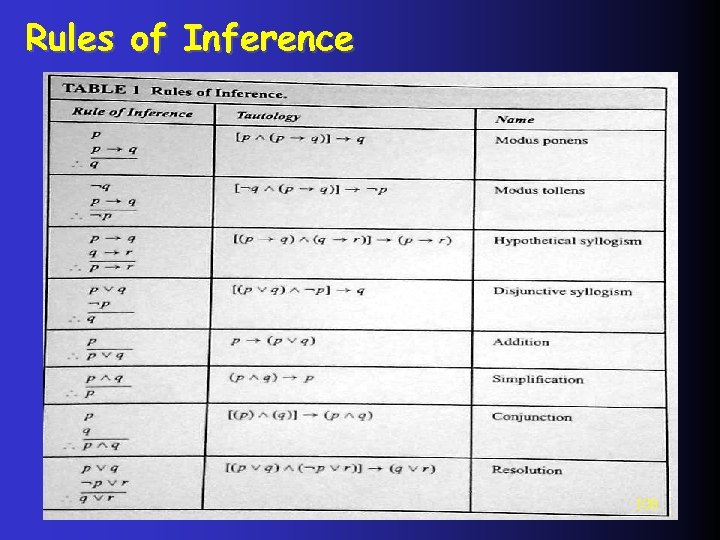
Rules of Inference Some Inference Rules p Rule of Addition p q “It is below freezing now. Therefore, it is either below freezing or raining now. ” p q Rule of Simplification p “It is below freezing and raining now. Therefore, it is below freezing now. ” 103

Rules of Inference p q Rule of Conjunction “It is below freezing. It is raining now. Therefore, it is below freezing and it is raining now. ” 104

Rules of Inference p p q q Rule of modus ponens (law of detachmentthe mode of affirming) “If it is snows today, then we will go skiing”. “It is snowing today”. Therefore (or imply that) “We will go skiing” q p q p Rule of modus tollens (mode of denying) 105

Rules of Inference p q Rule of disjunctive syllogism p q q r p r Rule of hypothetical syllogism 106

Rules of Inference p q p r q r Rule of Resolution 107
Rules of Inference 108

Rules of Inference Examples State which rule of inference is the basis of the following argument: § “it is below freezing now (p). Therefore, it is either below freezing or raining now (q). ” this argument is of the form p p q This argument uses the addition rule 109

Rules of Inference Examples State which rule of inference is the basis of the following argument: § “it is below freezing now(p) and raining now(q). Therefore, it is below freezing now. ” this argument is of the form p q p This argument uses the simplification rule 110

Rules of Inference Examples State which rule of inference is the basis of the following argument: § if it rains today(p), then we will not have a barbecue today(q). if we do not have a barbecue today, then we will have a barbecue tomorrow(r). Therefore, it is rains today, then we will have a barbecue tomorrow. this argument is of the form p q q r p r This argument uses the hypothetical syllogism 111 rule

Using Rules of Inference to Build Arguments § A formal proof of a conclusion C, given premises p 1, p 2, …, pn consists of a sequence of steps, each of which applies some inference rule to premises or to previously-proven statements (as hypotheses) to yield a new true statement (the conclusion). • A proof demonstrates that if the premises are true, then the conclusion is true (i. e. , valid argument). 112

Using Rules of Inference to Build Arguments § Example: Show that the hypotheses “It is not sunny and it is cold (q). ” “we will swim (r) only if it is sunny (p), “If we do not swim, then we will canoe(s). ” “If we canoe, then we will be home early(t). ” Leads to the conclusion “We will be home early” t p q , r p, r s, s t 113

Using Rules of Inference to Build Arguments § Example: (we can use the truth table) Premises p q , r p, r s, s t Conclusion t Step Reason 1. p q Hypothesis 2. p Simplification using (1) 3. r p Hypothesis 4. r Modus Tollens using (2) (3) 5. r s Hypothesis 6. s Modus ponens using (4) (5) 7. s t Hypothesis 114 8. t Modus ponens using (6) (7)

Common Fallacies Is this argument is valid? If you do every problem in this book, then you will learn discrete mathematics(q). You learned discrete mathematics. ” Therefore, you did every problem in this book(p). this argument is of the form p q and q then p. This is an example of an incorrect argument using the Fallacy of affirming the conclusion: p q and q does not imply p The proposition [(p q) q) p] is not a tautology (its false (p if p is F and q is T) You can learn discrete mathematics in some way other than doing every problem in this book (by readinglistening to lectures-doing some(but not all) the problems in this book ) 115

Common Fallacies Is this argument is valid? If you do every problem in this book(p), then you will learn discrete mathematics(q). you did not do every problem in this book. Therefore, You did not learn discrete mathematics. ” this argument is of the form p q and p imply q. This is an example of an incorrect argument using the Fallacy of denying the hypothesis : p q and p does not imply q The proposition [(p q) p) q] is not a tautology (its (p false if p is F and q is T) It is possible that you learned discrete even you did not do every problem in this book 116

Common Fallacies • A fallacy is an inference rule or other proof method that is not logically valid. – May yield a false conclusion! • Fallacy of affirming the conclusion: – “p q is true, and q is true, so p must be true. ” (No, because F T is true. ) • Fallacy of denying the hypothesis: – “p q is true, and p is false, so q must be false. ” (No, again because F T is true. ) 117

Inference Rules for Quantifiers § Universal instantiation x P(x) P(c) (substitute any object c) We can conclude that P(c) is true, where c is a particular member of the domain, if we know that x P(x) is true. Example “all students have internet account” “Ahmed has internet account” Where, Ahmed is a member of the domain 118 Of all students

Inference Rules for Quantifiers • Existential instantiation x P(x) P(c) (for some element c) We can conclude that there is an element c in the domain for which P(c) is true, if we know that x P(x) is true. 119

Inference Rules for Quantifiers • Universal generalization • P(c) (for an arbitrary c) x P(x) • Existential generalization • P(c) x P(x) (for some element c ) 120

Inference Rules for Quantifiers Show that the premises “Everyone in this discrete math class has taken a course in computer science” and “Ali is a student in this class” imply the conclusion “Ali has taken a course in computer science” D(x): “x is in discrete math class” C(x): “x has taken a course in computer science” x (D(x) C(x)) Premise #1 D(Ali) Premise #2 C(Ali) Step 1. x (D(x) C(x)) 2. D(Ali) C(Ali) 3. D(Ali) 4. C(Ali) Reason Premise #1 Univ. instantiation. Premise #2. Modus ponens on 2, 3. 121

Inference Rules for Quantifiers Show that the premises “A student in this class has not read the book” and “Everyone in this class passed the first exam” imply the conclusion “Someone who passed the first exam has not read the book” C(x): “x is in this class” x(C(x) B(x)) B(x): “x has read the book” x (C(x) P(x)) P(x): “x passed the first exam” x(P(x) B(x)) Step Reason 1. x(C(x) B(x)) Premise #1. 2. C(a) B(a) Exist. instantiation. 3. C(a) Simplification on 2. 4. x (C(x) P(x)) Premise #2. 5. C(a) P(a) Univ. instantiation. 6. P(a) Modus ponens on 3, 5 7. B(a) Simplification on 2 8. P(a) B(a) Conjunction on 6, 7 9. x(P(x) B(x)) Exist. generalization 122

Combining Rules of Inference for Propositions and Quantified Statements Universal Modus Ponens Inference Rule x (P(x) Q(x)) P(a) Q(a) Universal Modus Tollens Inference Rule x (P(x) Q(x)) Q(a) P(a) Where a is a particular element in the domain 123

Combining Rules of Inference for Propositions and Quantified Statements Assume that “For all positive integers n, if n is greater than 4, then n 2 is less than 2 n” is true. Use universal modus ponens to show that 1002 < 2100 P(n) denote “n>4” Q(n) denote “n 2 < 2 n” n (P(n) Q(n)) P(100) is true, because 100>4 It follows by universal modus ponens that Q(n) is true, this means that n 2 < 2 n is true 1002 < 2100 is true 124

Exercises pp(72 -74) 1 -3 6 -9 12 -13 15 17 -19 24 -25 27 29 33 125

Introduction to Proofs Some terminology Theorem Is a statement that can be shown to be true. Axioms (postulates) Statements that used in a proof and are assumed to be true. 126

Proof Methods Proving p q Direct proof: Assume p is true, and prove q. Indirect proof: Assume q, and prove p. Trivial proof: Prove q true. Vacuous proof: Prove p is true. 127

Proof Methods (Direct proof) § Proving p q Direct proof: Assume p is true, and prove q Definition: The integer n is even if there exists an integer k such that n=2 k, and n is odd if there exists an integer k such that n=2 k+1. Axiom: Every integer is either odd or even. Theorem: (For all numbers n) If n is an odd integer, then n 2 is an odd integer. Proof: If n is odd, then n = 2 k+1 for some integer k. Thus, n 2 = (2 k+1)2 = 4 k 2 + 4 k + 1 = 2(2 k 2 + 2 k) + 1. Therefore n 2 is of the form 2 j + 1 (with j the integer 2 k 2 + 2 k), thus n 2 is odd. 128

Proof Methods (Direct proof) § Proving p q Direct proof: Assume p is true, and prove q Direct proofs lead from the hypothesis of a theorem to the conclusion. They begin with the premises, continue with a sequence of deductions, and ends with the conclusion. A direct proof often reach dead ends. Example Prove that if n is an integer and 3 n+2 is odd, then n is odd. We assume that 3 n+2 is an odd This mean that 3 n+2=2 k+1 There is no direct way to proof integer that n is odd integer 129

Proof Methods (Indirect proof) § Proving p q Indirect proof(proof by contraposition): Assume q, and prove p. Contraposition (p q q p) Example Prove that if n is an integer and 3 n+2 is odd, then n is odd. Proof: Suppose that the conclusion is false, i. e. , that n is even. Then n=2 k for some integer k. Then 3 n+2 = 3(2 k)+2 = 6 k+2 = 2(3 k+1). Thus 3 n+2 is even, because it equals 2 j for integer j = 3 k+1. So 3 n+2 is not odd. We have shown that ¬(n is odd)→¬(3 n+2 is odd), thus its contraposition (3 n+2 is odd) → (n is odd) is also 130 true.

Proof Methods (Indirect proof) § Proving p q Indirect proof(proof by contraposition): Assume prove p is true. Contraposition (p q q q, and p) Example Prove that if n=ab, where a and b are positive integers, then a (n)1/2 or b (n)1/2 We assume that a (n)1/2 b (n)1/2 is false This implies that both a (n)1/2 and b (n)1/2 are false This implies that a > (n)1/2 and b > (n)1/2 This implies that ab> (n)1/2 Then ab>n This show that ab n theorem is proved 131

Proof Methods (Vacuous proof) Proving p q Vacuous proof: Prove p is true. Examples Theorem: (For all n) If n is both odd and even, then n 2 = n + n. Proof: The statement “n is both odd and even” is necessarily false, since no number can be both odd and even. So, theorem is vacuously true. 132

Proof Methods (Trivial proof) Proving p q Trivial proof: Prove q true. Examples Theorem: (For integers n) If n is the sum of two prime numbers, then either n is odd or n is even. Proof: Any integer n is either odd or even. So the conclusion of the implication is true regardless of the truth of the hypothesis. Thus the implication is true trivially. 133

Proof Methods (Example) Definition: The real number r is rational if there exist integers p and q with q≠ 0 such that r=p/q. A real number that is not rational is called irrational. Theorem: Prove that the sum of two rational numbers is rational. Proof: assume that r and s are rational numbers r=p/q and s=t/u where p, q, t, u are integers and p≠ 0, u≠ 0 r+s=(p/q)+(t/u) = (pu+qt)/(qu) Because p≠ 0 and u≠ 0 , then qu≠ 0 Both (pu+qt) and (qu) are integers Then theorem is proved Note that : Our attempt to find direct proof succeeded. 134

Proof Methods (Proof by Contradiction) ( • Proving p is true Assume we can find a contradiction q such that ( p q) is true. Because q is false and ( p q) is true, we can conclude that p is false, which means that p is true. p, and prove that p (r r) is a trivial contradiction, equal to F Thus p F is true only if p=F P is true 135

Proof Methods (Proof by Contradiction) ( Example Give a proof by contradiction of theorem “if 3 n+2 is odd, then n is odd” Proof Let p be “ 3 n+2 is odd“ and q be “n is odd“ We assume that both p and q are true q “n is even“ 3 n+2=3(2 k)+2=6 k+2=2(3 k+2)=2 t even this means p is false ( p is true) But we assume that both p and q are true Then we have a contradiction 3 n+2 is The “if odd (p) and n is even assumption even ( p) conclusion 3 n+2 is odd, then n is odd” is true 136

Exercises pp(85) 1 -3 5 -6 16 -18 137

Proof Methods and Strategy • Exhaustive proof and proof by cases Sometimes we cannot prove a theorem using a single argument that holds for all possible cases. In this situation we consider each case separately. To prove (p 1 p 2 p 3 ……… pn) q The following tautology can be used as a rule of inference: [(p 1 p 2 p 3 … pn) q] [(p 1 q) (p 2 q) (p 3 q) … (pn q)] So we need to prove (p 1 q) (p 2 q) (p 3 q) ……… (pn q) This argument is called a proof by cases Some theorem can be proved by examining a relatively small number of examples, such proof is called exhaustive proof(special type of proof by cases) 138

Proof Methods and Strategy Exhaustive proof (example) • Disproof that (n+1)2 3 n if n is a positive integer with n 4 For n=1 For n=2 For n=3 For n=4 (n+1)2 : (n+1)2 = (1+1)2 = : (n+1)2 = (2+1)2 = : (n+1)2 = (3+1)2 = : (n+1)2 = (4+1)2 = 3 n if n is a positive 22 =4 and 3 n = 31 =3 (T) 32 =9 and 3 n = 32 =9 (T) 42 =16 and 3 n = 33 =27 (F) 52 =25 and 3 n = 34 =81 (F) integer with n 4 is false 139

Proof Methods and Strategy Proof by cases (example) • Proof that if n is an integer, then n 2 n To proof that n 2 n for every integer, we will consider three cases: Case 1: n=0 02=0, we see that 02 0. It follows that n 2 n is true in this case. Case 2: n 1 multiply both sides of the inequality n 1 by n we have n. n 1. n = n 2 n It follows that n 2 n is true in this case. Case 3: n -1 However n 2 0, it implies n 2 n Because the inequality n 2 n holds for all cases, we can conclude that if n is an integer, then n 2 n 140

Proof Methods and Strategy Proof by cases (example) • Prove that the following is true for all real numbers x and y: |xy|= |x| |y| The absolute value function |a| = a if a ≥ 0 =-a if a < 0 Case 1: 2: 3: 4: (both x and y are ≥ 0 ) (x ≥ 0 and y < 0 ) (x < 0 and y ≥ 0 ) (both x and y are < 0 ) 141

Proof Methods and Strategy Proof by cases (example) • Prove that the following is true for all real numbers x and y: max(x, y) = 0. 5 (x + y + |x − y|) The absolute value function is used in this equation, its value depends on whether the number is negative or nonnegative. two cases are considered: Case 1: (x −y < 0) this means (x < y) 0. 5(x + y + |x − y|) = 0. 5(x + y − (x − y)) = 0. 5(x + y − x) = 0. 5(2 y) = y. But if x < y, then we also have max(x, y) = y. Case 2: (x − y ≥ 0 ) this means (x ≥ y) 0. 5(x + y + |x − y|) =0. 5(x + y + (x − y)) =0. 5(x + y + x − y) = 0. 5(2 x) = x. But if x ≥ y, then we also have max(x, y) = x. Thus, in both cases we have 142 max(x, y) = 0. 5 (x + y + |x − y|)

Exercises pp(102 -103) 1 3 -5 143
6059e5f1e5fd89b6f60e5b882023a412.ppt