Кинетика и термодинамика ферментативных реакций Законы классической

Кинетика и термодинамика ферментативных реакций

Законы классической термодинамики в биохимии 1. Основные понятия термодинамики. 2. Первый закон термодинамики. 3. Второй закон термодинамики. 4. Характеристические функции.

Основные понятия термодинамики. • Закрытые системы обмениваются с окружающей средой только энергией, но не массой. Живые организмы представляют собой открытые системы, способные обмениваться с окружающей средой массой и при определенных условиях достигать динамического равновесия (стационарного состояния), но не термодинамического (с максимумом энтропии, см. второй закон термодинамики). • При наличии теплообмена и возможности хотя бы частичной диффузии между телами, составляющими систему, образуется термодинамическая система. • В том случае, когда взаимодействие системы со средой полностью отсутствует, система называется изолированной. • Если состояние термодинамической системы остается неизменным и причиной этого не является какой-либо внешний стационарный процесс, говорят, что система находится в равновесии. Если система состоит из одной фазы, то она гомогенная, в противном случае - гетерогенная.

• Экстенсивные свойства : вес и объем, пропорциональны массе. • Интенсивные свойства: температура, давление, не зависят от массы. • Любое изменение термодинамической системы, приводящее к изменению хотя бы одного термодинамического параметра, называется термодинамическим процессом. • Если единственным результатом обратного процесса в изолированной системе является возвращение системы из конечного состояния в исходное, то такой процесс называют обратимым. • Если в результате прямой или обратной реакции в системе или в ее окружении имеют место длительные изменения, то процесс называют необратимым.

Первый закон термодинамики • Содержание энергии (U) в данной системе увеличивается при совершении работы (А) или передаче тепла (Q): • ΔU = A + Q(1. 1) • В случае цикла, когда ΔU = 0, • A = - Q(1. 2) • Если над системой не совершается никакой работы, т. е. d. U = d. Q, то при равновесном давлении (ΔР = 0) для объема V можно определить новую функцию: • Н = U + PV (1. 3) • где Н - энтальпия (или, менее точно, теплосодержание). U и H - однозначные функции состояния

Закон Гесса Частный случай 1 закона ТД А+В+С=АВС ΔН А+В=АВ ΔН 1 АВ+С=АВС ΔН=ΔН 1+ΔН 2 Тепловой эффект зависит только от начального и конечного состояния веществ и не зависит от промежуточных стадий процесса.

Второй закон термодинамики • Следствием второго закона является увеличение энтропии в природных процессах. Энтропия выражается следующим уравнением: • d. S = d. Q / T(1. 4) Все природные процессы, не противоречащие первому закону термодинамики, можно разделить на две группы: • самопроизвольные при данных условиях; • Несамопроизвольные Работа не может быть выполнена исключительно за счет тепловой энергии окружающей среды

Статистическая формулировка закона • Число микросостояний, посредством которых может быть достигнуто данное макросостояние, называется термодинамической вероятностью. • Статистический анализ показывает, что самопроизвольные процессы сопровождаются увеличением термодинамической вероятности. Т. е. , процессы, протекающие в изолированной системе, сопровождаются увеличением энтропии.

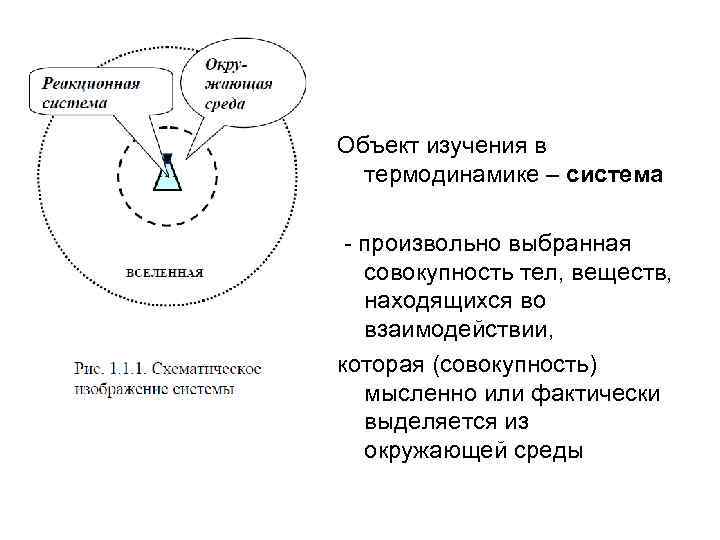Объект изучения в термодинамике – система - произвольно выбранная совокупность тел, веществ, находящихся во взаимодействии, которая (совокупность) мысленно или фактически выделяется из окружающей среды

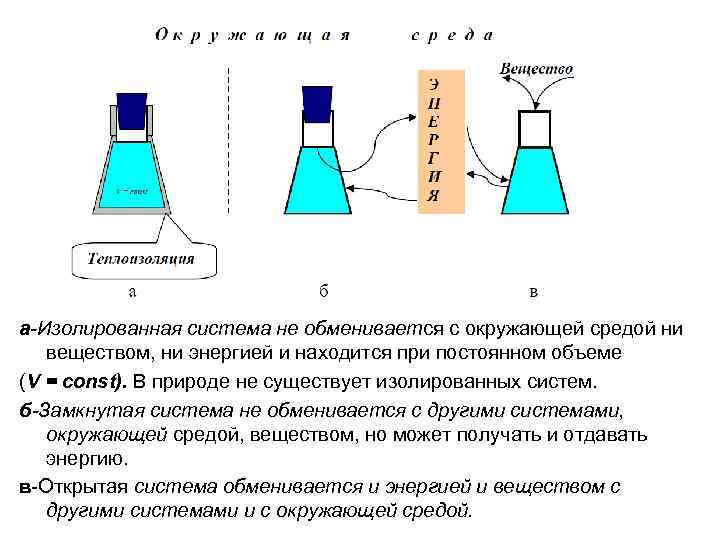а-Изолированная система не обменивается с окружающей средой ни веществом, ни энергией и находится при постоянном объеме (V = const). В природе не существует изолированных систем. б-Замкнутая система не обменивается с другими системами, окружающей средой, веществом, но может получать и отдавать энергию. в-Открытая система обменивается и энергией и веществом с другими системами и с окружающей средой.

Внутренняя энергия U Каждое тело, вещество, система имеет определенное значение этого запаса внутренней энергии U. В понятие внутренней энергии системы не входит потенциальная энергия положения системы в пространстве и кинетическая энергия движения всей этой системы как целого. То есть внутренняя энергия какой-либо системы, везде одна и та же. 1 кал = 4. 184 Дж

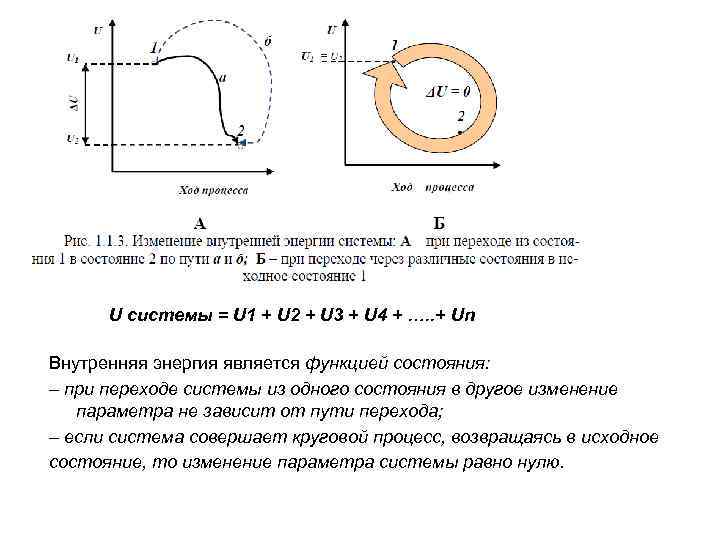U системы = U 1 + U 2 + U 3 + U 4 + …. . + Un Внутренняя энергия является функцией состояния: – при переходе системы из одного состояния в другое изменение параметра не зависит от пути перехода; – если система совершает круговой процесс, возвращаясь в исходное состояние, то изменение параметра системы равно нулю.

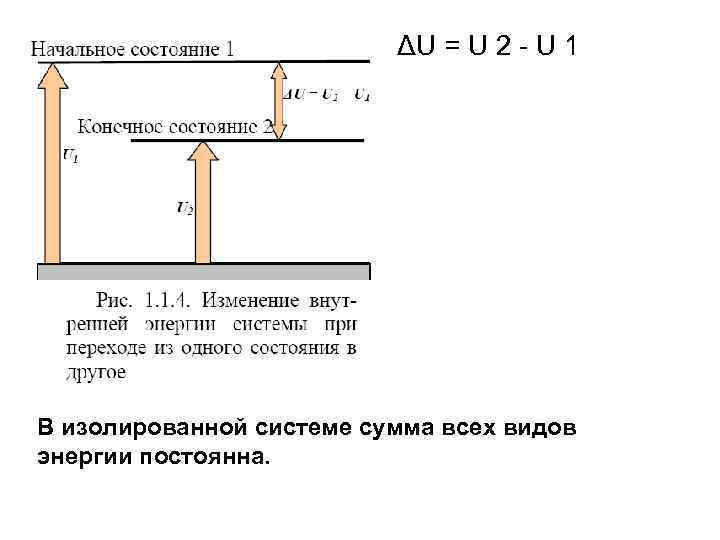ΔU = U 2 - U 1 В изолированной системе сумма всех видов энергии постоянна.

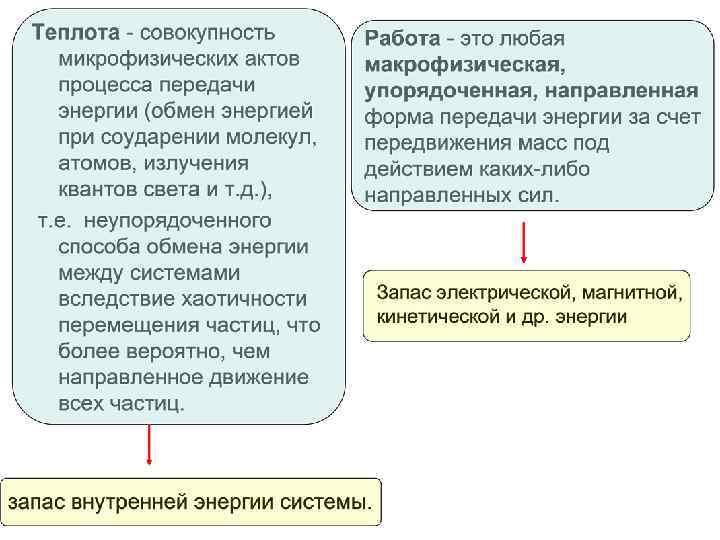
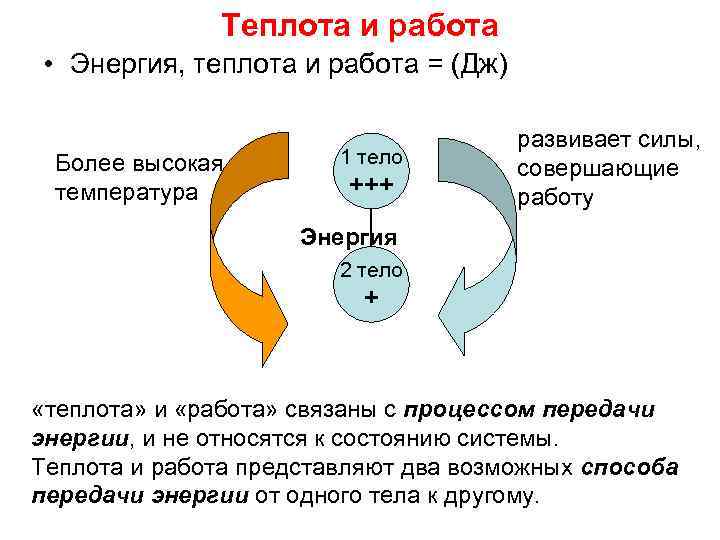Теплота и работа • Энергия, теплота и работа = (Дж) Более высокая температура 1 тело +++ развивает силы, совершающие работу Энергия 2 тело + «теплота» и «работа» связаны с процессом передачи энергии, и не относятся к состоянию системы. Теплота и работа представляют два возможных способа передачи энергии от одного тела к другому.

Характеристические функции • • • изохорно-изотермический потенциал; изобарно-изотермический потенциал; внутренняя энергия; энтальпия; энтропия. Потенциал - функция, изменение которой однозначно связано с работой. Эта функция имеет размерность энергии (как и работа).

Внутренняя энергия - запас энергии системы при постоянном объеме и энтропии. Δ U = T ΔS - P ΔV (1. 5) Энтальпия -общий запас энергии системы при постоянном давлении и энтропии. Δ H = T ΔS + V ΔP(1. 6) Энтропия - мера беспорядка, величина, с помощью которой при постоянной температуре можно получить какое-либо количество теплоты Δ S = ΔQ / T (1. 7) Энергия Гельмгольца - свободная энергия, идущая на совершение полезной работы при постоянном объеме и температуре (изохорно-изотермический потенциал). F = U - TS Δ F = -P ΔV - S ΔT(1. 8)

Энергия Гиббса - свободная энергия, идущая на совершение полезной работы при постоянном давлении и температуре (изобарно-изотермический потенциал). G = H - TS d. G = - Sd. T + Vd. P (1. 9) Для однокомпонентной гомогенной системы свободная энергия одного моля вещества (молярная свободная энергия) является химическим потенциалом: μ= (d. G /dn)P, T = (d. F /dn)V, T = (d. U /dn)V, S = (d. H /dn) P, S (1. 10) где n - число молей вещества. Для многокомпонентной системы химический потенциал i-го компонента определяется как μi = (d. G /dni) P, T, nj (1. 11) Где j = 1, . . . k , j <> i. Изменение свободной энергии в системе может быть представлено в виде суммы произведений химических потенциалов составляющих ее компонентов на изменение числа их молей: (1. 12) В состоянии равновесия химические потенциалы компонентов данной системы равны.