f4b0242ef9337e88a7984cf3afc726e7.ppt
- Количество слайдов: 56

Kinetic Algorithms Data Structure for Mobile Data

Plan Motivation n Introduction n Illustrative example n Applications n 2 -D Convex Hull n Closest pair in 2 -D n n Others Issues

Motivation Maintain an attribute of interest in a system of geometric objects undergoing continuous motion. n Take advantage of the coherence present in continuous motion to process a minimal number of combinatorial event. n

Introduction n Problems such as convex hull and closest pair maintenance have been extensively studied: Static objects n Insertion and deletion operations n n Wasteful of computation n Compute form scratch

Introduction KDS? n KDS: Kinetic Data Structure n n Process of discrete events associated with continuously changing data. Kinetisation n Process of transforming an algorithm on static data into a data structure which is valid for continuously changing data.

Introduction The Big Picture Resemble to a sweep-line/plane algorithm n Use of a global event queue as interface between KDS and object in motion. n Sweep line Time

Introduction Flight plan n Use of flight plans The motion of the objects is known in advance n BUT: n • Can be imprecise (use of intervals) • Can be updated
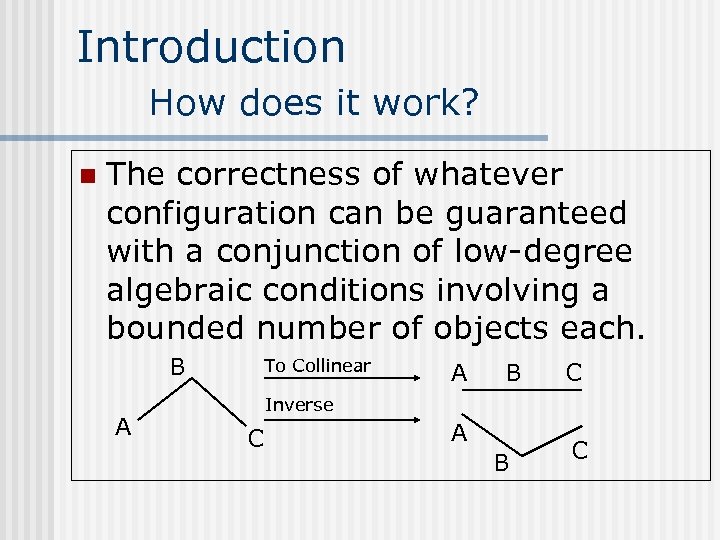
Introduction How does it work? n The correctness of whatever configuration can be guaranteed with a conjunction of low-degree algebraic conditions involving a bounded number of objects each. B A To Collinear A B C Inverse C A B C

Introduction Certificates n A certificates will guarantee the correctness of any configurations

Introduction Timeline n n Event queue contains KDS events corresponding to times (precise / interval) when certificates might change sign. IF ( flight plan of O updated ) THEN All the certificates involving O must be recalculated and updated.
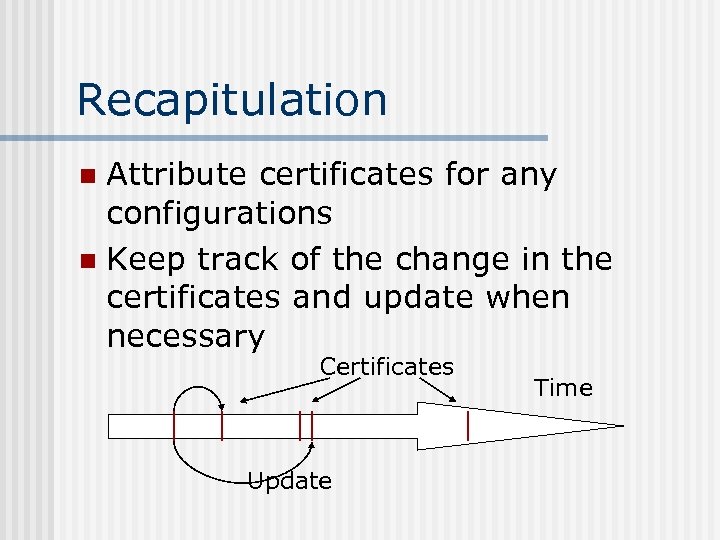
Recapitulation Attribute certificates for any configurations n Keep track of the change in the certificates and update when necessary n Certificates Update Time

Definitions n Certificates n n Complexity n n Guarantee the correctness Number system. of points moving in a Small cost n If it running time of the order or

Definitions n Internal events (IE) n n Events process by the structure for its internal needs External events (EE) Events affecting the configuration we are maintaining. n Lower bound for IE n

Definitions n Efficiency n n n Responsiveness n n If the ratio IE / EE is small. Range: 1 to Infinity Worst-case cost of processing a certificate Size n Maximum number of events it needs to schedule in the event queue

Definitions n Compact n n If size linear to the number of moving objects Local n If the maximum number of events in the event queue that depend on a single object is small

Illustrative example n Y Consider the following 1 D situation n Given a set of n points moving continuously along the y-axis, we are interested to know which is the topmost point. • Constant speed • Arbitrary initial configuration

Solution 1 Trivial Case Draw the lines in the ty-plane n Compute the upper envelope of the set of lines. n Efficient algorithm but does not support update of the flight plan. n

Solution 2 Schedule-Deschedule n n Maintain, on-line, the sorted order along the y-axis Schedule event that is the first time when two consecutive points cross. n n n Destroy and create 2 adjacencies Schedule and deschedule up to 2 new events Not efficient: process up to events.
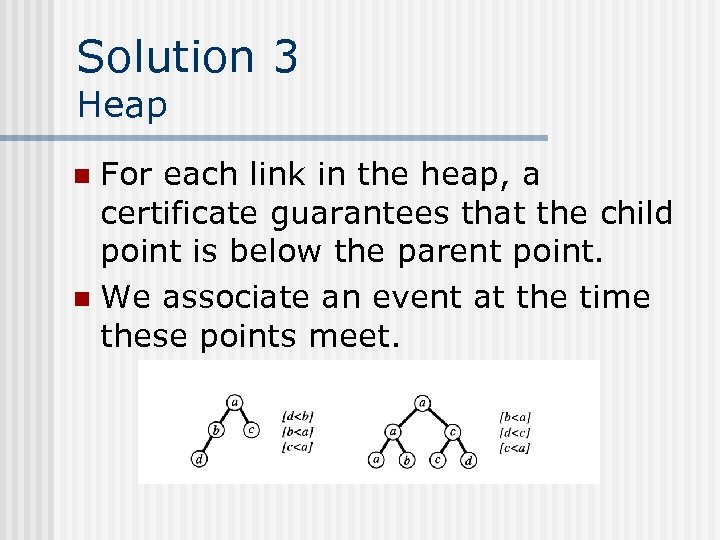
Solution 3 Heap For each link in the heap, a certificate guarantees that the child point is below the parent point. n We associate an event at the time these points meet. n
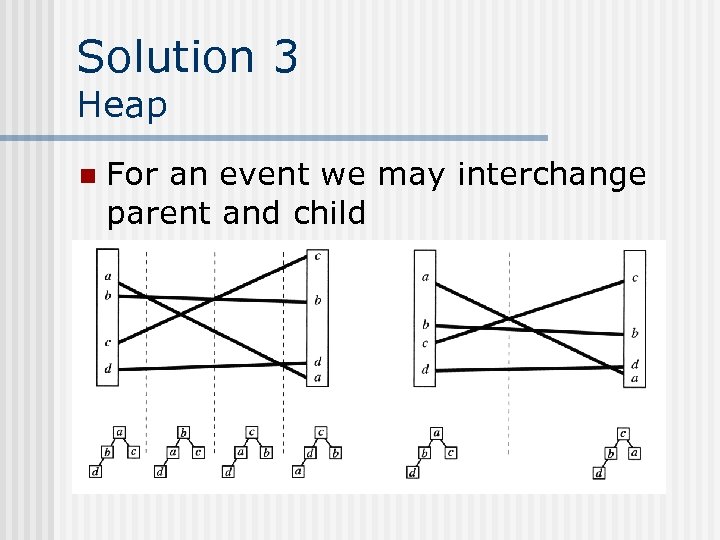
Solution 3 Heap n For an event we may interchange parent and child

Solution 4 Kinetic Tournament Consider a divide-and-conquer algorithm, like a tournament from bottom to up for computing a global leader. comparisons n As long as each of the comparison remain valid the identity of the maximum remains valid. n

Solution 4 Kinetic Tournament Imagine that a particular comparison involved flip and precolated up the tree. n For a balanced tree the computation is made in time and can affect at most certificates. n

Solution 4 Kinetic Tournament n For points with constant speed, similar to the computation of the upper-envelope in the ty-plane. n In the worst case we have new leaders, each computed in time, for a total worst case running time of
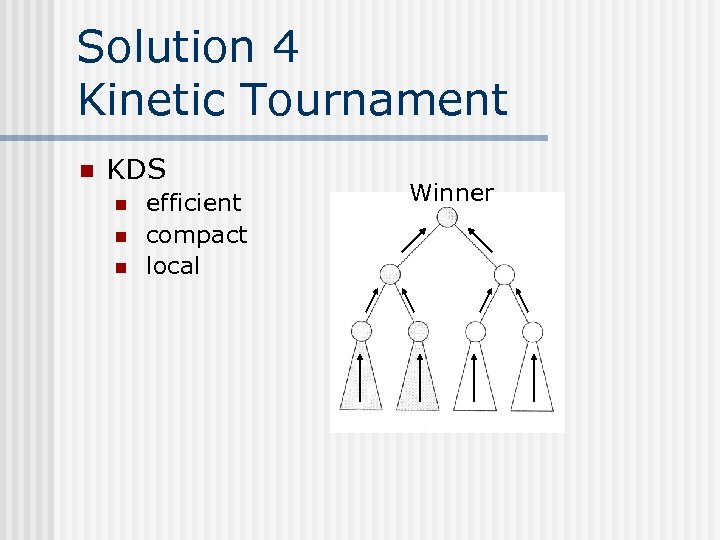
Solution 4 Kinetic Tournament n KDS n n n efficient compact local Winner

2 D Convex Hull n Problem n n Maintain the convex hull of a set of moving points in 2 D. Dual form n Point (p, q) to the line y=px+q

2 D Convex Hull n Goal: Maintain the upper envelope of the set of lines

2 D Convex Hull n n Perform a kinetic tournament. From a red and a blue chain maintain the purple upper envelope of the 2 chains

2 D Convex Hull Kinetisation We keep a record of the entire computation in a balanced binary tree n Each node is in charge of maintaining the upper envelope of two upper envelopes computed by its children n If a event creates a change, the event is process through the tree. n

2 D Convex Hull Operators <x n <y n <s n X value comparison Y value comparison Slope comparison Ce(ab) Contender edge n Color of the vertex n

2 D Convex Hull Certificates

2 -D Convex Hull Certificates
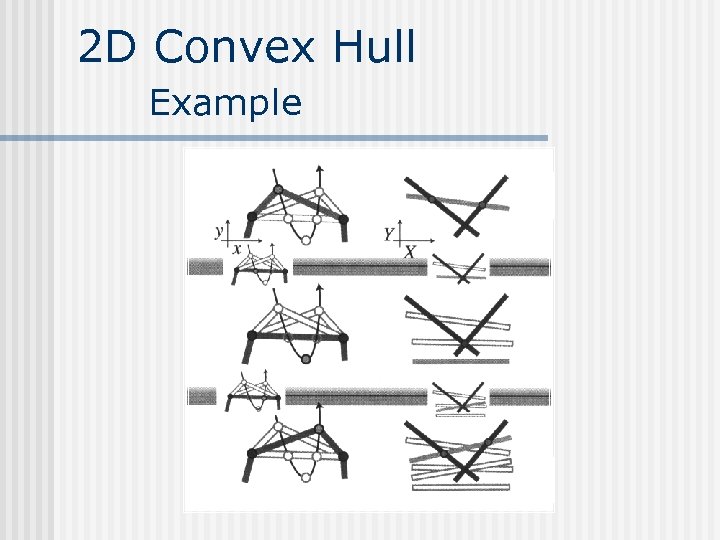
2 D Convex Hull Example

2 -D Convex Hull n Lemma 2. 1 Consider a configuration C of two convex piecewise linear functions and the certificate list L for their upper envelope as defined earlier. Let C’ be a configuration for which all the certificates of L hold. Then the upper envelope of C’ has the same combinatorial description as that of C.

2 D Convex Hull Proof The x-certificates prove the correctness of the contender edge pointer. n Any vertex that has a y-certificate in L is also guaranteed to be placed in C’ and in C. n

2 D Convex Hull Proof n We can show that the vertices without y-certificates can not be placed differently in C and C’

2 D Convex Hull n Certificate updates n Lemma 2. 2 n The following procedure correctly updates the certificate list when the configuration events happen

2 D Convex Hull Analysis n Theorem 2. 3 • The KDS for maintaining the convex hull is efficient, responsive, compact and local n Proof • Responsive: • Compact : • Local: • Efficient: in the worst case

2 D Convex Hull Demo n Demo

Closest Pair in 2 D Problem definition n Given a set S of n moving points find the two closest points in S. n Traditional static algorithms are illadapted for the kinematisation.

Closest Pair in 2 D Static Algorithm We divide the space around each vertex into six 60º wedges, the nearest neighbor of each point is the closest of the nearest neighbor in the six wedges. n ADD PICTURE n

Closest Pair in 2 D Definitions Dom(p): The right extending wedge that make ± 30º angles with the x axis. n Circ(p, r): The circle of radius r centered at p. n We denote the closest pair in S, (a, b) n

Closest Pair in 2 D Problem definition n Lemma 3. 1 n n Point b is not contained in Dom(p) for any third point p with a to the left of b. Lemma 3. 2 n The leftmost point in Dom(a) is b.
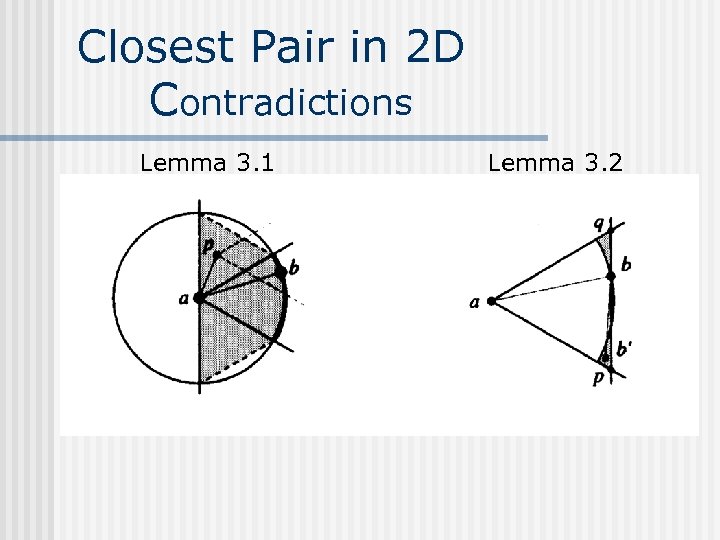
Closest Pair in 2 D Contradictions Lemma 3. 1 Lemma 3. 2
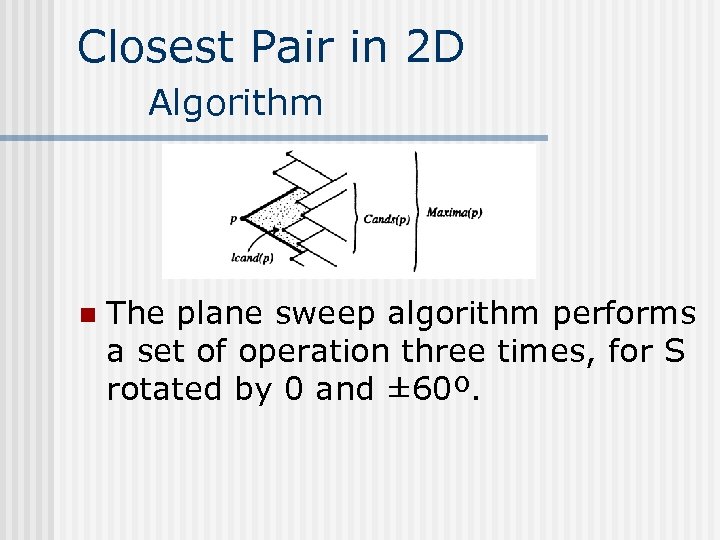
Closest Pair in 2 D Algorithm n The plane sweep algorithm performs a set of operation three times, for S rotated by 0 and ± 60º.

Closest Pair in 2 D Algorithm n For each point p in S from right to left Set Cands(p) = Maxima Dom(p) n Set lcand(p) to be the leftmost element of cands(p) n Delete points of Cands(p) from Maxima n Insert p into Maxima at its proper place in y-order n n Repeat for the three directions

Closest Pair in 2 D Algorithm n Analysis Sorting: n Compute Cands(p): n Finding lcand(p): in the worst case n Splitting and inserting: n n Total:

Closest Pair in 2 D Kinetisation n Certificates The projection of the point on x for S rotated by 0 and ± 60º. n Each point belong to a maximum of six certificates, involving is two neighbors in each of the three sorted order. n
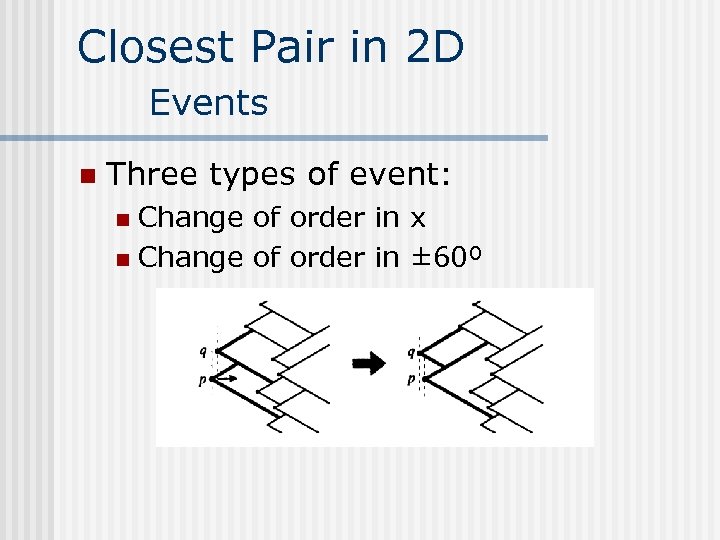
Closest Pair in 2 D Events n Three types of event: Change of order in x n Change of order in ± 60º n

Closest Pair in 2 D Updates

Closest Pair in 2 D Updates

Closest Pair in 2 D Analysis n The KDS for the closest pair problem is efficient, responsive, compact and local. n Efficient: The number of events process by the KDS is a logarithmic factor more then the maximum number of external events.

Closest Pair in 2 D Analysis n Compact: • There is events in the queue at any time, for the certificates and for the kinetic tournament. n Local: • Each point belongs to ar most six certificates and to at most three pair and in pair participate to at most events in the kinetic tournament

Closest Pair in 2 D Demo n Demo
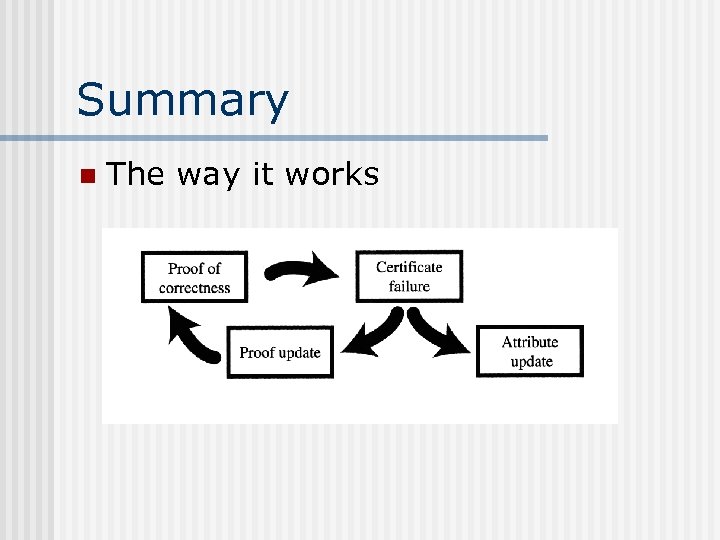
Summary n The way it works

Further Issues Avoid the problem related to the finite precision arithmetic. (sequencing of the events) n Change the definition of efficiency to make it proportional to the number if external events n Adapt the algorithm to real time computation n

References J. Basch and J. Guilbas. Data Structures for Mobile Data. J. of Algorithms 31, 1 -28 (1999). n J. Basch and al. Data Structures for Mobile Data. SODA 1997, 756 -767. n http: //graphics. stanford. edu n
f4b0242ef9337e88a7984cf3afc726e7.ppt