Kinetic Algorithms Approximation and Trade-offs Pankaj K Agarwal

Kinetic Algorithms: Approximation and Trade-offs Pankaj K. Agarwal Duke University

Motivation Applications • Location based services • Animation • Physical simulation • Mobile and wireless networks Need algorithms and data structures for processing, analyzing, querying moving objects Dynamic data structures not suitable for handling moving objects

Modeling Motion p(t) = (x(t), y(t)): Position of p at time t Øx(t), y(t): polynomials ØDegree of motion: max degree of x(), y() ØLinear motion: Degree = 1 • p(t) = a t + b, a, b in R 2 ØMostly assume motion to be linear ØTrajectory of points can change ØTrajectory can be piecewise linear

Early Work ØOff-line setting: Entire motion known in advance ØBound the # combinatorial/topological changes in geometric attributes under algebraic motion [Atallah 1985] • Convex hull, closest pair, Voronoi diagram # combinatorial changes in • Convex hull: ≈n 2 • closest pair: Q(n 2)

Early Work: Open Problems Ø# edge-flips in Delaunay triangulation of a point set, each point moving with fixed velocity • Upper Bound O(n 3) • Lower Bound W(n 2) Ø# changes in the smallest disk containing points • Smallest disk is defined by 2 or 3 points lying on its boundary

Kinetic Data Structures [Basch, Guibas, Hershberger 1999] ØEvent based framework ØStore some auxiliary information to expedite the simulation external event internal event • A

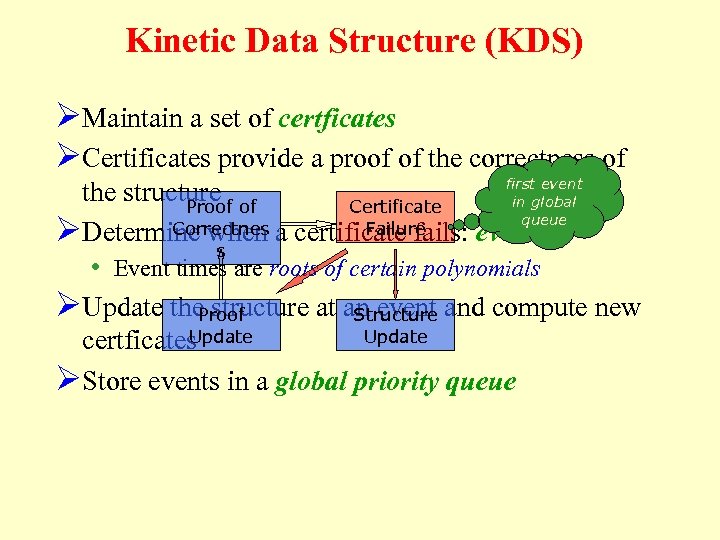Kinetic Data Structure (KDS) ØMaintain a set of certficates ØCertificates provide a proof of the correctness of first event the structure of in global Proof Certificate queue Correctnes a certificate fails: event Failure ØDetermine when s • Event times are roots of certain polynomials ØUpdate the. Proof structure at an event and compute new Structure Update certficates ØStore events in a global priority queue

Kinetic Data Structures (KDS) Performance of KDS measured as Ø# events (efficiency) Ø# certificates (compactness) ØTime spent at each event (locality) Efficient KDS developed for many problems [A. et al. 2001][Guibas 2004] Issues Ø Too many events for many KDS Ø Computing event times is expensive Ø Querying moving objects • No need to maintain the structure at all times

Trade Offs in KDS ØEfficiency vs Approximation ØEfficiency vs Accuracy ØQuerying Moving Objects • Range searching, nearest-neighbor searching on moving points • No need to maintain the structure at all times

I. Efficiency vs Approximation

KDS using Coresets S: Set of n moving points in R 2 Maintain the diameter (width, smallest enclosing box) of S Ø [A. , Guibas, Hershberger, Veach] • Diametral pair can change Q(n 2) times • KDS with ~ n 2 events ØCan we maintain the approximate diameter of S more efficiently? • Is there a small subset Q of S s. t. for all t diam(Q(t)) ≥ (1 -e) diam(S(t)) ØQ: coreset of S

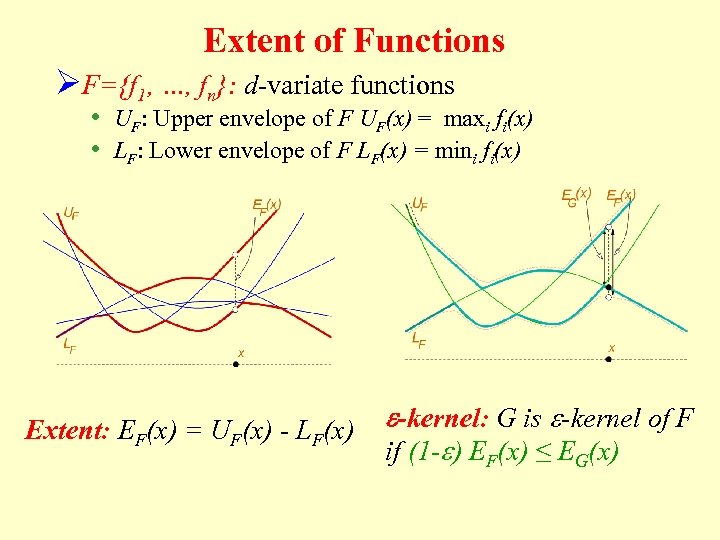Extent of Functions ØF={f 1, …, fn}: d-variate functions • UF: Upper envelope of F UF(x) = maxi fi(x) • LF: Lower envelope of F LF(x) = mini fi(x) Extent: EF(x) = UF(x) - LF(x) e-kernel: G is e-kernel of F if (1 -e) EF(x) ≤ EG(x)

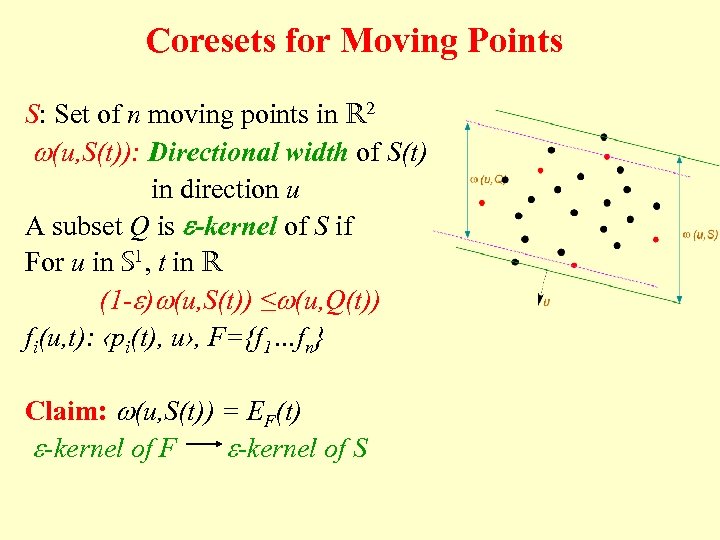Coresets for Moving Points S: Set of n moving points in R 2 w(u, S(t)): Directional width of S(t) in direction u A subset Q is e-kernel of S if For u in S 1, t in R (1 -e)w(u, S(t)) ≤w(u, Q(t)) fi(u, t): ‹pi(t), u›, F={f 1…fn} Claim: w(u, S(t)) = EF(t) e-kernel of F e-kernel of S

Kernels of Moving Points Theorem [A. , Har-Peled, Varadarajan] F={f 1, …, fn}: d-variate polynomials of fixed degree; e > 0 parameter An e-kernel of F of size 1/e. O(1) can be computed in time O(n+ 1/e. O(1)). Corollary: S: n points moving with fixed velocity in 2 D, e > 0 parameter. An e-kernel of S of size O(1/e 3/2) can be computed in time O(n+ 1/e 3).

Maintaining a Bounding Box Maintain an e-approximation of the bounding box of S Ø Compute an e-kernel Q of S Ø Smallest Bounding box defined by: left-, right, top, and bottom-most points Ø Use KDS to maintain these 4 points of Q Ø Events: When one of them changes Same approach works for maintaining width, diameter, … approximately

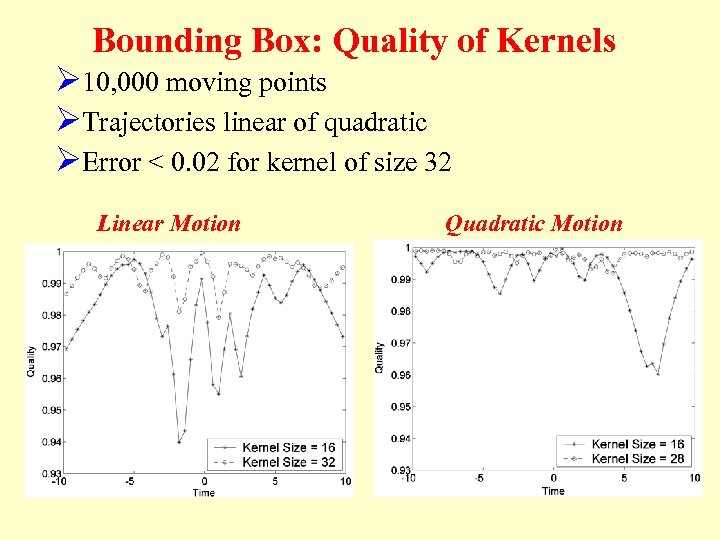Bounding Box: Quality of Kernels Ø 10, 000 moving points ØTrajectories linear of quadratic ØError < 0. 02 for kernel of size 32 Linear Motion Quadratic Motion

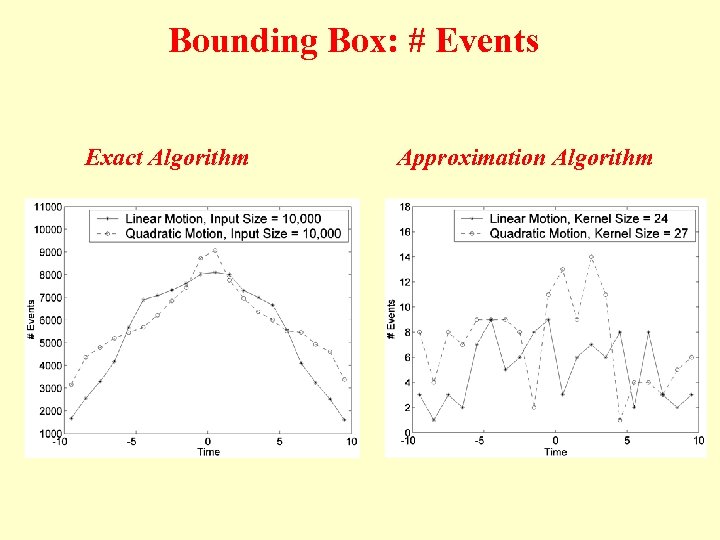Bounding Box: # Events Exact Algorithm Approximation Algorithm

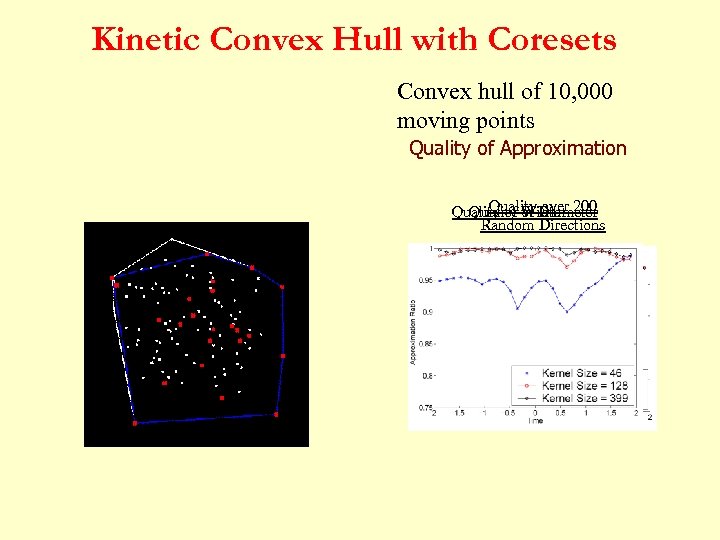Kinetic Convex Hull with Coresets Convex hull of 10, 000 moving points Quality of Approximation Quality over Quality of Diameter Quality of Width 200 Random Directions

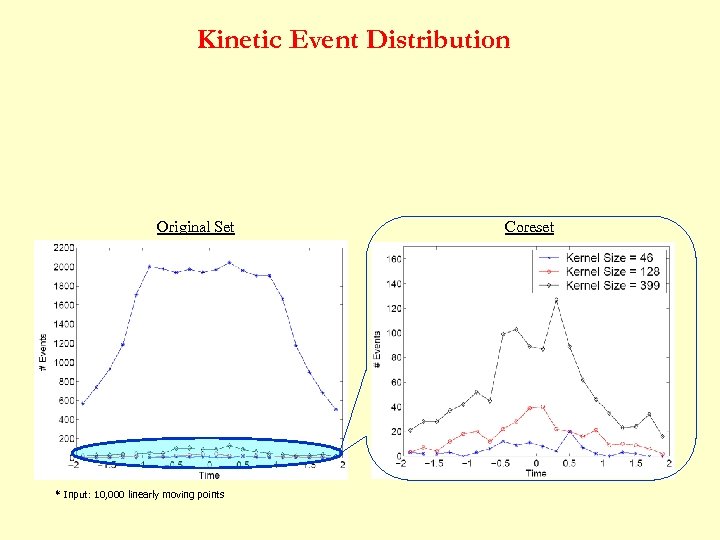Kinetic Event Distribution Original Set * Input: 10, 000 linearly moving points Coreset

Kinetic Triangulations ØDelaunay triangulation in R 2 • O(n 3) edge flips ØAn arbitrary triangulation in R 2 • ≈n 2 edge flips [A. , Wang, Yu 2004] Can we maintain an almost Delaunay triangulation with ≈n 2 edge flips? [A. , Guibas, Gao, Koltun, Sharir 2006] Maintain a subgraph of Delaunay triangulation that • contains W(n) Delauanay edges • contains all wide Delaunay edges • performs ≈ n 2 edge flips Is there a good definition of almost Delaunay triangulation?

Efficiency vs Accuracy Robust KDS

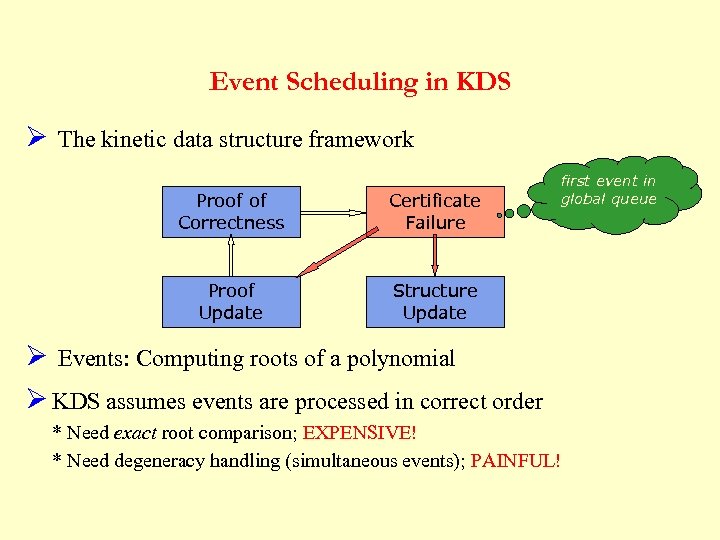Event Scheduling in KDS Ø The kinetic data structure framework Proof of Correctness Certificate Failure Proof Update first event in global queue Structure Update Ø Events: Computing roots of a polynomial Ø KDS assumes events are processed in correct order * Need exact root comparison; EXPENSIVE! * Need degeneracy handling (simultaneous events); PAINFUL!

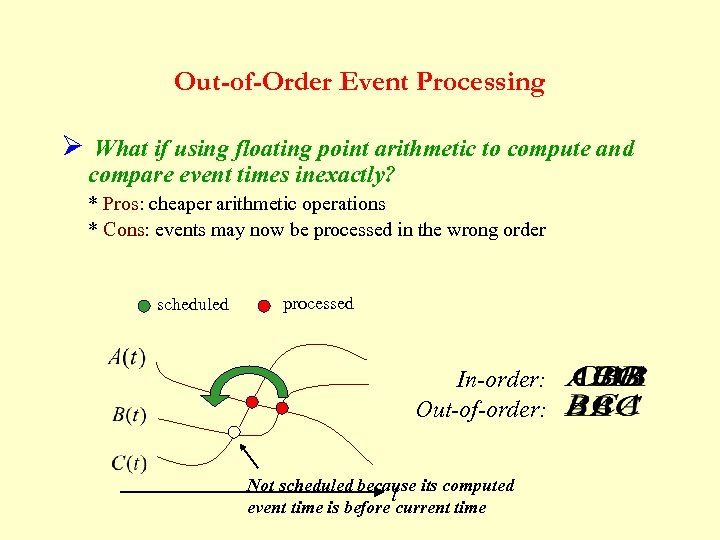Out-of-Order Event Processing Ø What if using floating point arithmetic to compute and compare event times inexactly? * Pros: cheaper arithmetic operations * Cons: events may now be processed in the wrong order scheduled processed In-order: Out-of-order: Not scheduled because its computed t event time is before current time

Out-of-Order Event Processing ØIssues in out-of-order event processing * Does the KDS fall into an infinite loop? * Can an event be delayed for too long? * Can error in the maintained structure be too large? [Abam, A. , de Berg, Yu, 2006] ØRobust KDS to address these issues • KDS is correct at all times except near the event times • No event is delayed too long • Bonus: Degeneracies are handled automatically

Model of Robust KDS Ø Root computation procedure CROP * : input polynomial; : error bound in CROP * CROP( ) does the following (1) find set of disjoint, open event intervals s. t. each and they cover all roots (2) find parity of the number of roots lying in each (3) return intervals with odd number of roots

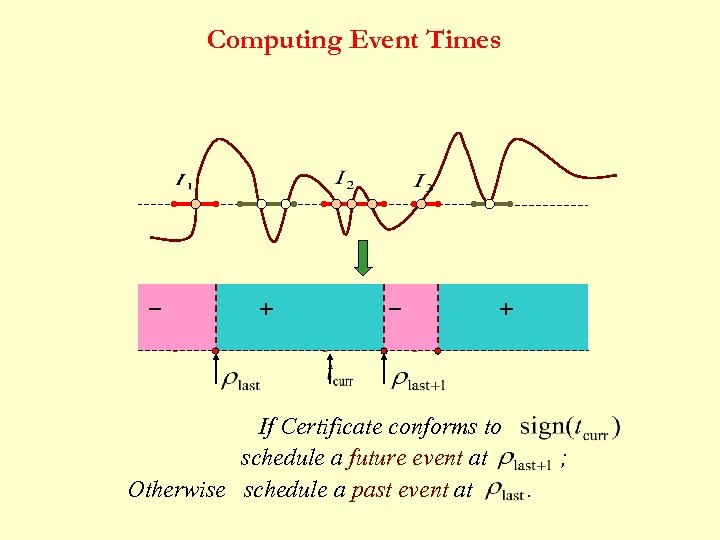Computing Event Times _ + If Certificate conforms to schedule a future event at Otherwise schedule a past event at ; .

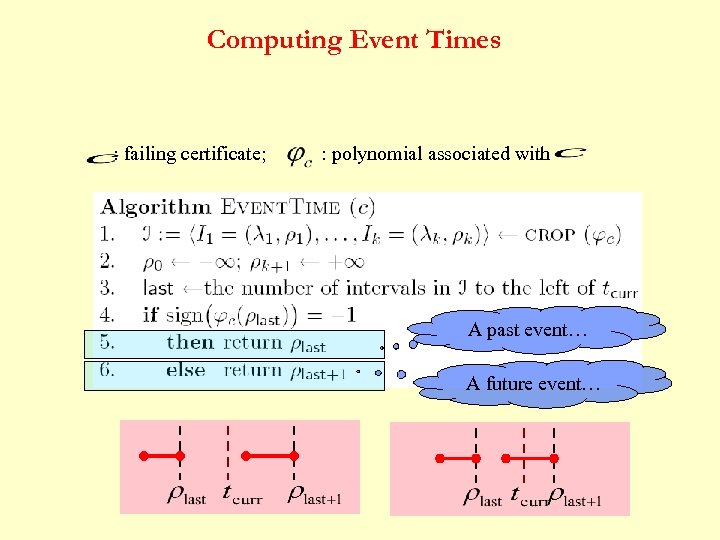Computing Event Times : failing certificate; : polynomial associated with A past event… A future event…

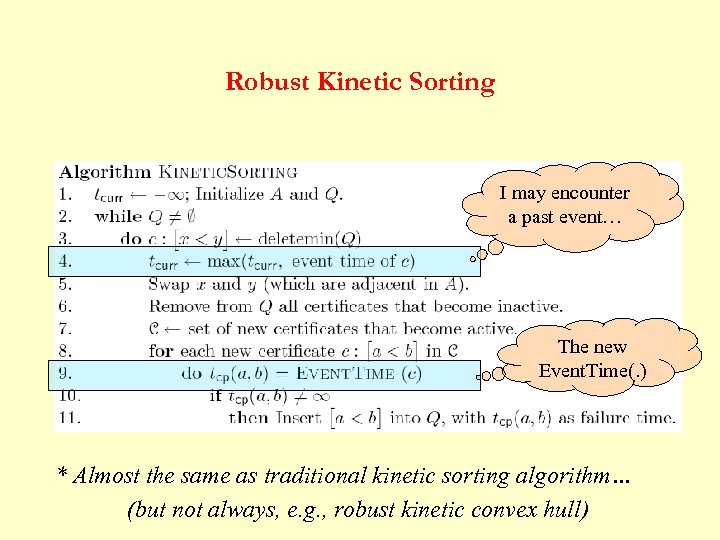Robust Kinetic Sorting I may encounter a past event… The new Event. Time(. ) * Almost the same as traditional kinetic sorting algorithm… (but not always, e. g. , robust kinetic convex hull)

Nice Properties Ø The KDS does not fall into an infinite loop Ø List is correct except within -neighborhood of actual event times

Nice Properties Ø Events may be delayed by at most time long Ø Even when list is incorrect, it is still close to true sorted list geometrically : i-th pt in maintained list : i-th pt in sorted list : maximum velocity over time interval

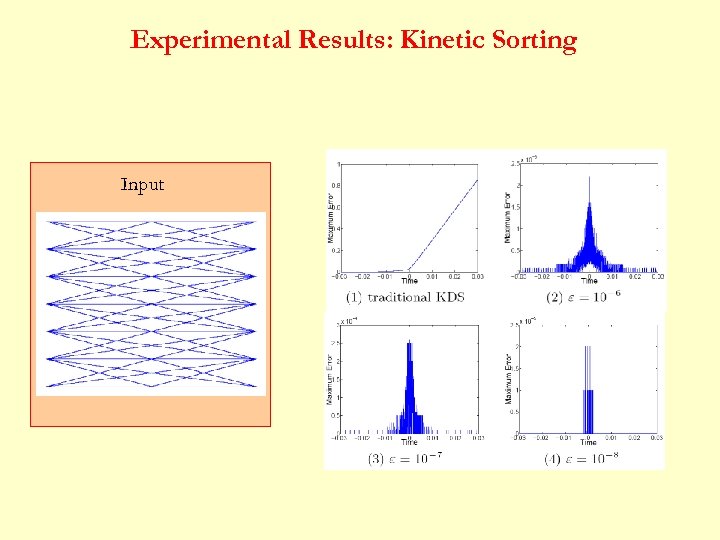Experimental Results: Kinetic Sorting Input

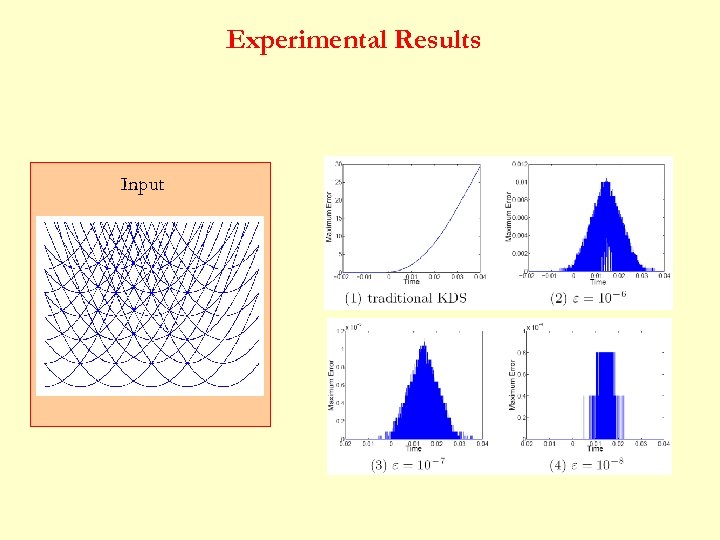Experimental Results Input

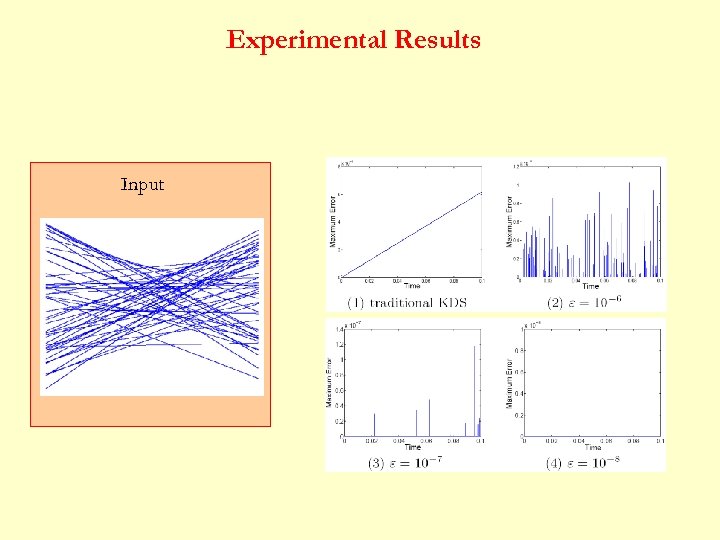Experimental Results Input

Other Robust KDS [Abam, A. , de Berg, Yu, 2006] ØKinetic tournament ØConvex hull, kd-tree, range-tree, … ØIs there a robust KDS for Delaunay triangulation? • Find a sequence of edge-flips to convert a selfintersecting triangulation to Delaunay triangulation

Soft KDS [Czumaj, Sohler 2005] ØApproximate KDS ØRepair the structure only when necessary ØUse the ideas from property testing to ensure KDS is almost correct with high probability ØCompetitive analysis to measure the performance of KDS

III. Querying Moving Objects

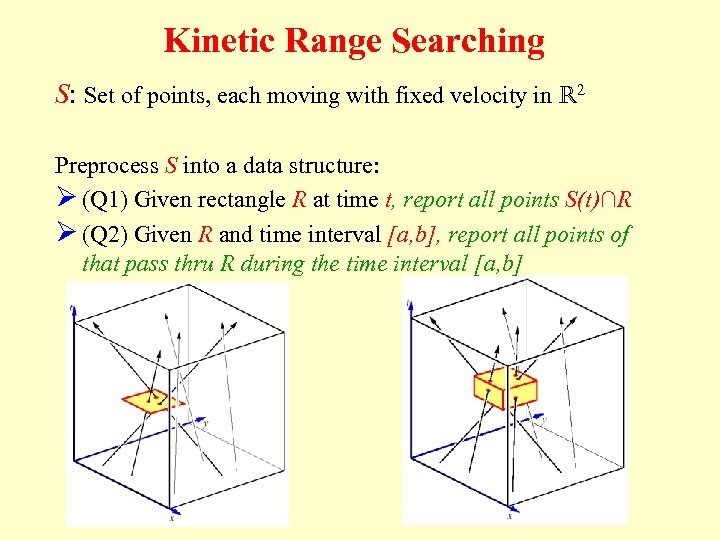Kinetic Range Searching S: Set of points, each moving with fixed velocity in R 2 Preprocess S into a data structure: Ø (Q 1) Given rectangle R at time t, report all points S(t)∩R Ø (Q 2) Given R and time interval [a, b], report all points of that pass thru R during the time interval [a, b]

KDS Approach ØKientic range trees [A. , Arge, Erickson 2003] • • O(n log n) space, O(log n + k) query (Q 1) Use KDS approach to update range tree Q(n 2) events; O(log 2 n) (amortized) time at each event Queries have to arrive in chronological order ØKinetic kd-trees [A. Gao, Guibas 2003] • O(n) space, O(n 1/2 + k) query (Q 1) • Q(n 2) events; O(log 2 n) (amortized) time at each event • Queries have to arrive in chronological order ØWhat if queries do not arrive in chronological order? Why spend time processing events?

Kinetic Range Searching Partition tree based approach [A. , Arge, Erickson] ØO(n) space, O(n 1/2 + k) query time ØO(log 2 n) insertion/deletion of a point Answering (Q 1) query A similar approach works for (Q 2) queries

Time-Responsive Indexing Ø Time-responsiveness * Near future queries need to be answered more quickly * Optimize structure for near future * Approximate distant future Ø Results [A. , Arge, Erickson, Yu, 2004] * Orthogonal range queries in R 1 , R 2 ~n space, (f(tq)/n)1/2 + log. O(1) n + k query time f(tq): # events between current time and tq (near future) (distant future)

Example: 1 D Time-Responsive Indexing Ø : set of linearly moving points in R 1 * Given interval and time , report Ø In tx-plane, reduces to stabbing query * Report all lines intersecting a vertical segment Ø Overall structure * Divide tx-plane into slabs * i-th slab contains events (vertices) * A window structure for each slab to answer stabbing query

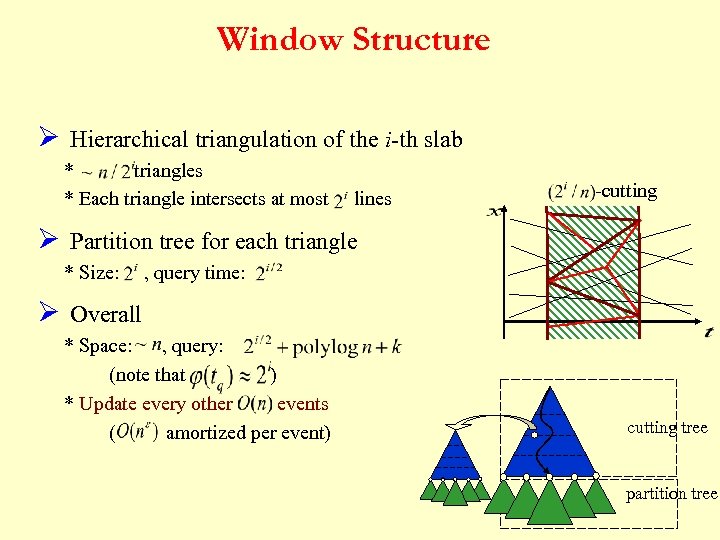Window Structure Ø Hierarchical triangulation of the i-th slab * triangles * Each triangle intersects at most lines -cutting Ø Partition tree for each triangle * Size: , query time: Ø Overall * Space: , query: (note that ) * Update every other events ( amortized per event) cutting tree partition tree

References [Abam, Agarwal, de Berg, Yu, 2006] Out-of-order event processing in kinetic data structures. ESA’ 06. [Abam, de Berg, 2005] Kinetic sorting and kinetic convex hulls. So. CG’ 05. [Agarwal, Arge, Erickson, 2003] Indexing moving points. J. Comput. Syst. Sci. , 66(1). [Agarwal, Arge, Erickson, Yu, 2004] Efficient tradeoff schemes in data structures for querying moving objects. ESA’ 04. [Agarwal, Arge, Vahrenhold, 2001] Time responsive external data structures for moving points. WADS’ 01. [Agarwal, Gao, Guibas, Koltun, Sharir, 2006] Stable Delaunay triabgulation, manuscript. [Agarwal, Har-Peled, Varadarajan, 2004] Approximating extent measures of points. J. ACM, 51(4). [Agarwal, Wang, Yu] Kinetic triangulation, SOCG’ 04. [Czumaz, Sohler, 2005] Soft kinetic data structures, SODA. [Guibas 2004] Kinetic data structures, Handbook of DCG, 2 nd edition, [Yu, Agarwal, Poreddy, Varadarajan, 2004] Practical methods for shape fitting and kinetic data structures using coresets. So. CG’ 04.

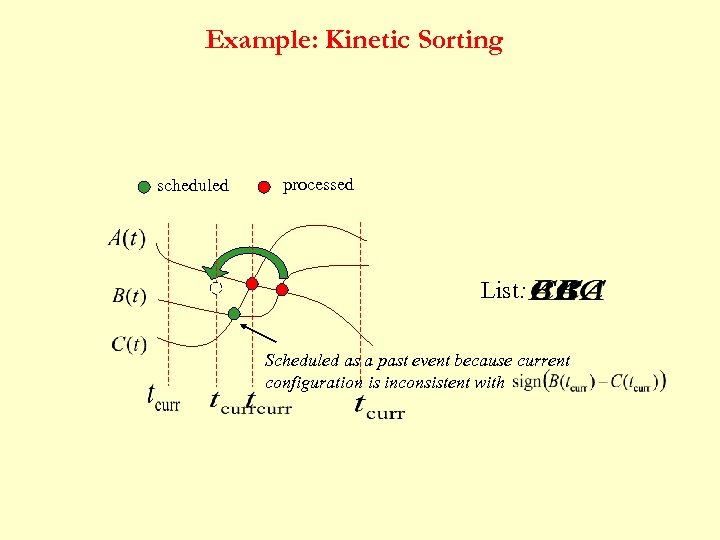Example: Kinetic Sorting scheduled processed List: Scheduled as a past event because current configuration is inconsistent with