Кинематика жидкости Изучает

Кинематика жидкости Изучает геометрические свойства движения жидкости

Описание движения жидкости методами Лагранжа и Эйлера Лагранжево описание – описание движения любой фиксированной частицы жидкости При t=t 0 координата частицы жидкости x 0 , y 0, z 0 Все кинематические характеристики – функции времени и начальных координат частицы

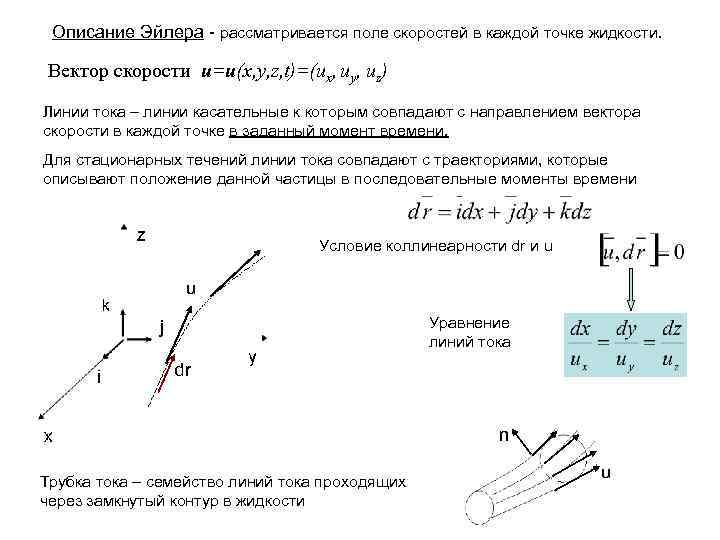Описание Эйлера - рассматривается поле скоростей в каждой точке жидкости. Вектор скорости u=u(x, y, z, t)=(ux, uy, uz) Линии тока – линии касательные к которым совпадают с направлением вектора скорости в каждой точке в заданный момент времени. Для стационарных течений линии тока совпадают с траекториями, которые описывают положение данной частицы в последовательные моменты времени Условие коллинеарности dr и u Уравнение линий тока dr n u Трубка тока – семейство линий тока проходящих через замкнутый контур в жидкости

Классификация потоков жидкости. По геометрическому признаку потоки подразделяются: 1. Пространственные (трехмерные) 2. Плоские ( двумерные) 3. осесимметричные 4. одномерные По временному признаку: 1. стационарные (установившиеся); 2. нестационарные;

1. Расход жидкости через поверхность S u n S u 2. Дивергенция скорости – (расходимость скорости) 3. Циркуляция скорости u dl

4. Вихрь скорости =rotu и угловая скорость вращения частицы жидкости y u r θ=ωt t z x water Ротор ( вихрь) скорости = удвоенной скорости вращения жидкой частицы

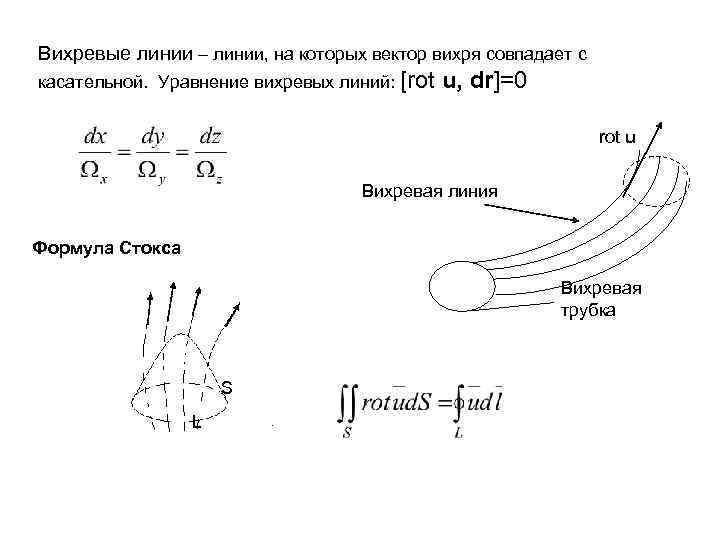Вихревые линии – линии, на которых вектор вихря совпадает с касательной. Уравнение вихревых линий: [rot u, dr]=0 rot u Вихревая линия Формула Стокса Вихревая трубка S L L

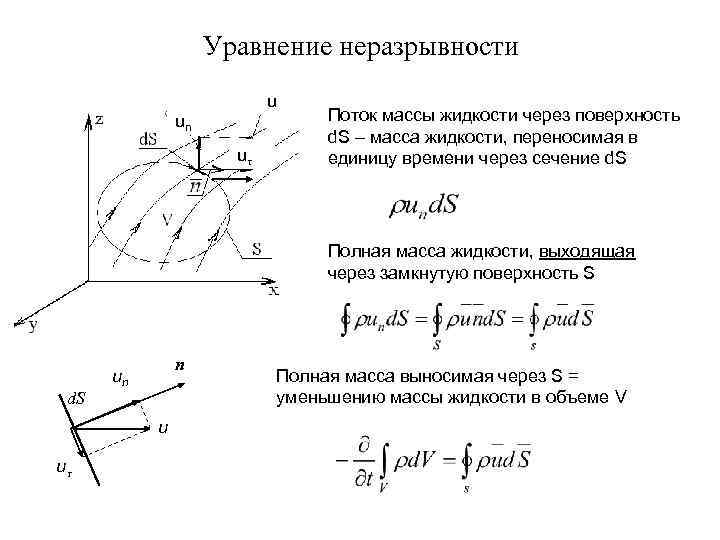Уравнение неразрывности un Поток массы жидкости через поверхность d. S – масса жидкости, переносимая в u единицу времени через сечение d. S Полная масса жидкости, выходящая через замкнутую поверхность S n un Полная масса выносимая через S = d. S уменьшению массы жидкости в объеме V u u

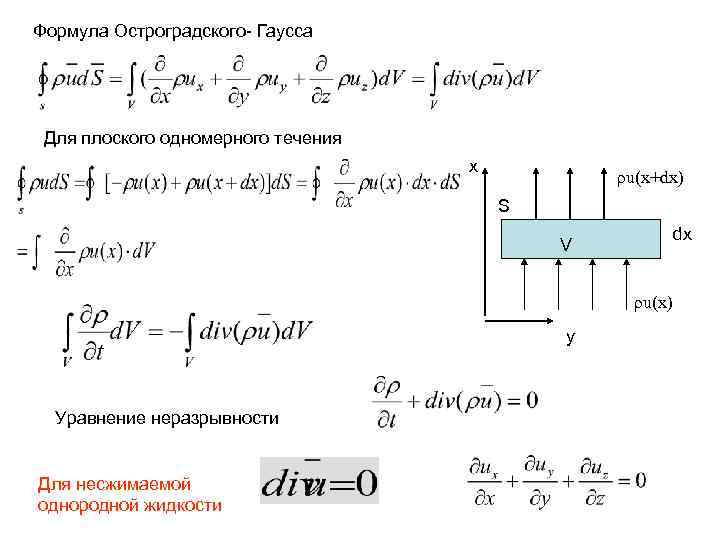Формула Остроградского- Гаусса Для плоского одномерного течения x ρu(x+dx) S dx V ρu(x) y Уравнение неразрывности Для несжимаемой однородной жидкости

Двумерные плоскопараллельные течения. Функция тока Плоское ( двумерное) течение: u=(ux, uy)=u(x, y, t) В двумерном случае Функция тока = (x, y, t) Полный дифференциал от Уравнение линий тока d вдоль линии тока

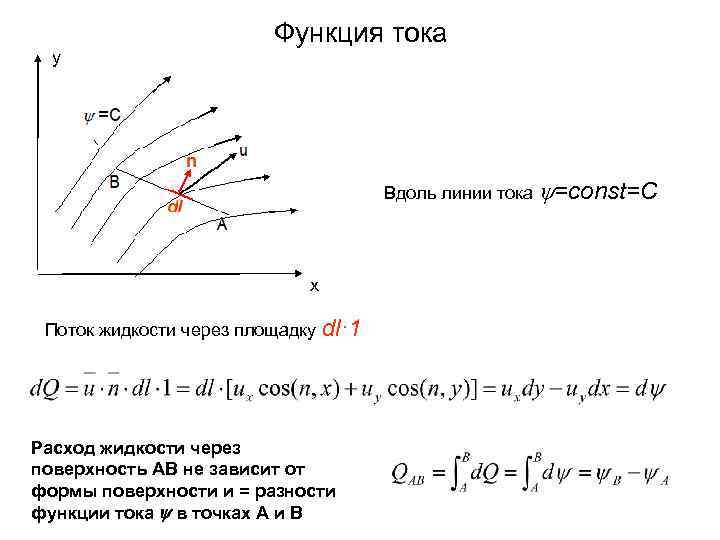Функция тока y Вдоль линии тока =const=C x Поток жидкости через площадку dl· 1 Расход жидкости через поверхность AB не зависит от формы поверхности и = разности функции тока в точках А и В

Функция тока (осесимметричный случай) Цилиндрические координаты x, r, θ x Пусть u=u(r, x) (θ) θ r Функция тока = (r, x) Уравнение линий тока *r =С вдоль линий (поверхностей) тока осесимметиричного течения