tema_4.ppt
- Количество слайдов: 60
 КИНЕМАТИКА ТОЧКИ Прямолинейное движение точки Закон движения. Положение точки М на прямой определяется ее расстоянием s = ОМ от некоторой фиксированной точки О— начала отсчета расстояний. Расстояние считается в одну сторону положительным, а в другую — отрицательным.
КИНЕМАТИКА ТОЧКИ Прямолинейное движение точки Закон движения. Положение точки М на прямой определяется ее расстоянием s = ОМ от некоторой фиксированной точки О— начала отсчета расстояний. Расстояние считается в одну сторону положительным, а в другую — отрицательным.
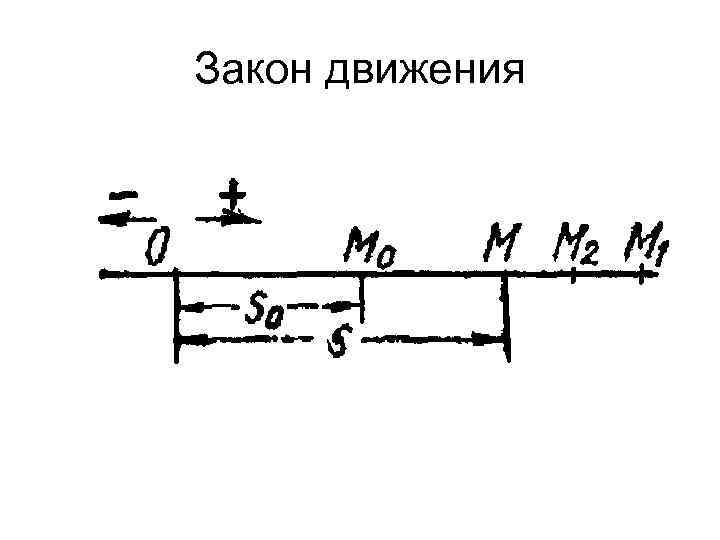 Закон движения
Закон движения
 Закон движения Если точка, выйдя в некоторый начальный момент времени t=0 из начального положения Мо, переместилась сначала в положение M 1, а затем в М 2, то расстояние М 0 М 2 называется перемещением точки, а арифметическая сумма M 0 M 1 + M 1 M 2 — ее путем.
Закон движения Если точка, выйдя в некоторый начальный момент времени t=0 из начального положения Мо, переместилась сначала в положение M 1, а затем в М 2, то расстояние М 0 М 2 называется перемещением точки, а арифметическая сумма M 0 M 1 + M 1 M 2 — ее путем.
 Закон движения дается либо уравнением s=f(t), либо таблицей соответствующих другу значений s и t, либо графически.
Закон движения дается либо уравнением s=f(t), либо таблицей соответствующих другу значений s и t, либо графически.
 Скорость Если s 1=f(t 1), s 2 =f (t 2), - то средней скоростью точки за промежуток времени t 2 – t 1 называется выражение v* = (s 2 – s 1)/( t 2 – t 1)
Скорость Если s 1=f(t 1), s 2 =f (t 2), - то средней скоростью точки за промежуток времени t 2 – t 1 называется выражение v* = (s 2 – s 1)/( t 2 – t 1)
 Скоростью точки в момент времени t называется v = lim ∆t-0 (∆S/∆t) = ds/dt
Скоростью точки в момент времени t называется v = lim ∆t-0 (∆S/∆t) = ds/dt
 Ускорение Если скорости v 1 и v 2 соответствуют моментам времени t 1 и t 2, то средним ускорением точки за промежуток времени t 1 - t 2 называется выражение a* = (v 2 – v 1)/( t 2 – t 1)
Ускорение Если скорости v 1 и v 2 соответствуют моментам времени t 1 и t 2, то средним ускорением точки за промежуток времени t 1 - t 2 называется выражение a* = (v 2 – v 1)/( t 2 – t 1)
 Ускорением точки в момент времени t называется a = lim ∆t-0(∆v/∆t) = dv/dt = d 2 s/dt 2 Скорость v и ускорение а иногда называются соответственно истинной скоростью и истинным ускорением.
Ускорением точки в момент времени t называется a = lim ∆t-0(∆v/∆t) = dv/dt = d 2 s/dt 2 Скорость v и ускорение а иногда называются соответственно истинной скоростью и истинным ускорением.
 Ускорение Если знаки v и a одинаковы, то скорость по абсолютной величине возрастает, и движение называется ускоренным, в противном случае — замедленным.
Ускорение Если знаки v и a одинаковы, то скорость по абсолютной величине возрастает, и движение называется ускоренным, в противном случае — замедленным.
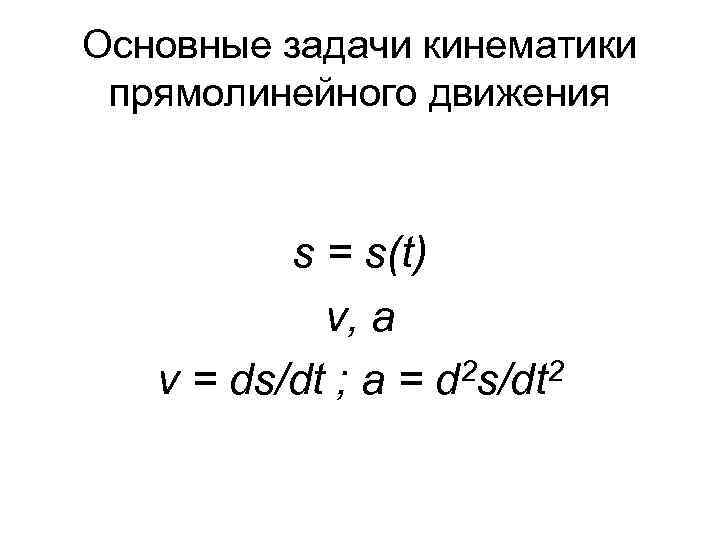 Основные задачи кинематики прямолинейного движения s = s(t) v, а v = ds/dt ; a = d 2 s/dt 2
Основные задачи кинематики прямолинейного движения s = s(t) v, а v = ds/dt ; a = d 2 s/dt 2
 Основные задачи кинематики прямолинейного движения v = v (t) s, a t v dt; a =dv/dt s = s 0 + 0∫
Основные задачи кинематики прямолинейного движения v = v (t) s, a t v dt; a =dv/dt s = s 0 + 0∫
 Основные задачи кинематики прямолинейного движения v = v (s) t, a s ds/v; a = v dv/ds t = s 0∫
Основные задачи кинематики прямолинейного движения v = v (s) t, a s ds/v; a = v dv/ds t = s 0∫
 Основные задачи кинематики прямолинейного движения а = a (t) V, S t a dt; s = s + ∫t v dt v = v 0 + 0∫ 0 0
Основные задачи кинематики прямолинейного движения а = a (t) V, S t a dt; s = s + ∫t v dt v = v 0 + 0∫ 0 0
 Основные задачи кинематики прямолинейного движения а = a (s) v, t 2 + 2 ∫s a ds); v = √ (v 0 s 0 t = s 0∫s ds/v
Основные задачи кинематики прямолинейного движения а = a (s) v, t 2 + 2 ∫s a ds); v = √ (v 0 s 0 t = s 0∫s ds/v
 Основные задачи кинематики прямолинейного движения а = a (v) s, t v v dv/a; t = ∫v dv/a s = s 0 + v 0∫ v 0
Основные задачи кинематики прямолинейного движения а = a (v) s, t v v dv/a; t = ∫v dv/a s = s 0 + v 0∫ v 0
 Частные случаи прямолинейного движения Равномерное движение (v = const): s = s 0 + v t; а=0
Частные случаи прямолинейного движения Равномерное движение (v = const): s = s 0 + v t; а=0
 Частные случаи прямолинейного движения Равномерно-переменное движение (а = const): v = v 0 + a t; 2/2 s = s 0 + v 0 t +а t
Частные случаи прямолинейного движения Равномерно-переменное движение (а = const): v = v 0 + a t; 2/2 s = s 0 + v 0 t +а t
 Частные случаи прямолинейного движения Свободное падение тел в безвоздушном пространстве у поверхности земли: h = g t 2/2; v = gt = √ 2 gh где h – высота падения; g - ускорение свободного падения
Частные случаи прямолинейного движения Свободное падение тел в безвоздушном пространстве у поверхности земли: h = g t 2/2; v = gt = √ 2 gh где h – высота падения; g - ускорение свободного падения
 Частные случаи прямолинейного движения Гармоническое колебательное движение - движение по закону синуса или косинуса: s = A sin (k t + β); s = A cos (k t + β);
Частные случаи прямолинейного движения Гармоническое колебательное движение - движение по закону синуса или косинуса: s = A sin (k t + β); s = A cos (k t + β);
 Гармоническое колебательное где: А — амплитуда колебания; k — круговая, угловая или циклическая частота колебания; угол φ = k t + β фаза колебания; β — начальная фаза колебания. Наименьший промежуток времени Т, через который движение воспроизводится, называется периодом колебания, а число колебаний в единицу времени — частотой колебания υ. υ = 1/Т = k/2π
Гармоническое колебательное где: А — амплитуда колебания; k — круговая, угловая или циклическая частота колебания; угол φ = k t + β фаза колебания; β — начальная фаза колебания. Наименьший промежуток времени Т, через который движение воспроизводится, называется периодом колебания, а число колебаний в единицу времени — частотой колебания υ. υ = 1/Т = k/2π
 Гармоническое колебательное Скорость и ускорение: v = A k cos (kt + β); a = - A k 2 sin (k t + β) = k 2 s
Гармоническое колебательное Скорость и ускорение: v = A k cos (kt + β); a = - A k 2 sin (k t + β) = k 2 s
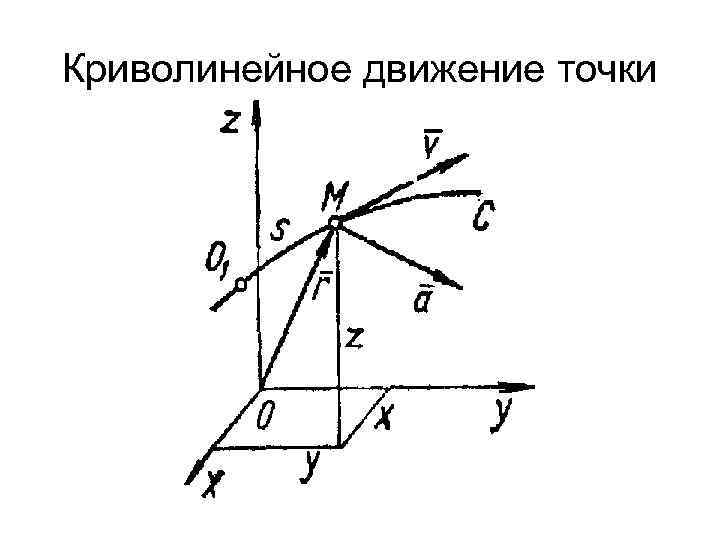
 Криволинейное движение точки Кривая С, которую описывает точка М при своем движении называется ее траекторией. На траектории устанавливается начало отсчета О 1 расстояние от которого по кривой в любой момент времени определяется законом движения по заданной траектории: s = f (t)
Криволинейное движение точки Кривая С, которую описывает точка М при своем движении называется ее траекторией. На траектории устанавливается начало отсчета О 1 расстояние от которого по кривой в любой момент времени определяется законом движения по заданной траектории: s = f (t)
 Криволинейное движение точки
Криволинейное движение точки
 Криволинейное движение точки Положение точки М определяется также либо радиусом-вектором r относительно некоторой точки О, либо координатами x, у, z по отношению к системе отсчета Oxyz. Тогда закон движения может быть задан тремя уравнениями: x = f 1(t); y=f 2(t); z=f 3(t) Исключив из них время, получаем уравнения траектории.
Криволинейное движение точки Положение точки М определяется также либо радиусом-вектором r относительно некоторой точки О, либо координатами x, у, z по отношению к системе отсчета Oxyz. Тогда закон движения может быть задан тремя уравнениями: x = f 1(t); y=f 2(t); z=f 3(t) Исключив из них время, получаем уравнения траектории.
 Криволинейное движение точки Скорость точки М в данный момент времени t выражается в векторной форме в алгебраической vs = ds / dt Вектор скорости направлен по касательной к траекторий
Криволинейное движение точки Скорость точки М в данный момент времени t выражается в векторной форме в алгебраической vs = ds / dt Вектор скорости направлен по касательной к траекторий
 Скорость точки проекции cкорости на оси координат vx = dx/dt; vy = dy/dt vz = dz/dt Величина скорости (модуль) v = [vs] = [ds/dt] = √(vx 2 + vy 2+ vz 2)
Скорость точки проекции cкорости на оси координат vx = dx/dt; vy = dy/dt vz = dz/dt Величина скорости (модуль) v = [vs] = [ds/dt] = √(vx 2 + vy 2+ vz 2)
 Скорость точки Направление вектора скорости определяется косинусами cos (v, x) = vx /v cos (v, у) = vy /v cos (v, z) = vz /v
Скорость точки Направление вектора скорости определяется косинусами cos (v, x) = vx /v cos (v, у) = vy /v cos (v, z) = vz /v
 Ускорение точки М в данный момент времени t выражается в векторной форме:
Ускорение точки М в данный момент времени t выражается в векторной форме:
 Ускорение Вектор ускорения лежит в соприкасающейся плоскости к траектории в данной точке и направлен в сторону вогнутости. Его проекции на оси координат и полное ускорение определяются аналогично определению скорости.
Ускорение Вектор ускорения лежит в соприкасающейся плоскости к траектории в данной точке и направлен в сторону вогнутости. Его проекции на оси координат и полное ускорение определяются аналогично определению скорости.
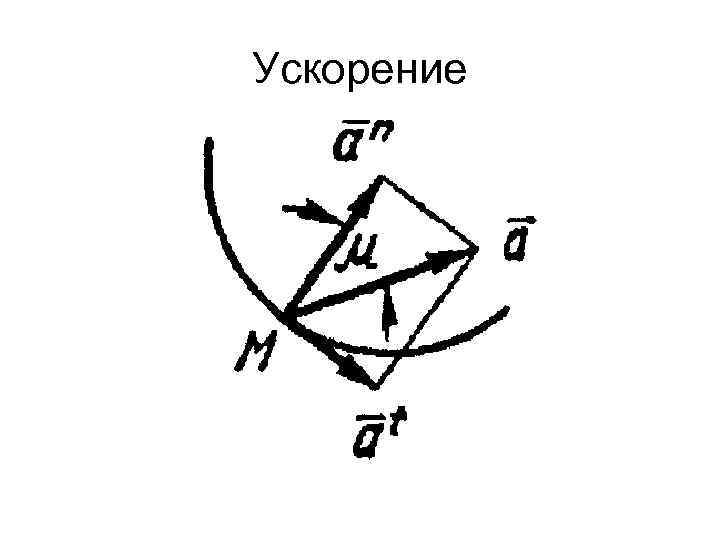
 Ускорение может быть разложено на тангенциальное аt (по касательной) и нормальное аn (по главной нормали ускорения).
Ускорение может быть разложено на тангенциальное аt (по касательной) и нормальное аn (по главной нормали ускорения).
 Ускорение
Ускорение
 Ускорение Проекции ускорения на касательную и главную нормаль равны: at = dvs/dt = d 2 s/dt 2 an = v 2/ρ где ρ-радиус кривизны траектории.
Ускорение Проекции ускорения на касательную и главную нормаль равны: at = dvs/dt = d 2 s/dt 2 an = v 2/ρ где ρ-радиус кривизны траектории.
 Ускорение Полное ускорение a = √( at)2 + (an)2 Его угол с нормалью μ = arctg (at/ an)
Ускорение Полное ускорение a = √( at)2 + (an)2 Его угол с нормалью μ = arctg (at/ an)
 Ускорение а образует острый угол со скоростью v в ускоренном движении и тупой - в замедленном, оно перпендикулярно v в равномерном движении или в моменты экстремума v; an исчезает в прямолинейном движении, в точке перегиба траектории, в начальный и конечный моменты криволинейного движения, а также в моменты мгновенной остановки точки.
Ускорение а образует острый угол со скоростью v в ускоренном движении и тупой - в замедленном, оно перпендикулярно v в равномерном движении или в моменты экстремума v; an исчезает в прямолинейном движении, в точке перегиба траектории, в начальный и конечный моменты криволинейного движения, а также в моменты мгновенной остановки точки.
 Движение точки в плоскости, отнесенное к полярным координатам. Закон движения точки определяется двумя уравнениями: r = f 1 (t) φ = f 2 (t) где угол φ, называемый полярным углом, принято измерять в радианах.
Движение точки в плоскости, отнесенное к полярным координатам. Закон движения точки определяется двумя уравнениями: r = f 1 (t) φ = f 2 (t) где угол φ, называемый полярным углом, принято измерять в радианах.
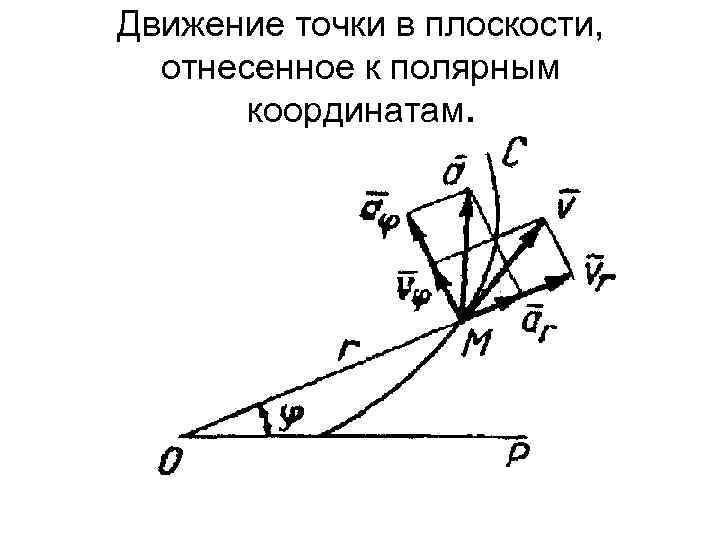 Движение точки в плоскости, отнесенное к полярным координатам.
Движение точки в плоскости, отнесенное к полярным координатам.
 Движение точки в плоскости, отнесенное к полярным координатам Средняя угловая скорость радиуса-вектора точки за промежуток времени t 2 -t 1 определяется выражением: ω* = (φ2 – φ 1)/( t 2 – t 1)
Движение точки в плоскости, отнесенное к полярным координатам Средняя угловая скорость радиуса-вектора точки за промежуток времени t 2 -t 1 определяется выражением: ω* = (φ2 – φ 1)/( t 2 – t 1)
 Движение точки в плоскости, отнесенное к полярным координатам Угловой скоростью (истинной угловой скоростью) радиусавектора точки в момент времени t называется ω = lim ∆t-0 (∆ φ /∆t) = d φ /dt
Движение точки в плоскости, отнесенное к полярным координатам Угловой скоростью (истинной угловой скоростью) радиусавектора точки в момент времени t называется ω = lim ∆t-0 (∆ φ /∆t) = d φ /dt
 Движение точки в плоскости, отнесенное к полярным координатам Средние угловое ускорение радиуса-вектора точки за промежуток времени t 2 -t 1 определяется выражением: ε* = (ω 2 – ω 1)/( t 2 – t 1)
Движение точки в плоскости, отнесенное к полярным координатам Средние угловое ускорение радиуса-вектора точки за промежуток времени t 2 -t 1 определяется выражением: ε* = (ω 2 – ω 1)/( t 2 – t 1)
 Движение точки в плоскости, отнесенное к полярным координатам Угловым ускорением (истинным угловым ускорением) радиусавектора точки в момент времени t называется ε = lim ∆t-0 (∆ ω /∆t) = dω /dt = d 2 φ /dt 2
Движение точки в плоскости, отнесенное к полярным координатам Угловым ускорением (истинным угловым ускорением) радиусавектора точки в момент времени t называется ε = lim ∆t-0 (∆ ω /∆t) = dω /dt = d 2 φ /dt 2
 Движение точки в плоскости, отнесенное к полярным координатам Проекции скорости и ускорения точки на направление радиуса-вектора называются соответственно радиальными скоростью vr и ускорением ar , а на направление перпендикулярное к радиусувектору, - трансверсальными скоростью vφ и ускорением aφ
Движение точки в плоскости, отнесенное к полярным координатам Проекции скорости и ускорения точки на направление радиуса-вектора называются соответственно радиальными скоростью vr и ускорением ar , а на направление перпендикулярное к радиусувектору, - трансверсальными скоростью vφ и ускорением aφ
 Движение точки в плоскости, отнесенное к полярным координатам Скорости определяются: vr = dr/dt; vφ = rω; v = √(vr )2 + (vφ )2
Движение точки в плоскости, отнесенное к полярным координатам Скорости определяются: vr = dr/dt; vφ = rω; v = √(vr )2 + (vφ )2
 Движение точки в плоскости, отнесенное к полярным координатам уcкорения определяются: ar= dr/dt; aφ = dr ω/dt + r ε a = √(ar )2 + (aφ )2
Движение точки в плоскости, отнесенное к полярным координатам уcкорения определяются: ar= dr/dt; aφ = dr ω/dt + r ε a = √(ar )2 + (aφ )2
 Движение точки по окружности Здесь радиальное направление прямо противоположно нормали, а трансверсальное совпадает с касательной.
Движение точки по окружности Здесь радиальное направление прямо противоположно нормали, а трансверсальное совпадает с касательной.
 Движение точки по окружности В этом случае r = ρ = R = const; vr = v = Rω; at = aφ = R ε; an = -ar = R ω2
Движение точки по окружности В этом случае r = ρ = R = const; vr = v = Rω; at = aφ = R ε; an = -ar = R ω2
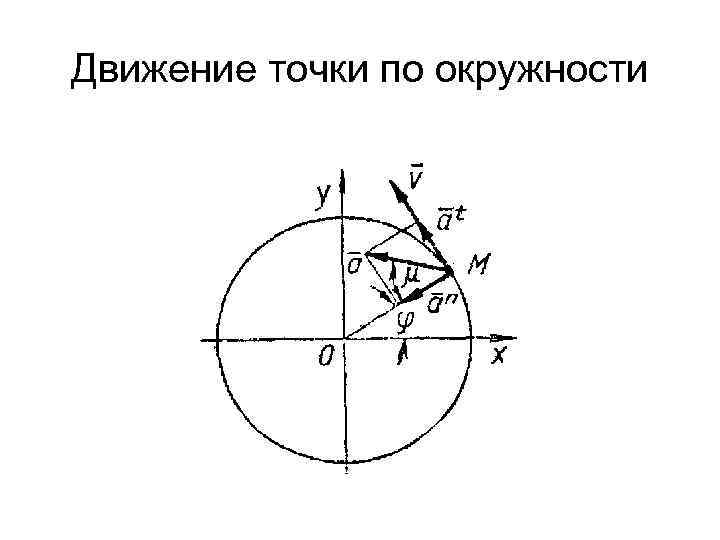 Движение точки по окружности
Движение точки по окружности
 Относительное движение точки Если точка М движется по отношению к системе отсчета Ωξήζ, которая, в свою очередь, движется по отношению к системе Oxzy, принятой за неподвижную, то движение точки М по отношению к системе Ωξήζ называется относительным, по отношению к системе Oxyz — абсолютным, а движение системы Ωξήζ по отношению к системе Oxyz — переносным или движением влечения.
Относительное движение точки Если точка М движется по отношению к системе отсчета Ωξήζ, которая, в свою очередь, движется по отношению к системе Oxzy, принятой за неподвижную, то движение точки М по отношению к системе Ωξήζ называется относительным, по отношению к системе Oxyz — абсолютным, а движение системы Ωξήζ по отношению к системе Oxyz — переносным или движением влечения.
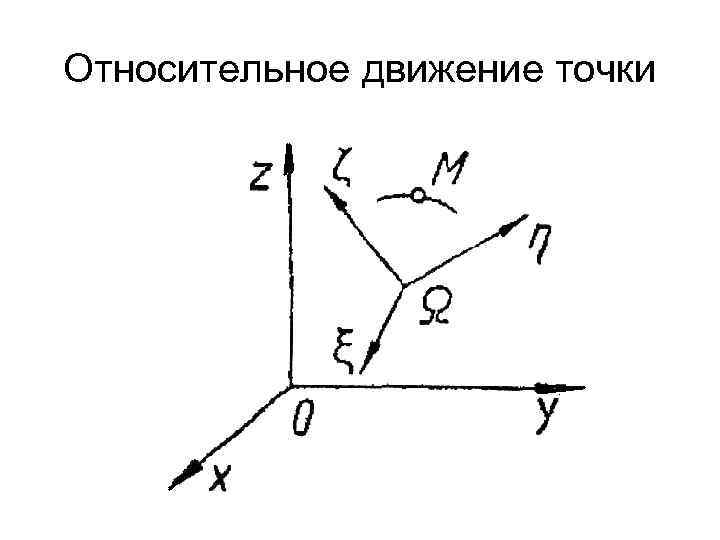 Относительное движение точки
Относительное движение точки
 Относительное движение точки Сложение скоростей. Абсолютная скорость точки равна геометрической сумме скоростей переносной и относительной
Относительное движение точки Сложение скоростей. Абсолютная скорость точки равна геометрической сумме скоростей переносной и относительной
 Относительное движение точки Сложение ускорений. Абсолютное ускорение точки равно геометрической сумме трех ускорений: переносного, относительного и поворотного или ускорения Кориолиса
Относительное движение точки Сложение ускорений. Абсолютное ускорение точки равно геометрической сумме трех ускорений: переносного, относительного и поворотного или ускорения Кориолиса
 КИНЕМАТИКА ТВЕРДОГО ТЕЛА Поступательное движение Поступательным движением твердого тела называется такое его движение, при котором всякая прямая, неизменно связанная с телом, перемещается параллельно самой себе.
КИНЕМАТИКА ТВЕРДОГО ТЕЛА Поступательное движение Поступательным движением твердого тела называется такое его движение, при котором всякая прямая, неизменно связанная с телом, перемещается параллельно самой себе.
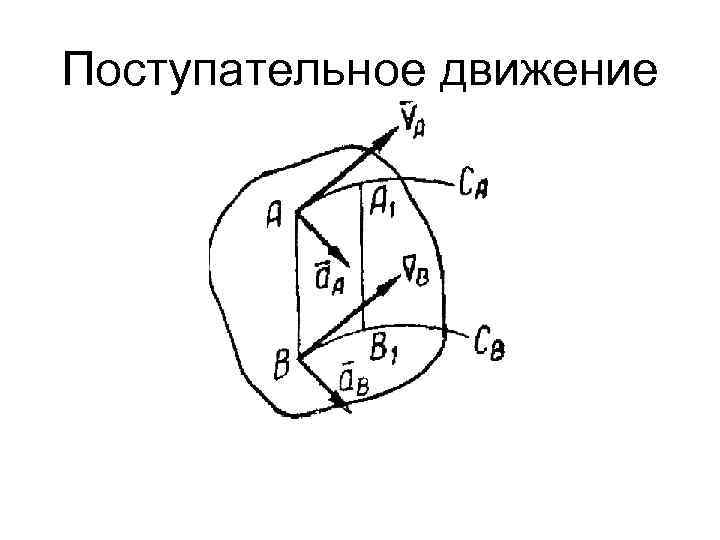 Поступательное движение
Поступательное движение
 Поступательное движение Скорости. Ускорения. При поступательном движении тела в любой момент времени все его точки имеют геометрически равные скорости (v. A = v. B) и геометрически равные ускорения (аа=ав). Следовательно, при поступательном движении все точки тела движутся одинаковым образом.
Поступательное движение Скорости. Ускорения. При поступательном движении тела в любой момент времени все его точки имеют геометрически равные скорости (v. A = v. B) и геометрически равные ускорения (аа=ав). Следовательно, при поступательном движении все точки тела движутся одинаковым образом.
 Вращение вокруг неподвижной оси Если тело имеет неподвижную ось АВ, то его положение в произвольный момент времени t определяется двугранным углом φ между начальным положением АМ 0 В некоторой плоскости, проходящей через ось вращения, и ее положением АМВ в данный момент.
Вращение вокруг неподвижной оси Если тело имеет неподвижную ось АВ, то его положение в произвольный момент времени t определяется двугранным углом φ между начальным положением АМ 0 В некоторой плоскости, проходящей через ось вращения, и ее положением АМВ в данный момент.
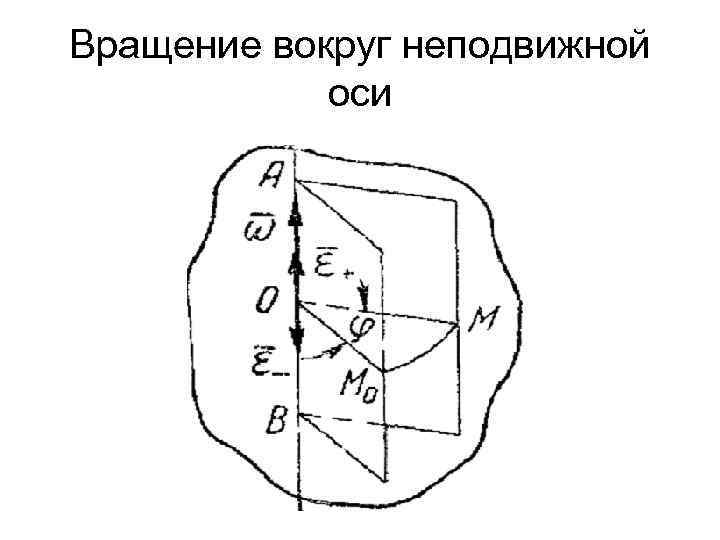 Вращение вокруг неподвижной оси
Вращение вокруг неподвижной оси
 Вращение вокруг неподвижной оси Скорости и ускорения точек вращающегося тела Здесь имеют место те же формулы, что и для кругового движения точки v = Rω; at = R ε; an = R ω 2
Вращение вокруг неподвижной оси Скорости и ускорения точек вращающегося тела Здесь имеют место те же формулы, что и для кругового движения точки v = Rω; at = R ε; an = R ω 2
 Винтовое движение Движение твердого тела, состоящее из вращательного и поступательного, направленного вдоль оси вращения, называется винтовым.
Винтовое движение Движение твердого тела, состоящее из вращательного и поступательного, направленного вдоль оси вращения, называется винтовым.
 Плоско-параллельное движение Плоско-параллельным движением твердого тела называется движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости. Это движение определяется движением плоской фигуры — проекции тела на плоскость, параллельно которой происходит движение.
Плоско-параллельное движение Плоско-параллельным движением твердого тела называется движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости. Это движение определяется движением плоской фигуры — проекции тела на плоскость, параллельно которой происходит движение.
 Плоско-параллельное движение Положение фигуры определяется X 0 , Yo произвольно выбранной точки — полюса и углом поворота вокруг полюса. Уравнения движения: х0 = f 1(t); у0 = f 2(t), φ= f 3(t)
Плоско-параллельное движение Положение фигуры определяется X 0 , Yo произвольно выбранной точки — полюса и углом поворота вокруг полюса. Уравнения движения: х0 = f 1(t); у0 = f 2(t), φ= f 3(t)
 Плоско-параллельное движение Скорость VM любой точки фигуры равна сумме скоростей полюса VО и скорости вращения VМО вокруг полюса. Ускорение определяется аналогичным образом. Точка скорость которой в данный момент равна нулю называется мгновенным центром скоростей
Плоско-параллельное движение Скорость VM любой точки фигуры равна сумме скоростей полюса VО и скорости вращения VМО вокруг полюса. Ускорение определяется аналогичным образом. Точка скорость которой в данный момент равна нулю называется мгновенным центром скоростей


