Кинематика.ppt
- Количество слайдов: 27
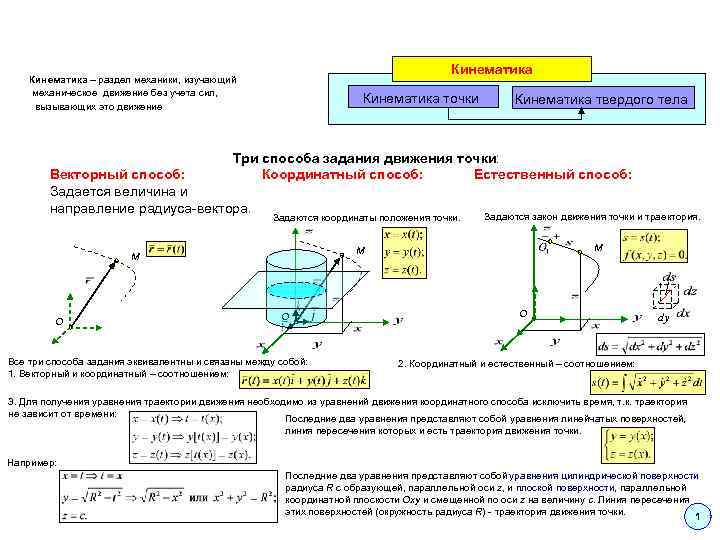
Кинематика – раздел механики, изучающий механическое движение без учета сил, вызывающих это движение Кинематика точки Кинематика твердого тела Три способа задания движения точки: Координатный способ: Естественный способ: Векторный способ: Задается величина и направление радиуса-вектора. Задаются координаты положения точки. M M M O Задаются закон движения точки и траектория. O Все три способа задания эквивалентны и связаны между собой: 1. Векторный и координатный – соотношением: O dy 2. Координатный и естественный – соотношением: 3. Для получения уравнения траектории движения необходимо из уравнений движения координатного способа исключить время, т. к. траектория не зависит от времени: Последние два уравнения представляют собой уравнения линейчатых поверхностей, линия пересечения которых и есть траектория движения точки. Например: Последние два уравнения представляют собой уравнения цилиндрической поверхности радиуса R c образующей, параллельной оси z, и плоской поверхности, параллельной координатной плоскости Oxy и смещенной по оси z на величину c. Линия пересечения этих поверхностей (окружность радиуса R) - траектория движения точки. 1
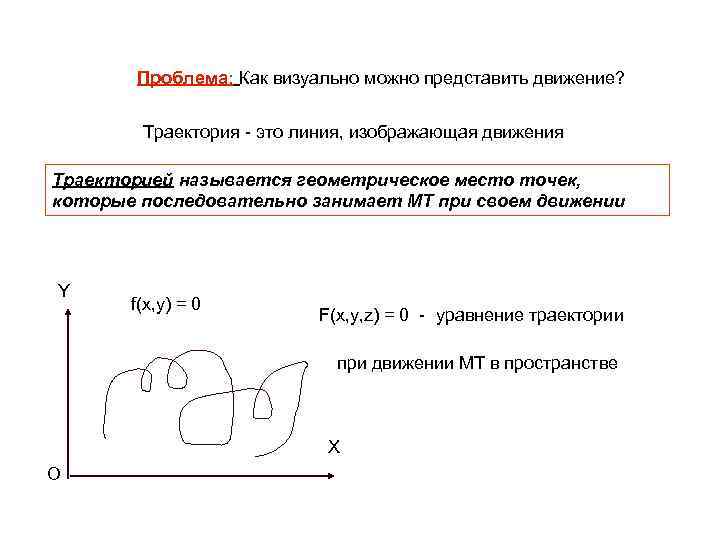
Проблема: Как визуально можно представить движение? Траектория - это линия, изображающая движения Траекторией называется геометрическое место точек, которые последовательно занимает МТ при своем движении Y f(x, y) = 0 F(x, y, z) = 0 - уравнение траектории при движении МТ в пространстве X О

Алгоритм получения уравнения траектории: Ø - записать закон движения, Ø- спроецировать его на оси системы координат, т. е. записать каждую проекцию радиус-вектора, как функцию времени, Ø- устранить время из этих уравнений , Ø- получить указанную функцию. Замечание: Траектория - не единственный способ визуализации движения. Можно использовать график зависимости координаты от времени, например, x(t) или y(t) и т. д. 3

Пример 1: Движение МТ по неподвижной окружности радиуса R. Равномерное: Y y(t) MT X 0 x(t) Возводим в квадрат слева и справа и суммируем: - уравнение траектории. 4

Пример 2. МТ движется в плоскости XY, причем закон движения выглядит так , где b и с есть константы. Найти траекторию. Из заданного закона движения x(t) = b t (1) и y(t) = c t 2 (2) Чтобы устранить время, из уравнения (1) выражаем t: и подставляем в (2): - искомое уравнение траектории Это есть уравнение параболы 5

Скорость точки – величина, характеризующая быстроту изменения положения точки в пространстве. Три способа задания движения точки определяют способы определения скорости точки: Векторный способ: Сравним два положения точки в моменты времени t 1= t + t: M - вектор средней скорости в интервале времени t, направлен по направлению вектора перемещения (хорде MM 1). Предел отношения приращения функции Устремим t 0 и перейдем к приращению приращения аргумента есть к пределу: производная функции (по определению): - вектор истинной скорости точки в момент времени t, направлен по касательной к траектории (при приближении M 1 к M хорда занимает положение касательной). M 1 O Координатный способ: Связь радиуса-вектора с координатами определяется выражением: Используем векторную форму определения скорости: M Компоненты (составляющие) вектора скорости: Проекции скорости на оси координат: O Используем векторную форму определения скорости: Естественный способ: Представим производную радиус-вектора как предел: M M 1 O Представим радиус-вектор как сложную функцию: Вектор приращения радиуса-вектора направлен по хорде MM 1 и в пределе занимает положение касательной. Величина производной радиуса-вектора по дуговой координате равна 1: Таким образом, производная радиуса-вектора по дуговой координате есть единичный вектор, направленный по касательной к траектории. Вектор скорости равен: При s 0 радиус кривизны 1 , угол между радиусами кривизны 0, числитель - основание равнобедренного треугольника, знаменатель – длина круговой дуги радиуса . Проекция скорости на касательную: При вектор скорости направлен в сторону увеличения дуговой координаты, В противном случае – в обратную сторону. 2


Ускорение точки – величина, характеризующая быстроту изменения скорости точки. Три способа задания движения точки определяют способы определения ускорения точки: Векторный способ: Сравним скорости точки в двух положениях точки в моменты времени t 1= t + t: M - вектор среднего ускорения в интервале времени t, направлен в сторону вогнутости траектории. M 1 Переходя к пределу получаем: - вектор истинного ускорения точки в момент времени t, лежит в соприкасающейся плоскости (предельное положение плоскости, проведенной O через касательную в точке M и прямую, параллельную касательной в точке M 1, при стремлении M 1 к M) и направлен в сторону вогнутости траектории. Координатный способ: Используем полученное векторное выражение и связь радиуса-вектора с координатами M Компоненты (составляющие) вектора ускорения: Проекции ускорения на оси координат: O Таким образом полное ускорение точки есть векторная сумма двух ускорений: Естественный способ: Используем векторное выражение для ускорения и выражение для скорости при естественной способе задания: касательного, направленного по касательной к траектории в сторону увеличения дуговой координаты, если (в противном случае – в противоположную) и Представим единичный Производная единичного нормального ускорения, направленного по нормали к касательной в сторону центра M касательный вектор касательного вектора: кривизны (вогнутости траектории): как сложную функцию: Величина производной Таким образом, производная M 1 единичного касательного вектора Модуль полного ускорения: по дуговой координате есть вектор, направленный перпендикулярно При s 0 радиус кривизны 1 , угол Угол между приращением касательной к траектории. Введем единичный вектор n, нормальный (перпендикулярный) к касательной, O между радиусами кривизны единичного вектора направленный к центру кривизны. 0, числитель Компоненты Проекции -основание равнобедренного треугольника, и самим вектором С использованием вектора n и ранее (составляющие) образованного единичными векторами 1 и , при 0, стремится к 90 о. ускорения определенных величин вектора 3 знаменатель – длина круговой дуги радиуса на оси и n: ускорение представляется как сумма векторов: . ускорения:
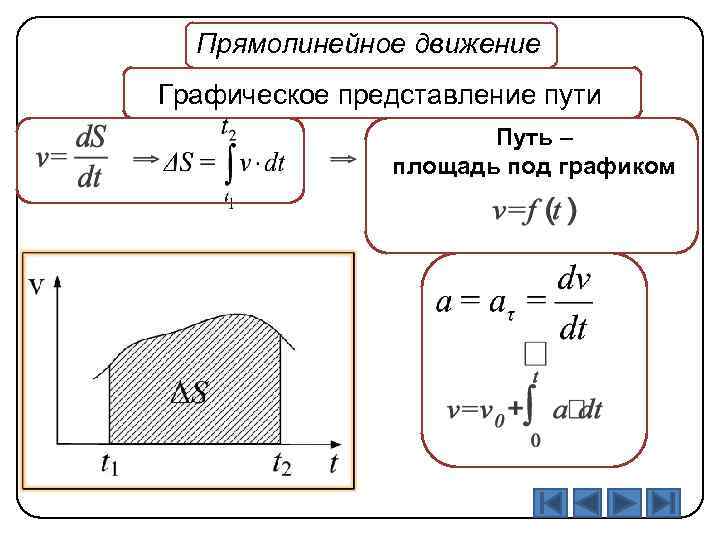
Прямолинейное движение Графическое представление пути Путь – площадь под графиком
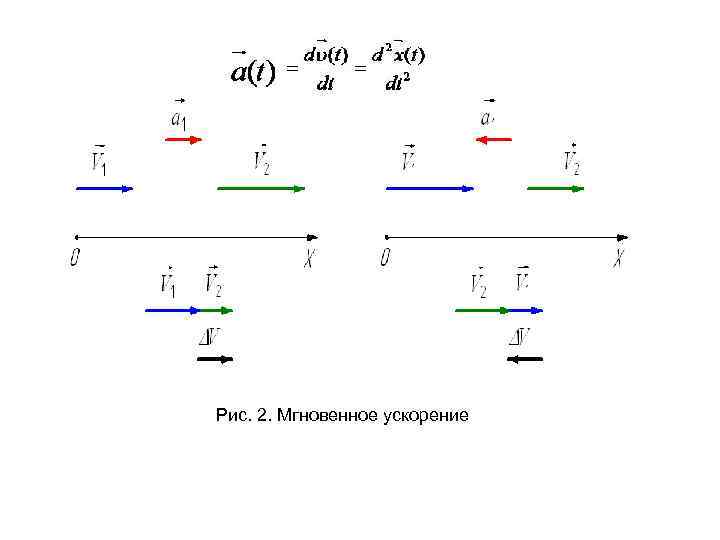
Рис. 2. Мгновенное ускорение
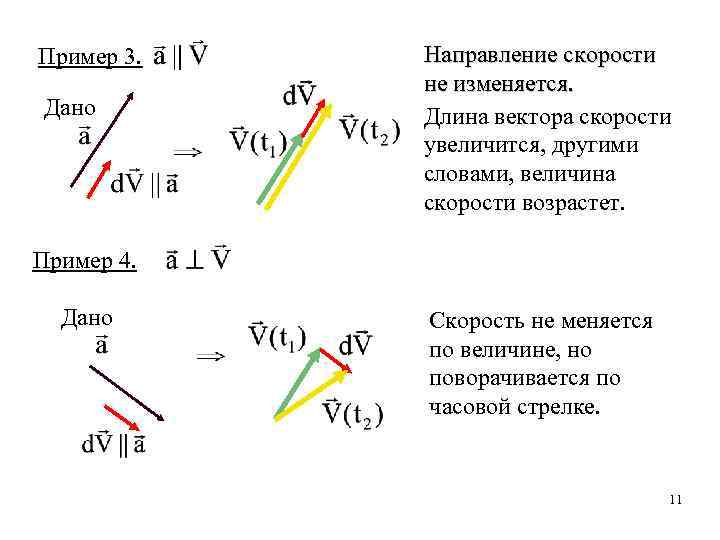
Пример 3. Дано Направление скорости не изменяется. Длина вектора скорости увеличится, другими словами, величина скорости возрастет. Пример 4. Дано Скорость не меняется по величине, но поворачивается по часовой стрелке. 11
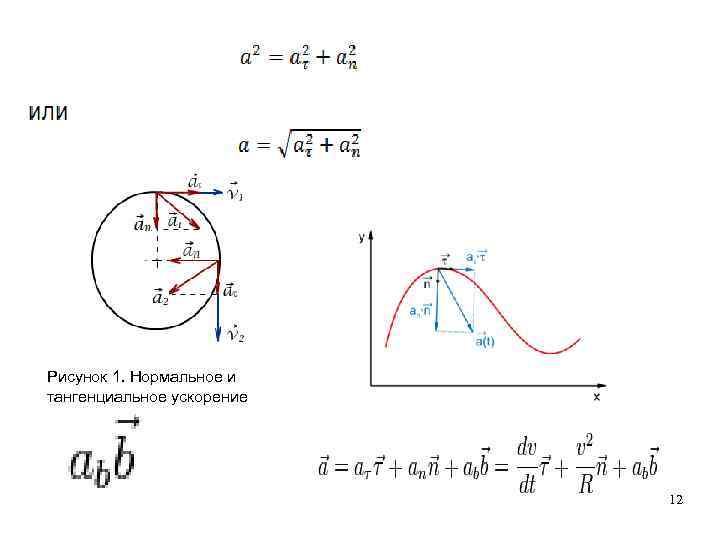
Рисунок 1. Нормальное и тангенциальное ускорение 12

Равнопеременное движение точки – движение точки по траектории, при котором касательное ускорение не изменяется по величине. Запишем выражение для касательного ускорения через проекцию скорости: Полученное выражение есть дифференциальное уравнение, которое легко решается разделением переменных и интегрированием левой и правой частей: -скорость точки при равнопеременном движении В свою очередь скорость точки также связывается с дуговой координатой дифференциальной зависимостью: После подстановки выражения для скорости и интегрирования получаем : - дуговая координата точки при равнопеременном движении 4

Произвольное криволинейное движение
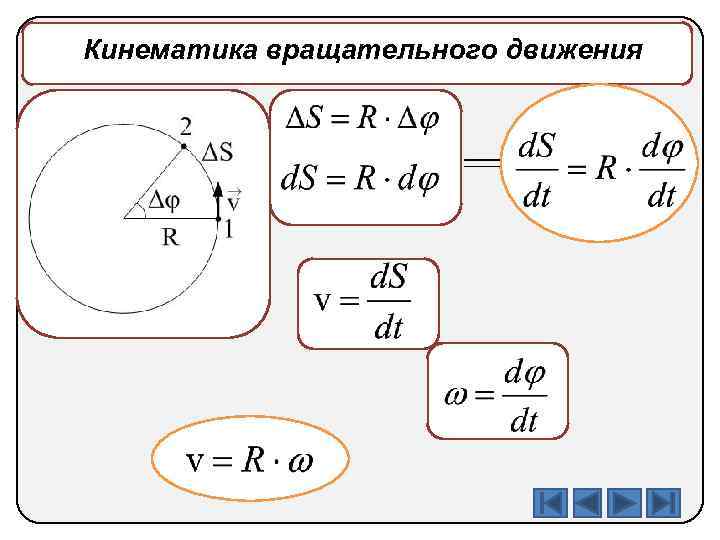
Кинематика вращательного движения
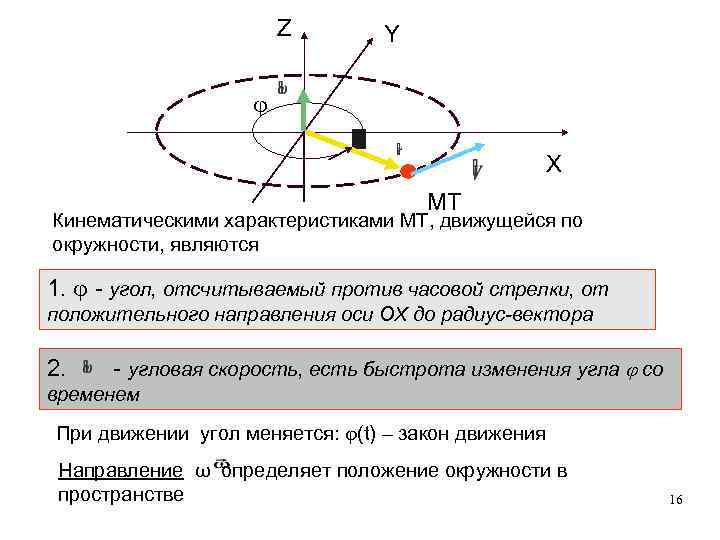
Z Y X MT Кинематическими характеристиками МТ, движущейся по окружности, являются 1. - угол, отсчитываемый против часовой стрелки, от положительного направления оси ОХ до радиус-вектора 2. - угловая скорость, есть быстрота изменения угла со временем При движении угол меняется: (t) – закон движения Направление ω определяет положение окружности в пространстве 16

Это направление определяется правилом правого винта: рукоятка винта движется вместе с материальной точкой по окружности, стержень винта движется вдоль. Плоскость окружности всегда перпендикулярна вектору угловой скорости. Величина угловой скорости 3. - угловое ускорение показывает как быстро и в каком направлении меняется вектор угловой скорости 17
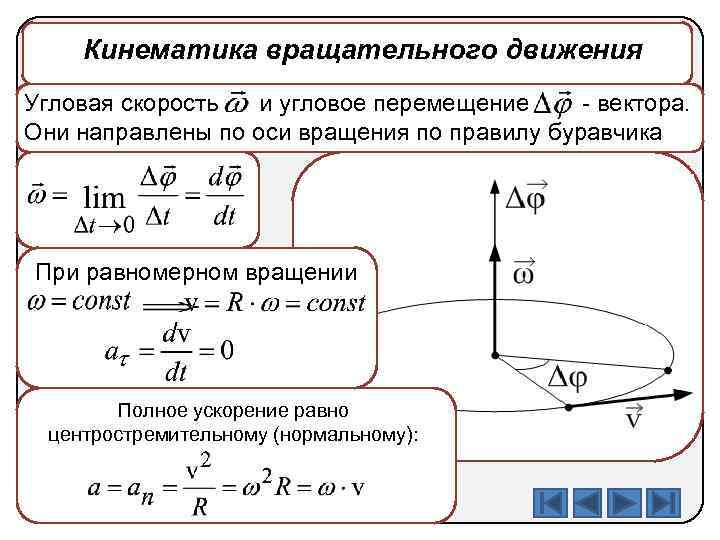
Кинематика вращательного движения Угловая скорость и угловое перемещение - вектора. Они направлены по оси вращения по правилу буравчика При равномерном вращении Полное ускорение равно центростремительному (нормальному):

Кинематика вращательного движения При неравномерном вращении Угловое ускорение показывает быстроту изменения угловой скорости

Связь угловых и линейных кинематических характеристик При движении МТ по окружности можно использовать два набора кинематических характеристик МТ: линейные угловые Проблема: Как связаны друг с другом угловые и линейные характеристики при движении МТ по окружности? ЗАДАЧА: Найти связь Для проекций радиус-вектора 20


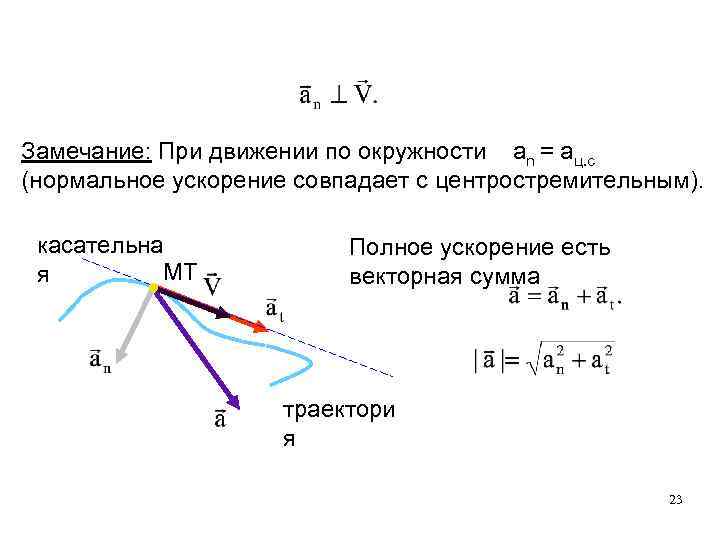
Вектор нормального ускорения не меняет величины скорости. Замечание: При движении по окружности an = aц. с (нормальное ускорение совпадает с центростремительным). касательна МТ я Полное ускорение есть векторная сумма траектори я 23
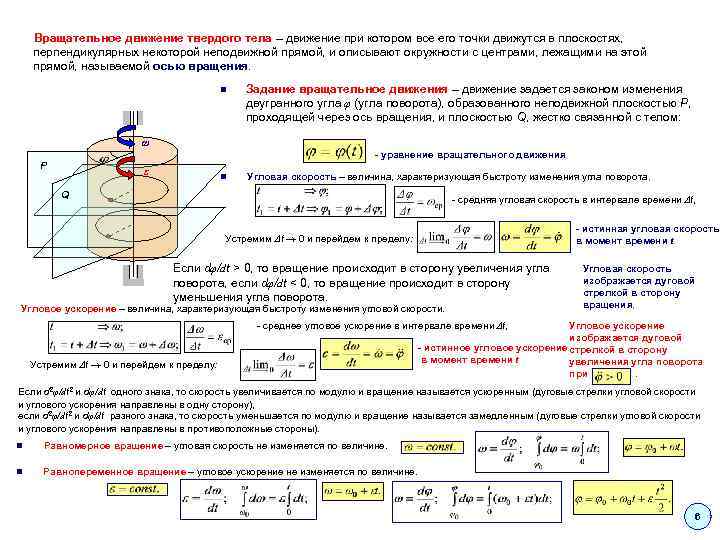
Вращательное движение твердого тела – движение при котором все его точки движутся в плоскостях, перпендикулярных некоторой неподвижной прямой, и описывают окружности с центрами, лежащими на этой прямой, называемой осью вращения. ω P Задание вращательное движения – движение задается законом изменения двугранного угла φ (угла поворота), образованного неподвижной плоскостью P, проходящей через ось вращения, и плоскостью Q, жестко связанной с телом: - уравнение вращательного движения ε Угловая скорость – величина, характеризующая быстроту изменения угла поворота. Q - средняя угловая скорость в интервале времени t, - истинная угловая скорость в момент времени t Устремим t 0 и перейдем к пределу: Если dφ/dt > 0, то вращение происходит в сторону увеличения угла поворота, если dφ/dt < 0, то вращение происходит в сторону уменьшения угла поворота. Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости. Угловая скорость изображается дуговой стрелкой в сторону вращения. - среднее угловое ускорение в интервале времени t, Устремим t 0 и перейдем к пределу: Угловое ускорение изображается дуговой - истинное угловое ускорение стрелкой в сторону в момент времени t увеличения угла поворота при. Если d 2φ/dt 2 и dφ/dt одного знака, то скорость увеличивается по модулю и вращение называется ускоренным (дуговые стрелки угловой скорости и углового ускорения направлены в одну сторону), если d 2φ/dt 2 и dφ/dt разного знака, то скорость уменьшается по модулю и вращение называется замедленным (дуговые стрелки угловой скорости и углового ускорения направлены в противоположные стороны). Равномерное вращение – угловая скорость не изменяется по величине. Равнопеременное вращение – угловое ускорение не изменяется по величине. 6

Скорость точки при вращательном движении твердого тела – траектория точки известна (окружность радиуса R – расстояние точки до оси вращения), можно применить формулу для определения скорости точки при естественном задании движения: Дуговая координата связана с радиусом окружности: - O + s R φ ε ω Тогда проекция скорости на касательную к окружности: Поскольку далее работают с модулем угловой скорости после изображения ее в виде дуговой стрелки расчетной формулой является выражение для модуля скорости: и вектор скорости направляют перпендикулярно радиусу в сторону дуговой стрелки угловой скорости. Как следует из формулы скорость точки пропорциональна расстоянию ее до оси вращения (радиусу вращения). Ускорение точки при вращательном движении твердого тела – траектория точки известна, можно применить формулы для определения ускорений точки при естественном задании движения: Тогда проекции ускорения на касательную к окружности и нормаль: Поскольку далее работают с модулем углового ускорения после изображения его в виде дуговой стрелки расчетной формулой является выражение для касательного ускорения: и вектор этого ускорения, называемого вращательным ускорением, направляют перпендикулярно радиусу в сторону дуговой стрелки углового ускорения. z z Нормальное ускорение теперь называется осестремительным ускорением , его направляют по радиусу к оси вращения независимо от направления дуговой стрелки угловой скорости, не говоря уж о направлении дуговой стрелки углового ускорения. ω Как следует из формул оба ускорения точки пропорциональны расстоянию ее до оси вращения (радиусу вращения). Полное ускорение точки, как и ранее, есть векторная сумма этих ускорений: ω Угол между направлением полного ускорения и радиусом от величины радиуса не зависит и ε ε равен: Скорость и ускорения точки при вращательном движении как векторные произведения. Представим угловую скорость и угловое ускорения как векторы, направленные по оси вращения в ту сторону, откуда дуговые стрелки этих величин указывают вращение против часовой стрелки. Положительное направление оси z можно задать с помощью единичного вектора k, тогда векторы угловой скорости и углового ускорения можно представить как: где z, z – проекции соответствующих векторов на ось z. 7
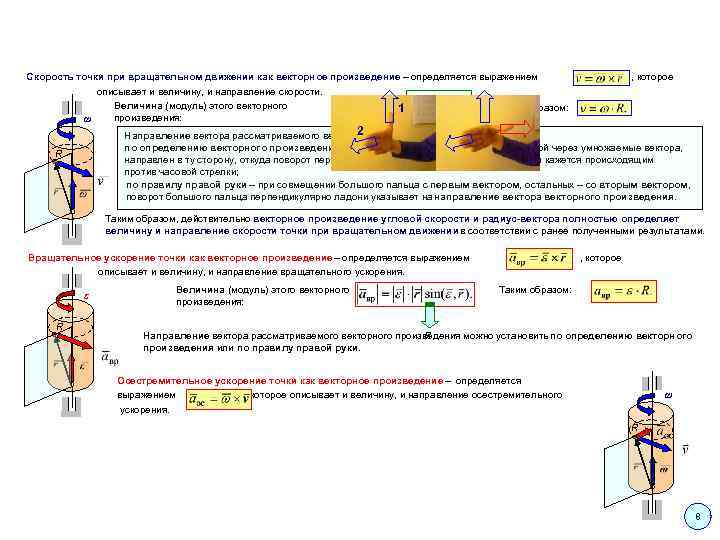
Скорость точки при вращательном движении как векторное произведение – определяется выражением описывает и величину, и направление скорости. Величина (модуль) этого векторного Таким образом: 1 произведения: ω , которое 2 Направление вектора рассматриваемого векторного произведения: R по определению векторного произведения – перпендикулярно плоскости, проведенной через умножаемые вектора, направлен в ту сторону, откуда поворот первого вектора ко второму на наименьший угол кажется происходящим против часовой стрелки; по правилу правой руки – при совмещении большого пальца с первым вектором, остальных – со вторым вектором, поворот большого пальца перпендикулярно ладони указывает на направление вектора векторного произведения. R Таким образом, действительно векторное произведение угловой скорости и радиус-вектора полностью определяет величину и направление скорости точки при вращательном движении в соответствии с ранее полученными результатами. Вращательное ускорение точки как векторное произведение – определяется выражением описывает и величину, и направление вращательного ускорения. ε R Величина (модуль) этого векторного произведения: , которое Таким образом: R Направление вектора рассматриваемого векторного произведения можно установить по определению векторного произведения или по правилу правой руки. Осестремительное ускорение точки как векторное произведение – определяется выражением , которое описывает и величину, и направление осестремительного ускорения. ω R 8

Таким образом, действительно векторное произведение углового ускорения и радиус-вектора полностью определяет величину и направление вращательного ускорения точки в соответствии с ранее полученными результатами. Величина (модуль) этого векторного произведения: Таким образом: Направление вектора рассматриваемого векторного произведения можно установить по определению векторного произведения или по правилу правой руки. Это векторное произведение может быть также записано в виде:
Кинематика.ppt