 кинематика 1, 2, 3, 4, 5
кинематика 1, 2, 3, 4, 5
 1. 1. 1. Задачи кинематики Кинематика – это раздел теоретической механики, в котором изучается движение тела с геометрической точки зрения, т. е. без учета сил, действующих на тело Движение материальной точки – это изменение ее положения относительно какого-либо другого тела (тела отсчета) с течением времени Положение объекта задается расстоянием до некоторого другого объекта и является относительным. Относительным является и само движение Задачи кинематики 1. Определение математических способов задания движения тела 2. Определение для заданного способа задания движения тела его кинематических характеристик 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 5
1. 1. 1. Задачи кинематики Кинематика – это раздел теоретической механики, в котором изучается движение тела с геометрической точки зрения, т. е. без учета сил, действующих на тело Движение материальной точки – это изменение ее положения относительно какого-либо другого тела (тела отсчета) с течением времени Положение объекта задается расстоянием до некоторого другого объекта и является относительным. Относительным является и само движение Задачи кинематики 1. Определение математических способов задания движения тела 2. Определение для заданного способа задания движения тела его кинематических характеристик 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 5
 1. 1. 2. Пространство и время • Постулируется существование не связанных между собой абсолютного пространства и абсолютного времени • Свойства пространства и времени не зависят и от того, как движутся тела • Пространство является трехмерным евклидовым пространством, оно однородное и изотропное • Время также однородное и одинаково во всех точках пространства • Время изменяется непрерывно, а наблюдатель измеряет "расстояние" между различными моментами времени часами • Часы универсальны и их показания не зависят от того, расположены они в покоящихся или движущихся объектах • Однородность времени означает отсутствие выделенных моментов времени. Выбор начала отсчета времени поэтому диктуется лишь конкретной решаемой задачей 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 6
1. 1. 2. Пространство и время • Постулируется существование не связанных между собой абсолютного пространства и абсолютного времени • Свойства пространства и времени не зависят и от того, как движутся тела • Пространство является трехмерным евклидовым пространством, оно однородное и изотропное • Время также однородное и одинаково во всех точках пространства • Время изменяется непрерывно, а наблюдатель измеряет "расстояние" между различными моментами времени часами • Часы универсальны и их показания не зависят от того, расположены они в покоящихся или движущихся объектах • Однородность времени означает отсутствие выделенных моментов времени. Выбор начала отсчета времени поэтому диктуется лишь конкретной решаемой задачей 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 6
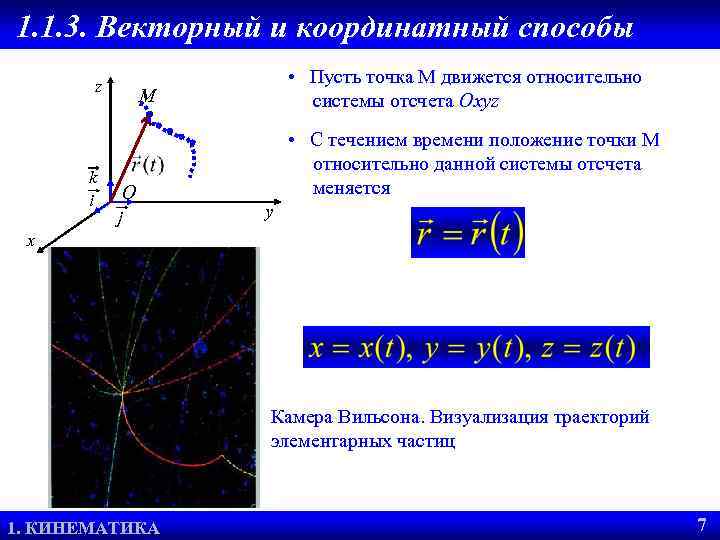 1. 1. 3. Векторный и координатный способы z k i • Пусть точка М движется относительно системы отсчета Oxyz М O j • С течением времени положение точки М относительно данной системы отсчета меняется y x Камера Вильсона. Визуализация траекторий элементарных частиц 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ 1. КИНЕМАТИКА ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 7
1. 1. 3. Векторный и координатный способы z k i • Пусть точка М движется относительно системы отсчета Oxyz М O j • С течением времени положение точки М относительно данной системы отсчета меняется y x Камера Вильсона. Визуализация траекторий элементарных частиц 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ 1. КИНЕМАТИКА ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 7
 1. 1. 4. Естественный способ задания А – О + s s = s(t) • Пусть точка М движется вдоль траектории АВ • Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета M • . Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления • Введем криволинейную координату s, длину B криволинейного отрезка ОМ, взятую с соответствующим знаком Закон движения точки вдоль траектории M • Стоит заметить, что уравнение s = s(t) – + О определяет положение точки на M s траектории, а не путь, пройденный ею M 1 • Пройденный путь равен 2. 1. ОПРЕДЕЛЕНИЕ ССС ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. ЕСТЕСТВЕННЫЙ СПОСОБ 1. КИНЕМАТИКА 8
1. 1. 4. Естественный способ задания А – О + s s = s(t) • Пусть точка М движется вдоль траектории АВ • Выберем на этой траектории какую-нибудь точку О, которую примем за начало отсчета M • . Будем считать траекторию криволинейной координатной осью и установим на ней положительное и отрицательное направления • Введем криволинейную координату s, длину B криволинейного отрезка ОМ, взятую с соответствующим знаком Закон движения точки вдоль траектории M • Стоит заметить, что уравнение s = s(t) – + О определяет положение точки на M s траектории, а не путь, пройденный ею M 1 • Пройденный путь равен 2. 1. ОПРЕДЕЛЕНИЕ ССС ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. ЕСТЕСТВЕННЫЙ СПОСОБ 1. КИНЕМАТИКА 8
 1. 1. 6. Связь естественного и координатного способов z • Пусть точка M движется вдоль траектории АВ A – O • Приращение траектории s за время t равно Δs + М Δx Δz О Δy При B y x • Координаты s, x, y, z – функции времени где 2. 1. ОПРЕДЕЛЕНИЕ ССС • 1. КИНЕМАТИКА Коэффициент трения покоя 9
1. 1. 6. Связь естественного и координатного способов z • Пусть точка M движется вдоль траектории АВ A – O • Приращение траектории s за время t равно Δs + М Δx Δz О Δy При B y x • Координаты s, x, y, z – функции времени где 2. 1. ОПРЕДЕЛЕНИЕ ССС • 1. КИНЕМАТИКА Коэффициент трения покоя 9
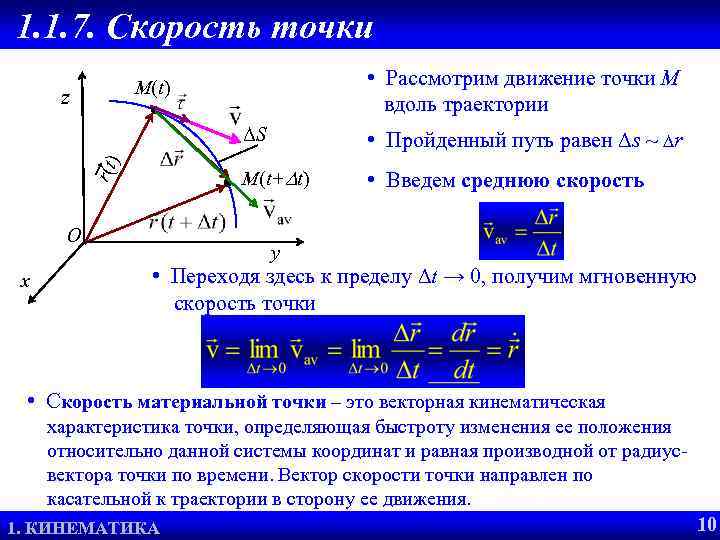 1. 1. 7. Скорость точки • Рассмотрим движение точки М вдоль траектории M(t) z О x • Пройденный путь равен s ~ r M(t+ t) r (t ) ΔS • Введем среднюю скорость y • Переходя здесь к пределу t → 0, получим мгновенную скорость точки • Скорость материальной точки – это векторная кинематическая характеристика точки, определяющая быстроту изменения ее положения относительно данной системы координат и равная производной от радиус вектора точки по времени. Вектор скорости точки направлен по касательной к траектории в сторону ее движения. 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 10
1. 1. 7. Скорость точки • Рассмотрим движение точки М вдоль траектории M(t) z О x • Пройденный путь равен s ~ r M(t+ t) r (t ) ΔS • Введем среднюю скорость y • Переходя здесь к пределу t → 0, получим мгновенную скорость точки • Скорость материальной точки – это векторная кинематическая характеристика точки, определяющая быстроту изменения ее положения относительно данной системы координат и равная производной от радиус вектора точки по времени. Вектор скорости точки направлен по касательной к траектории в сторону ее движения. 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 10
 1. 1. 8. Ускорение точки • Как определить быстроту изменения скорости точки? • Пусть материальная точка М движется вдоль траектории M(t) M(t+ t) • Определим приращение скорости за время t • Определим среднее ускорение • Переходя здесь к пределу t → 0, получим мгновенное ускорение точки • Таким образом, ускорение точки – это векторная кинематическая величина, характеризующая быстроту изменения ее скорости и равная первой производной от скорости или второй производной от радиус-вектора по времени 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 11
1. 1. 8. Ускорение точки • Как определить быстроту изменения скорости точки? • Пусть материальная точка М движется вдоль траектории M(t) M(t+ t) • Определим приращение скорости за время t • Определим среднее ускорение • Переходя здесь к пределу t → 0, получим мгновенное ускорение точки • Таким образом, ускорение точки – это векторная кинематическая величина, характеризующая быстроту изменения ее скорости и равная первой производной от скорости или второй производной от радиус-вектора по времени 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 11
 1. 1. 9. Тангенциальное и нормальное ускорение Т. о. , где ω = v/ρ – тангенциальное ускорение, характеризующее изменение скорости по величине – нормальное ускорение, характеризующее изменение скорости по направлению 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 12
1. 1. 9. Тангенциальное и нормальное ускорение Т. о. , где ω = v/ρ – тангенциальное ускорение, характеризующее изменение скорости по величине – нормальное ускорение, характеризующее изменение скорости по направлению 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 12
 6
6
 1. 1. 10. Оси естественного трехгранника Спрямляющая плоскость O + В этой системе координат М – Аналогично ускорение Нормальная плоскость 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА ТОЧКИ Соприкасающаяся плоскость 13
1. 1. 10. Оси естественного трехгранника Спрямляющая плоскость O + В этой системе координат М – Аналогично ускорение Нормальная плоскость 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА ТОЧКИ Соприкасающаяся плоскость 13
 1. 4. 3. Теорема о сложении скоростей M z z 1 y 1 O 1 x 1 O y x • Если точка М не движется относительно подвижной системы отсчета, то , и ее абсолютная скорость совпадает тогда со скоростью движения подвижной системы отсчета относительно неподвижной • По определению это и есть скорость переносного движения Теорема. Абсолютная скорость точки равна сумме относительной и переносной скоростей 2. 1. ОПРЕДЕЛЕНИЕ ССС СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 11. КИНЕМАТИКА 38
1. 4. 3. Теорема о сложении скоростей M z z 1 y 1 O 1 x 1 O y x • Если точка М не движется относительно подвижной системы отсчета, то , и ее абсолютная скорость совпадает тогда со скоростью движения подвижной системы отсчета относительно неподвижной • По определению это и есть скорость переносного движения Теорема. Абсолютная скорость точки равна сумме относительной и переносной скоростей 2. 1. ОПРЕДЕЛЕНИЕ ССС СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 11. КИНЕМАТИКА 38
 1. 4. 4. Теорема Кориолиса • Если точка покоится относительно подвижной системы отсчета, то ее движение совпадает с переносным движением, а абсолютное ускорение – с переносным ускорением Теорема. Абсолютное ускорение точки равно сумме относительного , переносного и кориолисова ускорений 2. 1. КИНЕМАТИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 1. ОПРЕДЕЛЕНИЕ ССС 39
1. 4. 4. Теорема Кориолиса • Если точка покоится относительно подвижной системы отсчета, то ее движение совпадает с переносным движением, а абсолютное ускорение – с переносным ускорением Теорема. Абсолютное ускорение точки равно сумме относительного , переносного и кориолисова ускорений 2. 1. КИНЕМАТИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 1. ОПРЕДЕЛЕНИЕ ССС 39
 1. 3. 5. Ускорение Кориолиса Это ускорение обращается в нуль, если Гюстав Гаспар Кориолис 1792 -1843 • угловая скорость подвижной системы отсчета равна нулю ω=0, т. е. переносное движение поступательное • угловая скорость вращения подвижной системы отсчета параллельна относительной скорости ω • относительная скорость точки равна нулю Модуль ускорения Кориолиса равен 2. 1. КИНЕМАТИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 1. ОПРЕДЕЛЕНИЕ ССС 40
1. 3. 5. Ускорение Кориолиса Это ускорение обращается в нуль, если Гюстав Гаспар Кориолис 1792 -1843 • угловая скорость подвижной системы отсчета равна нулю ω=0, т. е. переносное движение поступательное • угловая скорость вращения подвижной системы отсчета параллельна относительной скорости ω • относительная скорость точки равна нулю Модуль ускорения Кориолиса равен 2. 1. КИНЕМАТИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 1. ОПРЕДЕЛЕНИЕ ССС 40
 • 7, 8, 9
• 7, 8, 9
 1. 2. 4. Поступательное движение ТТ Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе • Очевидно, любое прямолинейное движение твердого тела является поступательным А В • Однако есть примеры поступательных движений, когда траектории С D отдельных его точек вовсе не являются прямыми линиями • Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 18
1. 2. 4. Поступательное движение ТТ Поступательным называется такое движение тела, при котором прямая, соединяющая две любые точки тела, остается в процессе движения параллельной самой себе • Очевидно, любое прямолинейное движение твердого тела является поступательным А В • Однако есть примеры поступательных движений, когда траектории С D отдельных его точек вовсе не являются прямыми линиями • Cпарник АВ при вращении кривошипов АС и BD также движется поступательно, он остается параллельным самому себе 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 18
 1. 2. 5. Теорема о кинематических характеристиках При поступательном движении твердого тела все его точки описывают конгруэнтные траектории и имеют в каждый момент времени одинаковые скорости и ускорения Доказательство • Для любых двух точек А и В z или O y x • Таким образом, траектория точки В получается из траектории точки А простым сдвигом на постоянный вектор , это и означает, что траектории конгруэнтны (при наложении совпадают) 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 19
1. 2. 5. Теорема о кинематических характеристиках При поступательном движении твердого тела все его точки описывают конгруэнтные траектории и имеют в каждый момент времени одинаковые скорости и ускорения Доказательство • Для любых двух точек А и В z или O y x • Таким образом, траектория точки В получается из траектории точки А простым сдвигом на постоянный вектор , это и означает, что траектории конгруэнтны (при наложении совпадают) 2. 1. ОПРЕДЕЛЕНИЕ ССС 1. КИНЕМАТИКА 19
 1. 2. 6. Вращательное движение ТТ z K • Положение твердого тела полностью опреде лится углом поворота φ этого тела вокруг оси A B(t) φ B(0) • Введем подвижную систему координат связанную с телом • Угол поворота φ тогда можно определить как угол, образуемый между осями в плоскости ху O x φ φ • При повороте тела на угол φ точка В y поворачивается вокруг оси также на этот угол • Закон движения произвольной точки тела определяется тогда уравнением Это уравнение называется законом вращательного движения твердого тела 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА 20
1. 2. 6. Вращательное движение ТТ z K • Положение твердого тела полностью опреде лится углом поворота φ этого тела вокруг оси A B(t) φ B(0) • Введем подвижную систему координат связанную с телом • Угол поворота φ тогда можно определить как угол, образуемый между осями в плоскости ху O x φ φ • При повороте тела на угол φ точка В y поворачивается вокруг оси также на этот угол • Закон движения произвольной точки тела определяется тогда уравнением Это уравнение называется законом вращательного движения твердого тела 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА 20
 1. 2. 7. Угловая скорость z K O • Закон движения имеет вид: A B(t) φ B(0) • За промежуток времени t тело повернется на угол φ φ • Переходя к пределу, получим мгновенную угловую скорость y x φ • Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту • Вектор угловой скорости ω направлен вдоль оси вращения в сторону, откуда это вращение видно происходящим против часовой стрелки 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА ТТ 21
1. 2. 7. Угловая скорость z K O • Закон движения имеет вид: A B(t) φ B(0) • За промежуток времени t тело повернется на угол φ φ • Переходя к пределу, получим мгновенную угловую скорость y x φ • Угловая скорость измеряется в радианах в секунду или числом оборотов в минуту • Вектор угловой скорости ω направлен вдоль оси вращения в сторону, откуда это вращение видно происходящим против часовой стрелки 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА ТТ 21
 1. 2. 10. Угловое ускорение • Если за промежуток времени t угловая скорость тела изменяется на ω, то можно ввести среднее угловое ускорение тела за время t • Переходя к пределу, получим мгновенное угловое ускорение • Размерность угловой скорости и углового ускорения: z A O O y x • Замедленное вращение x 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА y • Ускоренное вращение 22
1. 2. 10. Угловое ускорение • Если за промежуток времени t угловая скорость тела изменяется на ω, то можно ввести среднее угловое ускорение тела за время t • Переходя к пределу, получим мгновенное угловое ускорение • Размерность угловой скорости и углового ускорения: z A O O y x • Замедленное вращение x 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА y • Ускоренное вращение 22
 1. 2. 11. Скорость и ускорение точек ТТ Действительно, • Определим теперь ускорение точки В z A K O x – вращательное ускорение B – центростремительное ускорение y 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА 23
1. 2. 11. Скорость и ускорение точек ТТ Действительно, • Определим теперь ускорение точки В z A K O x – вращательное ускорение B – центростремительное ускорение y 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА 23
 2. 2. 12. Вращение относительно произвольной оси • В общем случае твердое тело может вращаться относительно оси , не сов падающей по направлению ни с одной из осей данной системы координат • Угловая скорость вращения тела вокруг оси z снова можно определить соотношением A но где O • Если lx=ly=0, то тело вращается вокруг оси Oz и, как мы установили, , где φ – угол поворота x тела вокруг этой оси • Аналогично, если ввести углы поворота тела φx, φy и относительно двух других осей, то y Т. о. , вращение тела относительно произвольной оси можно представить как суперпозицию вращений относительно трех осей неподвижной декартовой системы отсчета 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА ТТ 24
2. 2. 12. Вращение относительно произвольной оси • В общем случае твердое тело может вращаться относительно оси , не сов падающей по направлению ни с одной из осей данной системы координат • Угловая скорость вращения тела вокруг оси z снова можно определить соотношением A но где O • Если lx=ly=0, то тело вращается вокруг оси Oz и, как мы установили, , где φ – угол поворота x тела вокруг этой оси • Аналогично, если ввести углы поворота тела φx, φy и относительно двух других осей, то y Т. о. , вращение тела относительно произвольной оси можно представить как суперпозицию вращений относительно трех осей неподвижной декартовой системы отсчета 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЕКТОРНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ. 1. КИНЕМАТИКА ТТ 24
 10
10
 1. 3. 2. Определение и мотивация Движение твердого тела называется плоским (плоскопараллельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу 2. 1. КИНЕМАТИКА 1. ОПРЕДЕЛЕНИЕ ССС 28
1. 3. 2. Определение и мотивация Движение твердого тела называется плоским (плоскопараллельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу 2. 1. КИНЕМАТИКА 1. ОПРЕДЕЛЕНИЕ ССС 28
 1. 3. 3. Уравнение плоского движения y • Будем описывать движение сечения S относительно неподвижной системы координат Oxy, жестко связанной с плоскостью P S B А x O • Положение сечения относительно этой системы координат определяется положением какого либо принадлежащего ему отрезка AB • Т. о. , плоское движение ТТ слагается из поступательного движения вместе с полюсом и вращения вокруг полюса • Этим степеням свободы соответствует движение вдоль осей Оу и Ох и вращение относительно некоторой точки х1 y А φ B S O 1. КИНЕМАТИКА • Введем вспомогательную систему координат с у1 началом в точке А (полюсе) тела и осями , x , параллельными соответствующим осям неподвижной системы координат 29
1. 3. 3. Уравнение плоского движения y • Будем описывать движение сечения S относительно неподвижной системы координат Oxy, жестко связанной с плоскостью P S B А x O • Положение сечения относительно этой системы координат определяется положением какого либо принадлежащего ему отрезка AB • Т. о. , плоское движение ТТ слагается из поступательного движения вместе с полюсом и вращения вокруг полюса • Этим степеням свободы соответствует движение вдоль осей Оу и Ох и вращение относительно некоторой точки х1 y А φ B S O 1. КИНЕМАТИКА • Введем вспомогательную систему координат с у1 началом в точке А (полюсе) тела и осями , x , параллельными соответствующим осям неподвижной системы координат 29
 1. 3. 4. Теорема о скоростях точек ТТ х1 • Скорость произвольной точки М находится дифференцированием закона движения М y φ А O у1 x где введена скорость движения точки М относительно полюса А Скорость произвольной точки М ТТ, совершающего плоское движение, геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости этой точки в ее вращении вместе с телом вокруг полюса 1. КИНЕМАТИКА 30
1. 3. 4. Теорема о скоростях точек ТТ х1 • Скорость произвольной точки М находится дифференцированием закона движения М y φ А O у1 x где введена скорость движения точки М относительно полюса А Скорость произвольной точки М ТТ, совершающего плоское движение, геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости этой точки в ее вращении вместе с телом вокруг полюса 1. КИНЕМАТИКА 30
 1. 3. 5. Теорема о скоростях 2 -х точек Скорости произвольных двух точек связаны между собой Следствие 1 Проекции скоростей двух точек сечения S на прямую, их соединяющую, равны М А • Для доказательства достаточно спроеци ровать уравнение скоростей на прямую АМ и учесть, что Следствие 2 • Если точки А, В и С сечения S лежат на одной прямой, то концы векторов скоростей этих точек, тоже лежат на одной прямой, причем 1. КИНЕМАТИКА 31
1. 3. 5. Теорема о скоростях 2 -х точек Скорости произвольных двух точек связаны между собой Следствие 1 Проекции скоростей двух точек сечения S на прямую, их соединяющую, равны М А • Для доказательства достаточно спроеци ровать уравнение скоростей на прямую АМ и учесть, что Следствие 2 • Если точки А, В и С сечения S лежат на одной прямой, то концы векторов скоростей этих точек, тоже лежат на одной прямой, причем 1. КИНЕМАТИКА 31
 1. 3. 6. Теорема о МЦС Мгновенным центром скоростей (МЦС) сечения тела (или плоской фигуры) называется точка, скорость которой в данный момент времени равна нулю Теорема Если угловая скорость рассматриваемого сечения S в данный момент времени отлична от нуля, то мгновенный центр скоростей существует и единственен Действительно, рассмотрим сечение S • Пусть в некоторый момент времени t точки A и B имеют скорости, не параллельные другу • Это следует из теоремы о проекциях скоростей, так B как если бы скорость была отлична от нуля, то А S она одновременно должна была бы быть перпенди кулярна к АА’ и BB’. Последнее, однако, C невозможно в силу непараллельности скоростей точек А и В B’ А’ Теорема доказана 1. КИНЕМАТИКА 32
1. 3. 6. Теорема о МЦС Мгновенным центром скоростей (МЦС) сечения тела (или плоской фигуры) называется точка, скорость которой в данный момент времени равна нулю Теорема Если угловая скорость рассматриваемого сечения S в данный момент времени отлична от нуля, то мгновенный центр скоростей существует и единственен Действительно, рассмотрим сечение S • Пусть в некоторый момент времени t точки A и B имеют скорости, не параллельные другу • Это следует из теоремы о проекциях скоростей, так B как если бы скорость была отлична от нуля, то А S она одновременно должна была бы быть перпенди кулярна к АА’ и BB’. Последнее, однако, C невозможно в силу непараллельности скоростей точек А и В B’ А’ Теорема доказана 1. КИНЕМАТИКА 32
 1. 3. 7. Нахождение МЦС • МЦС может быть найден, если известны скорость одной точки тела, например A, и линия действия скорости второй точки тела, например, B A C ω • Восстановив перпендикуляры к вектору скорости точки A и к линии действия скорости точки B, находим точку их пересечения C, которая и будет МЦС • Вращение тела происходит туда, куда вектор скорости v. A первой точки поворачивает тело вокруг МЦС B • При определении скоростей точек тела плоское движение можно представить как последовательность мгновенных вращений вокруг мгновенного центра скоростей, который сам перемещается в плоскости движения тела 1. КИНЕМАТИКА 23
1. 3. 7. Нахождение МЦС • МЦС может быть найден, если известны скорость одной точки тела, например A, и линия действия скорости второй точки тела, например, B A C ω • Восстановив перпендикуляры к вектору скорости точки A и к линии действия скорости точки B, находим точку их пересечения C, которая и будет МЦС • Вращение тела происходит туда, куда вектор скорости v. A первой точки поворачивает тело вокруг МЦС B • При определении скоростей точек тела плоское движение можно представить как последовательность мгновенных вращений вокруг мгновенного центра скоростей, который сам перемещается в плоскости движения тела 1. КИНЕМАТИКА 23
 1. 3. 8. Теорема о сложении ускорений точек Ускорение любой точки тела, совершающего плоское движение, определяется как сумма ускорения полюса и ускорения данной Теорема о сложении ускорений точки во вращательном движении вокруг полюса Доказательство A B Теорема доказана 1. КИНЕМАТИКА 24
1. 3. 8. Теорема о сложении ускорений точек Ускорение любой точки тела, совершающего плоское движение, определяется как сумма ускорения полюса и ускорения данной Теорема о сложении ускорений точки во вращательном движении вокруг полюса Доказательство A B Теорема доказана 1. КИНЕМАТИКА 24
 Динамика 1
Динамика 1
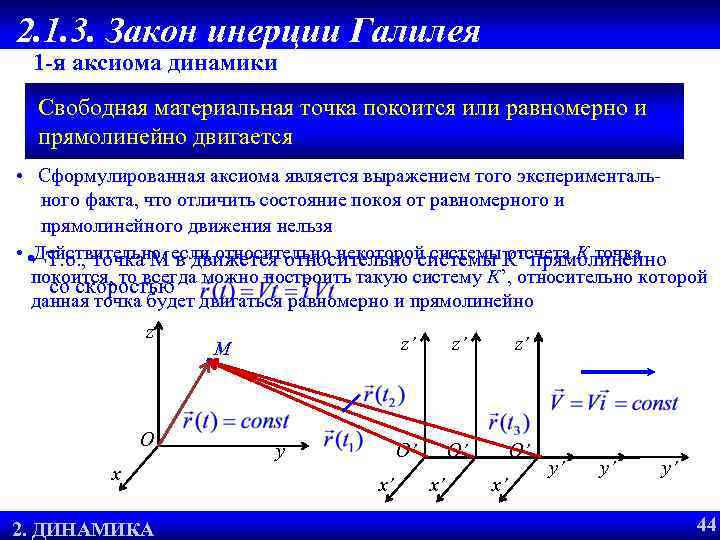 2. 1. 3. Закон инерции Галилея 1 -я аксиома динамики Свободная материальная точка покоится или равномерно и прямолинейно двигается • Сформулированная аксиома является выражением того эксперименталь ного факта, что отличить состояние покоя от равномерного и прямолинейного движения нельзя • Действительно, если относительно некоторой системы отсчета К точка • Т. о. , точка М в движется относительно системы К’ прямолинейно покоится, то всегда можно построить такую систему К’, относительно которой со скоростью данная точка будет двигаться равномерно и прямолинейно z О x 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ z’ y x’ z’ z’ О’ M О’ О’ x’ x’ y’ y’ y’ 44
2. 1. 3. Закон инерции Галилея 1 -я аксиома динамики Свободная материальная точка покоится или равномерно и прямолинейно двигается • Сформулированная аксиома является выражением того эксперименталь ного факта, что отличить состояние покоя от равномерного и прямолинейного движения нельзя • Действительно, если относительно некоторой системы отсчета К точка • Т. о. , точка М в движется относительно системы К’ прямолинейно покоится, то всегда можно построить такую систему К’, относительно которой со скоростью данная точка будет двигаться равномерно и прямолинейно z О x 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ z’ y x’ z’ z’ О’ M О’ О’ x’ x’ y’ y’ y’ 44
 Сила реакции опоры Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры Сила трения Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле: F=k*N где N сила реакции опоры , к коофициент трения Сила тяжести На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле F=mg где g ускорение свободного падения, m- масса тела
Сила реакции опоры Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры Сила трения Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле: F=k*N где N сила реакции опоры , к коофициент трения Сила тяжести На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле F=mg где g ускорение свободного падения, m- масса тела
 3
3
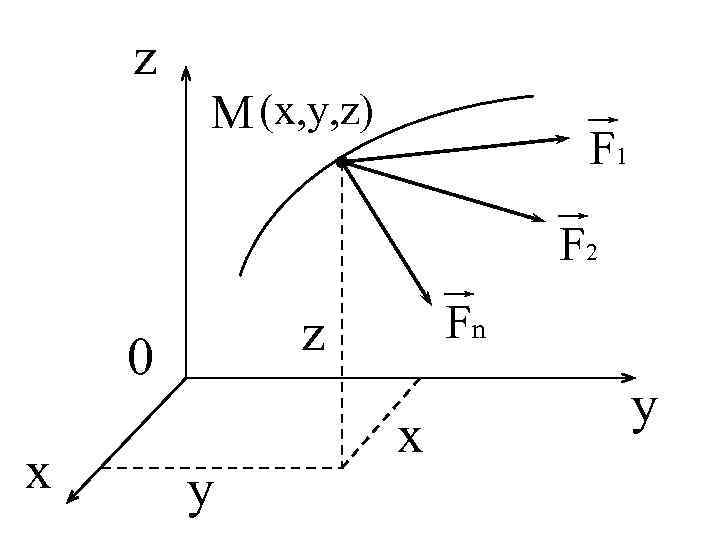
 Дифференциальные уравнения движения точки в декартовой системе координат.
Дифференциальные уравнения движения точки в декартовой системе координат.
 z M (x, y, z) F 1 F 2 0 x Fn z y x y
z M (x, y, z) F 1 F 2 0 x Fn z y x y
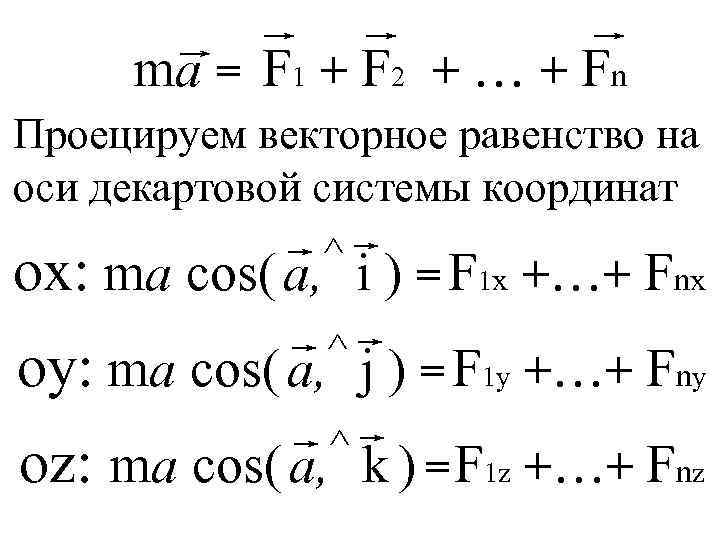 ma = F 1 + F 2 + … + Fn Проецируем векторное равенство на оси декартовой системы координат ^ ox: ma cos( a, i ) = 1 x +…+ Fnx F ^ oy: ma cos( a, j ) = 1 y +…+ Fny F ^ oz: ma cos( a, k ) = 1 z +…+ Fnz F
ma = F 1 + F 2 + … + Fn Проецируем векторное равенство на оси декартовой системы координат ^ ox: ma cos( a, i ) = 1 x +…+ Fnx F ^ oy: ma cos( a, j ) = 1 y +…+ Fny F ^ oz: ma cos( a, k ) = 1 z +…+ Fnz F
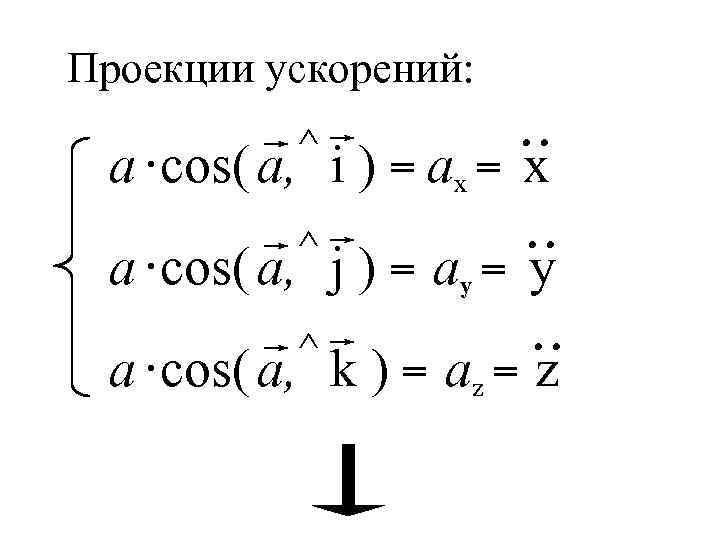 Проекции ускорений: ^ a ·cos( a, i ) = ax = x ^ a ·cos( a, j ) = ay = y ^ a ·cos( a, k ) = az = z
Проекции ускорений: ^ a ·cos( a, i ) = ax = x ^ a ·cos( a, j ) = ay = y ^ a ·cos( a, k ) = az = z
 дифференциальные уравнения движения точки в декартовой с. к. S Fkx m y = S Fky m z = S Fkz m x =
дифференциальные уравнения движения точки в декартовой с. к. S Fkx m y = S Fky m z = S Fkz m x =
 4
4
 Дифференциальные уравнения движения точки в осях естественного трехгранника.
Дифференциальные уравнения движения точки в осях естественного трехгранника.
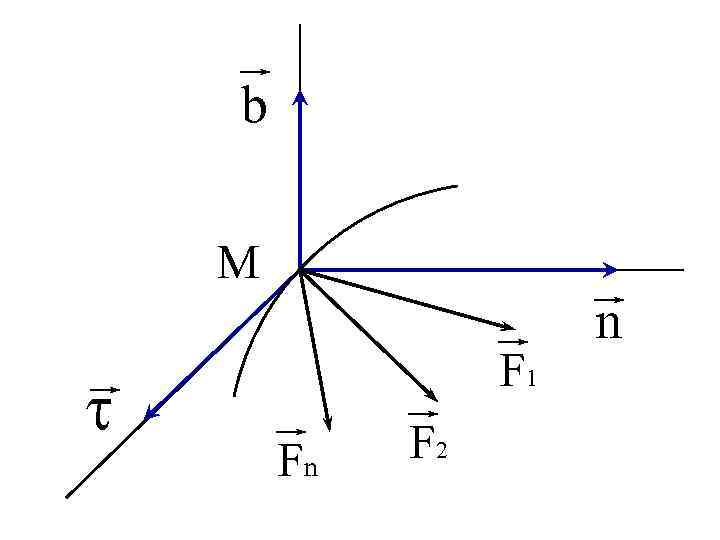 b M t F 1 Fn F 2 n
b M t F 1 Fn F 2 n
 - единичный вектор касательной n - единичный вектор главной нормали b - единичный вектор бинормали Запишем ІІ-ой закон Ньютона: ma = F 1 + F 2 + … + Fn
- единичный вектор касательной n - единичный вектор главной нормали b - единичный вектор бинормали Запишем ІІ-ой закон Ньютона: ma = F 1 + F 2 + … + Fn
 Проецируем это равенство на оси естественного трехгранника: ^ ma cos( a, t ) = F 1 cos(F 1, t ) + ^ ^ ^ ma cos( a, n ) = F 1 cos(F 1, n ) + ma cos( a, b ) = F 1 cos(F 1, b ) + . .
Проецируем это равенство на оси естественного трехгранника: ^ ma cos( a, t ) = F 1 cos(F 1, t ) + ^ ^ ^ ma cos( a, n ) = F 1 cos(F 1, n ) + ma cos( a, b ) = F 1 cos(F 1, b ) + . .
 Проекции ускорений будут равны: d. S a cos( a, t ) = 2 dt 2 V ^ a cos( a, n ) = 2 ^ ^ a cos( a, b ) = 0 - тангенсальная составляющая - нормальная составляющая - т. к. вектор ускорения лежит в соприкасающейся плоскости
Проекции ускорений будут равны: d. S a cos( a, t ) = 2 dt 2 V ^ a cos( a, n ) = 2 ^ ^ a cos( a, b ) = 0 - тангенсальная составляющая - нормальная составляющая - т. к. вектор ускорения лежит в соприкасающейся плоскости
 дифференциальные уравнения движения точки в осях естественного трехгранника d. S= m 2 dt 2 V = m 2 S Fk cos( Fk , t ) ^ S Fk cos( Fk , n ) ^
дифференциальные уравнения движения точки в осях естественного трехгранника d. S= m 2 dt 2 V = m 2 S Fk cos( Fk , t ) ^ S Fk cos( Fk , n ) ^
 5
5
 Прямая задача По известной массе, известному закону движения требуется определить результирующую силу, действующую на тело.
Прямая задача По известной массе, известному закону движения требуется определить результирующую силу, действующую на тело.
 Дано: m x = x(t) y = y(t) z = z(t) Найти: F - ?
Дано: m x = x(t) y = y(t) z = z(t) Найти: F - ?
 Решение: m x = Fx m y = Fy m z = Fz F = Fx + Fy + Fz - модуль силы 2 2 2
Решение: m x = Fx m y = Fy m z = Fz F = Fx + Fy + Fz - модуль силы 2 2 2
 Направление задается направляющими косинусами: Fx cos(F, x ) = F Fy ^ cos(F, y ) = F Fz ^ cos(F, z ) = F ^
Направление задается направляющими косинусами: Fx cos(F, x ) = F Fy ^ cos(F, y ) = F Fz ^ cos(F, z ) = F ^
 Обратная задача По известной массе, известным силам, известным начальным условиям требуется определить закон движения.
Обратная задача По известной массе, известным силам, известным начальным условиям требуется определить закон движения.
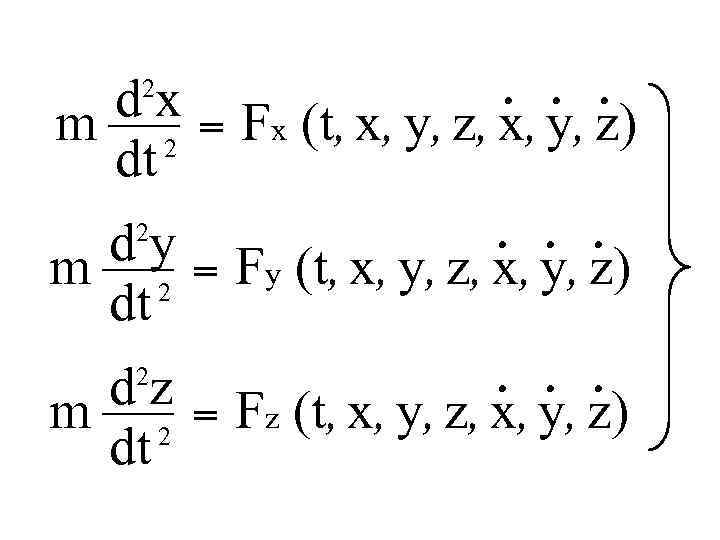 d x = Fx (t, x, y, z) m 2 dt 2 d y = Fy (t, x, y, z) m 2 dt 2 d z = Fz (t, x, y, z) m 2 dt 2
d x = Fx (t, x, y, z) m 2 dt 2 d y = Fy (t, x, y, z) m 2 dt 2 d z = Fz (t, x, y, z) m 2 dt 2
 Для того, чтобы получить закон движения, необходимо дважды проинтегрировать каждое уравнение, используя начальные условия (но не всякий интеграл берется).
Для того, чтобы получить закон движения, необходимо дважды проинтегрировать каждое уравнение, используя начальные условия (но не всякий интеграл берется).
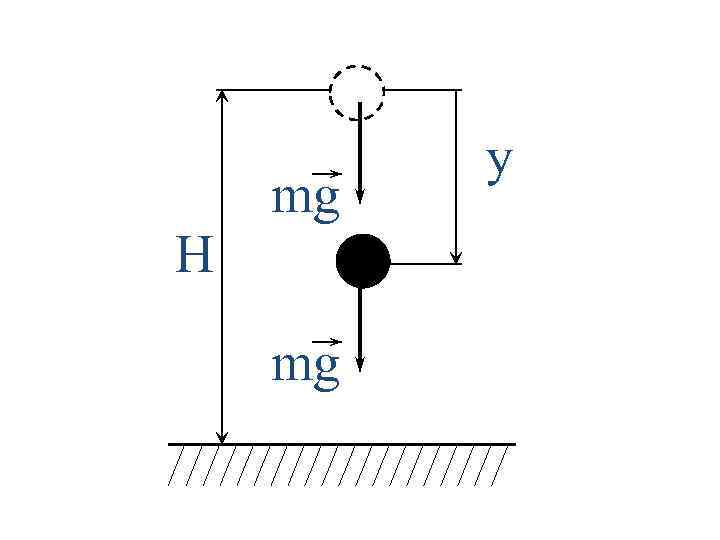 mg H mg y
mg H mg y
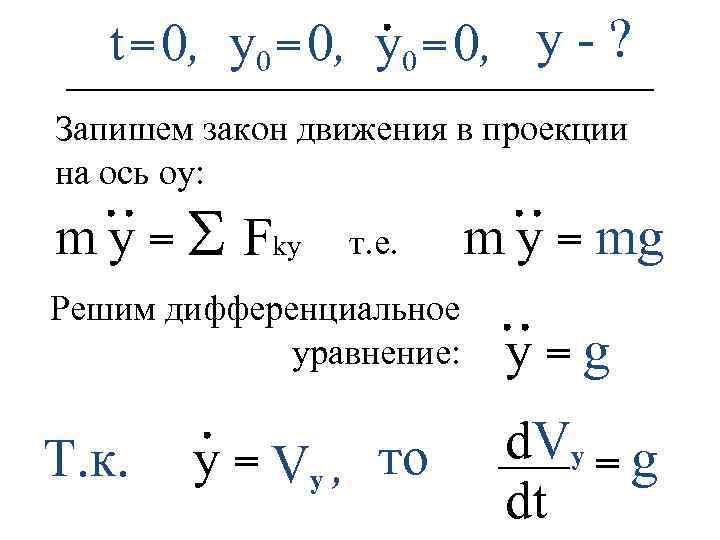 t = 0, y 0 = 0, y - ? Запишем закон движения в проекции на ось оу: m y = S Fky т. е. m y = mg Решим дифференциальное уравнение: Т. к. y = Vy , то y = g d. Vy = g dt
t = 0, y 0 = 0, y - ? Запишем закон движения в проекции на ось оу: m y = S Fky т. е. m y = mg Решим дифференциальное уравнение: Т. к. y = Vy , то y = g d. Vy = g dt
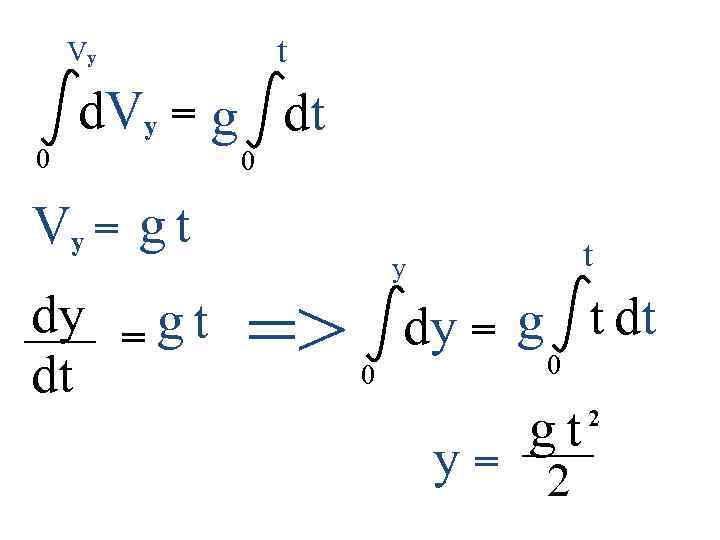 t Vy d. Vy = g dt 0 0 Vy = g t dt => t y dy = g t dt 0 0 g t y = 2 2
t Vy d. Vy = g dt 0 0 Vy = g t dt => t y dy = g t dt 0 0 g t y = 2 2
 6
6
 2. 1. 16. Криволинейное движение Тело массы m брошено под углом α к горизонту с начальной скоростью v 0. Пренебрегая сопротивлением среды и считая дальность полета и высоту над горизонтом малыми по сравнению с радиусом Земли, найти закон движения, траекторию, дальность и время полета, а также высоту траектории. у v 0 • Выберем систему координат Мху α х М • Единственной силой, действую щей на точку является сила тяжести • Уравнение Ньютона в проекциях на оси координат имеет вид НУ: • Исключая из полученных уравнений движения время , получим уравнение траектории 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ 57
2. 1. 16. Криволинейное движение Тело массы m брошено под углом α к горизонту с начальной скоростью v 0. Пренебрегая сопротивлением среды и считая дальность полета и высоту над горизонтом малыми по сравнению с радиусом Земли, найти закон движения, траекторию, дальность и время полета, а также высоту траектории. у v 0 • Выберем систему координат Мху α х М • Единственной силой, действую щей на точку является сила тяжести • Уравнение Ньютона в проекциях на оси координат имеет вид НУ: • Исключая из полученных уравнений движения время , получим уравнение траектории 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ 57
 2. 1. 16. Криволинейное движение у v 0 α М х • Траектория полета – парабола • Дальность полета определим, полагая в уравнении траектории у =0 • Высоту H траектории получим, полагая в уравнении траектории x = L/2 • Время полета 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ 58
2. 1. 16. Криволинейное движение у v 0 α М х • Траектория полета – парабола • Дальность полета определим, полагая в уравнении траектории у =0 • Высоту H траектории получим, полагая в уравнении траектории x = L/2 • Время полета 2. 1. ДИНАМИКА ССС 2. ОПРЕДЕЛЕНИЕ 58
 7, 8
7, 8
 Свободное падение тела с учетом сопротивления среды. При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления. Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, где определяется свойствами среды и формой тела. Свободное падение тела без учета сопротивления среды Рассмотрим движение тела М, падающего на поверхность Земли с высоты Н, полагая вес тела G постоянным. Пренебрегая размерами тела, будем считать его материальной точкой. Сначала рассмотрим падение тела в пустоте, т. е. без учета сопротивления воздуха. n. Направим ось у по траектории прямолинейного движения тела в сторону его движения и примем за начало координат начальное положение тела. Если начальная скорость тела равна нулю, то начальные условия рассматриваемого движения будут иметь вид
Свободное падение тела с учетом сопротивления среды. При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления. Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, где определяется свойствами среды и формой тела. Свободное падение тела без учета сопротивления среды Рассмотрим движение тела М, падающего на поверхность Земли с высоты Н, полагая вес тела G постоянным. Пренебрегая размерами тела, будем считать его материальной точкой. Сначала рассмотрим падение тела в пустоте, т. е. без учета сопротивления воздуха. n. Направим ось у по траектории прямолинейного движения тела в сторону его движения и примем за начало координат начальное положение тела. Если начальная скорость тела равна нулю, то начальные условия рассматриваемого движения будут иметь вид
 9
9
 ТЕОРЕМА ИМПУЛЬСОВ ДЛЯ СИСТЕМЫ, ВЫРАЖЕННАЯ ЧЕРЕЗ ДВИЖЕНИЕ ЦЕНТРА МАСС. Изменение скорости центра масс системы за конечный промежуток времени равно импульсу внешних сил системы за тот же промежуток времени, деленному на массу всей системы. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 1. Для точки: изменение кинетической энергии точки на конечном ее перемещении равно работе приложенных к ней активных сил (касательные составляющие реакций неидеальных связей включаются в число активных сил): Для случая относительного движения: изменение кинетической энергии точки при относительном движении равно работе приложенных к ней активных сил и переносной силы инерции (см. "Частные случаи интегрирования"): 2. Для системы: изменение кинетической энергии системы на некотором перемещении ее точек равно работе приложенных к ней внешних активных сил и внутренних сил, приложенных к точкам системы, расстояние между которыми меняется: Если система неизменяема (твердое тело), то ΣAi=0 и изменение кинетической энергии равно работе только внешних активных сил. ТЕОРЕМА ИМПУЛЬСОВ (теорема количества движения в конечной форме). 1. Для точки: изменение количества движения точки за конечный промежуток времени равно сумме импульсов, приложенных к точке сил (или импульсу равнодействующей приложенных к точке сил) или в координатной форме: 2. Для системы: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил: или в координатной форме: Следствия: при отсутствии внешних сил количество движения системы есть величина постоянная; если внешние силы системы перпендикулярны некоторой оси, то проекция количества движения на эту ось есть величина постоянная.
ТЕОРЕМА ИМПУЛЬСОВ ДЛЯ СИСТЕМЫ, ВЫРАЖЕННАЯ ЧЕРЕЗ ДВИЖЕНИЕ ЦЕНТРА МАСС. Изменение скорости центра масс системы за конечный промежуток времени равно импульсу внешних сил системы за тот же промежуток времени, деленному на массу всей системы. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 1. Для точки: изменение кинетической энергии точки на конечном ее перемещении равно работе приложенных к ней активных сил (касательные составляющие реакций неидеальных связей включаются в число активных сил): Для случая относительного движения: изменение кинетической энергии точки при относительном движении равно работе приложенных к ней активных сил и переносной силы инерции (см. "Частные случаи интегрирования"): 2. Для системы: изменение кинетической энергии системы на некотором перемещении ее точек равно работе приложенных к ней внешних активных сил и внутренних сил, приложенных к точкам системы, расстояние между которыми меняется: Если система неизменяема (твердое тело), то ΣAi=0 и изменение кинетической энергии равно работе только внешних активных сил. ТЕОРЕМА ИМПУЛЬСОВ (теорема количества движения в конечной форме). 1. Для точки: изменение количества движения точки за конечный промежуток времени равно сумме импульсов, приложенных к точке сил (или импульсу равнодействующей приложенных к точке сил) или в координатной форме: 2. Для системы: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил: или в координатной форме: Следствия: при отсутствии внешних сил количество движения системы есть величина постоянная; если внешние силы системы перпендикулярны некоторой оси, то проекция количества движения на эту ось есть величина постоянная.
 11
11
 12, 13, 14
12, 13, 14
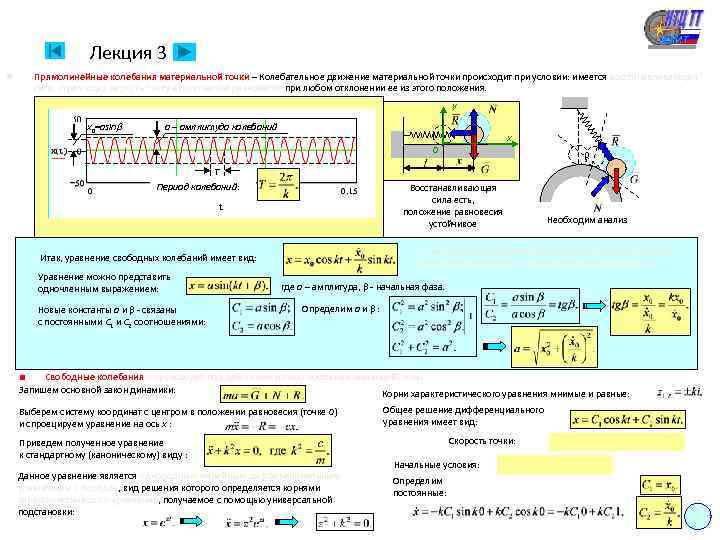 Лекция 3 Прямолинейные колебания материальной точки – Колебательное движение материальной точки происходит при условии: имеется восстанавливающая сила, стремящая вернуть точку в положение равновесия при любом отклонении ее из этого положения. n y x 0=asin a – амллитуда колебаний x O Восстанавливающая сила есть, положение равновесия устойчивое T Период колебаний: Восстанавливающей силы нет, положение равновесия неустойчивое Восстанавливающей силы нет, положение равновесия безразличное Восстанавливающая сила есть, положение равновесия устойчивое Необходим анализ Сила упругости пружины – пример линейной восстанавливающей силы. Направлена всегда к положению равновесия, величина прямо пропорциональна линейному Причиной возникновения свободных колебаний является Итак, уравнение свободных колебаний имеет вид: удлинению (укорочению) пружины, равному отклонению тела от положения равновесия: начальное смещение x 0 и/или начальная скорость v 0. Уравнение можно представить с – коэффициент жесткости пружины, численно равный силе, под действием которой пружина изменяет свою длину на единицу, измеряется в Н/м в где a – амплитуда, - начальная фаза. одночленным выражением: системе СИ. Определим a и : Новые константы a и - связаны точки: Виды колебаний материальной с постоянными Cколебания (без учета сопротивления среды). n 1. Свободные 1 и C 2 соотношениями: n 2. Свободные колебания с учетом сопротивления среды (затухающие колебания). n 3. Вынужденные колебания. n 4. Вынужденные колебания с учетом сопротивления среды. ■ Свободные колебания – происходят под действием только восстанавливающей силы. Запишем основной закон динамики: Корни характеристического уравнения мнимые и равные: n Выберем систему координат с центром в положении равновесия (точке O) и спроецируем уравнение на ось x : Приведем полученное уравнение к стандартному (каноническому) виду : Данное уравнение является однородным линейным дифференциальным уравнением II порядка, вид решения которого определяется корнями характеристического уравнения, получаемое с помощью универсальной подстановки: Общее решение дифференциального уравнения имеет вид: Скорость точки: Начальные условия: Определим постоянные: 9
Лекция 3 Прямолинейные колебания материальной точки – Колебательное движение материальной точки происходит при условии: имеется восстанавливающая сила, стремящая вернуть точку в положение равновесия при любом отклонении ее из этого положения. n y x 0=asin a – амллитуда колебаний x O Восстанавливающая сила есть, положение равновесия устойчивое T Период колебаний: Восстанавливающей силы нет, положение равновесия неустойчивое Восстанавливающей силы нет, положение равновесия безразличное Восстанавливающая сила есть, положение равновесия устойчивое Необходим анализ Сила упругости пружины – пример линейной восстанавливающей силы. Направлена всегда к положению равновесия, величина прямо пропорциональна линейному Причиной возникновения свободных колебаний является Итак, уравнение свободных колебаний имеет вид: удлинению (укорочению) пружины, равному отклонению тела от положения равновесия: начальное смещение x 0 и/или начальная скорость v 0. Уравнение можно представить с – коэффициент жесткости пружины, численно равный силе, под действием которой пружина изменяет свою длину на единицу, измеряется в Н/м в где a – амплитуда, - начальная фаза. одночленным выражением: системе СИ. Определим a и : Новые константы a и - связаны точки: Виды колебаний материальной с постоянными Cколебания (без учета сопротивления среды). n 1. Свободные 1 и C 2 соотношениями: n 2. Свободные колебания с учетом сопротивления среды (затухающие колебания). n 3. Вынужденные колебания. n 4. Вынужденные колебания с учетом сопротивления среды. ■ Свободные колебания – происходят под действием только восстанавливающей силы. Запишем основной закон динамики: Корни характеристического уравнения мнимые и равные: n Выберем систему координат с центром в положении равновесия (точке O) и спроецируем уравнение на ось x : Приведем полученное уравнение к стандартному (каноническому) виду : Данное уравнение является однородным линейным дифференциальным уравнением II порядка, вид решения которого определяется корнями характеристического уравнения, получаемое с помощью универсальной подстановки: Общее решение дифференциального уравнения имеет вид: Скорость точки: Начальные условия: Определим постоянные: 9
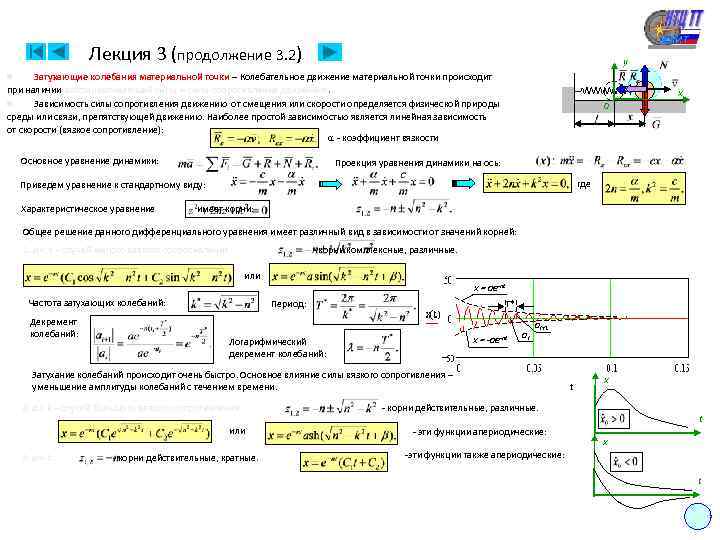 Лекция 3 (продолжение 3. 2) y Затухающие колебания материальной точки – Колебательное движение материальной точки происходит при наличии восстанавливающей силы и силы сопротивления движению. n Зависимость силы сопротивления движению от смещения или скорости определяется физической природы среды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимость от скорости (вязкое сопротивление): - коэффициент вязкости n Основное уравнение динамики: x O Проекция уравнения динамики на ось: где Приведем уравнение к стандартному виду: Характеристическое уравнение имеет корни: Общее решение данного дифференциального уравнения имеет различный вид в зависимости от значений корней: 1. n < k – случай малого вязкого сопротивления: - корни комплексные, различные. или Частота затухающих колебаний: Декремент колебаний: x = ae-nt Период: T* x = -ae-nt Логарифмический декремент колебаний: ai ai+1 Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n > k – случай большого вязкого сопротивления: или 3. n = k : - корни действительные, кратные. x - корни действительные, различные. - эти функции апериодические: t x -эти функции также апериодические: t 10
Лекция 3 (продолжение 3. 2) y Затухающие колебания материальной точки – Колебательное движение материальной точки происходит при наличии восстанавливающей силы и силы сопротивления движению. n Зависимость силы сопротивления движению от смещения или скорости определяется физической природы среды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимость от скорости (вязкое сопротивление): - коэффициент вязкости n Основное уравнение динамики: x O Проекция уравнения динамики на ось: где Приведем уравнение к стандартному виду: Характеристическое уравнение имеет корни: Общее решение данного дифференциального уравнения имеет различный вид в зависимости от значений корней: 1. n < k – случай малого вязкого сопротивления: - корни комплексные, различные. или Частота затухающих колебаний: Декремент колебаний: x = ae-nt Период: T* x = -ae-nt Логарифмический декремент колебаний: ai ai+1 Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n > k – случай большого вязкого сопротивления: или 3. n = k : - корни действительные, кратные. x - корни действительные, различные. - эти функции апериодические: t x -эти функции также апериодические: t 10
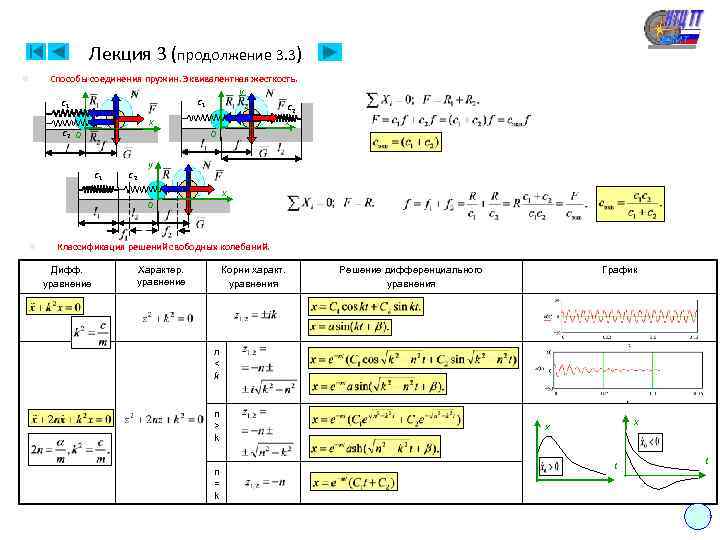 Лекция 3 (продолжение 3. 3) Способы соединения пружин. Эквивалентная жесткость. y y с1 с1 с2 x x с2 O O n с1 с2 y x O n Классификация решений свободных колебаний. Дифф. уравнение Характер. уравнение Корни характ. уравнения Решение дифференциального уравнения График n < k n > k n = k x x t t 11
Лекция 3 (продолжение 3. 3) Способы соединения пружин. Эквивалентная жесткость. y y с1 с1 с2 x x с2 O O n с1 с2 y x O n Классификация решений свободных колебаний. Дифф. уравнение Характер. уравнение Корни характ. уравнения Решение дифференциального уравнения График n < k n > k n = k x x t t 11
 Лекция 4 n n Вынужденные колебания материальной точки – Наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой. Возмущающая сила может иметь различную природу. Например, в частном случае инерционное воздействие неуравновешенной массы m 1 вращающегося ротора вызывает гармонически изменяющиеся проекции силы: y Основное уравнение динамики: y Проекция уравнения x динамики на ось: A x O Приведем уравнение O к стандартному виду: Решение этого неоднородного дифференциального уравнения состоит их двух частей x = x 1 + x 2 : x 1 – общее решение соответствующего однородного уравнения и x 2 – частное решение неоднородного уравнения: Общее решение: Частное решение подбираем в форме правой части: Полученное равенство должно удовлетворяться при любом t. Тогда: или В итоге полное решение: Таким образом, частное решение: или Постоянные С 1 и С 2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат сложения (наложения) свободных (x 1) и вынужденных (x 2) колебаний. 1. Если p < k (вынужденные колебания малой частоты), 2. Если p > k (вынужденные колебания большой частоты), то фаза колебаний совпадает с фазой возмущающей силы: то фаза колебаний противоположна фазе возмущающей силы: 12
Лекция 4 n n Вынужденные колебания материальной точки – Наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой. Возмущающая сила может иметь различную природу. Например, в частном случае инерционное воздействие неуравновешенной массы m 1 вращающегося ротора вызывает гармонически изменяющиеся проекции силы: y Основное уравнение динамики: y Проекция уравнения x динамики на ось: A x O Приведем уравнение O к стандартному виду: Решение этого неоднородного дифференциального уравнения состоит их двух частей x = x 1 + x 2 : x 1 – общее решение соответствующего однородного уравнения и x 2 – частное решение неоднородного уравнения: Общее решение: Частное решение подбираем в форме правой части: Полученное равенство должно удовлетворяться при любом t. Тогда: или В итоге полное решение: Таким образом, частное решение: или Постоянные С 1 и С 2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат сложения (наложения) свободных (x 1) и вынужденных (x 2) колебаний. 1. Если p < k (вынужденные колебания малой частоты), 2. Если p > k (вынужденные колебания большой частоты), то фаза колебаний совпадает с фазой возмущающей силы: то фаза колебаний противоположна фазе возмущающей силы: 12
 Лекция 4 (продолжение 4. 2) Коэффициент динамичности – отношение амплитуды вынужденных колебаний к статическому отклонению точки под действием постоянной силы H = const: Амплитуда вынужденных колебаний: Таким образом, при p < k (малая частота вынужденных колебаний) коэффициент динамичности: Статическое отклонение можно найти из уравнения равновесия: Здесь: При p > k (большая частота вынужденных колебаний) коэффициент динамичности: Отсюда: 3 2 Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). 1 Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. 0 3 1 2 Дифференциальное уравнение колебаний при равенстве частот: Приравнивая коэффициенты при одинаковых Делением второго уравнения Общее решение: Частное взять нельзя, т. к. получится тригонометрических функциях получаем систему уравнений: решение в форме правой части на первое получаем сдвиг фазы линейно зависимое решение (см. общее вынужденных колебаний: Возьмем частное решение в виде и вычислим производные : решение). Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление): Подставим в дифференциальное уравнение: Возведением в степень обоих Вынужденные колебания при сопротивлении движению не затухают. Частота и период уравнений и сложением их Таким образом, получено решение: или вынужденных колебаний равны частоте и периоду изменения получаем амплитуду возмущающей силы. Коэффициент динамичности при резонансе имеет вынужденных колебаний: конечную величину и зависит от соотношения n и к. Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени. Влияние сопротивления движению при вынужденных колебаниях. Дифференциальное уравнение при наличии вязкого сопротивления имеет вид: Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть). Частное решение возьмем в виде и вычислим производные : Подставим в дифференциальное уравнение: 13
Лекция 4 (продолжение 4. 2) Коэффициент динамичности – отношение амплитуды вынужденных колебаний к статическому отклонению точки под действием постоянной силы H = const: Амплитуда вынужденных колебаний: Таким образом, при p < k (малая частота вынужденных колебаний) коэффициент динамичности: Статическое отклонение можно найти из уравнения равновесия: Здесь: При p > k (большая частота вынужденных колебаний) коэффициент динамичности: Отсюда: 3 2 Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). 1 Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. 0 3 1 2 Дифференциальное уравнение колебаний при равенстве частот: Приравнивая коэффициенты при одинаковых Делением второго уравнения Общее решение: Частное взять нельзя, т. к. получится тригонометрических функциях получаем систему уравнений: решение в форме правой части на первое получаем сдвиг фазы линейно зависимое решение (см. общее вынужденных колебаний: Возьмем частное решение в виде и вычислим производные : решение). Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление): Подставим в дифференциальное уравнение: Возведением в степень обоих Вынужденные колебания при сопротивлении движению не затухают. Частота и период уравнений и сложением их Таким образом, получено решение: или вынужденных колебаний равны частоте и периоду изменения получаем амплитуду возмущающей силы. Коэффициент динамичности при резонансе имеет вынужденных колебаний: конечную величину и зависит от соотношения n и к. Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени. Влияние сопротивления движению при вынужденных колебаниях. Дифференциальное уравнение при наличии вязкого сопротивления имеет вид: Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть). Частное решение возьмем в виде и вычислим производные : Подставим в дифференциальное уравнение: 13
 15
15
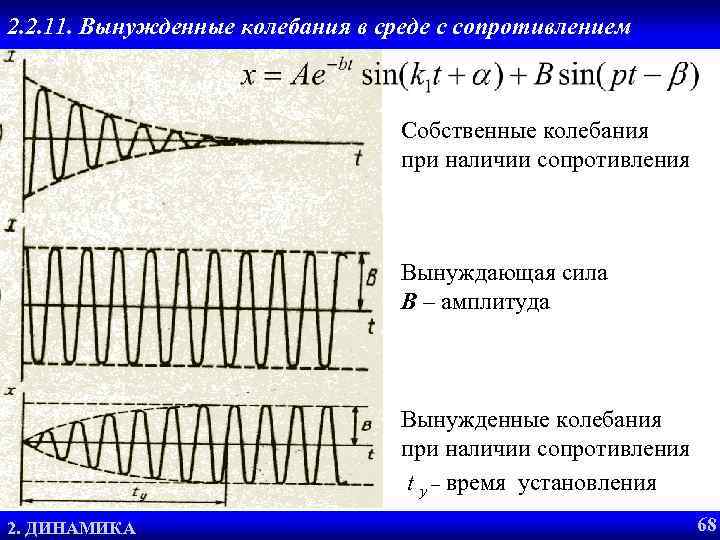 График вынужденных колебанийс сопротивлением 2. 2. 11. Вынужденные колебания в среде Собственные колебания при наличии сопротивления Вынуждающая сила B – амплитуда Вынужденные колебания при наличии сопротивления t у – время установления 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 2 2. ДИНАМИКА 68
График вынужденных колебанийс сопротивлением 2. 2. 11. Вынужденные колебания в среде Собственные колебания при наличии сопротивления Вынуждающая сила B – амплитуда Вынужденные колебания при наличии сопротивления t у – время установления 2. 1. ОПРЕДЕЛЕНИЕ ССС ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 2 2. ДИНАМИКА 68
 16
16
 Лекция 4 (продолжение 4. 2) Коэффициент динамичности – отношение амплитуды вынужденных колебаний к статическому отклонению точки под действием постоянной силы H = const: Амплитуда вынужденных колебаний: Таким образом, при p < k (малая частота вынужденных колебаний) коэффициент динамичности: Статическое отклонение можно найти из уравнения равновесия: Здесь: При p > k (большая частота вынужденных колебаний) коэффициент динамичности: Отсюда: 3 2 Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). 1 Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. 0 3 1 2 Дифференциальное уравнение колебаний при равенстве частот: Приравнивая коэффициенты при одинаковых Делением второго уравнения Общее решение: Частное взять нельзя, т. к. получится тригонометрических функциях получаем систему уравнений: решение в форме правой части на первое получаем сдвиг фазы линейно зависимое решение (см. общее вынужденных колебаний: Возьмем частное решение в виде и вычислим производные : решение). Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление): Подставим в дифференциальное уравнение: Возведением в степень обоих Вынужденные колебания при сопротивлении движению не затухают. Частота и период уравнений и сложением их Таким образом, получено решение: или вынужденных колебаний равны частоте и периоду изменения получаем амплитуду возмущающей силы. Коэффициент динамичности при резонансе имеет вынужденных колебаний: конечную величину и зависит от соотношения n и к. Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени. Влияние сопротивления движению при вынужденных колебаниях. Дифференциальное уравнение при наличии вязкого сопротивления имеет вид: Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть). Частное решение возьмем в виде и вычислим производные : Подставим в дифференциальное уравнение: 13
Лекция 4 (продолжение 4. 2) Коэффициент динамичности – отношение амплитуды вынужденных колебаний к статическому отклонению точки под действием постоянной силы H = const: Амплитуда вынужденных колебаний: Таким образом, при p < k (малая частота вынужденных колебаний) коэффициент динамичности: Статическое отклонение можно найти из уравнения равновесия: Здесь: При p > k (большая частота вынужденных колебаний) коэффициент динамичности: Отсюда: 3 2 Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). 1 Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. 0 3 1 2 Дифференциальное уравнение колебаний при равенстве частот: Приравнивая коэффициенты при одинаковых Делением второго уравнения Общее решение: Частное взять нельзя, т. к. получится тригонометрических функциях получаем систему уравнений: решение в форме правой части на первое получаем сдвиг фазы линейно зависимое решение (см. общее вынужденных колебаний: Возьмем частное решение в виде и вычислим производные : решение). Таким образом, уравнение движения при вынужденных колебаний с учетом сопротивления движению, например при n < k (малое сопротивление): Подставим в дифференциальное уравнение: Возведением в степень обоих Вынужденные колебания при сопротивлении движению не затухают. Частота и период уравнений и сложением их Таким образом, получено решение: или вынужденных колебаний равны частоте и периоду изменения получаем амплитуду возмущающей силы. Коэффициент динамичности при резонансе имеет вынужденных колебаний: конечную величину и зависит от соотношения n и к. Вынужденные колебания при резонансе имеют амплитуду неограниченно возрастающую пропорционально времени. Влияние сопротивления движению при вынужденных колебаниях. Дифференциальное уравнение при наличии вязкого сопротивления имеет вид: Общее решение выбирается из таблицы (Лекция 3, стр. 11) в зависимости от соотношения n и к (посмотреть). Частное решение возьмем в виде и вычислим производные : Подставим в дифференциальное уравнение: 13
 17
17
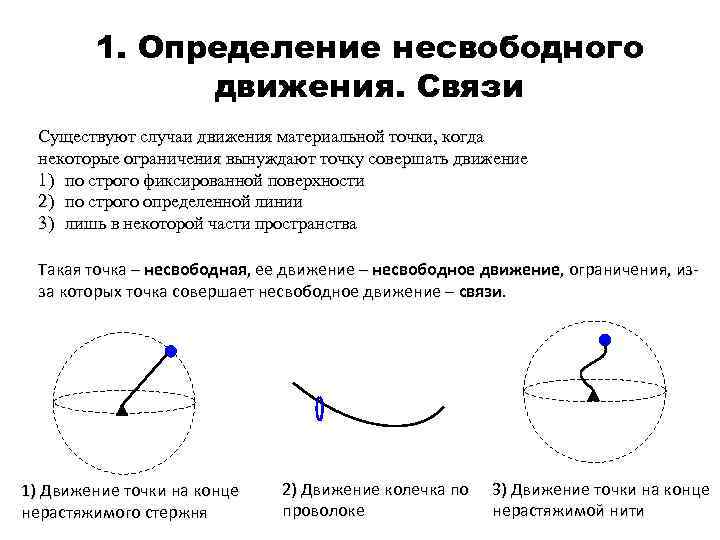 1. Определение несвободного движения. Связи Существуют случаи движения материальной точки, когда некоторые ограничения вынуждают точку совершать движение 1) по строго фиксированной поверхности 2) по строго определенной линии 3) лишь в некоторой части пространства Такая точка – несвободная, ее движение – несвободное движение, ограничения, изза которых точка совершает несвободное движение – связи. 1) Движение точки на конце нерастяжимого стержня 2) Движение колечка по проволоке 3) Движение точки на конце нерастяжимой нити
1. Определение несвободного движения. Связи Существуют случаи движения материальной точки, когда некоторые ограничения вынуждают точку совершать движение 1) по строго фиксированной поверхности 2) по строго определенной линии 3) лишь в некоторой части пространства Такая точка – несвободная, ее движение – несвободное движение, ограничения, изза которых точка совершает несвободное движение – связи. 1) Движение точки на конце нерастяжимого стержня 2) Движение колечка по проволоке 3) Движение точки на конце нерастяжимой нити
 2. Принцип освобождаемости При рассмотрении несвободного движения следует действие связей на материальную точку заменить реакциями этих связей и рассматривать материальную точку как свободную, но находящуюся под действием как сил активных, так и реакций связей. Основное уравнение динамики активные реакции В общем случае реакция связи заранее не известна и должна определяться в ходе решения задачи Основное уравнение динамики позволяет непосредственно решать такие задачи, когда заданы движение и активные силы и требуется определить реакции
2. Принцип освобождаемости При рассмотрении несвободного движения следует действие связей на материальную точку заменить реакциями этих связей и рассматривать материальную точку как свободную, но находящуюся под действием как сил активных, так и реакций связей. Основное уравнение динамики активные реакции В общем случае реакция связи заранее не известна и должна определяться в ходе решения задачи Основное уравнение динамики позволяет непосредственно решать такие задачи, когда заданы движение и активные силы и требуется определить реакции
 18 время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта; пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта. Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона. Основное уравнение динамики относительного движения материальной точки имеет вид: где m — масса тела, — ускорение тела относительно неинерциальной системы отсчёта, — сумма всех внешних сил, действующих на тело, — переносное ускорение тела, — кориолисово ускорение тела. Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции: — переносная сила инерции — сила Кориолиса
18 время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта; пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта. Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона. Основное уравнение динамики относительного движения материальной точки имеет вид: где m — масса тела, — ускорение тела относительно неинерциальной системы отсчёта, — сумма всех внешних сил, действующих на тело, — переносное ускорение тела, — кориолисово ускорение тела. Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции: — переносная сила инерции — сила Кориолиса
 19
19
 20
20
 Внешние силы F e - силы, действующие на тела данной системы со стороны тел, не входящих в данную систему Внутренние силы F i - силы взаимодействия между телами данной системы.
Внешние силы F e - силы, действующие на тела данной системы со стороны тел, не входящих в данную систему Внутренние силы F i - силы взаимодействия между телами данной системы.
 Главный вектор внутренних сил системы равен нулю. Главный момент внутренних сил системы равен нулю.
Главный вектор внутренних сил системы равен нулю. Главный момент внутренних сил системы равен нулю.
 21
21
 2. 4. 4. Центр масс • Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса • Так как механическая система состоит из N материальных точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек Центром масс механической системы или центром инерции относительно некоторой декартовой системы координат называется точка с координатами 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 78
2. 4. 4. Центр масс • Важнейшей динамической характеристикой материальной точки, определяющей ее способность сохранять движение, является масса • Так как механическая система состоит из N материальных точек с массой mi, то можно ввести массу всей системы, равную сумме масс ее точек Центром масс механической системы или центром инерции относительно некоторой декартовой системы координат называется точка с координатами 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 78
 2. 3. 5. Координаты ЦМ твердого тела • Если плотность распределения массы равна , то • Координаты центра масс равны • Переходя к пределу 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ , имеем 79
2. 3. 5. Координаты ЦМ твердого тела • Если плотность распределения массы равна , то • Координаты центра масс равны • Переходя к пределу 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ , имеем 79
 22
22
 2. 4. 6. Момент инерции относительно оси Моментом инерции тела (системы) относительно данной оси Oz называется величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний hi до этой оси z hiz Но mi y O x xi yi Аналогично определяются моменты инерции системы относительно осей Ox и Oy 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 80
2. 4. 6. Момент инерции относительно оси Моментом инерции тела (системы) относительно данной оси Oz называется величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний hi до этой оси z hiz Но mi y O x xi yi Аналогично определяются моменты инерции системы относительно осей Ox и Oy 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 80
 2. 4. 7. Момент инерции относительно центра Моментом инерции тела (системы) относительно центра O называется скалярная величина, равная сумме произведений массы каждой точки тела (системы) на квадрат ее расстояния до этого центра z hiz mi y O x xi yi Моменты инерции точки относительно осей Ox, Oy, Oz равны 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 91
2. 4. 7. Момент инерции относительно центра Моментом инерции тела (системы) относительно центра O называется скалярная величина, равная сумме произведений массы каждой точки тела (системы) на квадрат ее расстояния до этого центра z hiz mi y O x xi yi Моменты инерции точки относительно осей Ox, Oy, Oz равны 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 91
 2. 4. 8. Радиус инерции Если момент инерции системы относительно оси Ox равен Jx, а ее масса – М, то величина z hiz mi y O x xi yi называется радиусом инерции системы относительно оси Oх • Радиус инерции определяет расстояние от оси Oх до точки, в которой нужно сосредоточить всю массу тела (системы), чтобы момент инерции этой точки был равен моменту инерции всего тела (системы) 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 82
2. 4. 8. Радиус инерции Если момент инерции системы относительно оси Ox равен Jx, а ее масса – М, то величина z hiz mi y O x xi yi называется радиусом инерции системы относительно оси Oх • Радиус инерции определяет расстояние от оси Oх до точки, в которой нужно сосредоточить всю массу тела (системы), чтобы момент инерции этой точки был равен моменту инерции всего тела (системы) 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 82
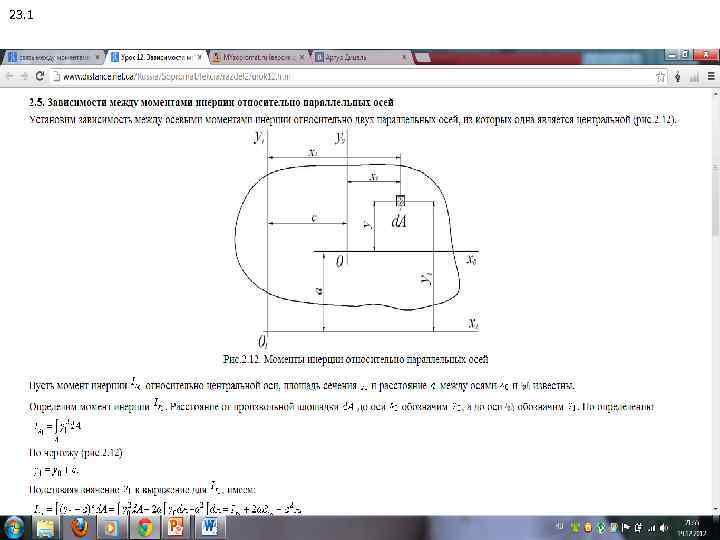 23. 1
23. 1
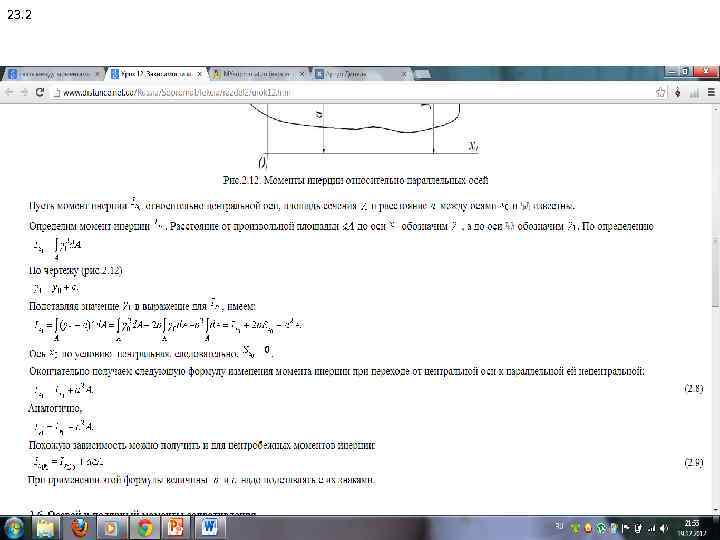 23. 2
23. 2
 24
24
 Запишем ІІ-ой закон Ньютона для точки: ma = F d ( mv ) = F dt Получим теорему об изменении количества движения точки в дифференциальной d( m ) форме: v mv = Q = F dt - количество движения точки
Запишем ІІ-ой закон Ньютона для точки: ma = F d ( mv ) = F dt Получим теорему об изменении количества движения точки в дифференциальной d( m ) форме: v mv = Q = F dt - количество движения точки
 d ( M r c ) Q = dt => dr c Q = M dt Q = M vc - количество движения системы - произведение массы системы и скорости ее центра масс
d ( M r c ) Q = dt => dr c Q = M dt Q = M vc - количество движения системы - произведение массы системы и скорости ее центра масс
 25
25
 Момент количества движения системы определяется как векторная сумма моментов количества движения точек, входящих в систему. n K 0 = n S K 0 = S r m v k=1 k k k
Момент количества движения системы определяется как векторная сумма моментов количества движения точек, входящих в систему. n K 0 = n S K 0 = S r m v k=1 k k k
 26
26
 Кинетическая энергия системы определяется как сумма кинетических энергий точек, входящих в систему. n 1 2 T = 2 S mkvk k=1
Кинетическая энергия системы определяется как сумма кинетических энергий точек, входящих в систему. n 1 2 T = 2 S mkvk k=1
 Кинетическая энергия системы. (Теорема Кёнига)
Кинетическая энергия системы. (Теорема Кёнига)
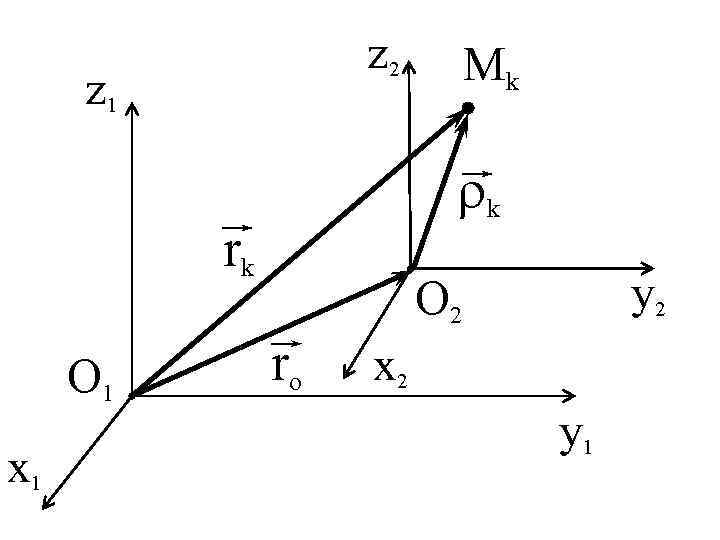 z 2 z 1 k rk O 1 x 1 Mk y 2 O 2 ro x 2 y 1
z 2 z 1 k rk O 1 x 1 Mk y 2 O 2 ro x 2 y 1
 01 x 1 y 1 z 1 - неподвижная система координат Система координат 02 x 2 y 2 z 2 перемещается поступательно. Вектор rk определяет положение точки относительно неподвижной системы координат, а вектор k - относительно подвижной системы координат.
01 x 1 y 1 z 1 - неподвижная система координат Система координат 02 x 2 y 2 z 2 перемещается поступательно. Вектор rk определяет положение точки относительно неподвижной системы координат, а вектор k - относительно подвижной системы координат.
 rk = r 0 + k Дифференцируем уравнение по времени. vk = v 0 + vk r - скорость точки относительно подвижной системы координат n 1 2 Tr = 2 S mkvk r k=1 - кинетическая энергия системы относительно подвижной системы координат
rk = r 0 + k Дифференцируем уравнение по времени. vk = v 0 + vk r - скорость точки относительно подвижной системы координат n 1 2 Tr = 2 S mkvk r k=1 - кинетическая энергия системы относительно подвижной системы координат
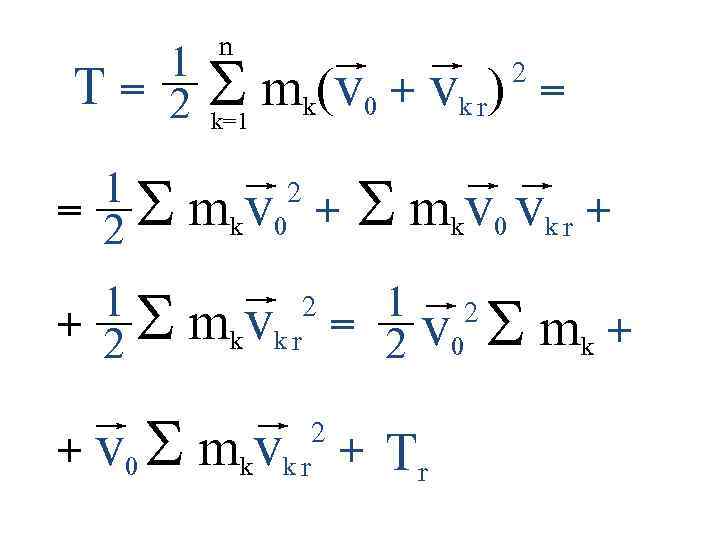 n 1 2 T = 2 S mk(v 0 + vk r) = k=1 1 = S 2 mkv 0 + S mkv 0 vk r + 1 + S 2 mkvk r 2 1 2 = v 0 S 2 2 + v 0 S mkvk r + Tr 2 mk +
n 1 2 T = 2 S mk(v 0 + vk r) = k=1 1 = S 2 mkv 0 + S mkv 0 vk r + 1 + S 2 mkvk r 2 1 2 = v 0 S 2 2 + v 0 S mkvk r + Tr 2 mk +
 c - радиус-вектор, определяющий положение центра масс системы относительно подвижной системы координат S mk k = c M Дифференцируем повремени: S mk vk r vc r = M
c - радиус-вектор, определяющий положение центра масс системы относительно подвижной системы координат S mk k = c M Дифференцируем повремени: S mk vk r vc r = M
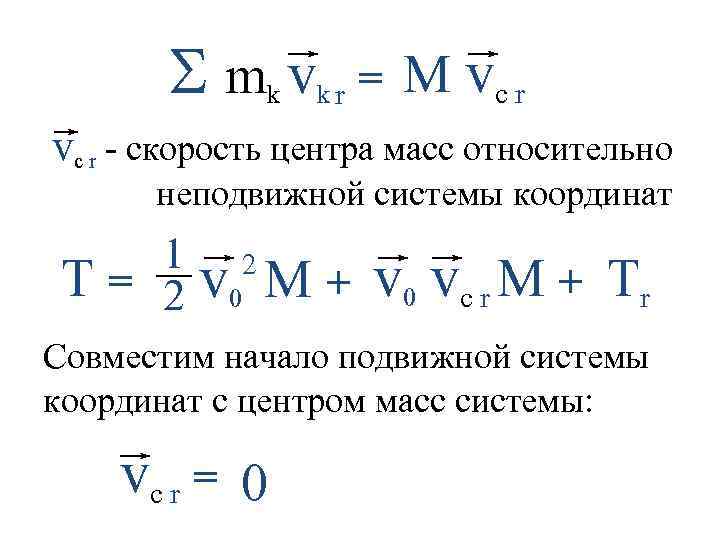 S mk vk r = M vc r - скорость центра масс относительно неподвижной системы координат 1 2 T = v 0 M + 2 v 0 vc r M + Tr Совместим начало подвижной системы координат с центром масс системы: vc r = 0
S mk vk r = M vc r - скорость центра масс относительно неподвижной системы координат 1 2 T = v 0 M + 2 v 0 vc r M + Tr Совместим начало подвижной системы координат с центром масс системы: vc r = 0
 1 2 T = 2 M v 0 + Tr Кинетическая энергия системы равна сумме кинетической энергии поступательного движения центра масс системы и кинетической энергии движения системы относительно центра масс.
1 2 T = 2 M v 0 + Tr Кинетическая энергия системы равна сумме кинетической энергии поступательного движения центра масс системы и кинетической энергии движения системы относительно центра масс.
 27
27
 Работа силы
Работа силы
 Прямолинейное перемещение тела.
Прямолинейное перемещение тела.
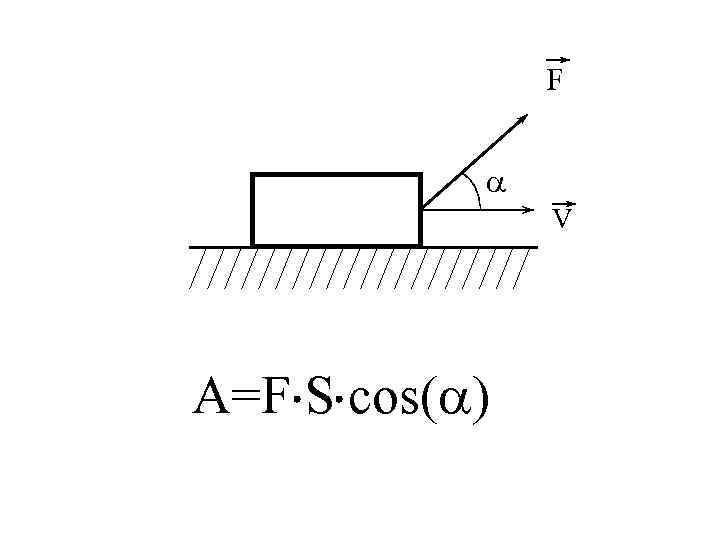 F V A=F S cos( )
F V A=F S cos( )
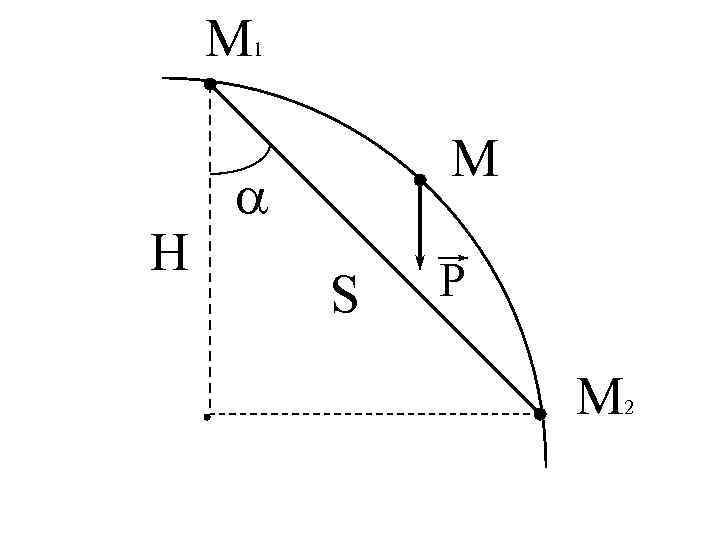
 Работа силы тяжести.
Работа силы тяжести.
 M H 1 M S P M 2
M H 1 M S P M 2
 Изменение положения тела по высоте определяется: H = S cos( ) Тогда работа на участке равна: A = P H = P S cos( ) 1, 2 Если тело опускают - работа положительная, если поднимают - отрицательная.
Изменение положения тела по высоте определяется: H = S cos( ) Тогда работа на участке равна: A = P H = P S cos( ) 1, 2 Если тело опускают - работа положительная, если поднимают - отрицательная.
 28 консервати вные си лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
28 консервати вные си лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
 29
29
 Внешние силы F e - силы, действующие на тела данной системы со стороны тел, не входящих в данную систему Внутренние силы F i - силы взаимодействия между телами данной системы.
Внешние силы F e - силы, действующие на тела данной системы со стороны тел, не входящих в данную систему Внутренние силы F i - силы взаимодействия между телами данной системы.
 30
30
 ТЕОРЕМА ИМПУЛЬСОВ ДЛЯ СИСТЕМЫ, ВЫРАЖЕННАЯ ЧЕРЕЗ ДВИЖЕНИЕ ЦЕНТРА МАСС. Изменение скорости центра масс системы за конечный промежуток времени равно импульсу внешних сил системы за тот же промежуток времени, деленному на массу всей системы. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 1. Для точки: изменение кинетической энергии точки на конечном ее перемещении равно работе приложенных к ней активных сил (касательные составляющие реакций неидеальных связей включаются в число активных сил): Для случая относительного движения: изменение кинетической энергии точки при относительном движении равно работе приложенных к ней активных сил и переносной силы инерции (см. "Частные случаи интегрирования"): 2. Для системы: изменение кинетической энергии системы на некотором перемещении ее точек равно работе приложенных к ней внешних активных сил и внутренних сил, приложенных к точкам системы, расстояние между которыми меняется: Если система неизменяема (твердое тело), то ΣAi=0 и изменение кинетической энергии равно работе только внешних активных сил. ТЕОРЕМА ИМПУЛЬСОВ (теорема количества движения в конечной форме). 1. Для точки: изменение количества движения точки за конечный промежуток времени равно сумме импульсов, приложенных к точке сил (или импульсу равнодействующей приложенных к точке сил) или в координатной форме: 2. Для системы: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил: или в координатной форме: Следствия: при отсутствии внешних сил количество движения системы есть величина постоянная; если внешние силы системы перпендикулярны некоторой оси, то проекция количества движения на эту ось есть величина постоянная.
ТЕОРЕМА ИМПУЛЬСОВ ДЛЯ СИСТЕМЫ, ВЫРАЖЕННАЯ ЧЕРЕЗ ДВИЖЕНИЕ ЦЕНТРА МАСС. Изменение скорости центра масс системы за конечный промежуток времени равно импульсу внешних сил системы за тот же промежуток времени, деленному на массу всей системы. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 1. Для точки: изменение кинетической энергии точки на конечном ее перемещении равно работе приложенных к ней активных сил (касательные составляющие реакций неидеальных связей включаются в число активных сил): Для случая относительного движения: изменение кинетической энергии точки при относительном движении равно работе приложенных к ней активных сил и переносной силы инерции (см. "Частные случаи интегрирования"): 2. Для системы: изменение кинетической энергии системы на некотором перемещении ее точек равно работе приложенных к ней внешних активных сил и внутренних сил, приложенных к точкам системы, расстояние между которыми меняется: Если система неизменяема (твердое тело), то ΣAi=0 и изменение кинетической энергии равно работе только внешних активных сил. ТЕОРЕМА ИМПУЛЬСОВ (теорема количества движения в конечной форме). 1. Для точки: изменение количества движения точки за конечный промежуток времени равно сумме импульсов, приложенных к точке сил (или импульсу равнодействующей приложенных к точке сил) или в координатной форме: 2. Для системы: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил: или в координатной форме: Следствия: при отсутствии внешних сил количество движения системы есть величина постоянная; если внешние силы системы перпендикулярны некоторой оси, то проекция количества движения на эту ось есть величина постоянная.
 31
31
 n Mac = k = 1 Fk S e e и - Теорема о движении центра масс системы F + F = 0 e и F = – F и F = – Mac Главный вектор сил инерции определяется как произведение массы системы на ускорение ее центра масс, взятое со знаком «–» . и и m F ac
n Mac = k = 1 Fk S e e и - Теорема о движении центра масс системы F + F = 0 e и F = – F и F = – Mac Главный вектор сил инерции определяется как произведение массы системы на ускорение ее центра масс, взятое со знаком «–» . и и m F ac
 32 1. Если система внешних сил такова, что их главный вектор равен нулю, т. е. , то центр масс либо находится в состоянии покоя (vc=0), либо движется равномерно и прямолинейно. 2. Если система внешних сил такова, что их главный вектор не равен нулю, т. е. , однако равна нулю сумма проекций всех сил на какую-либо из координатных осей , тогда проекция скорости центра масс на эту ось постоянна (vcz=const).
32 1. Если система внешних сил такова, что их главный вектор равен нулю, т. е. , то центр масс либо находится в состоянии покоя (vc=0), либо движется равномерно и прямолинейно. 2. Если система внешних сил такова, что их главный вектор не равен нулю, т. е. , однако равна нулю сумма проекций всех сил на какую-либо из координатных осей , тогда проекция скорости центра масс на эту ось постоянна (vcz=const).
 33
33
 Запишем ІІ-ой закон Ньютона для точки: ma = F d ( mv ) = F dt Получим теорему об изменении количества движения точки в дифференциальной d( m ) форме: v mv = Q = F dt - количество движения точки
Запишем ІІ-ой закон Ньютона для точки: ma = F d ( mv ) = F dt Получим теорему об изменении количества движения точки в дифференциальной d( m ) форме: v mv = Q = F dt - количество движения точки
 n Q = S mkvk k=1 v = r k k - количество движения системы - сумма количеств движений точек, входящих в систему Распишем выражение и поменяем суммирования и дифференцирования т. к. они не зависят друг от друга: n n dr k = d S m v Q = S mk k k k=1 dt dt k=1
n Q = S mkvk k=1 v = r k k - количество движения системы - сумма количеств движений точек, входящих в систему Распишем выражение и поменяем суммирования и дифференцирования т. к. они не зависят друг от друга: n n dr k = d S m v Q = S mk k k k=1 dt dt k=1
 d ( M r c ) Q = dt => dr c Q = M dt Q = M vc - количество движения системы - произведение массы системы и скорости ее центра масс
d ( M r c ) Q = dt => dr c Q = M dt Q = M vc - количество движения системы - произведение массы системы и скорости ее центра масс
 Запишем ІІ-ой закон Ньютона для системы точек: dvk = S F e + S F i S mk k k dt Меняя порядок суммирования и дифференцирования получим: d S m v = F e k k dt Теорема об изменении количества движения: d. Q = F e dt
Запишем ІІ-ой закон Ньютона для системы точек: dvk = S F e + S F i S mk k k dt Меняя порядок суммирования и дифференцирования получим: d S m v = F e k k dt Теорема об изменении количества движения: d. Q = F e dt
 34
34
 2. 5. 6. Закон сохранения импульса Важнейшим следствие данной теоремы является закон сохранения импульса Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется Например, 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 91
2. 5. 6. Закон сохранения импульса Важнейшим следствие данной теоремы является закон сохранения импульса Если главный вектор внешних сил, действующих на систему, равен нулю, то ее импульс сохраняется Если проекция главного вектора внешних сил, действующих на систему, на некоторую ось равна нулю, то проекция импульса системы на эту ось также сохраняется Например, 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 91
 35
35
 Пусть система состоит из n-материальных точек. Делим все силы, действующие на систему, на внешние и внутренние и для каждой точки запишем теорему об изменении кинетической энергии.
Пусть система состоит из n-материальных точек. Делим все силы, действующие на систему, на внешние и внутренние и для каждой точки запишем теорему об изменении кинетической энергии.
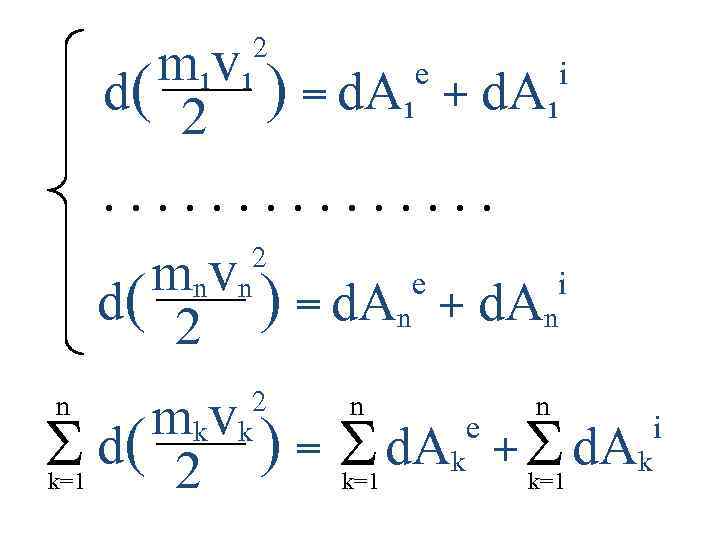 m 1 v 1 e i d( ) = d. A 1 + d. A 1 2. . . . 2 mnvn e i d( ) = d. An + d. An 2 2 mkv e i S d( ) = S d. Ak + d. Ak S 2 k=1 k=1 n 2 k n n
m 1 v 1 e i d( ) = d. A 1 + d. A 1 2. . . . 2 mnvn e i d( ) = d. An + d. An 2 2 mkv e i S d( ) = S d. Ak + d. Ak S 2 k=1 k=1 n 2 k n n
 mkv e i d ( ) = d. A + d. A S 2 k=1 n 2 k - сумма элементарных работ, произведенных всеми внешними и всеми внутренними силами e d. T = d. A + d. A i - теорема об изменении кинетической энергии системы в дифференциальной форме.
mkv e i d ( ) = d. A + d. A S 2 k=1 n 2 k - сумма элементарных работ, произведенных всеми внешними и всеми внутренними силами e d. T = d. A + d. A i - теорема об изменении кинетической энергии системы в дифференциальной форме.
 Если под действием внешних и внутренних сил системы она перемесилась из начального положения в конечное, то в интегральной форме теорема об изменении кинетической энергии будет иметь вид: T - T 0 = A + A e i
Если под действием внешних и внутренних сил системы она перемесилась из начального положения в конечное, то в интегральной форме теорема об изменении кинетической энергии будет иметь вид: T - T 0 = A + A e i
 Изменение кинетической энергии системы при перемещении ее из начального положения в конечное равна сумме работ внешних и внутренних сил.
Изменение кинетической энергии системы при перемещении ее из начального положения в конечное равна сумме работ внешних и внутренних сил.
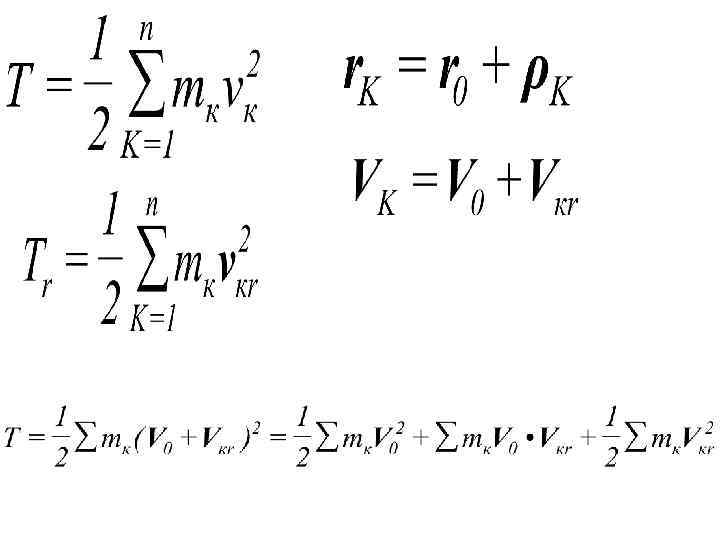
 36
36
 Теорема об изменении момента количества движения точки d (r m v ) = M e 0 dt d. K = e M 0 dt
Теорема об изменении момента количества движения точки d (r m v ) = M e 0 dt d. K = e M 0 dt
 Производная по времени от вектора момента количества движения точки равна моменту внешних сил относительно той же точки. Получим эту теорему для системы. Пусть система состоит из n-материальных точек. Разделим все силы, действующие на систему, на внешние и внутренние и для каждой точки запишем теорему об изменении количества движения точки.
Производная по времени от вектора момента количества движения точки равна моменту внешних сил относительно той же точки. Получим эту теорему для системы. Пусть система состоит из n-материальных точек. Разделим все силы, действующие на систему, на внешние и внутренние и для каждой точки запишем теорему об изменении количества движения точки.
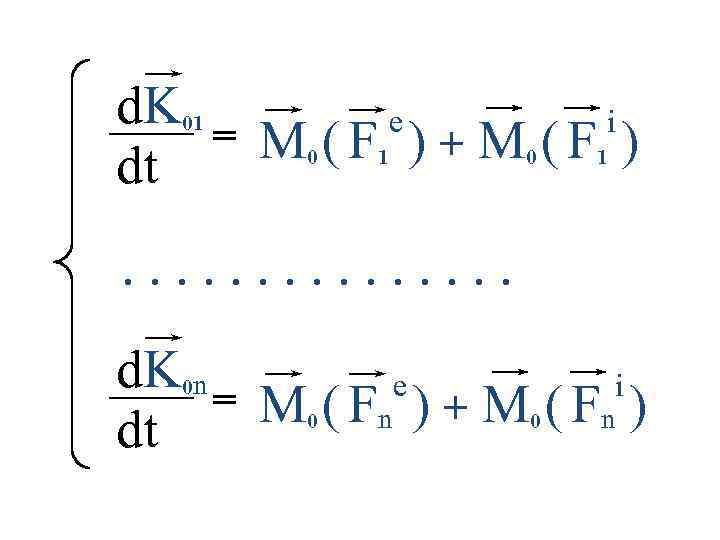 d. K = e i M ( F ) + M ( F ) dt 01 0 1 . . . . d. K n = e i M ( Fn ) + M ( Fn ) dt 0 0 0
d. K = e i M ( F ) + M ( F ) dt 01 0 1 . . . . d. K n = e i M ( Fn ) + M ( Fn ) dt 0 0 0
 Почленно сложим уравнения системы: n n n d. K k = e i S dt S M ( Fk ) + M ( Fk ) S k=1 k=1 0 0 d e S K k = M dt k=1 0 0 n 0 d. K = e M dt 0 0
Почленно сложим уравнения системы: n n n d. K k = e i S dt S M ( Fk ) + M ( Fk ) S k=1 k=1 0 0 d e S K k = M dt k=1 0 0 n 0 d. K = e M dt 0 0
 Следствия : 1) 2) Внутренними силами нельзя изменить момент количества движения системы. Если главный момент внешних сил системы равен нулю, то вектор момента внешних сил системы - величина постоянная. e Если M = 0 , то K = const 0 0
Следствия : 1) 2) Внутренними силами нельзя изменить момент количества движения системы. Если главный момент внешних сил системы равен нулю, то вектор момента внешних сил системы - величина постоянная. e Если M = 0 , то K = const 0 0
 3) d. K x = Mx e Если проекция главного момента внешних сил на какуюлибо ось равна нулю, то кинетический момент - величина постоянная. dt d. Ky = e My dt d. Kz = e Mz dt e Если Mx = 0 , то Kx = const
3) d. K x = Mx e Если проекция главного момента внешних сил на какуюлибо ось равна нулю, то кинетический момент - величина постоянная. dt d. Ky = e My dt d. Kz = e Mz dt e Если Mx = 0 , то Kx = const
 37 Из основного уравнения динамики вращательного движения следует, что Для замкнутой (изолированной) системы результирующий вектор момента всех внешних сил, действующих на тело, равен нулю и или Это утверждение представляет собой содержание закона сохранения момента количества движения: и формулируется следующим образом: если результирующий момент всех внешних сил относительно неподвижной осивращения тела равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Этот закон может быть обобщен на любую незамкнутую систему тел, если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.
37 Из основного уравнения динамики вращательного движения следует, что Для замкнутой (изолированной) системы результирующий вектор момента всех внешних сил, действующих на тело, равен нулю и или Это утверждение представляет собой содержание закона сохранения момента количества движения: и формулируется следующим образом: если результирующий момент всех внешних сил относительно неподвижной осивращения тела равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Этот закон может быть обобщен на любую незамкнутую систему тел, если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.
 38
38
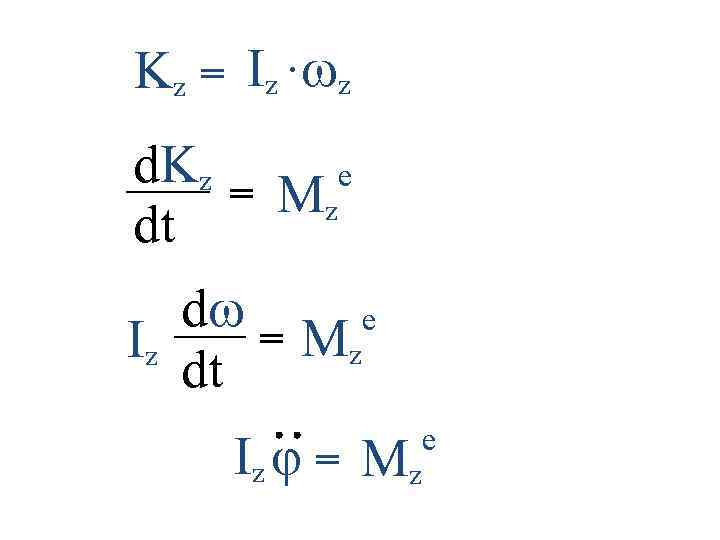 Kz = Iz ·wz d. Kz = e Mz dt dw e = Mz Iz dt Iz φ = Mz e
Kz = Iz ·wz d. Kz = e Mz dt dw e = Mz Iz dt Iz φ = Mz e
 39
39
 40
40
 2. 5. 26. Закон сохранения механической энергии • Необходимо подчеркнуть, что элементарные работы внешних и внутренних сил в общем случае не являются дифференциалами • Элементарные работы внешних и внутренних сил являются полными дифференциалами, если только эти силы потенциальные • В этом случае Теорема IV сумме кинетической и потенциальной энергии где E, равная системы, называется рассматриваемой системы являются Если все силы ее полной механической энергией • Дифференциал полной механической энергии равен нулю и мы потенциальными, то ее полная механическая энергия приходим к теореме остается постоянной при любом движении системы 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 110
2. 5. 26. Закон сохранения механической энергии • Необходимо подчеркнуть, что элементарные работы внешних и внутренних сил в общем случае не являются дифференциалами • Элементарные работы внешних и внутренних сил являются полными дифференциалами, если только эти силы потенциальные • В этом случае Теорема IV сумме кинетической и потенциальной энергии где E, равная системы, называется рассматриваемой системы являются Если все силы ее полной механической энергией • Дифференциал полной механической энергии равен нулю и мы потенциальными, то ее полная механическая энергия приходим к теореме остается постоянной при любом движении системы 2. 1. ОПРЕДЕЛЕНИЕ ССС 2. ДИНАМИКА СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 110


