Kinematics in Two Dimensions Position velocity acceleration

Kinematics in Two Dimensions • Position, velocity, acceleration vectors • Constant acceleration in 2 -D • Free fall in 2 -D Serway and Jewett : 4. 1 to 4. 3 Physics 1 D 03 - Lecture 4 1

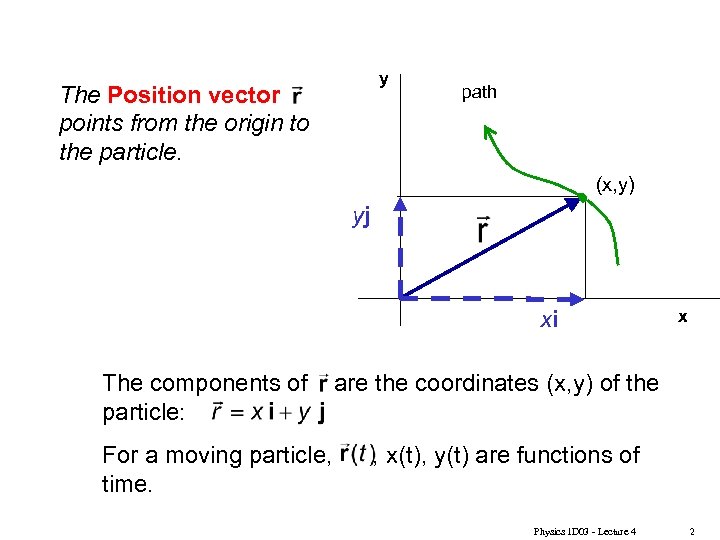y The Position vector points from the origin to the particle. path (x, y) yj xi The components of particle: For a moving particle, time. x are the coordinates (x, y) of the , x(t), y(t) are functions of Physics 1 D 03 - Lecture 4 2

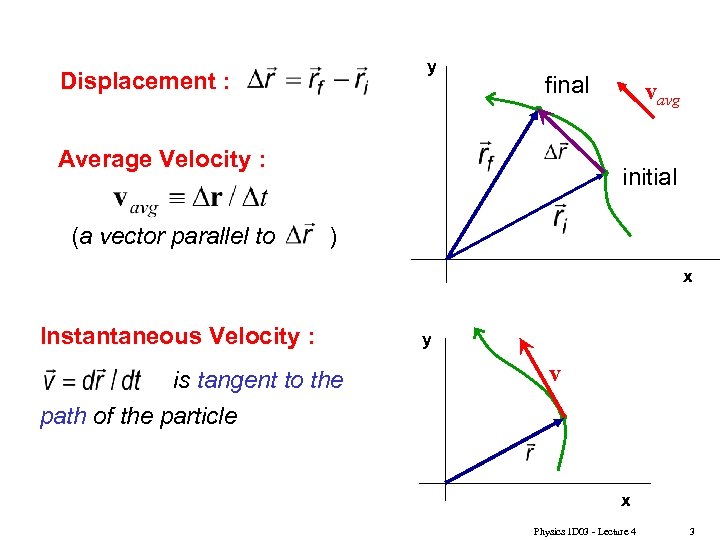y Displacement : final Average Velocity : (a vector parallel to vavg initial ) x Instantaneous Velocity : is tangent to the y v path of the particle x Physics 1 D 03 - Lecture 4 3

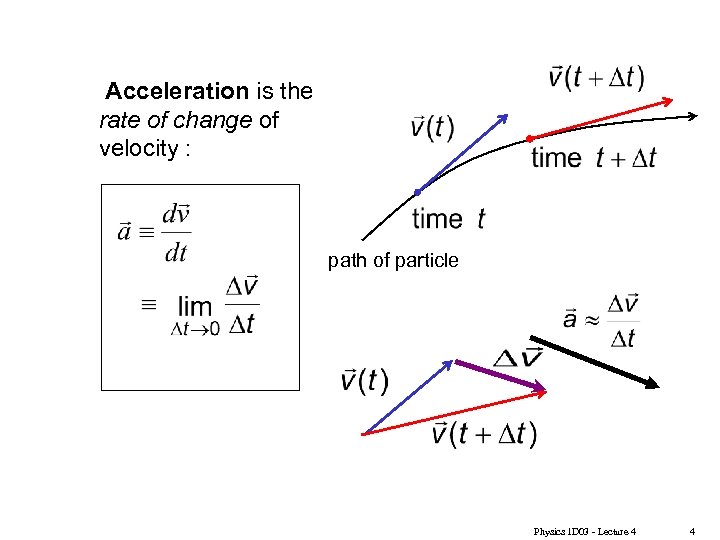Acceleration is the rate of change of velocity : path of particle Physics 1 D 03 - Lecture 4 4

a is the rate of change of v (Recall: a derivative gives the “rate of change” of function wrt a variable, like time). Velocity changes if i) speed changes ii) direction changes (even at constant speed) iii) both speed and direction change In general, acceleration is not parallel to the velocity. Physics 1 D 03 - Lecture 4 5

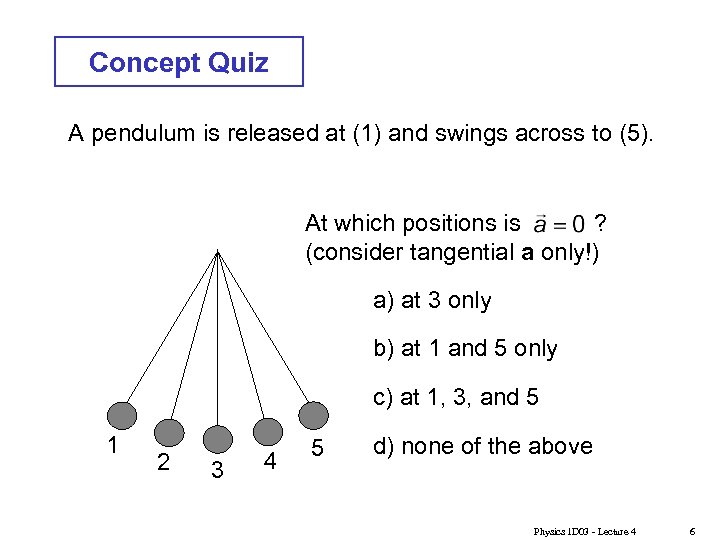Concept Quiz A pendulum is released at (1) and swings across to (5). At which positions is ? (consider tangential a only!) a) at 3 only b) at 1 and 5 only c) at 1, 3, and 5 1 2 3 4 5 d) none of the above Physics 1 D 03 - Lecture 4 6

Components: Each vector relation implies 3 separate relations for the 3 Cartesian components. (i, j, k, are unit vectors) We get velocity components by differentiation: the unit vectors are constants Physics 1 D 03 - Lecture 4 7

Each component of the velocity vector looks like the 1 -D “velocity” we saw earlier. Similarly for acceleration: Physics 1 D 03 - Lecture 4 8

Common Notation – for time derivatives only, a dot is often used: Physics 1 D 03 - Lecture 4 9

Constant Acceleration + Projectile Motion If is constant (magnitude and direction), then: Where are the initial values at t = 0. In 2 -D, each vector equation is equivalent to a pair of component equations: Example: Physics 1 D 03 - Lecture 4 10

Shooting the Gorilla Tarzan has a new AK-47. George the gorilla hangs from a tree branch, and bets that Tarzan can’t him. Tarzan aims at George, and as soon as he shoots his gun George lets go of the branch and begins to fall. Where should Tarzan be aiming his gun as he fires it? A) above the gorilla B) at the gorilla C) below the gorilla Physics 1 D 03 - Lecture 4 11

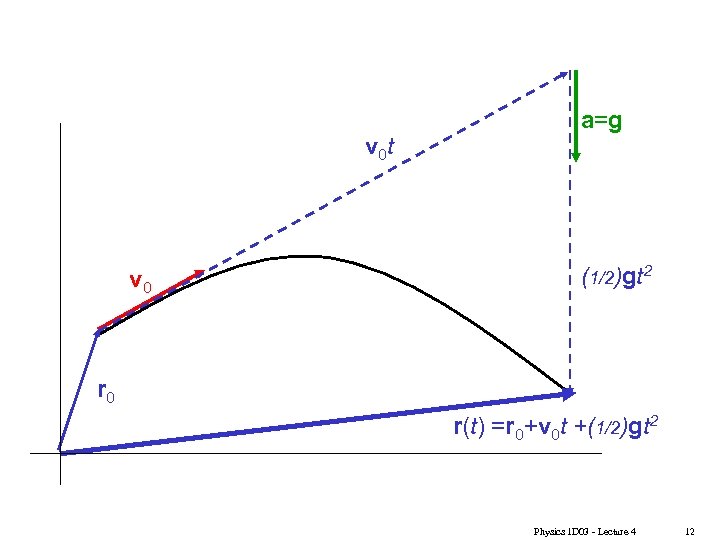v 0 t v 0 a=g (1/2)gt 2 r 0 r(t) =r 0+v 0 t +(1/2)gt 2 Physics 1 D 03 - Lecture 4 12

Concept quiz Your summer job at an historical site includes firing a cannon to amuse tourists. Unfortunately, the cannon isn’t properly attached, and as the cannonball shoots forward (horizontally) the cannon slides backwards off the wall. If the cannon hits the ground 2 seconds later, the cannonball will hit the ground: a) 2 seconds after firing 2 m/s 100 m/s b) 100 seconds after firing c) seconds after firing d) Other (explain) Physics 1 D 03 - Lecture 4 13

Example Problem A stone is thrown upwards from the top of a 45. 0 m high building with a 30º angle above the horizontal. If the initial velocity of the stone is 20. 0 m/s, how long is the stone in the air, and how far from the base of the building does it land ? Physics 1 D 03 - Lecture 4 14

Example Problem: Cannon on a slope. 100 m/s 30° 20° d How long is the cannonball in the air, and how far from the cannon does it hit? Try to do it two different ways: once using horizontal and vertical axes, once using axes tilted at 20 o. Physics 1 D 03 - Lecture 4 15

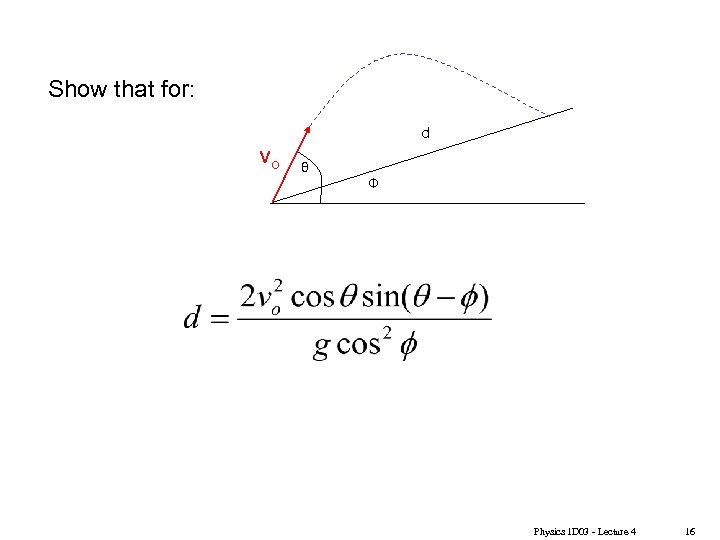Show that for: vo d θ Φ Physics 1 D 03 - Lecture 4 16

Summary • position vector points from origin to a particle • velocity vector • acceleration vector • for constant acceleration, we can apply 1 -D formulae to each component separately • for free fall in uniform , horizontal and vertical motions are independent Physics 1 D 03 - Lecture 4 17