Київський національний університет i м. Т. Шевченка

Київський національний університет i м. Т. Шевченка Інститут високих технологій Математика для біологів та хіміків Кратні та криволінійні інтеграли

2 Задамо у замкненій області D неперервну функцію двох змінних . D розби- вається на суб-області , площа яких відповідно . Це є Т -розбиття. довільна точка ( , )z f x y 0 1 1 , , . . . , n. D D D 0 1 1 , , . . . , n. S S S , k k k D Сума називається інтегральною сумою функції в області D з Т -розбиттям залежною від точок 1 0 ( , )n k k f S ( , )z f x y ( , ) k k ˗ найбільший розмір серед суб- комірок D k

3 Подвійним інтегралом функції по області D називається границя( , )z f x y 1 0 0 lim ( , ) n k k k n k. I f S що не залежить від Т -розбиття та вибору точок і позначається як ( , ) k k (. ) DI f x y d. S В Декартовій системі координат (. ) DI f x y dxdy

4 Властивості подвійного інтеграла ( , ) , constant D D Cf x y dxdy C 1 1 ( , )n n i i D D f x y dxdy Область D розбита на дві області D 1 та D 2 1 2( , ) D D D f x y dxdy

5 Якщо для функцій та в області D виконується нерівність , то 1 ( , )f x y 2 ( , )f x y 1 2 ( , ) D D f x y dxdy ( , ) j j D f x y dxdy f x y S Функція є неперервною у замкнутій області D площею S. В цій області існує точка , така що ( , )f x y( , ) j jx y

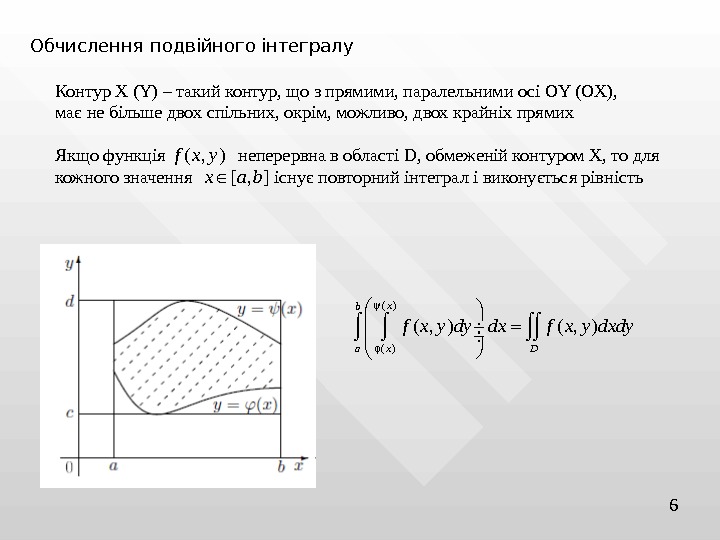
6 Обчислення подвійного інтегралу Контур Х (Y) – такий контур, що з прямими, паралельними осі OY (OX) , має не більше двох спільних, окрім, можливо, двох крайніх прямих Якщо функція неперервна в області D, обмеженій контуром Х, то для кожного значення існує повторний інтеграл і виконується рівність ( , )f x y [ , ]x a b ( ) ( , )x b a x D f x y dy dx f x y dxdy

7 Якщо функція неперервна в області D , обмеженій контуром Y , то для кожного значення існує повторний інтеграл і виконується рівність ( , )f x y [ , ]y c d ( ) ( , )y d c y D f x y dx dy f x y dxdy

8 Заміна змінних у подвійному інтегралі ( , ) DI f x y dxdy ( , )f x y D неперервна функція ( , ) , ( , )x u v y u v кожній точці відповідає єдина точка ( , ) x y D ( , ) u v G ( , ), ( , ) D G f x y dxdy f u v J dudv Якобіан переходу: ( , )u u v v u v J u v

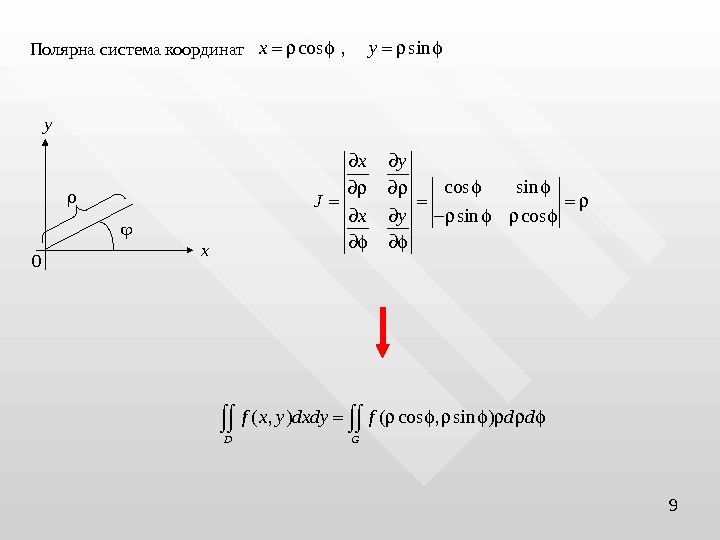
9 Полярна система координат cos , sinx y xy 0 cos sin cosx y J x y ( , ) ( cos , sin ) D G f x y dxdy f d d

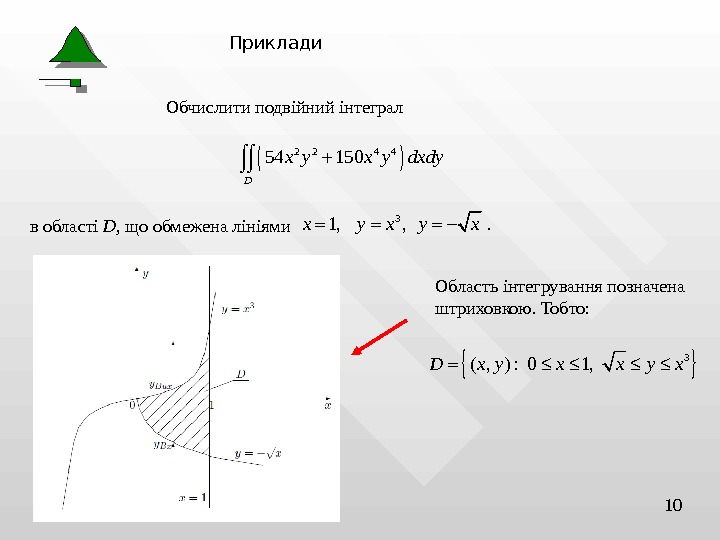
10 Приклади Обчислити подвійний інтеграл 2 2 4 4 54 150 D x y dxdy в області D , що обмежена лініями 3 1, , . x y x Область інтегрування позначена штриховкою. Тобто: 3 ( , ) : 0 1, D x y x

11 Переходимо від подвійного інтегралу до повторного на області D : 3 1 2 2 4 4 054 150 x D x. I x y dxdy dx x y dy 3 3 32 2 4 4 2 3 4 5 2 9 3/ 2 4 15 5/ 2 11 7 / 2 19 13/ 254 150 18 30 18 18 30 30 x x xx y dy x y x x x x x обчислюємо внутрішній інтеграл

121 11 7 / 2 19 13/ 2 0 1 1 12 9 / 2 20 15/ 2 0 018 18 30 30 18 18 2 30 30 2 12 9 20 15 3 3 4 4 11. 2 2 I x x dx x x Виконуємо зовнішнє інтегрування і маємо

13 Потрійний інтеграл В замкнутій області V задано неперервну функцію . Розіб’ємо область V на скінчене число менших за об’ємом областей . Їх об’єми відповідно . У кожній області V k виберемо довільну точку і утворимо суму ( , , )f x y z V 0 1 1 , , . . . , n. V V V ( , , ) k k V 1 0 ( , , )n k k k f V Потрійним інтегралом функції по області V є границя( , , )f x y z 1 0 0 lim ( , , ) n k k n k. I f V ( , , ) VI f x y z dxdydz

14 Властивості потрійного інтеграла ( , , ) , V V Cf x y z dxdydz C const 1 1 ( , , ) n n i i V V f x y z dxdydz Якщо область V розбита поверхнями скінченої площі на дві області V 1 та V 2 , що не перетинаються, то 1 2( , , ) + ( , , ) V V V f x y z dxdydz

15 Якщо і , тоді ( , , ) , ( , , ) f x y z V ( , , ) f x y z ( , , ) V V f x y z dxdydz Якщо функція є неперервною у замкненій області V , то в цій області існує точка , така що ( , , )f x y z ( , , ) s s sx y z ( , , ) s s s V f x y z dxdydz f x y z V

16 Обчислення потрійного інтегралу Якщо функція задана і неперервна в області . Нехай область V обмежена знизу поверхнею , зверху – поверхнею , а з боків — циліндрічною поверхнею, твірні якої паралельні осі OZ. Нехай D – проекція області V на площину XOY. Припустимо додатково, що для будь- якої точки області D , що обмежена кривими та для . Тоді потрійний інтеграл: ( , , )f x y z 3 V R 1 ( , )z f x y 2 ( , )z f x y 1 2 ( , )f x y ( , ) x y 1 ( )y y x 2 ( )y y x , x a b 2 2 1 1 ( ) ( , )( , , ) y x f x y b V a y x f x y z dxdydz dx dy f x y z dz

17 Дано загальні формули переходу до криволінійних координат ( , , ), ( , , ). x u t w y u t w z u t w Функції неперервні і мають неперервні похідні в області . Між точками областей і V ц і формули встановлюють взаємно однозначну відпо- відність. Тоді ( , , ), ( , , ) u t w ( , , ), ( , , ) V f x y z dxdydz f u t w J dudtdw Тут J – якобіан переходу від простору V до простору u u u J t t t w w w

18 Циліндрична система координат cos , sin , x y z z cos sin 0 sin cos 0 0 0 1 x y z J x y z z ( , , ) cos , sin , V f x y z dxdydz f z d d dz

19 сферична система координат cos sin , cosx r y r z r 2 sin cos sin sin cos 0 cos cos sin sinx y z r r r x y z J r r r x y z r 2( , , ) cos sin , cos sin V f x y z dxdydz f r r d d dr

20 Приклади Обчислити об’єм тіла, обмеженого поверхнями 2 2 36 , / 3, 0 z x y z Зобразимо область Т, що зайнята тілом, помітивши, що обмежуючі поверхні 2 2 1 : 6 , z 0 V x y z Півсфера з центром в точці 0 і радіусом R = 6 2 2 : , 0 3 x y V z z Півконус з центром в точці

21 Перетином областей V 1 та V 2 знайдемо як розв’язок системи 2 2 2 2 6 , 3 , 0. x y z z 2 2 4 6 2 6, 3 z z z ці області перетинаються по колу в площині 2 2 2 3 3 x y 3 z З огляду на симетрію обмежуючих поверхонь, доцільно використовувати сферичну систему координат: cos sin , cosx r y r z r маємо 2 2 2 2 sin , x y r x y z r 1 2 2 2 : 6; : sin 3 cos tg 3 / 3 V r r

22 Визначаємо області зміни координат: 0 6; 0 2 ; 0 / 3. r Обчислюємо об’єм тіла 6 6 2 / 3 2 3 0 0 0 1 sin ( cos ) 3 72 2 1 1 / 2 72 . V r dr d d r

23 Фізичний смисл потрійного інтегралу Нехай — розподіл об’ємної густини деякого тіла, об’ємом V. Тоді його маса буде визначатись інтегралом ( , , ) x y z ( , , ) Vm x y z dxdydz Збудження атомів у молекулярному кристалі призводить до появи дипольного моменту. Це збудження, рухаючись всередині об’єкту призводить до виникнення локальних струмів, що індукують поле в довільній точці. Це локальне електричне поле може бути знайденим з обчислення потрійного інтегралу по об’єму об’єкту (частинки)

24 незбуджений атом Збудженгий атом ( , ) kj t r 2 0( ) ( , ) ( ) i ik k VE k G j d r r r Електродинамічна функція Гріна (фотонний пропагатор) середовища, куди поміщено частинку об’ємом V

25 Додатково про властивості потрійного інтегралу Нехай функція визначена в області об’ємом V така, що( , , )f x y z ( ; ; ) inf ( , , ) x y zm f x y z нижня межа значень функції на множині її області визначення верхня межа значень функції на множині її області визначення ( ; ; ) sup ( , , ) x y z. M f x y z ( , , )m V f x y z dxdydz M V

26 Криволінійні інтеграли A B просторово гладка або кусково гладка крива 3 L R В кожній точці визначена неперервна функція . Крива розбита на n частин точками A i . Нехай l i довжина дуги A i -1 A i . — точка на кожній і -й дузі( , , )M x y z L ( , , ) ( )f x y z f M A 0 A 1 A n -1 A i- 1 A i ( , , ) i i. M 1 ( )n n i i i. I f M l Інтегральна сума для функції по дузі AB . Нехай max , 1, il i n ( , , )f x y z

270 1 1 lim ( ) n n i i. I f M l Якщо існує границя інтегральної суми, що не залежить від способу розбиття дуги АВ та від вибору на ній точок, то ця границя є к риволінійним інтегралом першого роду від функції по дузі АВ : ( , , )f x y z ( , , ) L ABI f x y z dl Оск і льки у формулах, що визначають криволінійні інтеграли довжина дуги , то 0 il 3 : ( , , ) 2 : ( , ) AB BAD f x y z dl D f x y dl

28 Властивості криволінійних інтегралів 1 -го роду 1. , l – довжина дуги АВ 1 AB AB dl dl l 2. Криволінійний інтеграл 1 -го роду не залежить від напрямку шляху інтегрування ( , ) AB BA f x y dl 3. Якщо для з функцій та існує криволінійний інтеграл 1 -го роду вздовж кривої АВ, то для ( , )f x y ( , )F x y af x y b x y ( , ) AB AB AB F x y dl a f x y dl b x y dl

294. Адитивність. Якщо дуга АВ складається з двох дуг АС та СВ А С В ( , ) AB AC CB f x y dl 5. Збереження знаку. Якщо на кривій АВ , то( , ) 0 f x y ( , ) 0 AB f x y dl 6. Оцінка модуля інтеграла. Якщо функція — інтегрована на кривій АВ , то функція також є інтегрованою на АВ , і справедлива нерівність ( , )f x y ( , ) AB AB f x y dl

31 Обчислення криволінійного інтеграла першого роду Інтеграл по тривимірній кривій а) якщо крива задана параметрично 3 AB R 1 2( ), ( ), . x x t y y t z z t t то 2 1 2 2 2 ( , , ) ( ), ( ) ( ) t AB t f x y z dl f x t y t z t dt

32 Інтеграл по плоскій кривій а) якщо крива задана параметрично 2 AB R 1 2( ), ( ), . x x t y y t t то 2 1 2 2 ( , ) ( ), ( ) ( ) t AB t f x y dl f x t y t dt б) якщо крива задана рівнянням або то 2 AB R ( ), , y y x a x b ( ), , x x y c y d 2 ( , ) , ( ) 1 ( ) b AB a f x y dl f x y x dx 2 ( , ) ( ), 1 ( ) d AB c f x y dl f x y y x y dy xy dx dydl 2 2 2 dl dx dy x dt y dt

33 в) Крива задана у полярній системі координат: то 2 AB R ( ) , , 2 2 ( , ) ( ) cos , ( ) sin ( ) AB f x y dl f d

A i -1 34 Криволінійні інтеграли другого роду Задано гладку або кусково гладку криву , яка обмежена точками А і В. В кожній точці задана вектор-функція , де функції — неперервні на кривій L. ( , , )F x y z P x y z i Q x y z j R x y z k r r 3 L R ( , , ), ( , , )P x y z Q x y z R x y z A B A 1 A n -1 A i Кожній дузі поставимо у відповідність вектор довжиною . Нехай 1 i i. A A 1 , , i i i. A A S x y z uuuuur i i. S l uuur max , 1, il i n i S uuur( , , ) i i. M 1 1 ( ) ( )n n n i i i i i. I F M S P M x Q M y R M z uuur r Інтегральна сума вектор-функції вздовж кривої L від точки А до точки В( , , )F x y z r

35 Якщо існує границя інтегральної суми Яка не залежить від способу розбиття дуги АВ та від вибору точок М і , то така границя називається криволінійним інтегралом другого роду від вектор-функції по дузі АВ. 0 1 lim ( ) n i i i F M S uuur r ( , , )F x y z r 1( , , ) lim ( ) ( )AB AB n i i i n i. F x y z dl P x y z dx Q x y z dy R x y z dz P M x Q M y R M z r r

36 Для криволінійного інтегралу другого роду має місце рівність AB BA Pdx Qdy Rdz криволінійний інтеграл другого роду на площині 1( , ) lim ( ) AB AB n i i n i. F x y dl P x y dx Q x y dy P M x Q M y r r

37 Обчислення криволінійних інтегралів другого роду а) крива задана параметрично 3 AB R ( ), x x t y y t z z t А : t = t AB : t = t B початкова точка кінцева точка кривої ( , , ) ( ( ), ( )) ( ) ( ( ), ( )) ( )B AAB t t. P x y z dx Q x y z dy R x y z dz P x t y t z t x t Q x t y t z t y t R x t y t z t dt

38 б) крива задана на площині параметрично 2 AB R ( ), x x t y y t ( , ) ( ( ), ( )) ( ) B At AB t P x y dx Q x y dy P x t y t x t Q x t y t dt в) крива задана на площині рівнянням , початковій точці кривій відповідає , а кінцевій точці . Тоді 2 AB R ( )y y x Ax x Bx x ( , ) ( , ( )) ( ) B Ax AB x P x y dx Q x y dy P x y x Q x y x dx крива задана на площині рівнянням , початковій точці кривій відповідає , а кінцевій точці . Тоді 2 AB R ( )x x y Ay y By y ( , ) ( ( ), ) B Ay AB y P x y dx Q x y dy P x y y x y Q x y y dy

39 Приклади Обчислити інтеграл від точки А(0; 0) до точки В(1; 1) вздовж: (а) – прямої (б) – параболи ( , ) ABI x y dl r r y x 2 y x І. ІІ. ( , ) x yx y ye xe r r r 2 ( , ) 2 x yx y y e yxe r r r

40 Розв’язок І (а): для прямої , звідси маємо , y x dy dx 1 0 0 AB xdy ydx x x dx І(б): для параболи , звідси 2 , 2 y x dy xdx 1 1 2 2 2 0 0 1 2 3 AB xdy ydx x x dx

41ІІ (а): для прямої , звідси маємо , y x dy dx 1 1 2 2 0 02 2 3 1 AB y dx yxdy x x dx ІІ(б): для параболи , звідси 2 , 2 y x dy xdx 1 1 2 4 3 4 0 02 2 2 5 1 AB y dx xydy x x x dx

42 Зв’язок між криволінійними інтегралами першого та другого роду Нехай α та β – кути, які утворює з осями координат дотична до кривої АВ у точці М ( х ; у ). Напрям дотичної відповідає напряму руху точки М від початку кривої (А) до її кінця (В). Згадуємо геометричний смисл ди- ференціала функції та диференціала дуги кривої: cos , cosdx dl dy dl ( , ) cos AB AB P x y dx Q x y dy P x y Q x y dl криволінійний інтеграл другого роду криволінійний інтеграл першого роду

43 Фізичний смисл криволінійного інтегралу Робота сили, що діє на матеріальну точку, яка рухається вздовж визначеної траекторії А В Робота сили F при переміщенні матеріальної точки на величину dl d. A F dl r r ABA F dl r r Визначимо проекції векторів та : тоді ( )F r r r( )F r rr dl r ( ) ( , , ) x y z. F r P x y z e Q x y z e R x y z e r r r x y zdl dxe dye dze r r ( , , ) ABA P x y z dx Q x y z dy R x y z dz

44 Приклад. Робота сили притяжіння коли матеріальна точка маси m рухається у полі гравітаційного центру M F r M m 2 rm. M F e r r r 2 2 2( ) ( ) g AB AB m. M x m. M y m. M z A Fdl dx dy dz r r r 1 r 2 r 3 3 1 g AB AB AB xdx ydy zdz rdr A m. M d r r r 2 11 1 1 g ABA m. M d m. M r r r залежить тільки від початкової та кінцевої точок траекторії, а не від її вигляду А В

45 Криволінійні інтеграли другого роду по замкненій кривій однозв’язна область двозв’язна область тризв’язна область додатно-орієнтований контур від’ємно-орієнтований контур

46 Криволінійні інтеграли другого роду по замкненій криволінійний інтеграл по замкненому додатно орієнтованому контуру L : ( , ) LI P x y dx Q x y dy Ñ Область G R 3 називається поверхнево — однозв ’ язною або однозв ’ язною, якщо на будь-який замкнений контур L G можна натягнути поверхню, що цілком лежить в області G . Відповідно криволінійний інтеграл по замкненому додатно орієнто- ваному контуру L R 3 ( , , ) LI P x y z dx Q x y z dy R x y z dz Ñ

47 Теорема: Якщо функції і та їх частині похідні першого порядку неперервні в замкнутій однозв’язній області D R 2 , що обмежена кусково-гладкою додатно орієнтованою кривою L , то має місце формула Гріна ( , )P x y ( , )Q x y ( , ) L D Q x y P x y dx Q x y dy dxdy x y Ñ D L

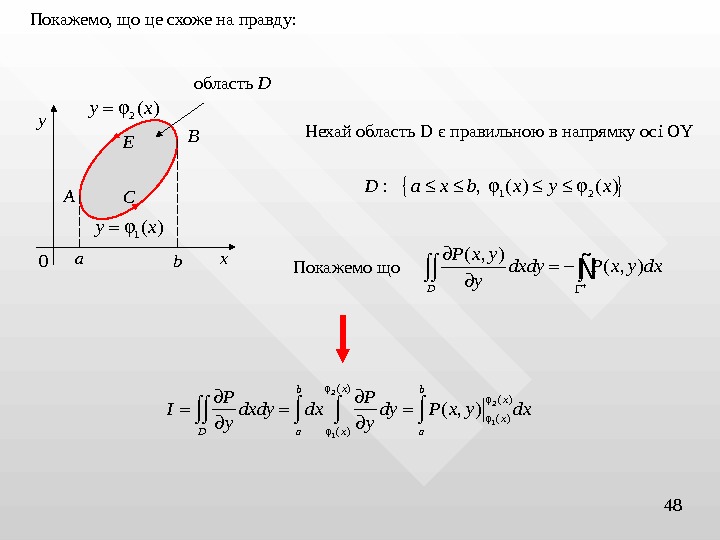
48 Покажемо, що це схоже на правду: область D Нехай область D є правильною в напрямку осі OY 1 2: , ( )D a x b x y x Покажемо що ( , ) D P x y dxdy P x y dx y Ñ 2 2 1 1 ( ) ( ) ( , )x b b x x D a x a P P I dxdy dx dy P x y dx y y xy A B C E 1 ( )y x 2 ( )y x a b

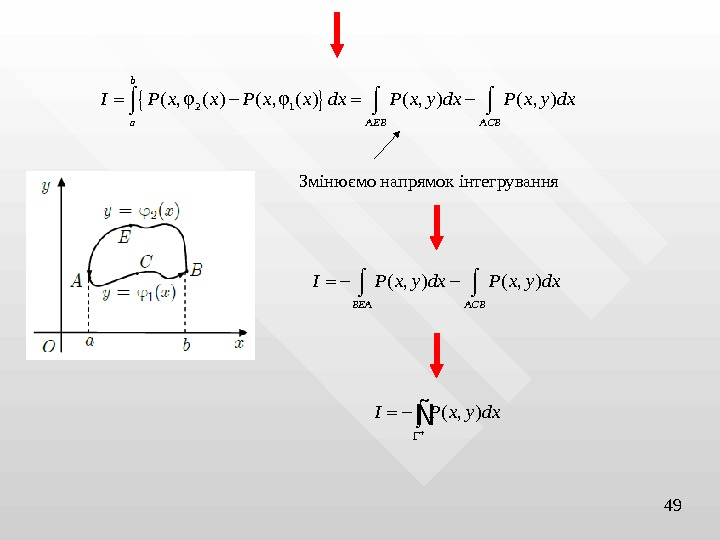
492 1( , ( ) ( , )b a AEB ACBI P x x dx P x y dx Змінюємо напрямок інтегрування ( , ) BEA ACBI P x y dx ( , )I P x y dx Ñ

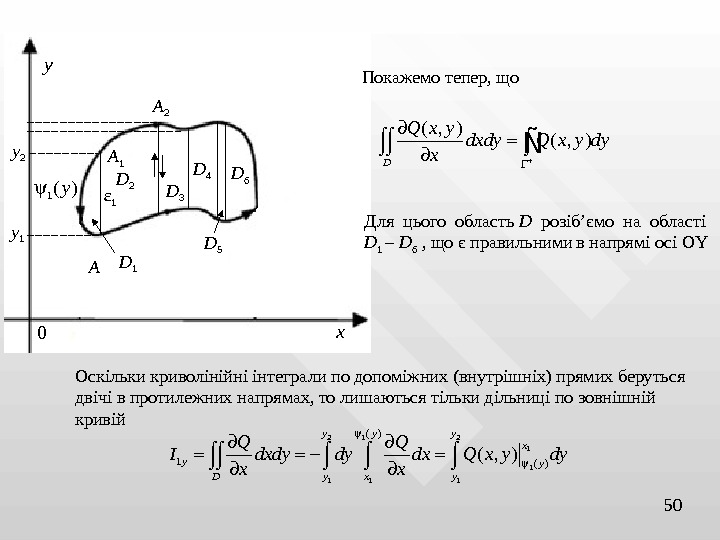
D 2 D 1 D 3 D 4 D 5 D 6 xy 0 y 1 y 2 50 Покажемо тепер, що ( , ) D Q x y dxdy Q x y dy x Ñ Для цього область D розіб’ємо на області D 1 – D 6 , що є правильними в напрямі осі OY Оскільки криволінійні інтеграли по допоміжних (внутрішніх) прямих беруться двічі в протилежних напрямах, то лишаються тільки дільниці по зовнішній кривій 1 ( ) y 2 1 1 1 ( )( , )y y y x y y D y x y Q Q I dxdy dy dx Q x y dy x x А А 1 ε 1 А

512 1 1 1 ( ( ), ) ( , )y y y A AI Q y y Q x y dy Змінюємо напрямок інтегрування 1 11 ( , ) y A AI Q x y dy І так далі: 1 1 1 6 1( , ) ( , ). . . ( , ) ii D D A A Q x y dxdy Q x y dy x x Q x y dy Ñ Ñ

52 М и бачили, що існують ситуації, коли величина криволінійного інтегралу другого роду не залежить від форми шляху інтегрування. Для таких випадків справедливою є така теорема: Теорема : Якщо функції і та їх частинні похідні є неперервними в замкненій однозв’язній області D , то мають місце такі рівносильні( , )P x y ( , )Q x y ( , )P x y y ( , )Q x y x твердження: 1. Інтеграл не залежить від форми шляху, що з’єднує точки А і В , 2. , де L – будь-який контур, що лежить в області D ( , ) 0 L P x y dx Q x y dy Ñ ( , ) ABI P x y dx Q x y dy AB D 3. В усіх точках області D виконується рівність Q P x y

534. Підінтегральний вираз є повним диференціалом деякої функції , визначеної в області D. ( , )P x y dx Q x y dy ( , )u x y Доведемо цю теорему Ідея доведення : якщо теорема виконується, то з кожного пункту її твердження слідує інший пункт Треба вивести з одного твердження інше, наприклад, за схемою: 1. 2. 3. 4. 1.

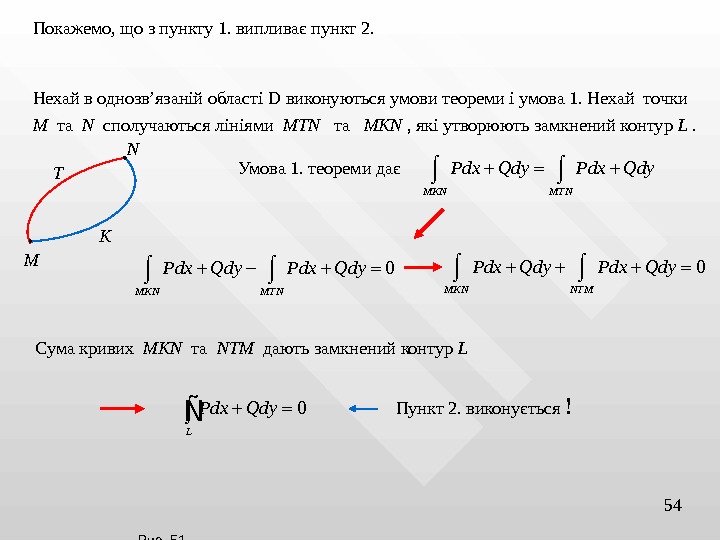
54 Рис. 51 Згідно з умовою N М T KПокажемо, що з пункту 1. випливає пункт 2. Нехай в однозв’язаній області D виконуються умови теореми і умова 1. Нехай точки M та N сполучаються лініями MTN та MKN , які утворюють замкнений контур L . Умова 1. теореми дає 0 MKN MTN Pdx Qdy 0 MKN NTM Pdx Qdy Сума кривих MKN та NTM дають замкнений контур L 0 L Pdx Qdy Ñ Пункт 2. виконується !

Покажемо як з пункту 2. випливає пункт 3. Застосуємо до рівняння теорему Гріна 550 L Pdx Qdy Ñ 0 L D Q P Pdx Qdy x y Ñ Оскільки контур L – довільний, то для виконання цього рівняння необхідно 0 Q P x y Пункт 3. виконується !

56 Доведемо тепер, що з твердження 3. випливає пункт 4. Для заданих у теоремі функцій і знайдемо функцію , яка задовольняє рівностям та з урахуванням твердження 3. ( , )P x y ( , )Q x y ( , )u x y u P x u Q y Q P x y 2 2 , Q u P u x x y y y x Оскільки , то Q P x y 2 2 u u x y y x це відповідає теоремі про рівність мішаних похідних для неперервно диференційовної в області D функції . Оскільки , то ( , )u x y u u du dx dy x y du Pdx Qdy виконується твердження 4. !

57 Доведемо тепер, що з пункту 4. випливає пункт 1. Якщо , а M і N початкова і кінцева точки довільної кривої l ( l D ) , то du Pdx Qdy ( )N M MN MN Pdx Qdy du u u N u M Останній вираз не залежить від форми кривої l , а тільки від точок M і N на ній, тобто умова 1. виконується. Зокрема, якщо крива замкнена, то цей інтеграл дорівнює н y лю.

58 Звідси випливає, що 0 0( , ) x yu x y Pdx Qdy де точки , D – область визначення функції та , і криволінійний інтеграл не залежить від шляху інтегрування, а тільки від початкової та кінцевої точок цього шляху 0 0 0 ( , ), ( , ) M x y D ( , )P x y ( , )Q x y 0 0 0( , ) y x x yu x y P x y dx Q x y dy C контур вибирається у вигляді ломаної з відріз- ків прямих паралельних осям координат

59 Приклади Користуючись формулою Гріна, обчислити інтеграл по контуру L , що є колом 5 8 ( 2 ) (3 ) L x y dx x y dy Ñ 2 2 2 x y r Розв’язання. Функції та і їх похідні є неперервними в замкненому колі 5 ( , ) 2 P x y 8 ( , ) 3 Q x y 2, 3 P Q y x 2 2 2 x y r виконуються умови теореми Гріна. Звідси 5 8 2 ( 2 ) (3 ) 3 ( 2) 5 5 5 L D D x y dx x y dy dxdy S r Ñ

60 Площа плоскої області D , що обмежена кривою L , обчислюється так: ( ) LS y x dx Ñ ( ) LS x y dy Ñ Поклавши а , отримаємо з формули Гріна 0 P Q x D L dxdy S xdy ÑD L Поклавши а , отримаємо з формули Гріна P y 0 Q D L dxdy S ydx Ñ 1 2 LS xdy ydx Ñ

61 Приклад: Обчислити площу фігури, обмеженої еліпсом: cos 0 2 sinx a y b xy ab Розв’язок: Приймаючи до уваги симетрію фігури, знайдемо площу її чверті / 2 1/ 4 0 / 2 / 2 2 2 0 0 0 1 1 cos sin 2 2 2 4 LS a xdy ydx a b b a d ab ab d d Ñ S ab

62 Приклад: Обчислити площу фігури, обмеженої петлею декартового листа : Запишемо дане рівняння у параметричному вигляді, покладаючи 2 3 33 3 , 1 1 at at x y t t Геометрично параметр – кутовий коефіцієнт полярного радіуса M . Точка М опише всю петлю кривої при зміні t від 0 до . /t y x 2 2 3 2 01 9 2 2 (1 ) L a t dt S xdy ydx t Ñ

632 2 2 3 2 3 3 2 0 0 2 2 39 3 (1 ) 3 lim (1 ) 2 3 1 3 lim 2 1 2 a t dt a d t a S t d t t t a a t

64 Поверхневі інтеграли першого роду Визначення. Поверхня називається гладкою, якщо в кожній точці існує дотична площина і при переході від точки до точки положення цієї дотичної площини змі- нюється неперервно. Поверхня, яка складається із скінченного числа неперервно сполучених гладких поверхонь, називається кусково-гладкою.

65 суб-поверхня і , на якій вибрано точку – кусково-гладка поверхня на якій визначена неперервна функція . Поверхня розбита на n частинних суб- поверхонь і без спільних внутрішніх точок. Площа кожної такої суб-поверхні ( , , )f x y z i ( , , ) i i. M 1 ( )n n i i i. I f M Інтегральна сума для функції по поверхні ( , , )f x y z

66 Якщо існує границя ( – найбільший розмір суб- поверхні), яка не залежить від способу розбиття поверхні та вибору точок М і , то ця границя називається поверхневим інтегралом першого роду від функції по поверхні 0 1 lim ( ) n i i i f M ( , , )f x y z 0 1 1( , , ) lim ( ) n n i if x y z d f M

67 Властивості поверхневого інтегралу І-го роду 1. Якщо S – площа поверхні , то d S 2. Якщо для з функцій існує поверхневий інтеграл І-го роду, то для функції також існує поверхневий інтеграл І-го роду ( , , )f x y z ( , , )g x y z ( , , ), ( , const)f x y z g x y z ( , , )f x y z g x y z d f x y z d g x y z d 3. Якщо поверхня складається з частин 1 та 2 ( ), а перетин поверхонь 1 та 2 складається лише з межі, що їх відокремлює, то 1 2( , , )f x y z d

684. Якщо на поверхні функція , то 5. Для інтегрованої по поверхні функції справедлива нерівність ( , , )f x y z 6. Якщо функція неперервна на поверхні , то на цій поверхні існує точка така, що де S – площа поверхні ( , , ) 0 f x y z d ( , , ) |f x y z d ( , , )f x y z ( , , ) x y z ( , , )f x y z d S f x y z

69 Поверхня задана рівнянням і будь-яка пряма, паралельна вісі OZ , перетинає поверхню лише в одній точці однозначно проектується на площину XOY. неперервна із своїми похідни — ми першого порядку в області D xy ( , )z z x y ( , )z x y D xy 2 2 ( , , ) ( , , ( , )) 1 ( , ) xy x y Df x y z d f x y z x y dxdy Якщо

70 Якщо поверхня задана рівнянням і її проекція на вісь XOZ є D xz( , )y y x z 2 2 ( , , ) ( , ), ) 1 ( , ) xz x z Df x y z d f x y x z z y x z dxdz Якщо поверхня задана рівнянням і її проекція на вісь YOZ є D yz( , )x x y z 2 2 ( , , ) ( ( , ), , ) 1 ( , ) yz y z Df x y z d f x y z dydz

71 Приклад : Обчислити поверхневий інтеграл першого роду 4 2 3 I z x y d — частина площини де 6 4 3 12 x y z 0, 0, 0 x y z Розв’язок. Побудуємо площину, записавши її рівняння у відрізках на осях 1 2 3 4 x y z

72 знаходимо диференціал площі поверхні 2 2 61 1 1 4 16 / 9 3 x yd z z dxdy 4 4 2 3 z x y 4 4 4 61 2 4 2 2 3 3 3 D DI z x y dxdy проекцією поверхні на площину XOY є область 3 0 2, 0 3 2 D x y x 3 3 2 2 2 0 04 61 1 4 61 3 1 4 61 2 1 4 61 3 2 2 2 x x x I dx dy dx

73 Обчислення поверхневого інтеграла першого роду для неявно заданих поверхонь Нехай поверхня задана неявно рівнянням і . В цьому випадку рівність визначає єдину неявну функцію і . Тоді ( , , ) 0 F x y z 0 ( ; ; ) z. F x y z ( , , ) 0 F x y z ( , )z z x y , y x x y z y F F z z F F 2 2 21 ( , , ) x y z z Df x y z d f x y z F F F dxdy F вираз є диференціалом площі поверхні, заданої неявно 2 2 21 x y z zd F F F dxdy F (*) Під час обчислення інтеграла у правій частині рівності (*) необхідно виразити z з рівняння поверхні . ( , , ) 0 F x y z

74 Приклад. Знайти площу частини поверхні конуса , вирізаної поверхнею циліндра 2 2 2 , 0 z x y z 2 2 2 , 0 x y ax a Розв’язок: Поверхня задана неявно рівнянням . Її проекція D на площину XOY є круг 2 2 2 ( , , ) 0 F x y z 2 2 2 ( )x y ax x a y a Для обчислення площі поверхні, заданої неявно, скориста- ємось властивістю (1) та формулою (*) при . Обчислення проводимо враховуючи, що для конуса ( , , ) 1 f x y z 2 2 0 z x y 2 , 2 ; x y z. F x F y F z 2 2 2 4 4 4 2 x y z d dxdy z z

75 оскільки , то 2 2 2 ( ) 2 D D x y S d dxdy x y 2 2 z x y Подвійний інтеграл є площею круга радіусом а , і тому дорівнює a 2 D dxdy 2 2 S a

76 Двостороння гладка поверхня обхід по будь-якому замкненому контуру, що ле- жить на поверхні і не має загальних точок з її межею, не змінює напрямку нормалі до поверхні На поверхні існує замкнений контур при обході по якому напрямок нор- малі змінюється на протилежний. Це одностороння поверхня

77 Поверхневий інтеграл другого роду n r Задано кусково-гладку орієнтовану поверхню, сторо- на якої задається нормаллю де – напрямні косинуси вектора cos cosn i j k r r cos , cos , 1 n n r r На поверхні задано вектор-функцію ( , , )F x y z P x y z i Q x y z j R x y z k r r – неперервні функції( , , ), ( , , )P x y z Q x y z R x y z

78 Складемо інтегральну суму від вектор-функцій по стороні поверхні , що визначена вектором нормалі ( , , )F x y z r n r 1 1 ( ) ( ) cosn n n i i i. I F M n M P M Q M R M r r Якщо існує границя , що не залежить від способу розбиття поверхні та від вибору точок M i , то така границя називається поверхневим інтегралом другого роду від вектор-функції по стороні поверхні визначеної вктором нормалі 0 lim n. I ( , , )F x y z r n r 0 1 lim ( ) cos cos lim ( ) cos n i i i. F n d F M n M P Q R d P M Q M R M r r

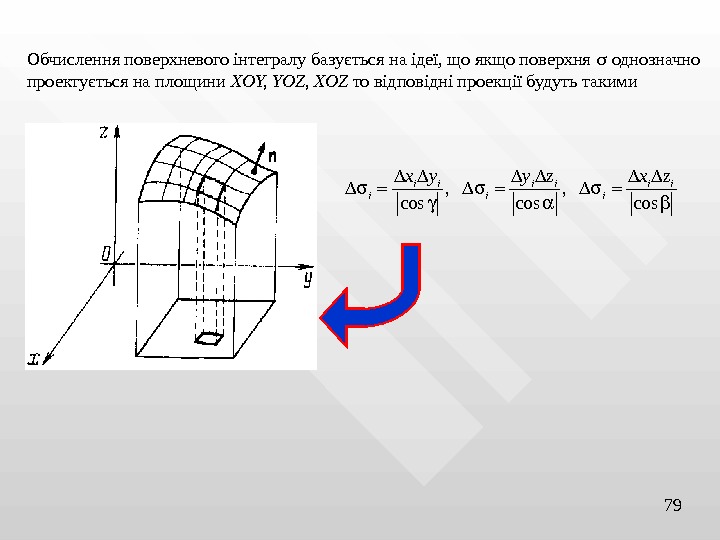
79 Обчислення поверхневого інтегралу базується на ідеї, що якщо поверхня однозначно проектується на площини XOY, YOZ, XOZ то відповідні проекції будуть такими , , cos cos i i i i i x y y z x z

801. Проектування на всі три координатні площини Якщо поверхня однозначно проектується на всі три координатні площин. Тоді рівняння поверхні однозначно розв’язується відносно кожного з аргументів x, y, z Якщо ці проекції є , то ( , , ) 0 x y z ( , ), ( , ). x x y z y y x z z z x y , , xy xz yz. D D D cos cos ( , ), , , ( , ), , , ( , ) yz xz xy D D DP Q R d P x y z dydz Q x y x z z dxdz Q x y z x y dxdy Знак перед кожним з доданків вибирається таким як знаки у , відповідно cos , cos

812. Проектування на одну із координатних площин Якщо незамкнена поверхня однозначно проектується на площину XOY в об- ласть , а рівняння поверхні можна задати як . Звідси маємо . Поверхневий інтеграл другого роду перетворюємо у подвійний інтеграл в області : xy. D ( , )z z x y cos i i i x y xy. D ( , )cos xy. D z z x y. F n d dxdy r r

82 Якщо поверхня однозначно проектується на площини XOY або YOZ , то поверх- невий інтеграл другого роду перетворюється на подвійний за формулами ( , )cos xz. D y y x z. F n d dxdz r r ( , )cos xy. D x x y z. F n d dydz r r

83 Формула Остроградського-Гаусса Якщо поверхня замкнена, а функції неперервні разом із своїми частинними похідними першого порядку в області G , обмеженою цією поверхнею, то ( , , ), ( , , )P x y z Q x y z R x y z ( , , ) GP x y z dydz Q x y z dxdz R x y z dxdy P Q R dxdydz x y z

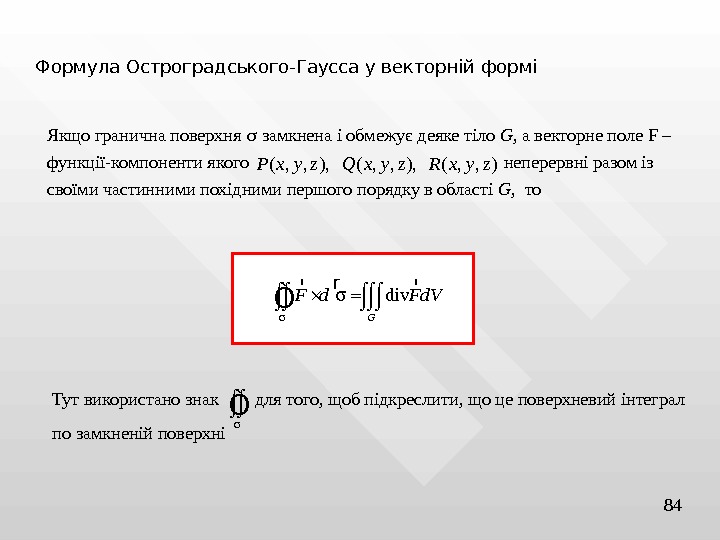
84 Формула Остроградського-Гаусса у векторній формі Якщо гранична поверхня замкнена і обмежує деяке тіло G , а векторне поле F – функції — компоненти якого неперервні разом із своїми частинними похідними першого порядку в області G , то( , , ), ( , , )P x y z Q x y z R x y z div GF d Fd. V r r r Ò Тут використано знак для того, щоб підкреслити, що це поверхневий інтеграл по замкненій поверхні Ò

85 n r. Формула Стокса Для неперервних разом із своїми похідними першого порядку функцій на кусково-гладкій поверхні , що обмежена кусково-гладкою замкненою кривою L , має місце формула Стокса ( , , ), ( , , )P x y z Q x y z R x y z L Q P Pdx Qdy Rdz dxdy x y R Q P R dydz dxdz y z z x Ñ

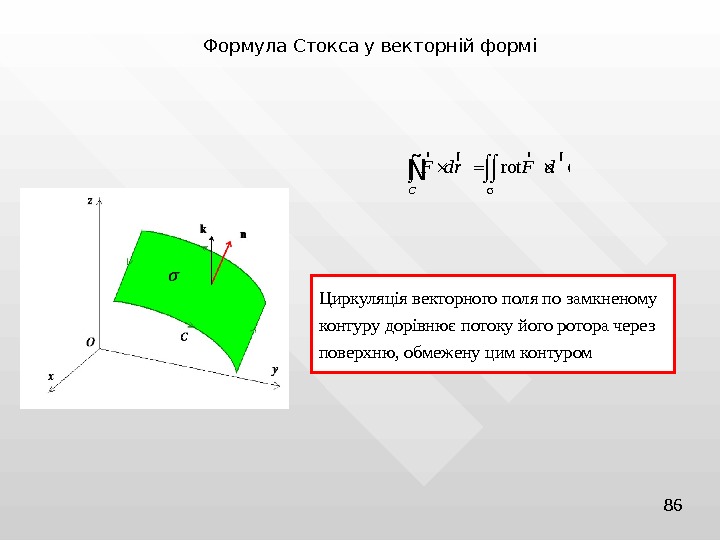
86 Формула Стокса у векторній формі rot C F dr F d r rÑ Циркуляція векторного поля по замкненому контуру дорівнює потоку його ротора через поверхню, обмежену цим контуром