Khemarak University Phnom Penh October 15 2005 Explosion

Khemarak University, Phnom Penh October 15, 2005 Explosion of Mathematics Michel Waldschmidt Université P. et M. Curie Paris VI Société Mathématique de France http: //www. math. jussieu. fr/~miw

L’explosion des Mathématiques

http: //smf. emath. fr/Publicati on/ Explosion. Des. Mathematique s/ Presentation. html

Explosion of Mathematics • • • Weather forecast Cell phones Cryptography Control theory From DNA to knot theory • Air transportation • Internet: modelisation of traffic • Communication without errors • Reconstruction of surfaces for images Société Mathématique de France Société de Mathématiques Appliquées et Industrielles

Aim: To illustrate with a few examples the usefulness of some mathematical theories which were developed only for theoretical purposes Unexpected interactions between pure research and the real world.

Interactions between physics and mathematics • Classical mechanics • Non-Euclidean geometry: Bolyai, Lobachevsky, Poincaré, Einstein • String theory • Global theory of particles and their interactions: geometry in 11 dimensions?

Eugene Wigner: « The unreasonable effectiveness of mathematics in the natural sciences » Communications in Pure and Applied Mathematics, vol. 13, No. I (February 1960)

Dynamical systems Three body problems (Henri Poincaré) Chaos theory (Edward Lorentz): the butterfly effect: Due to nonlinearities in weather processes, a butterfly flapping its wings in Tahiti can, in theory, produce a tornado in Kansas.

Weather forecast Probabilistic model for the climate Stochastic partial differential equations Statistics

Weather forecast • Mathematical models are required for describing and understanding the processes of meteorology, in order to analyze and understand the mechanisms of the climate. • Some processes in meteorology are chaotic, but there is a hope to perform reliable climatic forecast.

Knot theory in algebraic topology • Classification of knots, search of invariants • Surgical operations

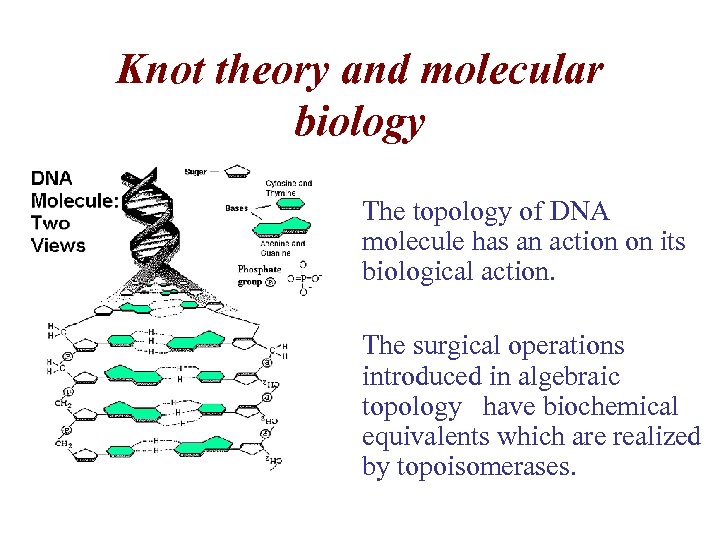
Knot theory and molecular biology • The topology of DNA molecule has an action on its biological action. • The surgical operations introduced in algebraic topology have biochemical equivalents which are realized by topoisomerases.

Finite fields and coding theory • Solving algebraic equations with radicals: Finite fields theory Evariste Galois (1811 -1832) • Construction of regular polygons with rule and compass • Group theory

Error Correcting Codes Data Transmission • • • Telephone CD or DVD Image transmission Sending information through the Internet Radio control of satellites

Olympus Mons on Mars Planet Image from Mariner 2 in 1971.

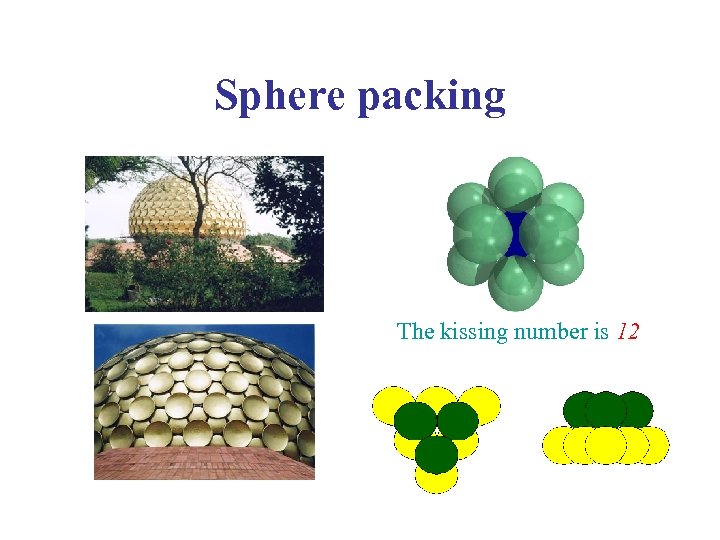
Sphere packing The kissing number is 12

Sphere Packing • Kepler Problem: maximal density of a packing of identical sphères : p / Ö 18= 0. 740 480 49… Conjectured in 1611. Proved in 1999 by Thomas Hales. • Connections with crystallography.

Codes and Geometry • 1949 Golay (specialist of radars): efficient code • Eruptions on Io (Jupiter’s volcanic moon) • 1963 John Leech: uses Golay’s ideas for sphere packing in dimension 24 - classification of finite simple groups

Data transmission French-German war of 1870, siege of Paris Flying pigeons : first crusade - siege of Tyr, Sultan of Damascus

Data transmission • James C. Maxwell (1831 -1879) • Electromagnetism

Cell Phones Information Theory Transmission by Hertz waves Algorithmic, combinatoric optimization, numerical treatment of signals, error correcting codes. How to distribute frequencies among users.

Data Transmission Source Receiver

Language Theory • Alphabet - for instance {0, 1} • Letters (or bits): 0 and 1 • Words (octets - example 0 1 0 1 0 0)

ASCII American Standard Code for Information Interchange Letters octet A: 01000001 B: 01000010 … …

Coding transmission Source Coded Text Receiver

Cryptography

Encryption for security

Applications of cryptography • Credit cards • Web security • Imaging • Encrypted television, • Telecommunications

Mathematics in cryptography • Algebra • Arithmetic, number theory • Geometry

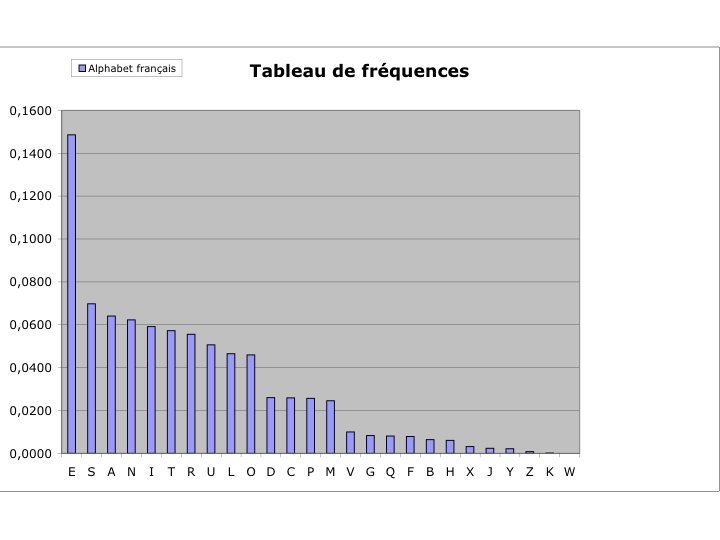
History Encryption using alphabetical transpositions and substitutions (Julius Caesar). 1586, Blaise de Vigenère (key: «table of Vigenère» ) 1850, Charles Babbage (frequency of occurrences of lettres)

Interpretation of hieroglyphs • Jean-François Champollion (1790 -1832) • Rosette stone (1799)

Any secure encyphering method is supposed to be known by the ennemy The security of the system depends only on the choice of keys. Auguste Kerckhoffs «La cryptographie militaire» , Journal des sciences militaires, vol. IX, pp. 5– 38, Janvier 1883, pp. 161– 191, Février 1883.

1917, Gilbert Vernam (disposable mask) Example: the red phone Kremlin/White House 1940, Claude Shannon proves that the only secure private key systems are those with a key at least as long as the message to be sent.

Enigma

Alan Turing Deciphering coded messages (Enigma) Computer science

Colossus Max Newman, the first programmable electronic computer (Bletchley Park before 1945)

Théorie de l’Information Claude Shannon A mathematical theory of communication Bell System Technical Journal, 1948.

Claude E. Shannon, " Communication Theory of Secrecy Systems ", Bell System Technical Journal , vol. 28 -4, page 656 --715, 1949. .

DES: Data Encryption Standard In 1970, NBS (National Board of Standards) put out a call in the Federal Register for an encryption algorithm • with a high level of security which does not depend on the confidentiality of the algorithm but only on secret keys • using secret keys which are not too large • fast, strong, cheap • easy to implement DES was approved in 1978 by NBS

Algorithm DES: combinations, substitutions and permutations between the text and the key • • • The text is split in blocks of 64 bits The blocks are permuted They are cut in two parts, right and left Repetition 16 times of permutations and substitutions One joins the left and right parts and performs the inverse permutations.

Diffie-Hellman: cryptography with public key • W. Diffie and M. E. Hellman, New directions in cryptography, IEEE Transactions on Information Theory, 22 (1976), 644 -654

RSA (Rivest, Shamir, Adleman - 1978)

R. L. Rivest, A. Shamir, and L. M. Adleman, A method for obtaining digital signatures and public-key cryptosystems, Communications of the ACM (2) 21 (1978), 120 -126

Public key Easy to multiply two numbers, even if they are large. If you know only the product, it is difficult to find the two numbers.

Example p=111395432514882798792549017547702484 4070922844843 q=191748170252450443937578626823086218 0696934189293 pq=21359870359209100823950227049996287 970510953418264174064425241650085839 57746445088405009430865999

• Quizz du malfaiteur Apprenez les maths pour devenir chef du Gang http: //www. parodie. com/monetique/hacking. htm http: //news. voila. fr/news/fr. misc. cryptologie

Primality tests • Given an integer, decide whether it is the product of two smaller numbers or not. • 8051 is composite 8051=83 97, 83 are 97 prime Today’s limit : more than 1000 digits

Industrial primes • Probabilistic Tests are not genuine primality tests: they do not garantee that the given number is prime. But they are useful whenever a small rate or error is allowed. They produce the industrial primes.

Agrawal-Kayal-Saxena • Manindra Agrawal, Neeraj Kayal and Nitin Saxena, PRIMES is in P (July 2002) http: //www. cse. iitk. ac. in/news/primality. html

Largest known primes: November 14, 2001 213 466 917 -1 4 053 946 digits November 17, 2003 220 996 011 -1 6 320 430 digits http: //primes. utm. edu/largest. html

• The 3 largest known primes can be written as 2 a -1 (and we know 40 such primes) • We know 4 primes with more than 1 000 digits, 13 primes with more than 500 000 digits, 94 primes with more than 200 000 digits

Mersenne numbers (1588 -1648) • Mersenne numbers are numbers of the form Mp=2 p -1 with p prime. • 22 944 999 -1 is composite: divisible by 314584703073057080643101377

Perfect numbers • An integer n is called perfect if n is the sum of the divisors of n distinct from n. • The divisors of 28 distinct from 28 are 1, 2, 4, 7, 14 and 28=1+2+4+7+14. • Note that 28=4 7 while 7=M 3.

Even perfect numbers (Euclid) • Even perfect numbers are numbers which can be written 2 p-1 Mp with Mp = 2 p -1 a Mersenne prime (hence p is prime). • Are-there infinitely many perfect numbers? • Nobody knows whethere exists any odd perfect numbers.

Fermat numbers (1601 -1665) • A Fermat number is a number 2 n+1. which can be written Fn=2 • Construction with rule and compass of regular polygons. • F 1=5, F 2 =17, F 3=257, F 4=65537 are prime numbers

Euler (1707 -1783) • F 5 = 232+1 is divisible by 641 4 294 967 297= 641 6 700 417 641= 54+ 24 = 5 27 + 1 • Are there infinitely many Fermat Primes?

John Cosgrave February 2003: 22 145 352 + 1 Fermat number 2 is divisible by 3 22 145 353 + 1, a prime number with 645 817 digits October 12, 2003 22 478 782 + 1 Fermat number 2 2 478 785 is divisible by 3 2 +1 a prime number with 746 190 digits www. spd. dcu. ie/johnbcos

Factorization algorithms • Given a prime number, decompose it into a product of prime numbers • Today’s limit : around 150 digits http: //www. rsasecurity. com/rsalabs/challenges/

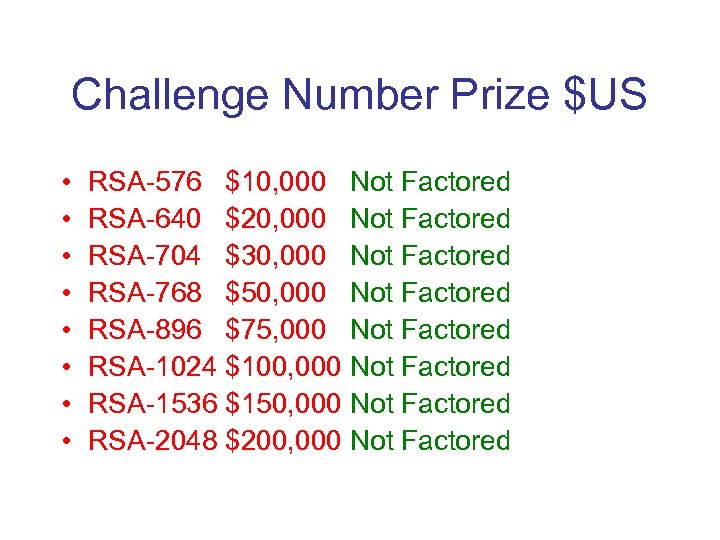
Challenge Number Prize $US • • RSA-576 $10, 000 Not Factored RSA-640 $20, 000 Not Factored RSA-704 $30, 000 Not Factored RSA-768 $50, 000 Not Factored RSA-896 $75, 000 Not Factored RSA-1024 $100, 000 Not Factored RSA-1536 $150, 000 Not Factored RSA-2048 $200, 000 Not Factored

RSA-576 Prize: $10, 000 Status: Not Factored Decimal Digits: 174 • 18819881292060796383869723946165 04398071635633794173827007633564 22988859715234665485319060606504 74304531738801130339671619969232 12057340318795506569962213051687 59307650257059 • Digit Sum: 785

21024 + 1 = 45592577 6487031809 4659775785220018543264560743076778192897 p 252 http: //discus. anu. edu. au/~rpb/F 10. html

Integers modulo n Examples: • n=2 (odd and even numbers) • n=7 (days of the week) • n=9 (sum of digits) • n=10 (keep only the last digit) • n=12 (Zodiac) • n=24 (hours) • n=60 (minutes, seconds)

Powers modulo 1000 Example: modulo 1000, keep only the last 3 digits • Start with x=111 (odd and not multiple of 5 last digit is 1, 3, 7 or 9) • x 2 =12 321 write x 2 321 mod 1000 • 111 321 =35 631 hence x 3 631 mod 1000 • Assume you know x 3 631 mod 1000 - how to recover x ? • There are 400 integers less than 1 000 which are odd and not multiple of 5.

Powers modulo 1000 (continued) • Continue to compute: x 4 41 mod 1000 • x 8 681 mod 1000 • x 16 761 mod 1000 • x 32 121 mod 1000 • x 64 641 mod 1000 • x 67 x 64 x 3 641 631 471 mod 1000 • x 201 (x 67)3 111 x mod 1000

Powers modulo 1000 (again) • The theory predicts that x 200 1 mod 1000 hence x 201 x mod 1000, x 401 x mod 1000, … • In fact computations show that already x 100 1 mod 1000

Retreive x from x 3 modulo 1000 • We know x 3 631 mod 1000 • Also x 201 x mod 1000. Notice that 201=67 3 • Hence x (x 3)67 mod 1000 67 • Compute 631 111 mod 1000 • Therefore x 111 mod 1000

Retreive x from x 7 modulo 1000 • It works if 3 is replaced by any odd number not divisible by 5 (last digit is 1, 3, 7 or 9) For instance with 7 use 1001=143 7. If you know x 7 871 mod 1000 then compute 871143 111 mod 1000 therefore x x 1001 111 mod 1000

Message modulo n • Fix a positive integer n : this is the size of the messages which are going to be sent. • All computation will be done modulo n : we replace each integer by the remainder in its division by n.

Size of n We take for n the product of two prime numbers with some 150 digits each. The product has some 300 digits: computers cannot find the two prime numbers.

Public key cryptography • Public key: (e, n) e and n are integers n gives the size of messages e is used for encryption. • Private key: f an integer, used for decryption, known only by receiver.

Choice of e, f and n • Select two large prime numbers p and q • Take n=pq. • Next select e and f such that xef x mod n for all x not divisible by p nor by q.

Cryptography with public key • The message to be sent is an integer x with 0 < x < n • The sender sends y xe mod n • The receiver computes z yf mod n Because of the choice of e and f, a miracle occurs: z x mod n.

Explanation of z x mod n • Fermat’s little theorem: If p is prime, then for any positive integer x, xp x mod p • If you know e, p and q it is easy to find f such that xef x mod n (condition: e and (p-1)(q-1) have no common factor)

Finding f • Condition on e and f: ef 1 mod (p-1)(q-1) • To compute f when one knows e, one needs to factorize p-1 and q-1. • If one knows e and n but not p and q, one is not able so far to find f.

Auxiliary questions • Send the key • Identify the sender : certification of signatures

Sending a suitcase • Assume Alice has a suitcase and a locker; she wants to send the suitcase to Bob in a secure way so that nobody can see the content of the suitcase. • Bob also has a locker and the corresponding key, but they are not compatible with Alice’s ones.

The protocol of the suitcases • Alice closes the suitcase with her locker and send it to Bob. • Bob puts his own locker and sends back the suitcase with two lockers. • Alice removes her locker and sends back the suitcase to Bob. • Finally Bob is able to open the suitcase.

Mathematical translation • The suitcase is replaced by the message x, the lockers by public keys e, the keys of the lockers by private keys f. • Alice has a public key e. A and a private key f. A. • Bob also has a public key e. B and a private key f. B. • • Alice sends to Bob x e. A modulo n. Bob sends back (x e. A ) e. B = x e. A e. B modulo n. Alice sends to Bob (x e. A e. B ) f. A = x e. B modulo n. Finally Bob computes (x e. B ) f. B = x modulo n.

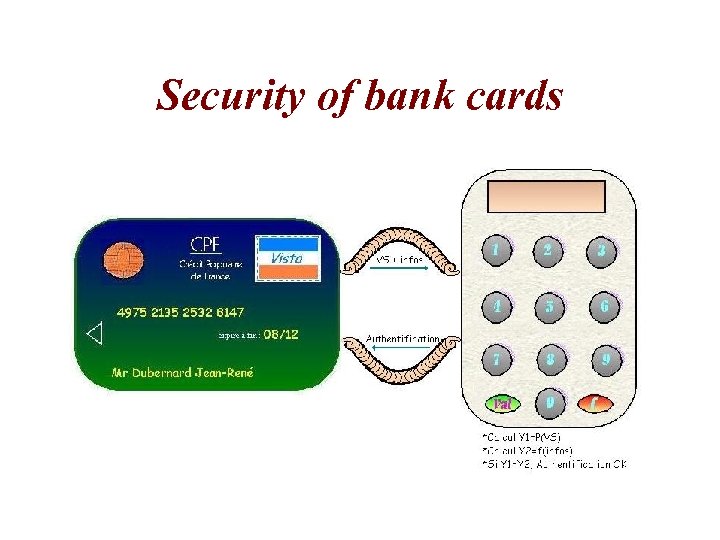
Security of bank cards

Secret code of a bank card The memory electronic card (chip card) was invented in the 70’s by two french engineers, Roland Moreno and Michel Ugon. • You need to identify yourself to the bank. You know your secret code f, but for security reason you are not going to send it to the bank. Everybody (including the bank) knows the public key e. Only you know f.

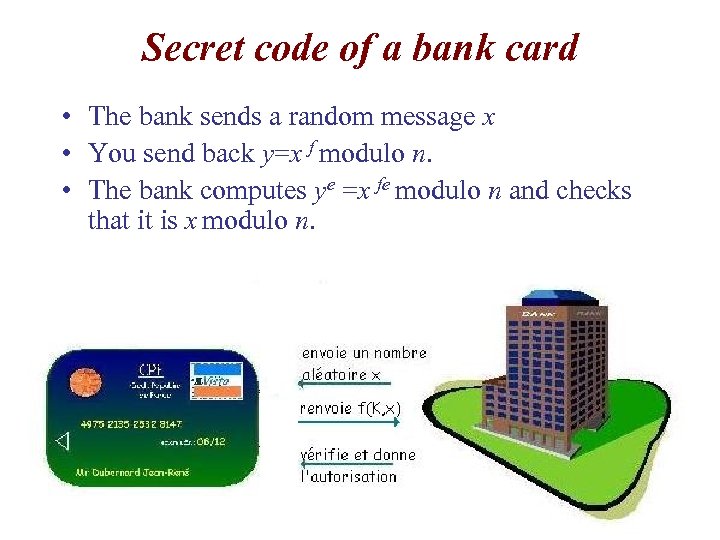
Secret code of a bank card • The bank sends a random message x • You send back y=x f modulo n. • The bank computes ye =x fe modulo n and checks that it is x modulo n.

Modern cryptography • Elliptic curves (discrete logarithm) • Jacobian of algebraic curves • Quantum cryptography (Peter Shor) - magnetic nuclear resonance

Error correcting codes

Applications of error correcting codes • Transmitions by satellites • Compact discs • Cellular phones

Codes and Maths • Algebra (discrete mathematics finite fields, linear algebra, …) • Geometry • Probability and statistics

Coding transmission Source Coded Text Receiver

Coding transmission Source Coded Text Noise Receiver

Principle of coding theory : only certain words are permitted (code = dictionary of allowed words). The « useful » letters carry the information, the other ones (control bits) allow detecting errors.

Detecting one error • Send twice the same message Code words (two letters) 0 0 1 1 2 code words on 4=22 (1 useful letter of 2) Rate: 1/2

Correcting an error • Send the same message three times Code words (three letters) 0 0 0 1 1 1 2 code words of 8=23 (1 useful letter of 3) Rate: 1/3

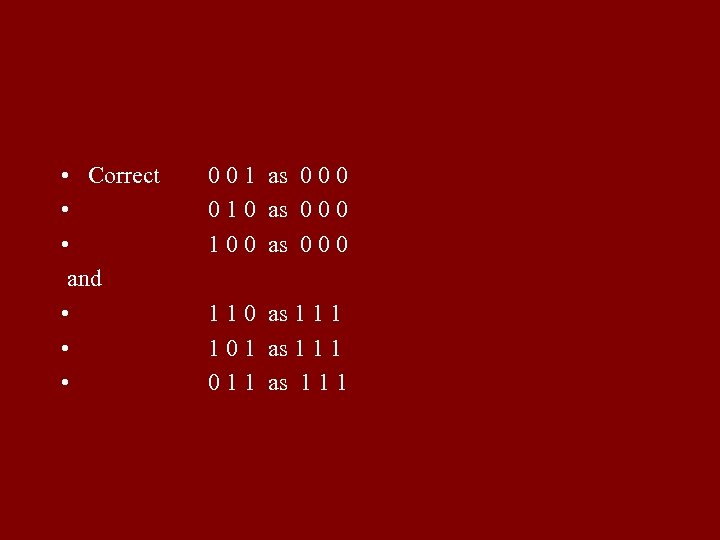
• Correct 0 0 1 as 0 0 0 • 0 1 0 as 0 0 0 • 1 0 0 as 0 0 0 and • 1 1 0 as 1 1 1 • 1 0 1 as 1 1 1 • 0 1 1 as 1 1 1

Principle of coding correcting one error: Two distinct code words have at least three distinct letters

Detecting one error (again) Code words (three letters): 0 0 1 1 1 0 Parity bit : (x y z) with z=x+y. 4=2 2=2 code words of 8=23 2 (2 useful letters of 3). Rate: 2/3

Code words Non code words 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 1 1 1 Two distinct code words have at least two distinct letters.

Correcting one error (again) Words of 7 letters Code words: (16=24 on 128=27 ) (a b c d e f g) with e=a+b+d f=a+c+d g=a+b+c Rate: 4/7

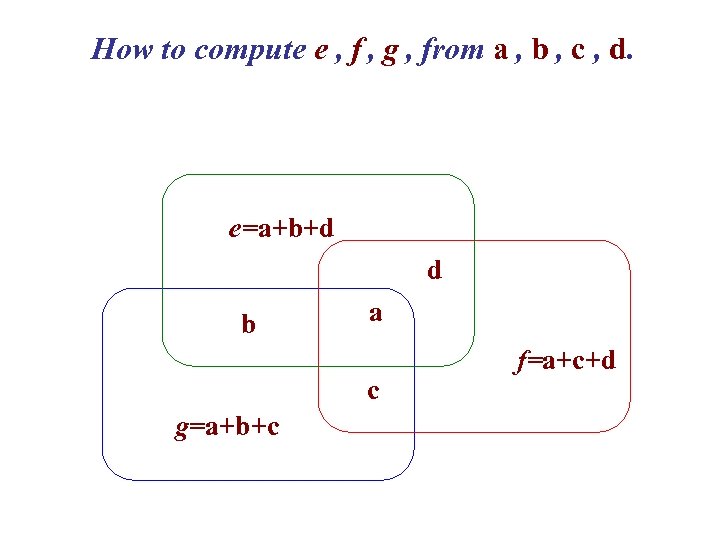
How to compute e , f , g , from a , b , c , d. e=a+b+d d b a c g=a+b+c f=a+c+d

16 code words of 7 letters 0 0 0 1 1 0 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 1 1 1 0 0 1 1 0 0 1 Two distinct code words have at least three distinct letters 1 1 0 0 1 1

Listening to a CD • On a CD as well as on a computer, each sound is coded by a sequence of 0’s and 1’s, grouped in octets • Further octets are added which detect and correct small mistakes.

Coding the sound on a CD Using a finite field with 256 elements, it is possible to correct 2 errors in each word of 32 octets with 4 control octets for 28 information octets.

A CD of high quality may have more than 500 000 errors! • 1 second of radio signal = 1 411 200 bits. • The mathematical theory of error correcting codes provides more reliability and at the same time decreases the cost. It is used also for data transmission via the internet or satellites

Informations was sent to the earth using an error correcting code which corrected 7 bits on 32. In each group of 32 bits, 26 are control bits and the 6 others contain the information.

Voyager 1 and 2 (1977) • Journey: Cape Canaveral, Jupiter, Saturn, Uranus, Neptune. • Sent information by means of a binary code which corrected 3 errors on words of length 24.

Mariner spacecraft 9 (1979) • Sent black and white photographs of Mars • Grid of 600 by 600, each pixel being assigned one of 64 brightness levels • Reed-Muller code with 64 words of 32 letters, minimal distance 16, correcting 7 errors, rate 3/16

Voyager (1979 -81) • Color photos of Jupiter and Saturn • Golay code with 4096=212 words of 24 letters, minimal distance 8, corrects 3 errors, rate 1/2. • 1998: lost of control of Soho satellite recovered thanks to double correction by turbo code.

The binary code of Hamming and Shannon (1948) It is a linear code (the sum of two code words is a code word) and the 16 balls of radius 1 with centers in the code words cover all the space of the 128 binary words of length 7 (each word has 7 neighbors (7+1) 16= 256).

The Hat Problem • A team of three people in a room with black/white hats on their head (hat colors chosen at random). Each of them sees the color on the hat of the others but not on his own. They do not communicate. • Everyone writes on a piece of paper the color he guesses for his own hat: black/white/abstain

• The team wins if at least one of the three people does not abstain, and everyone who did not abstain guesses correctly the color of his hat.

• Simple strategy: they agree that two of them abstain and the other guesses. Probability of winning: 1/2. • Is it possible to do better?

• Hint: Improve the probability by using the available information: each member of the team knows the two other colors.

• Better strategy: if a member sees two different colors, he abstains. If he sees the same color twice, he guesses that his hat has the other color.

Wins!

Loses!

Winning:

Losing:

• The team wins exactly when the three hats do not have all the same color, that is in 6 cases of a total of 8 • Probability of winning: 3/4.

• Are there better strategies? Answer: NO! • Are there other strategies giving the same probability 3/4? Answer: YES!

Tails and Ends • Throw a coin three consecutive times • There are 8 possible sequences of results: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).

If you bet (0, 1, 0), you have : • All three correct results for (0, 1, 0). • Exactly two correct results if the sequence is either (0, 1, 1), (0, 0, 0) or (1, 1, 0), • Exactly one correct result if the sequence is either (0, 0, 1), (1, 1, 1) or (1, 0, 0), • No correct result at all for (1, 0, 1).

Whatever the sequence is, among 8 possibilities, each bet is winning in exactly 1 case has exactly two correct results in 3 cases has exactly one correct result in 3 cases has no correct result at all in only 1 case

• Goal: To be sure of having at least two correct results • Clearly, one bet is not sufficient • Are two bets sufficient? Recall that there are 8 possible results, and that each bet has at least two correct results in 4 cases.

Answer: YES, two bets suffice! For instance bet (0, 0, 0) and (1, 1, 1) Whatever the result is, one of the two digits 0 and 1 occurs more than once. Hence one (and only one) of the two bets has at least two correct results.

Other solutions: • Select any two bets with all three different digits, say 0 0 1 and 1 1 0 The result either is one of these, or else has just one common digit with one of these and two common digits with the other.

• Come back with (0, 0, 0) and (1, 1, 1) The 8 sequences of three digits 0 and 1 split into two groups: those with two or three 0’s and those with two or three 1’s

Hamming Distance two words: between = number of places where the two words do not have the same letter Examples: (0, 0, 1) and (0, 0, 0) have distance 1 (1, 0, 1) and (1, 1, 0) have distance 2 (0, 0, 1) and (1, 1, 0) have distance 3 Richard W. Hamming (1915 -1998)

Hamming Distance • Recall that the Hamming distance between two words is the number of places where letters differ. • A code detects n errors iff the Hamming distance between two distinct code words is at least 2 n. • It corrects n errors iff the Hamming distance between two distinct code words is at least 2 n+1.

• The set of eight elements splits into two balls • The centers are (0, 0, 0) and (1, 1, 1) • Each of the two balls consists of elements at distance at most 1 from the center

Back to the Hat Problem • Replace white by 0 and black by 1 hence the distribution of colors becomes a word of three letters on the alphabet {0 , 1} • Consider the centers of the balls (0, 0, 0) and (1, 1, 1). • The team bets that the distribution of colors is not one of the two centers.

Assume the distribution of hats does not correspond to one of the centers (0, 0, 0) and (1, 1, 1). Then: • One color occurs exactly twice (the word has both digits 0 and 1). • Exactly one member of the team sees twice the same color: this corresponds to 0 0 in case he sees two white hats, 1 1 in case he sees two black hats. • Hence he knows the center of the ball: (0, 0, 0) in the first case, (1, 1, 1) in the second case. • He bets the missing digit does not yield the center.

• The two others see two different colors, hence they do not know the center of the ball. They abstain. • Therefore the team win when the distribution of colors does not correspond to the centers of the balls. • this is why the team win in 6 cases.

• Now if the word corresponding to the distribution of the hats is one of the centers, all members of the team bet the wrong answer! • They lose in 2 cases.

Another strategy: • Select two words with mutual distance 3 = two words with three distinct letters, say (0, 0, 1) and (1, 1, 0) • For each of them, consider the ball of elements at distance at most 1

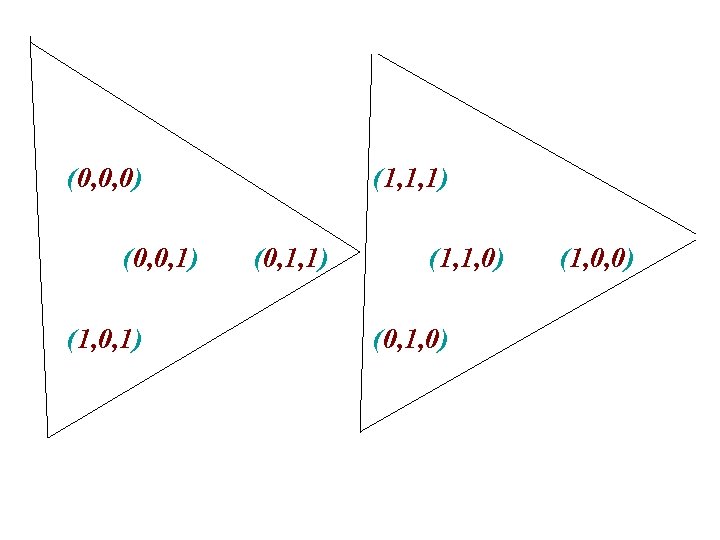
(0, 0, 0) (0, 0, 1) (1, 1, 1) (0, 1, 1) (1, 1, 0) (0, 1, 0) (1, 0, 0)

• The team bets that the distribution of colors is not one of the two centers (0, 0, 1), (1, 1, 0). • A word not in the center has exactly one letter distinct from the center of its ball, and two letters different from the other center.

Assume the word corresponding to the distribution of the hats is not a center. Then: • Exactly one member of the team knows the center of the ball. He bets the distribution does not correspond to the center. • The others do not know the center of the ball. They abstain. • Hence the team win.

The Hat Problem with 7 people • The team bets that the distribution of the hats does not correspond to the 16 elements of the Hamming code • Loses in 16 cases (they all fail) • Wins in 128 -16=112 cases (one bets correctly, the 6 others abstain) • Probability of winning: 112/128=7/8

Tossing a coin 7 times • There are 128 possible results • Each bet is a word of 7 letters on the alphabet {0, 1} • How many bets do you need if you want to guarantee at least 6 correct results?

• Each of the 16 code words has 7 neighbors (at distance 1), hence the ball of which it is the center has 8 elements. • Each of the 128 words is in exactly one of these balls.

• Make 16 bets corresponding to the 16 code words: then, whatever the result is, exactly one of your bets will have at least 6 correct answers.

The price of financial options • Probability theory yields a modelisation of random processes. The prices of stocks traded on stock exchanges fluctuate like the Brownian motion. • Optimal stochastic control involves ideas which previously occurred in physics and geometry (deformation of surfaces).

How to control a complex world • Managing distribution in an electricity network, studying the vibrations of a bridge, the flow of air around an airplane require tools from the mathematical theory of control (differential equations, partial derivatives equations). • The optimization of trajectories of satellites rely on optimal control, numerical analysis, scientific calculus, …

Optimization • • • Industry manufacturing, costs reducing, decreasing production time, … Production of fabrics, shoes : minimizing waste, … Petroleum Industry : how to find the proper hydrocarbon mixtures, … Aero dynamism (planes, cars, …). Aerospace industry : optimal trajectory of an interplanetary spaceflight, …

Mathematics involved in optimization • Algebra (linear and bilinear algebra, …) • Analysis (differential calculus, numerical analysis, …) • Probability theory.

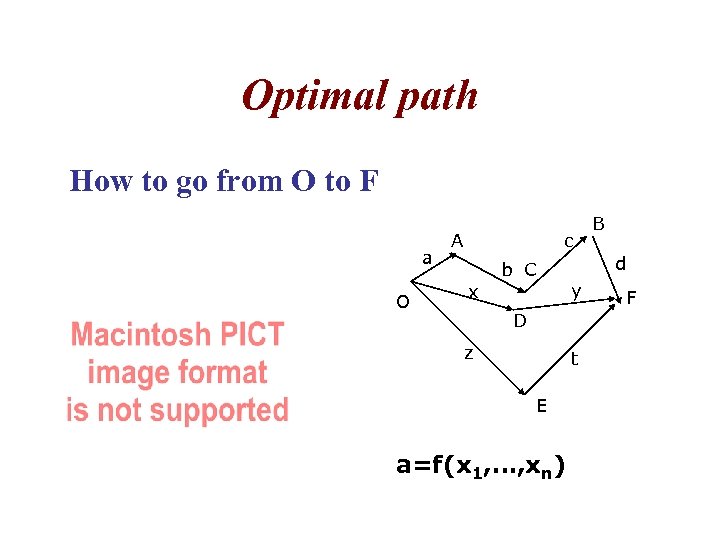
Optimal path How to go from O to F a O A c b C x d y D z t E a=f(x 1, …, xn) B F

Trees and graphs A company wants to find the best way (less expensive, fastest) for trucks which receive goods and deliver them at many different places.

Applications of graph theory • Electric circuits • How to rationalize the production methods, to improve the organization of a company. • How to manage the car traffic or the metro network. • Informatics and algorithmic • Buildings and public works • Internet, cell phones

http: //smf. emath. fr/Publicati on/ Explosion. Des. Mathematique s/ Presentation. html