3d9213c7f3e258752e5ffcde4f57a1dd.ppt
- Количество слайдов: 72
 Key Management, Message Authentication, Hash Function &
Key Management, Message Authentication, Hash Function &
 Key Management In cryptography, key management includes all of the provisions made in a cryptosystem design, in cryptographic protocols in that design, in user procedures, and so on, which are related to generation, exchange, storage, safeguarding, use, vetting, and replacement of keys. There is a distinction between key management, which concerns keys at the users' level (i. e. , passed between systems or users or both), and key scheduling which is usually taken to apply to the handling of key material within the operation of a cipher.
Key Management In cryptography, key management includes all of the provisions made in a cryptosystem design, in cryptographic protocols in that design, in user procedures, and so on, which are related to generation, exchange, storage, safeguarding, use, vetting, and replacement of keys. There is a distinction between key management, which concerns keys at the users' level (i. e. , passed between systems or users or both), and key scheduling which is usually taken to apply to the handling of key material within the operation of a cipher.
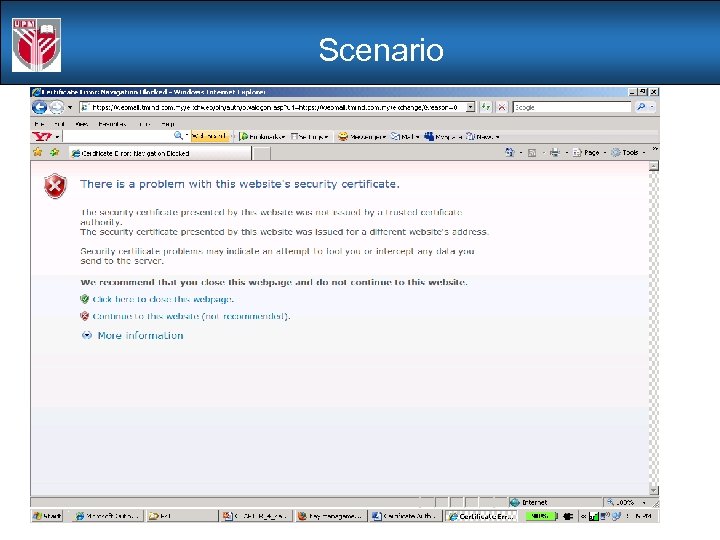 Scenario
Scenario
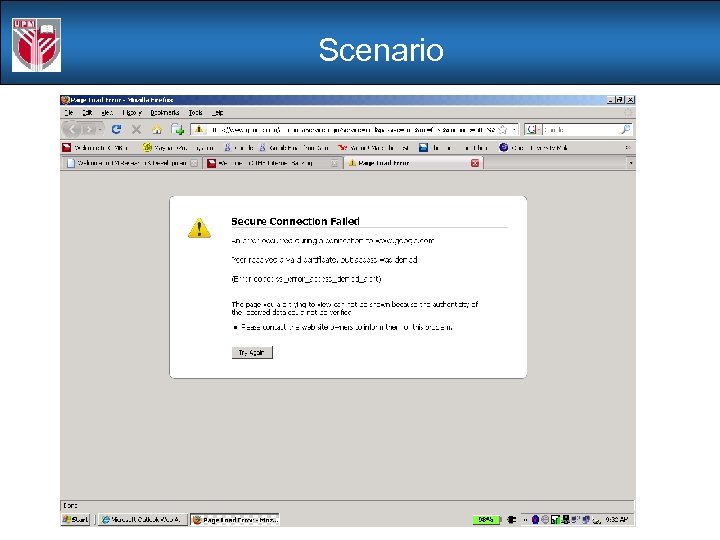 Scenario
Scenario
 KEY MANAGEMENT We never discussed how secret keys in symmetric-key cryptography and how public keys in asymmetric-key cryptography are distributed and maintained. In this section, we touch on these two issues. We first discuss the distribution of symmetric keys; we then discuss the distribution of asymmetric keys. Topics discussed in this section: Symmetric-Key Distribution Public-Key Distribution
KEY MANAGEMENT We never discussed how secret keys in symmetric-key cryptography and how public keys in asymmetric-key cryptography are distributed and maintained. In this section, we touch on these two issues. We first discuss the distribution of symmetric keys; we then discuss the distribution of asymmetric keys. Topics discussed in this section: Symmetric-Key Distribution Public-Key Distribution
 Class Discussion A small club has only 100 members. 1. How many secret keys are needed if all members of the club need to send secret messages to each other? 2. How many secret keys are needed if everyone trusts the presidents of the club? If a member needs to send a message to another member, she first sends it to president; the president then sends the message to another member. 3. How many secret keys are needed if the president decides that the two members who need to communicate should contact him first? The president then created a temporary key to be used between the two. Temporary key is encrypted and sent to both members.
Class Discussion A small club has only 100 members. 1. How many secret keys are needed if all members of the club need to send secret messages to each other? 2. How many secret keys are needed if everyone trusts the presidents of the club? If a member needs to send a message to another member, she first sends it to president; the president then sends the message to another member. 3. How many secret keys are needed if the president decides that the two members who need to communicate should contact him first? The president then created a temporary key to be used between the two. Temporary key is encrypted and sent to both members.
 Key Management on Symmetric-key
Key Management on Symmetric-key
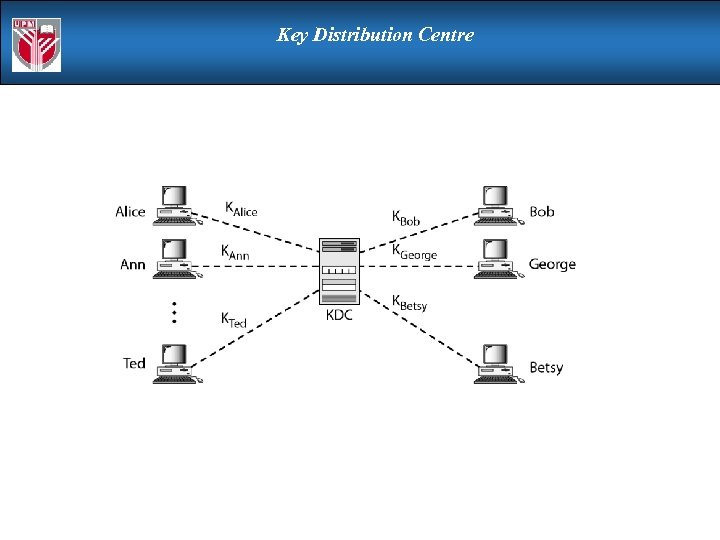 Key Distribution Centre
Key Distribution Centre
 Note A session symmetric key between two parties is used only once.
Note A session symmetric key between two parties is used only once.
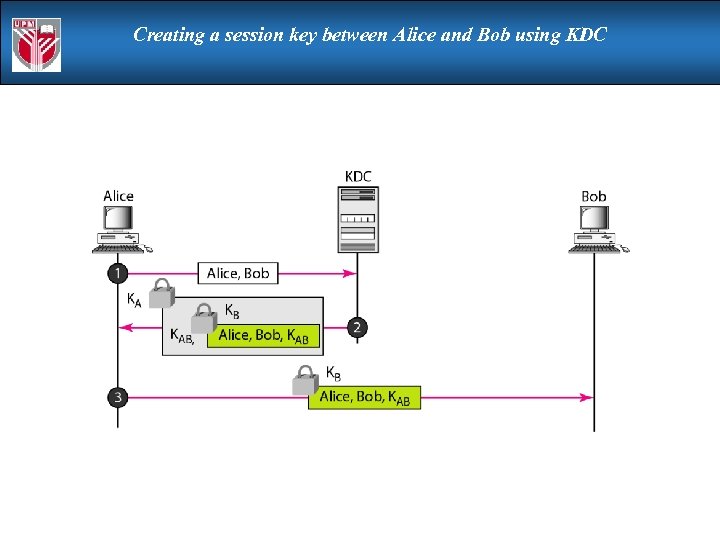 Creating a session key between Alice and Bob using KDC
Creating a session key between Alice and Bob using KDC
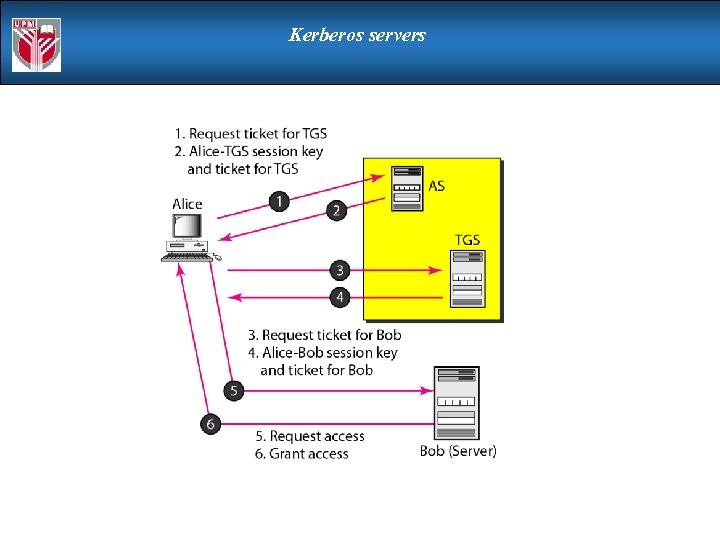 Kerberos servers
Kerberos servers
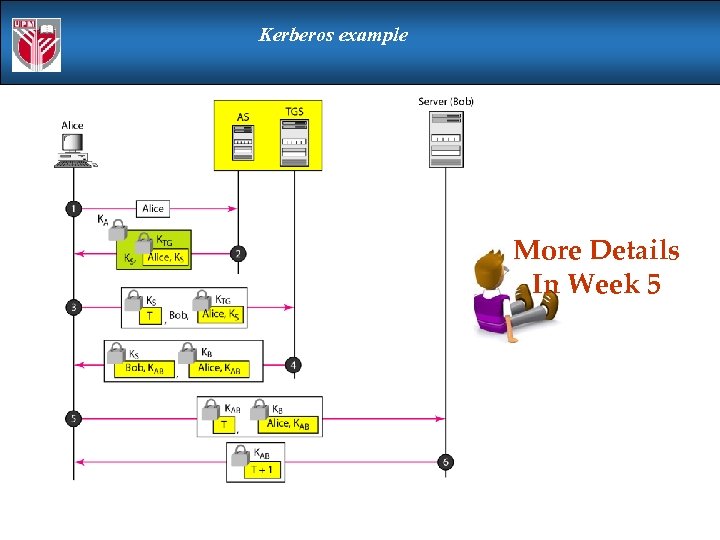 Kerberos example More Details In Week 5
Kerberos example More Details In Week 5
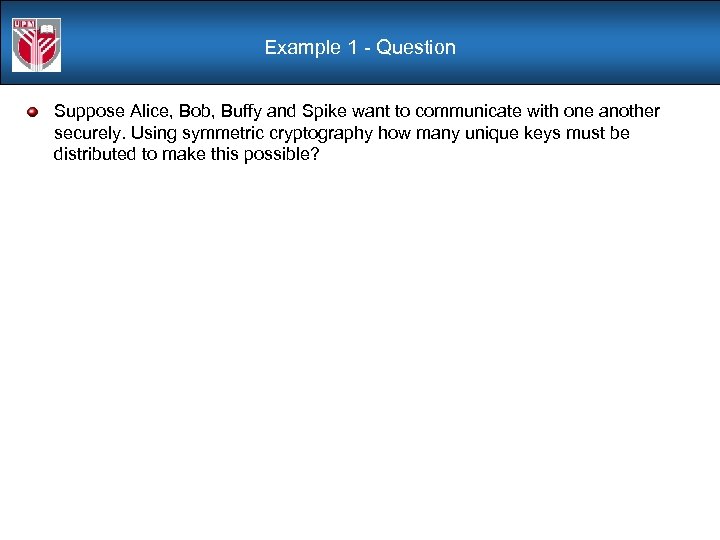 Example 1 - Question Suppose Alice, Bob, Buffy and Spike want to communicate with one another securely. Using symmetric cryptography how many unique keys must be distributed to make this possible?
Example 1 - Question Suppose Alice, Bob, Buffy and Spike want to communicate with one another securely. Using symmetric cryptography how many unique keys must be distributed to make this possible?
 Example 1 - Answer Suppose Alice, Bob, Buffy and Spike want to communicate with one another securely. Using symmetric cryptography how many unique keys must be distributed to make this possible? (Private key cryptography requires pair-wide key exchange. This is N(N-1)/2 or, in this case, 6 different keys.
Example 1 - Answer Suppose Alice, Bob, Buffy and Spike want to communicate with one another securely. Using symmetric cryptography how many unique keys must be distributed to make this possible? (Private key cryptography requires pair-wide key exchange. This is N(N-1)/2 or, in this case, 6 different keys.
 Key Management on Asymmetric-key
Key Management on Asymmetric-key
 Key Management public-key encryption helps address key distribution problems have two aspects of this: distribution of public keys use of public-key encryption to distribute secret keys This is one of the most critical areas in security systems - on many occasions systems have been broken, not because of a poor encryption algorithm, but because of poor key selection or management. It is absolutely critical to get this right!
Key Management public-key encryption helps address key distribution problems have two aspects of this: distribution of public keys use of public-key encryption to distribute secret keys This is one of the most critical areas in security systems - on many occasions systems have been broken, not because of a poor encryption algorithm, but because of poor key selection or management. It is absolutely critical to get this right!
 Note In public-key cryptography, everyone has access to everyone’s public key; public keys are available to the public.
Note In public-key cryptography, everyone has access to everyone’s public key; public keys are available to the public.
 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
 Announcing a public key / public Announcement local website newspaper
Announcing a public key / public Announcement local website newspaper
 Announcing a public key / public Announcement users distribute public keys to recipients or broadcast to community at large eg. append PGP keys to email messages or post to news groups or email list major weakness is forgery: anyone can create a key claiming to be someone else and broadcast it until forgery is discovered can masquerade as claimed user Example: Eve could make such a public announcement, before bob can react, damage could be done. Eve can fool Alice into sending her message that is intended for Bob. Eve could also sign a document with a corresponding forged private key and make everyone believe it was assigned by Bob. The approach is also vulnerable if Alice directly request Bob’s public key. Eve can intercept Bob’s response and substitute her own forged public key for Bob’s public key.
Announcing a public key / public Announcement users distribute public keys to recipients or broadcast to community at large eg. append PGP keys to email messages or post to news groups or email list major weakness is forgery: anyone can create a key claiming to be someone else and broadcast it until forgery is discovered can masquerade as claimed user Example: Eve could make such a public announcement, before bob can react, damage could be done. Eve can fool Alice into sending her message that is intended for Bob. Eve could also sign a document with a corresponding forged private key and make everyone believe it was assigned by Bob. The approach is also vulnerable if Alice directly request Bob’s public key. Eve can intercept Bob’s response and substitute her own forged public key for Bob’s public key.
 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
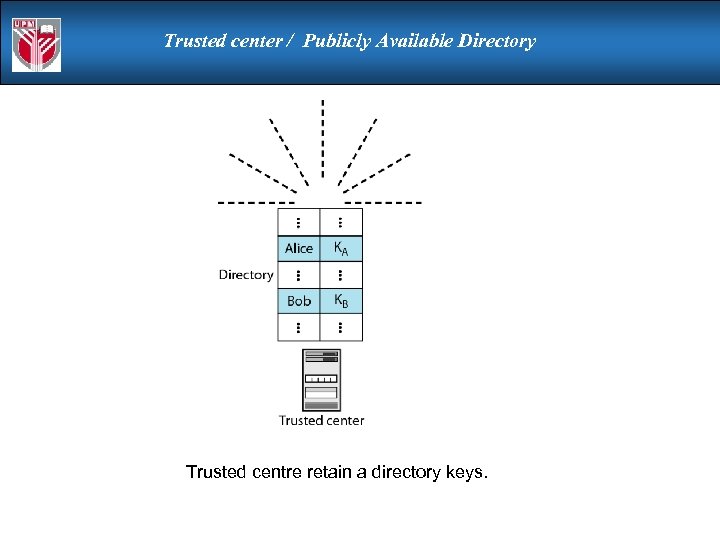 Trusted center / Publicly Available Directory Trusted centre retain a directory keys.
Trusted center / Publicly Available Directory Trusted centre retain a directory keys.
 Trusted center / Publicly Available Directory can obtain greater security by registering keys with a public directory must be trusted with properties: contains {name, public-key} entries participants register securely with directory participants can replace key at any time directory is periodically published directory can be accessed electronically still vulnerable to tampering or forgery
Trusted center / Publicly Available Directory can obtain greater security by registering keys with a public directory must be trusted with properties: contains {name, public-key} entries participants register securely with directory participants can replace key at any time directory is periodically published directory can be accessed electronically still vulnerable to tampering or forgery
 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
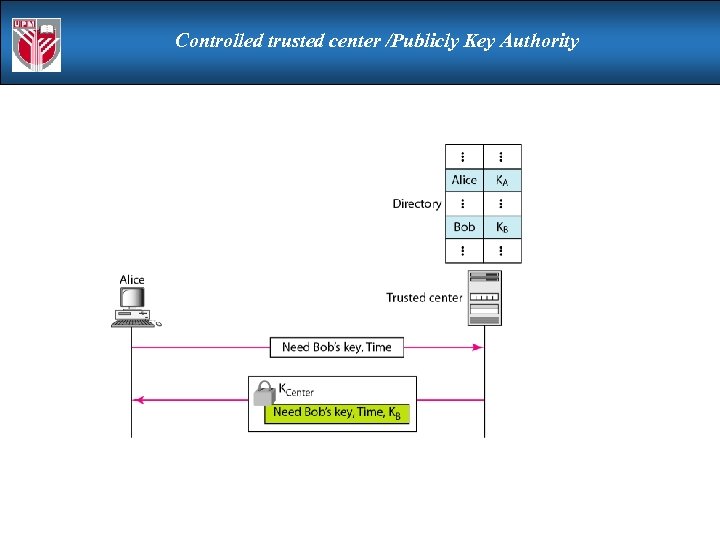 Controlled trusted center /Publicly Key Authority
Controlled trusted center /Publicly Key Authority
 Controlled trusted center /Publicly Key Authority improve security by tightening control over distribution of keys from directory has properties of directory and requires users to know public key for the directory then users interact with directory to obtain any desired public key securely does require real-time access to directory when keys are needed
Controlled trusted center /Publicly Key Authority improve security by tightening control over distribution of keys from directory has properties of directory and requires users to know public key for the directory then users interact with directory to obtain any desired public key securely does require real-time access to directory when keys are needed
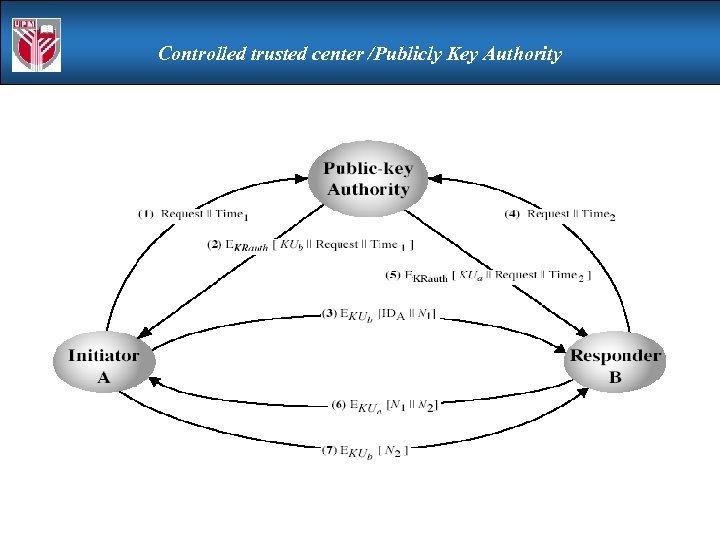 Controlled trusted center /Publicly Key Authority
Controlled trusted center /Publicly Key Authority
 Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
Distribution of Public Keys can be considered as using one of: Public announcement Publicly available directory Public-key authority Public-key certificates
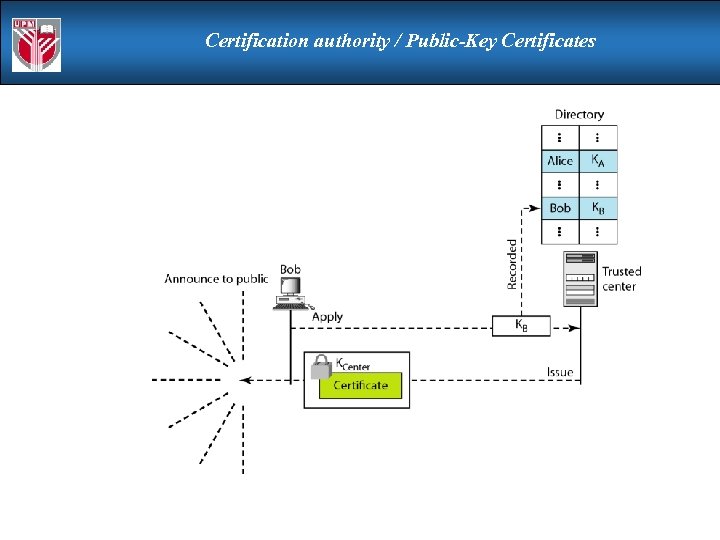 Certification authority / Public-Key Certificates
Certification authority / Public-Key Certificates
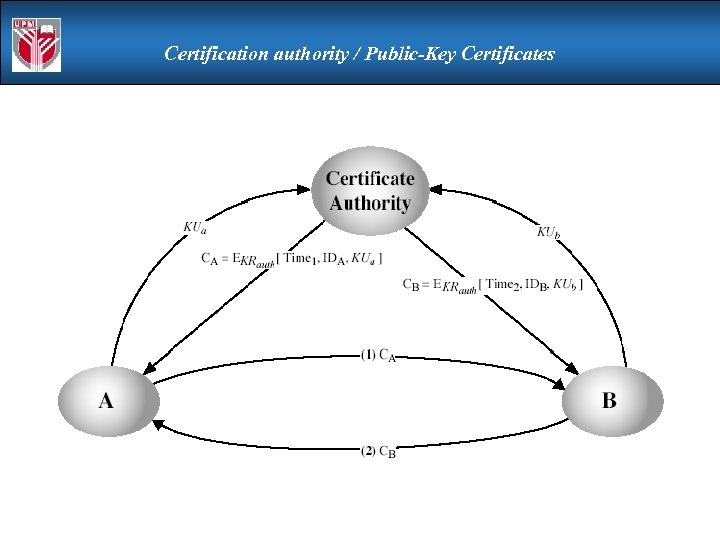
 Certification authority / Public-Key Certificates certificates allow key exchange without real-time access to publickey authority a certificate binds identity to public key usually with other info such as period of validity, rights of use etc with all contents signed by a trusted Public-Key or Certificate Authority (CA) can be verified by anyone who knows the public-key authorities public-key
Certification authority / Public-Key Certificates certificates allow key exchange without real-time access to publickey authority a certificate binds identity to public key usually with other info such as period of validity, rights of use etc with all contents signed by a trusted Public-Key or Certificate Authority (CA) can be verified by anyone who knows the public-key authorities public-key
 Certification authority / Public-Key Certificates
Certification authority / Public-Key Certificates
 Public-Key Distribution of Secret Keys use previous methods to obtain public-key can use for secrecy or authentication but public-key algorithms are slow so usually want to use private-key encryption to protect message contents hence need a session key have several alternatives for negotiating a suitable session
Public-Key Distribution of Secret Keys use previous methods to obtain public-key can use for secrecy or authentication but public-key algorithms are slow so usually want to use private-key encryption to protect message contents hence need a session key have several alternatives for negotiating a suitable session
 Simple Secret Key Distribution proposed by Merkle in 1979 A generates a new temporary public key pair A sends B the public key and their identity B generates a session key K sends it to A encrypted using the supplied public key A decrypts the session key and both use problem is that an opponent can intercept and impersonate both halves of protocol
Simple Secret Key Distribution proposed by Merkle in 1979 A generates a new temporary public key pair A sends B the public key and their identity B generates a session key K sends it to A encrypted using the supplied public key A decrypts the session key and both use problem is that an opponent can intercept and impersonate both halves of protocol
 Simple Secret Key Distribution Simple use of public-key encryption to establish a session key. 1. A generates a public/private key pair {PUa, PRa} and transmits a message to B consisting of PUa and an identifier of A, IDA. 2. B generates a secret key, Ks, and transmits it to A, encrypted with A's public key. 3. A computes D(PRa, E(PUa, Ks)) to recover the secret key. Because only A can decrypt the message, only A and B will know the identity of Ks. 4. A discards PUa and PRa and B discards PUa.
Simple Secret Key Distribution Simple use of public-key encryption to establish a session key. 1. A generates a public/private key pair {PUa, PRa} and transmits a message to B consisting of PUa and an identifier of A, IDA. 2. B generates a secret key, Ks, and transmits it to A, encrypted with A's public key. 3. A computes D(PRa, E(PUa, Ks)) to recover the secret key. Because only A can decrypt the message, only A and B will know the identity of Ks. 4. A discards PUa and PRa and B discards PUa.
 Public-Key Distribution of Secret Keys if have securely exchanged public-keys:
Public-Key Distribution of Secret Keys if have securely exchanged public-keys:
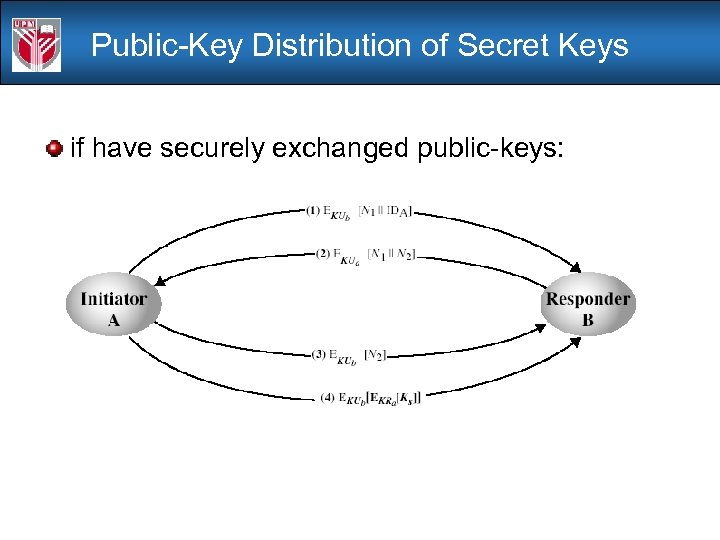
 Public-Key Distribution of Secret Keys if have securely exchanged public-keys: 1. A uses B's public key to encrypt a message to B containing an identifier of A (IDA) and a nonce (N 1), which is used to identify this transaction uniquely. 2. B sends a message to A encrypted with PUa and containing A's nonce (N 1) as well as a new nonce generated by B (N 2) Because only B could have decrypted message (1), the presence of N 1 in message (2) assures A that the correspondent is B. 3. A returns N 2 encrypted using B's public key, to assure B that its correspondent is A. 4. A selects a secret key Ks and sends M = E(PUb, E(PRa, Ks)) to B. Encryption of this message with B's public key ensures that only B can read it; encryption with A's private key ensures that only A could have sent it. 5. B computes D(PUa, D(PRb, M)) to recover the secret key.
Public-Key Distribution of Secret Keys if have securely exchanged public-keys: 1. A uses B's public key to encrypt a message to B containing an identifier of A (IDA) and a nonce (N 1), which is used to identify this transaction uniquely. 2. B sends a message to A encrypted with PUa and containing A's nonce (N 1) as well as a new nonce generated by B (N 2) Because only B could have decrypted message (1), the presence of N 1 in message (2) assures A that the correspondent is B. 3. A returns N 2 encrypted using B's public key, to assure B that its correspondent is A. 4. A selects a secret key Ks and sends M = E(PUb, E(PRa, Ks)) to B. Encryption of this message with B's public key ensures that only B can read it; encryption with A's private key ensures that only A could have sent it. 5. B computes D(PUa, D(PRb, M)) to recover the secret key.
 Public-Key Algorithms • Diffie Hellman Key-Exchange • Elliptic Curve Arithmetic • Elliptic Curve Cryptography
Public-Key Algorithms • Diffie Hellman Key-Exchange • Elliptic Curve Arithmetic • Elliptic Curve Cryptography
 Diffie-Hellman Key Exchange first public-key type scheme proposed by Diffie & Hellman in 1976 along with the exposition of public key concepts note: now know that James Ellis (UK CESG) secretly proposed the concept in 1970 is a practical method for public exchange of a secret key used in a number of commercial products
Diffie-Hellman Key Exchange first public-key type scheme proposed by Diffie & Hellman in 1976 along with the exposition of public key concepts note: now know that James Ellis (UK CESG) secretly proposed the concept in 1970 is a practical method for public exchange of a secret key used in a number of commercial products
 Diffie-Hellman Key Exchange a public-key distribution scheme cannot be used to exchange an arbitrary message rather it can establish a common key known only to the two participants value of key depends on the participants (and their private and public key information) based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
Diffie-Hellman Key Exchange a public-key distribution scheme cannot be used to exchange an arbitrary message rather it can establish a common key known only to the two participants value of key depends on the participants (and their private and public key information) based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
 Diffie-Hellman Setup all users agree on global parameters: large prime integer or polynomial q α a primitive root mod q each user (eg. A) generates their key chooses a secret key (number): x. A < q x compute their public key: y. A = α A mod q each user makes public that key y. A
Diffie-Hellman Setup all users agree on global parameters: large prime integer or polynomial q α a primitive root mod q each user (eg. A) generates their key chooses a secret key (number): x. A < q x compute their public key: y. A = α A mod q each user makes public that key y. A
 Diffie-Hellman Key Exchange shared session key for users A & B is KAB: x x KAB = α A. B mod q x = y. A B mod q (which B can compute) x = y. B A mod q (which A can compute) KAB is used as session key in private-key encryption scheme between Alice and Bob if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys attacker needs an x, must solve discrete log
Diffie-Hellman Key Exchange shared session key for users A & B is KAB: x x KAB = α A. B mod q x = y. A B mod q (which B can compute) x = y. B A mod q (which A can compute) KAB is used as session key in private-key encryption scheme between Alice and Bob if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys attacker needs an x, must solve discrete log
 Diffie-Hellman Example users Alice & Bob who wish to swap keys: agree on prime q=353 and α=3 select random secret keys: A chooses x. A=97, B chooses x. B=233 compute public keys: 97 y. A=3 mod 353 = 40 (Alice) 233 y. B=3 mod 353 = 248 (Bob) compute shared session key as: x. A 97 KAB= y. B mod 353 = 248 = 160 x. B 233 KAB= y. A mod 353 = 40 = 160 (Alice) (Bob)
Diffie-Hellman Example users Alice & Bob who wish to swap keys: agree on prime q=353 and α=3 select random secret keys: A chooses x. A=97, B chooses x. B=233 compute public keys: 97 y. A=3 mod 353 = 40 (Alice) 233 y. B=3 mod 353 = 248 (Bob) compute shared session key as: x. A 97 KAB= y. B mod 353 = 248 = 160 x. B 233 KAB= y. A mod 353 = 40 = 160 (Alice) (Bob)
 Key Management Message Authentication
Key Management Message Authentication
 Message Authentication message authentication is concerned with: protecting the integrity of a message validating identity of originator non-repudiation of origin (dispute resolution) will consider the security requirements then three alternative functions used: message encryption message authentication code (MAC) hash function
Message Authentication message authentication is concerned with: protecting the integrity of a message validating identity of originator non-repudiation of origin (dispute resolution) will consider the security requirements then three alternative functions used: message encryption message authentication code (MAC) hash function
 Security Requirements disclosure traffic analysis masquerade content modification sequence modification timing modification source repudiation destination repudiation
Security Requirements disclosure traffic analysis masquerade content modification sequence modification timing modification source repudiation destination repudiation
 Message Authentication
Message Authentication
 Message Encryption Message Authentication Code Hash Function
Message Encryption Message Authentication Code Hash Function
 Message Encryption message encryption by itself also provides a measure of authentication if symmetric encryption is used then: receiver know sender must have created it since only sender and receiver now key used know content cannot of been altered if message has suitable structure, redundancy or a checksum to detect any changes
Message Encryption message encryption by itself also provides a measure of authentication if symmetric encryption is used then: receiver know sender must have created it since only sender and receiver now key used know content cannot of been altered if message has suitable structure, redundancy or a checksum to detect any changes
 Message Encryption if public-key encryption is used: encryption provides no confidence of sender since anyone potentially knows public-key however if sender signs message using their private-key then encrypts with recipients public key have both secrecy and authentication again need to recognize corrupted messages but at cost of two public-key uses on message
Message Encryption if public-key encryption is used: encryption provides no confidence of sender since anyone potentially knows public-key however if sender signs message using their private-key then encrypts with recipients public key have both secrecy and authentication again need to recognize corrupted messages but at cost of two public-key uses on message
 Key Management Message Authentication: Message Encryption Message Authentication: Message Authentication Code Message Authentication: Hash functions
Key Management Message Authentication: Message Encryption Message Authentication: Message Authentication Code Message Authentication: Hash functions
 Cartoon Actors Alice Bob Sender Receiver Sender Eve Hacker/ Adversary Reggie Charlie Registration Authority Certification Authority 51
Cartoon Actors Alice Bob Sender Receiver Sender Eve Hacker/ Adversary Reggie Charlie Registration Authority Certification Authority 51
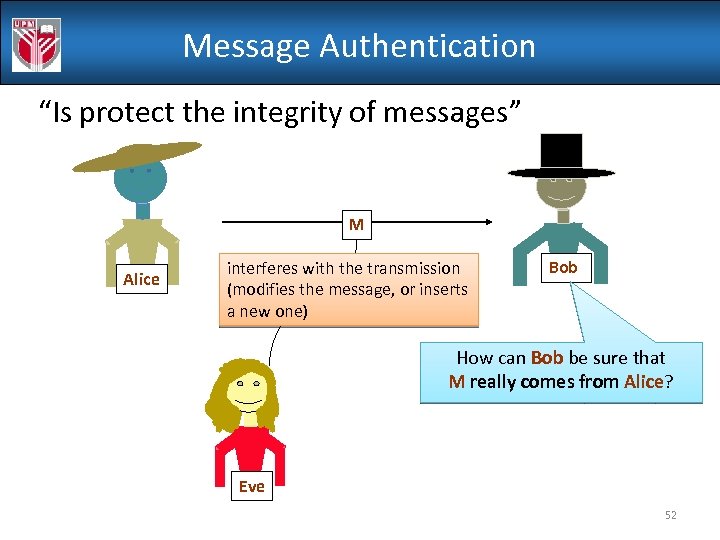 Message Authentication “Is protect the integrity of messages” M Alice interferes with the transmission (modifies the message, or inserts a new one) Bob How can Bob be sure that M really comes from Alice? Eve 52
Message Authentication “Is protect the integrity of messages” M Alice interferes with the transmission (modifies the message, or inserts a new one) Bob How can Bob be sure that M really comes from Alice? Eve 52
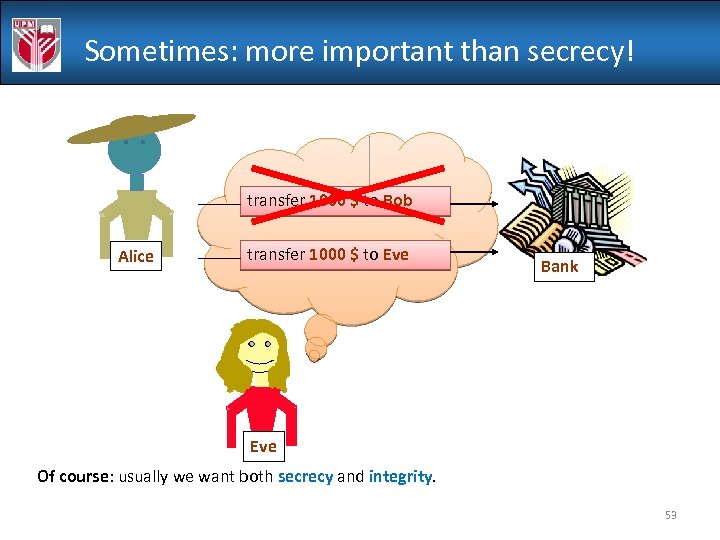 Sometimes: more important than secrecy! transfer 1000 $ to Bob Alice transfer 1000 $ to Eve Bank Eve Of course: usually we want both secrecy and integrity. 53
Sometimes: more important than secrecy! transfer 1000 $ to Bob Alice transfer 1000 $ to Eve Bank Eve Of course: usually we want both secrecy and integrity. 53
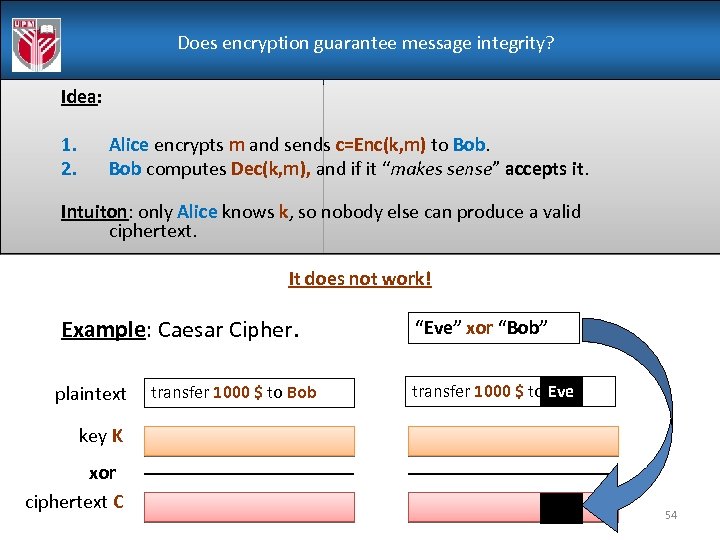 Does encryption guarantee message integrity? Idea: 1. 2. Alice encrypts m and sends c=Enc(k, m) to Bob computes Dec(k, m), and if it “makes sense” accepts it. Intuiton: only Alice knows k, so nobody else can produce a valid ciphertext. It does not work! Example: Caesar Cipher. plaintext transfer 1000 $ to Bob “Eve” xor “Bob” transfer 1000 $ to Eve key K xor ciphertext C 54
Does encryption guarantee message integrity? Idea: 1. 2. Alice encrypts m and sends c=Enc(k, m) to Bob computes Dec(k, m), and if it “makes sense” accepts it. Intuiton: only Alice knows k, so nobody else can produce a valid ciphertext. It does not work! Example: Caesar Cipher. plaintext transfer 1000 $ to Bob “Eve” xor “Bob” transfer 1000 $ to Eve key K xor ciphertext C 54
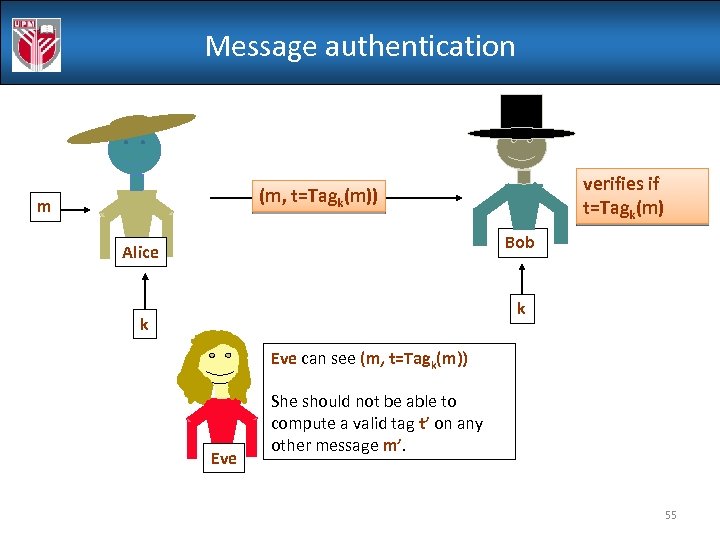 Message authentication verifies if t=Tagk(m) (m, t=Tagk(m)) m Bob Alice k k Eve can see (m, t=Tagk(m)) Eve She should not be able to compute a valid tag t’ on any other message m’. 55
Message authentication verifies if t=Tagk(m) (m, t=Tagk(m)) m Bob Alice k k Eve can see (m, t=Tagk(m)) Eve She should not be able to compute a valid tag t’ on any other message m’. 55
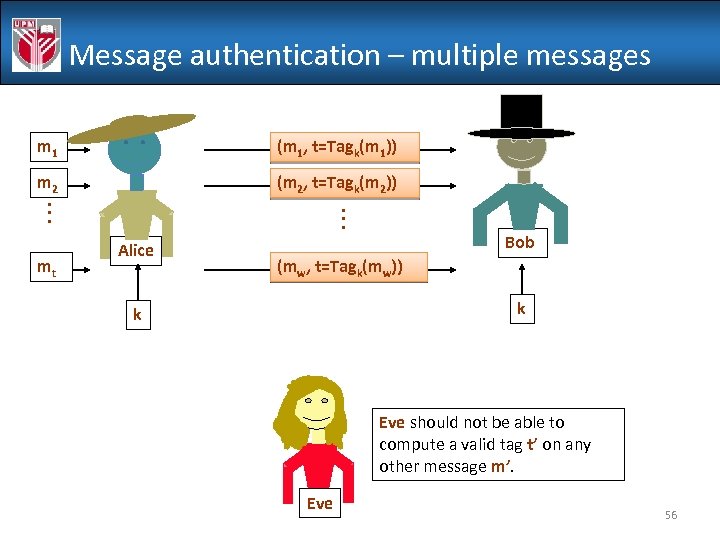 Message authentication – multiple messages m 1 (m 1, t=Tagk(m 1)) m 2 (m 2, t=Tagk(m 2)). . . mt Alice Bob (mw, t=Tagk(mw)) k k Eve should not be able to compute a valid tag t’ on any other message m’. Eve 56
Message authentication – multiple messages m 1 (m 1, t=Tagk(m 1)) m 2 (m 2, t=Tagk(m 2)). . . mt Alice Bob (mw, t=Tagk(mw)) k k Eve should not be able to compute a valid tag t’ on any other message m’. Eve 56
 Message Authentication Code (MAC) A bit string that is a function of both data (either plaintext or ciphertext) and a secret key, and that is attached to the data in order to allow data authentication. The function used to generate the message authentication code must be a one-way function. Data associated with an authenticated message allowing a receiver to verify the integrity of the message. Or other words: MAC is a short piece of information used to authenticate a message. Also, it is authentication technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC that is appended to the message.
Message Authentication Code (MAC) A bit string that is a function of both data (either plaintext or ciphertext) and a secret key, and that is attached to the data in order to allow data authentication. The function used to generate the message authentication code must be a one-way function. Data associated with an authenticated message allowing a receiver to verify the integrity of the message. Or other words: MAC is a short piece of information used to authenticate a message. Also, it is authentication technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC that is appended to the message.
 Behaviors MAC functions are similar to keyed hash functions, they posses different security requirements. MAC differ from digital signature, as MAC values are both generated and verified using the same secret key. MAC algorithms can be constructed from other cryptographic primitives, such as cryptographic hash functions (as in the case HMAC) or from block cipher algorithms (OMAC, CBC-MAC and PMAC).
Behaviors MAC functions are similar to keyed hash functions, they posses different security requirements. MAC differ from digital signature, as MAC values are both generated and verified using the same secret key. MAC algorithms can be constructed from other cryptographic primitives, such as cryptographic hash functions (as in the case HMAC) or from block cipher algorithms (OMAC, CBC-MAC and PMAC).
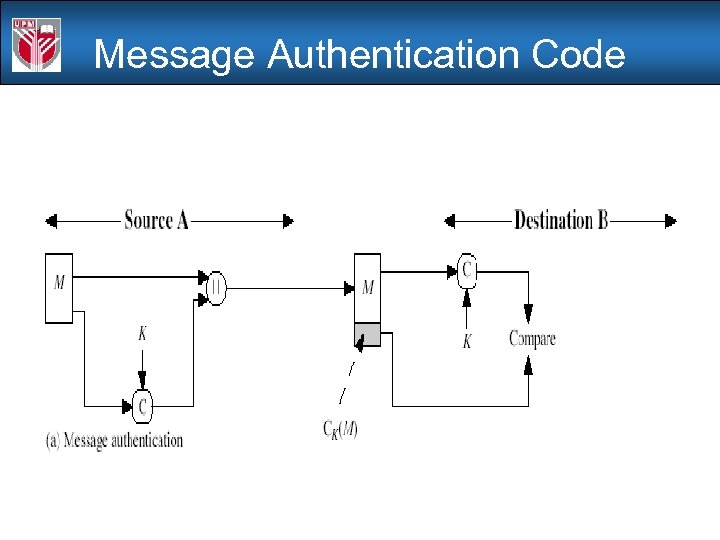
 Operations This technique assumes that two communicating parties, say A and B share a common secret key. MAC = Ck(M): M C K MAC = input message (Variable-length) = MAC function = shared secret key = message authentication code The message plus MAC are transmitted to the intended recipient. The recipient performs the same calculation on the received message, using: the same secret key: to generate a new MAC. The received MAC is compared to the calculated MAC.
Operations This technique assumes that two communicating parties, say A and B share a common secret key. MAC = Ck(M): M C K MAC = input message (Variable-length) = MAC function = shared secret key = message authentication code The message plus MAC are transmitted to the intended recipient. The recipient performs the same calculation on the received message, using: the same secret key: to generate a new MAC. The received MAC is compared to the calculated MAC.
 Operations Methods: Assume that only the receiver and the sender know the identity of the secret key. The received MAC matches the calculated MAC Therefore: The receiver is assured that the message has not been altered. The receiver is assured that the message is from the alleged sender. The sequence number is assured.
Operations Methods: Assume that only the receiver and the sender know the identity of the secret key. The received MAC matches the calculated MAC Therefore: The receiver is assured that the message has not been altered. The receiver is assured that the message is from the alleged sender. The sequence number is assured.
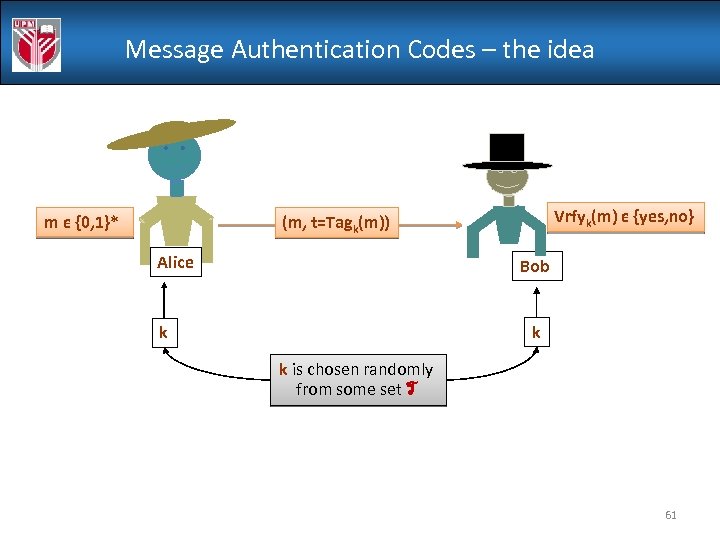 Message Authentication Codes – the idea Vrfyk(m) є {yes, no} (m, t=Tagk(m)) m є {0, 1}* Alice Bob k k k is chosen randomly from some set T 61
Message Authentication Codes – the idea Vrfyk(m) є {yes, no} (m, t=Tagk(m)) m є {0, 1}* Alice Bob k k k is chosen randomly from some set T 61
 A mathematical view K – key space M – plaintext space T - set of tags A MAC scheme is a pair (Tag, Vrfy), where Tag : K × M → T is an tagging algorithm, Ver: K × M × T → {yes, no} is an decryption algorithm. We will sometimes write Tagk(m) and Vrfyk(m, t) instead of Tag(k, m) and Vrfy(k, m, t). Correctness it should always holds that: Vrfyk(m, Tagk(m)) = yes.
A mathematical view K – key space M – plaintext space T - set of tags A MAC scheme is a pair (Tag, Vrfy), where Tag : K × M → T is an tagging algorithm, Ver: K × M × T → {yes, no} is an decryption algorithm. We will sometimes write Tagk(m) and Vrfyk(m, t) instead of Tag(k, m) and Vrfy(k, m, t). Correctness it should always holds that: Vrfyk(m, Tagk(m)) = yes.
![Message Authentication Code (MAC) MESSAGE MAC MAC Algorithm [with key (K)] MAC =? MAC Message Authentication Code (MAC) MESSAGE MAC MAC Algorithm [with key (K)] MAC =? MAC](https://present5.com/presentation/3d9213c7f3e258752e5ffcde4f57a1dd/image-63.jpg) Message Authentication Code (MAC) MESSAGE MAC MAC Algorithm [with key (K)] MAC =? MAC No Yes Authenticate Integrity Decline
Message Authentication Code (MAC) MESSAGE MAC MAC Algorithm [with key (K)] MAC =? MAC No Yes Authenticate Integrity Decline
 Message Authentication Code
Message Authentication Code
 Message Authentication Codes as shown the MAC provides confidentiality can also use encryption for secrecy generally use separate keys for each can compute MAC either before or after encryption is generally regarded as better done before why use a MAC? sometimes only authentication is needed sometimes need authentication to persist longer than the encryption (eg. archival use) note that a MAC is not a digital signature
Message Authentication Codes as shown the MAC provides confidentiality can also use encryption for secrecy generally use separate keys for each can compute MAC either before or after encryption is generally regarded as better done before why use a MAC? sometimes only authentication is needed sometimes need authentication to persist longer than the encryption (eg. archival use) note that a MAC is not a digital signature
 Requirements for MACs taking into account the types of attacks need the MAC to satisfy the following: 1. 2. 3. knowing a message and MAC, is infeasible to find another message with same MACs should be uniformly distributed MAC should depend equally on all bits of the message
Requirements for MACs taking into account the types of attacks need the MAC to satisfy the following: 1. 2. 3. knowing a message and MAC, is infeasible to find another message with same MACs should be uniformly distributed MAC should depend equally on all bits of the message
 Conventions If Vrfyk(m, t) = yes then we say that t is a valid tag on the message m. If Tag is deterministic, then Vrfy just computes Tag and compares the result. In this case we do not need to define Vrfy explicitly.
Conventions If Vrfyk(m, t) = yes then we say that t is a valid tag on the message m. If Tag is deterministic, then Vrfy just computes Tag and compares the result. In this case we do not need to define Vrfy explicitly.
 How to define security? We need to specify: 1. how the messages m 1, . . . , mw are chosen, 2. what is the goal of the adversary. Good tradition: be as pessimistic as possible! Therefore we assume that 1. 2. The adversary is allowed to chose m 1, . . . , mw. The goal of the adversary is to produce a valid tag on some m’ such that m’ ≠ m 1, . . . , mw. 68
How to define security? We need to specify: 1. how the messages m 1, . . . , mw are chosen, 2. what is the goal of the adversary. Good tradition: be as pessimistic as possible! Therefore we assume that 1. 2. The adversary is allowed to chose m 1, . . . , mw. The goal of the adversary is to produce a valid tag on some m’ such that m’ ≠ m 1, . . . , mw. 68
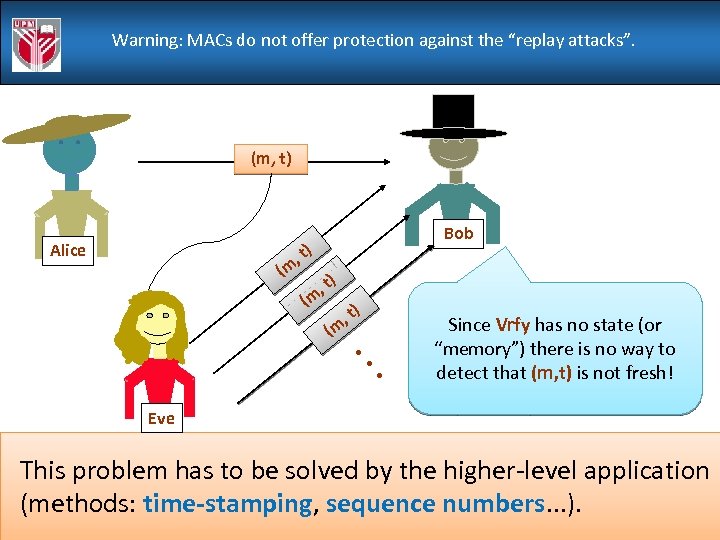 Warning: MACs do not offer protection against the “replay attacks”. (m, t) Alice , t (m Bob ) (m , t ) . . . Since Vrfy has no state (or “memory”) there is no way to detect that (m, t) is not fresh! Eve This problem has to be solved by the higher-level application (methods: time-stamping, sequence numbers. . . ). 69
Warning: MACs do not offer protection against the “replay attacks”. (m, t) Alice , t (m Bob ) (m , t ) . . . Since Vrfy has no state (or “memory”) there is no way to detect that (m, t) is not fresh! Eve This problem has to be solved by the higher-level application (methods: time-stamping, sequence numbers. . . ). 69
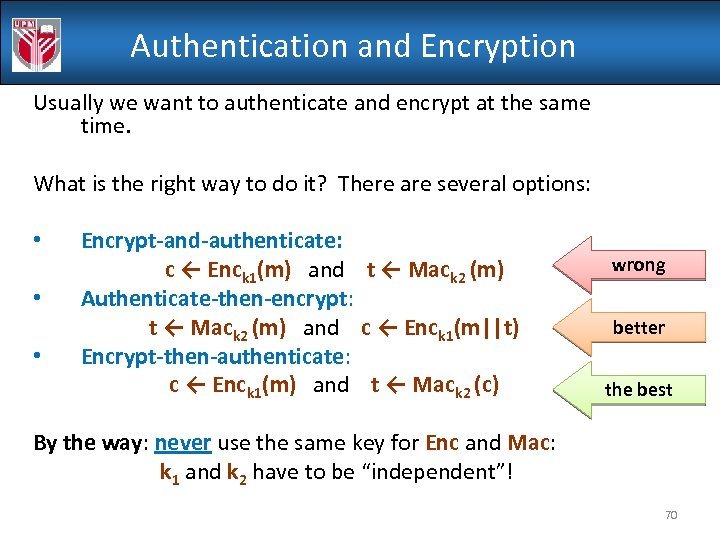 Authentication and Encryption Usually we want to authenticate and encrypt at the same time. What is the right way to do it? There are several options: • • • Encrypt-and-authenticate: c ← Enck 1(m) and t ← Mack 2 (m) Authenticate-then-encrypt: t ← Mack 2 (m) and c ← Enck 1(m||t) Encrypt-then-authenticate: c ← Enck 1(m) and t ← Mack 2 (c) wrong better the best By the way: never use the same key for Enc and Mac: k 1 and k 2 have to be “independent”! 70
Authentication and Encryption Usually we want to authenticate and encrypt at the same time. What is the right way to do it? There are several options: • • • Encrypt-and-authenticate: c ← Enck 1(m) and t ← Mack 2 (m) Authenticate-then-encrypt: t ← Mack 2 (m) and c ← Enck 1(m||t) Encrypt-then-authenticate: c ← Enck 1(m) and t ← Mack 2 (c) wrong better the best By the way: never use the same key for Enc and Mac: k 1 and k 2 have to be “independent”! 70
 Constructing a MAC 1. There exist MACs that are secure even if the adversary is infinitely-powerful. These constructions are not practical. 2. MACs can be constructed from the block-ciphers. We will now discuss to constructions: – simple (and not practical), – a little bit more complicated (and practical) – a CBC-MAC 3. MACs can also be constructed from the hash functions (NMAC, HMAC). 71
Constructing a MAC 1. There exist MACs that are secure even if the adversary is infinitely-powerful. These constructions are not practical. 2. MACs can be constructed from the block-ciphers. We will now discuss to constructions: – simple (and not practical), – a little bit more complicated (and practical) – a CBC-MAC 3. MACs can also be constructed from the hash functions (NMAC, HMAC). 71
 How Do You Want Protect Your Network System Thank You See You Next Week Have A Nice Weekend
How Do You Want Protect Your Network System Thank You See You Next Week Have A Nice Weekend


