Key-Insulated Public Key Cryptosystems Moti Yung RSA Labs

Key-Insulated Public Key Cryptosystems Moti Yung, RSA Labs and Columbia U.

Key Exposure Protection • Talk based on papers published in: EC-02 and PKC-03 (Joint work with: Y. Dodis, J. Katz and S. Xu) • Nowadays: assuming a mobile device and a host (e. g. , a home computer) is right (everyone will have/has a mobile and a computer). • Thus: we can strengthen crypto based on it! …. and derive other applications in the process…. .

Key Exposure • Most cryptosystems rely on possession of small totally secret entity (key) to perform various complex tasks. • What if the key is lost/stolen/exposed? (e. g. , mobile device, Internet, snooping)? • One of the most serious ``real-life'' attacks: – often easier to steal the key than to break the underlying “cryptography”. • Can we do anything?

Solution Approaches • Tamper-resistant hardware (smartcards). • Partial Key Exposure (weaker problem) – Secret sharing, Threshold Cryptography. – All-or-Nothing Transforms (AONT), ERF’s. • Key Evolution: change secret key over time such that exposure of “current” key minimizes the overall “damage”. – Forward security (protect past transactions) – Key-Insulated Security (this talk)

Forward Security • N periods, single public key PK • Initial Secret key SK 0 • At period i: – secret key SKi = Upd(i, SKi-1) – “effective” public key PKi = (PK, i) – Public OP done with PKi, secret OP done with SKi • Goal: under exposure of SKi, – Periods 1, …, (i-1) are still secure – Periods i, …, N are necessarily completely broken SK 0 SK 1 good … SKi-1 SKi+1 exposed … SKN bad (non-exposed)

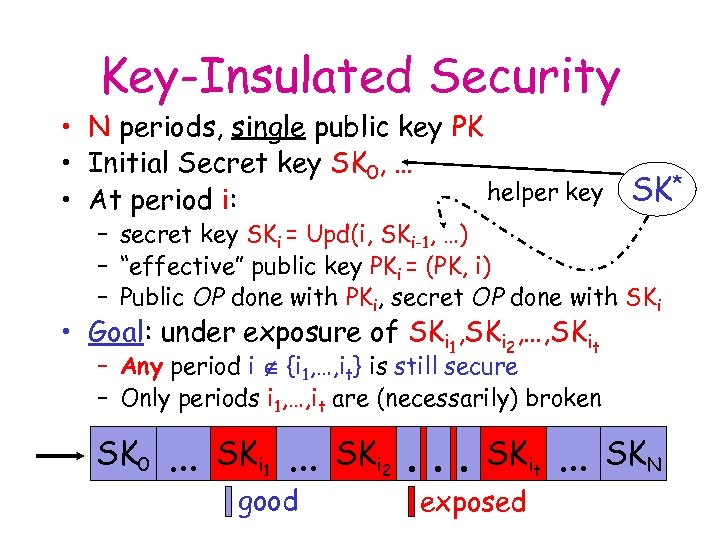
Key-Insulated Security • N periods, single public key PK • Initial Secret key SK 0, … helper key SK* • At period i: – secret key SKi = Upd(i, SKi-1, …) – “effective” public key PKi = (PK, i) – Public OP done with PKi, secret OP done with SKi • Goal: under exposure of SKi 1, SKi 2, …, SKit – Any period i {i 1, …, it} is still secure – Only periods i 1, …, it are (necessarily) broken SK 0 … SKi 1 … good SKi 2 . . . SKit exposed … SKN

High-Level Idea • Unlike forward security, user U no longer performs key updates by itself: – “Helper” H assists the user – forward-security limitation no longer applies! • All secret OPs are still done by U alone – Different from threshold/server-aided crypto! • (t, N)-security: exposure of any t secret keys leaves every non-exposed period secure • Strong (t, N)-security: H should not be able to perform any of the secret OPs (untrusted H)

More on the Model • Stronger than forward security guarantee • New: introduction of possibly untrusted H – cheap key updates: one message from H to U – All OPs by U (unlike Threshold) – H can’t compromise U (no “master” key) • Possible formalization: – Setup: (PK, SK 0, SK*), U gets SK 0, H gets SK* – SKi=Upd(SKi-1, SK*), where H sends SK* • What if Adv compromises key update? – H cannot send SK*! – SKi=Upd(SKi-1, hi), where H sends hi = Help(SK*, i)

Key Updates • Secure Key Updates: – Minimal possible harm under exposure of interperiod key-updating information (the hi’s) – Key update exposure between periods (i-1) and i key exposure at periods (i-1) and i – SKi-1 + hi (+ SKi) SKi-1 + SKi • Random Access Key Updates: – H can help go between SKj and SKi for any i, j – E. g. , emergency “future Sig” or “past Dec” – SKi=Upd(SKj, hij), where hij = Help(SK*, (j i))

The Attacker • Fully adaptive and concurrent – attacks all N periods concurrently – adaptively issues “key exposure” requests (for security against H, replaced by the knowledge of SK*) – succeeds if breaks any one of the nonexposed periods (for signature means forges a “new” message in the given period) • Typically stronger than “real life”

Brief Generic Summary • Any non-exposed period secure • All OPs done without helper • Key Updates: – Secure against inter-period exposure – Cheap and non-interactive – Random access: can go from any j to any i • Security against helper • Fully adaptive and concurrent attacker • Achieve all, but often a subset suffices

Applications • • Key Exposure Protection (original) Limited-Time Delegation assume Limited-Time Key Escrow trusted helper Identity-based Cryptography – – Users identified by “non-crypto” ID(U)=i One common public key t users can’t compromise another user Ideal: t=N-1, but smaller t often enough

Relation to ID-based Crypto • An (N-1, N)-key-insulated signature / encryption scheme is also an ID-based scheme [DKXY 02, BP 02] • Our approach based on “trapdoor primitives” encompasses all known nongeneric constructions of ID-based primitives [S 84, BF 01, CC 03, …] – Also yields new constructions (e. g. , signature based on 2 t-root/factoring assumption)

Our Results I: Signatures • Strong key-insulated signature schemes – Generic scheme based on any signature scheme – Scheme based on discrete logarithms – Most efficient: scheme based on any “trapdoor signature” scheme (similar approach works for encryption, but only one “trapdoor encryption” scheme is known)

Generic Signature Scheme • Building blocks – Any regular signature scheme • Parameters: – t=N-1, maximal resiliency – Everything constant (equal to 2 or 3) • Pretty much “optimal” uses a “certification idea” • (Like in forward security: sig. Easier than enc. ) • Morale: While we do not have full implementation of PKI, we can exploit its ideas…

Optimal Signature Scheme • PK=(VKU, VKH), SK 0=SKU, SK*=SKH • SKi= (SKU, ski, Sig. H(vki, i)) – Sig. H(vki, i) is “certificate” for (ski, vki) • Update: H sends ski, cert-I=Sig. H(vki, i) for current-period keys (ski, vki) • Signature of m at period i: (Sigvki(m), Sig. U(m, i), cert-I=Sig. H(vki, i)) • Verification: check all sigs (Note: same trick with SKU can make any key insulated signature strong)

Efficiency… • Achieves “optimal” security • (Small) slowdown: – Signing time x 2 – Verification time, signature length x 3 – Key update = 1 signing operation + 1 key generation (key generation may be costly…)

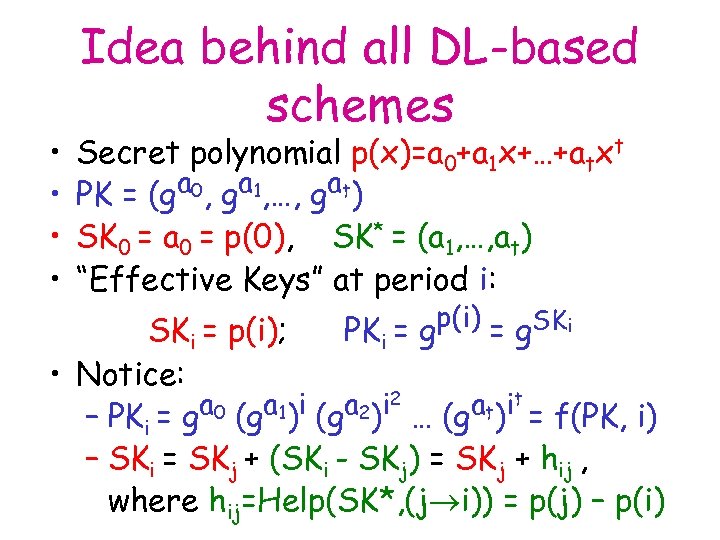
• • Idea behind all DL-based schemes Secret polynomial p(x)=a 0+a 1 x+…+atxt a 0, ga 1, …, gat) PK = (g SK 0 = a 0 = p(0), SK* = (a 1, …, at) “Effective Keys” at period i: p(i) = g. SKi PKi = g SKi = p(i); • Notice: a 0 (ga 1)i (ga 2)i 2 … (gat)it = f(PK, i) – PKi = g – SKi = SKj + (SKi - SKj) = SKj + hij , where hij=Help(SK*, (j i)) = p(j) – p(i)

Idea Continued • Take cryptosystem where pk = gsk – E. g. , Schnorr signature, El. Gamal encryption • Evolve keys as stated (functionality) • Security intuition: – For any t keys p(i 1), …, p(it), the value p(i) is truly random for i {i 1, …, it} – Helper: w/o a 0 any value p(i) is random – Hardness of discrete log ensures that ga 0, a 1, …, gat do not “help” the breaker g

Security? • Thm: for fixed {i 1, …, it}, can’t break security at any period i {i 1, …, it} • Security means: adversary cannot forge a signature in these periods (even when initially can access signing machine, cannot sign on its own a new message)

Security ? • Security against non-adaptive adversary only! – Public key is “committing”, so need to know in advance in which period to embed the “unknown discrete log” • This is unrealistic model to limit the adversary to attack at given times!

Getting Adaptive Security • Use two random generators g and h! sk = (x, y); pk = z = gx hy – 2 -generator Okamoto vs. 1 -generator Schnorr sk=x; pk=z=gx; sk=(x, y); pk=z=gxhy; Sig(m)=(gr, r-tx), Sig(m)=(grhs, r-tx, s-ty), where t=O(gr, m) where t=O(grhs, m) Ver((w, a), m) = Ver((w, a, b), m) = ? ? t g a] = [w = zt ga hb]

Getting Adaptive Security • Use two random generators g and h! sk = (x, y); pk = z = gx hy – 2 -generator Okamoto vs. 1 -generator Schnorr • Many legal ways to open the public key • Use p(x) and q(y) to evolve both keys – SKi = (xi=p(i), yi=q(i)), PKi = zi = gxi hyi • No longer decide in advance where to put the hardness: know all secret keys, reduce to hardness of computing logg h !

More Details on Key Evolution • Use two generators! • Random p(x) = a 0 + a 1 x + … + atxt and q(x) = b 0 + b 1 x + … + b tx t • Now: PK = (ga 0 hb 0, ga 1 hb 1, …, gat hbt) and SK* = (a 1, b 1, …, at, bt) • “Effective keys” for period i: SKi = (p(i), q(i)); PKi = gp(i)hq(i)

Efficiency… • Only secure against a given number t of break -ins (public-key size is O(t)) • Efficiency: – Fast key update (no cryptographic ops) – Basic signing (encrypting) time same as Okamoto. Schnorr (two-generator El. Gamal) – Has (small) overhead of computing the “period public key”, but can be done once period– (computing polynomial in the exponent trick)

Using “trapdoor” signatures • • • Say signature F has sk=x, vk=(y, ”f”), where y=f(x) and f satisfies: 1. f is easy to invert using trapdoor T 2. Given u, z, easy to verify if f(u)=z using “f” only Note, sk does not have to include T ! Examples: – – Schemes where f is a trapdoor “permutation” (Guillou-Quisquater, Fiat-Shamir, Ong-Schnorr) Recent signatures in “gap-DH” groups where DDH is easy and CDH is hard [CC 03] (all use f(ga) = gab where “f” = gb and T=b)

Using “trapdoor” signatures • Set global PK=“f”, SK*=T, vki=RO(i) • H sends ski = f-1(vki) (computed using T) to U, who uses (ski, vki) for period i • To get strong security, distribute T and jointly compute ski = f-1(vki) – Easy for most common schemes • Same approach is used in current identity-based schemes[S 84, BF 01, CC 03]

Efficiency • As efficient as the underlying signature (encryption) scheme • Achieves optimal security in RO model • Drawback: only works for specific assumptions

Our Results II: Encryption • Key-insulated public-key encryption – (t, N)-security from any semantically-secure encryption scheme – Can extend to (t, N)-CCA 2 -security – Efficient (t, N)-security based on DDH – (t, N)-CCA 2 -security based on DDH – All schemes are strong and have secure key updates /random access key updates – Also: third scheme based on BF 01….

Preliminaries • Encryption algorithm takes public key PK, period i, and message M and returns <i, C> EPK(i, M) • Decryption algorithm takes secret key SKi and ciphertext <i, C> and returns M

The Adversary • Intuitively: adversary tries to fail the encryption on any of unexposed key periods • Adversary has access to: – Key exposure oracle – Exp(i) returns SKi – Left-and-right oracle – Given a vector b = (b 1, …, b. N), oracle LRPK, b(i, M 0, M 1) returns EPK(i, Mbi)

Definition of Security • Vector b = (b 1, …, b. N) chosen at random • Adversary gets PK; asks t queries to Exp and poly-many queries to LR concurrently and adaptively • Adversary outputs (i, b’) s. t. Exp(i) not called • (t, N)-secure if | Pr[b’ = bi] – ½ | is negligible

Generic Construction • Building blocks: – Semantically-secure encryption scheme – All-or-nothing transform (AONT) – t-cover free family of sets • Parameters: – |PK| = |SK| = O(t 2 log N) – Enc. time and ciphertext length = O(t log N) – Key updating time = O(t log N) • Using the cover-free property, adversary cannot learn keys of other periods for any t corruptions.

Result • A generic scheme that works for N periods, t exposures and requires O(t 2 log N) in total, O(t log N) period. • The proof uses the fact that we use all or nothing and embeds an unknown key (in a guessed position) and breaks it if adversary is successful.

Approach for DL-Based Schemes • Idea: random p(x)=a 0 + a 1 x + … + atxt PK = (ga 0, ga 1, …, gat); SK 0 = a 0; SK* = (a 1, …, at) • “Effective keys” for period i: SKi = p(i); PKi = gp(i) = g. SKi • Notice again: PKi = ga 0 (ga 1)i (ga 2)i 2 … (gat)it SKi = SKj + (SKi - SKj) = SKj + Help(SK*, (i, j))

Approach, continued… • Now use El Gamal encryption: EPK(i, M) = <i, gr, (PKi)r M> • Intuition: – For any t keys p(i 1), …, p(it), the value p(i) is truly random for i {i 1, …, it} – Hardness of discrete log ensures that a 0, ga 1, …, gat do not “help” g

Security? • Again: only non-adaptive case…. • So not secure in the sense we want.

Adaptive Security • Again, we use two generators! …………. • Random p(x) = a 0 + a 1 x + … + atxt and q(x) = b 0 + b 1 x + … + b tx t • Now: PK = (ga 0 hb 0, ga 1 hb 1, …, gat hbt) and SK* = (a 1, b 1, …, at, bt) • “Effective keys” for period i: SKi = (p(i), q(i)); PKi = gp(i)hq(i)

Adaptive Security cont’d… • Encrypt as: EPK(i, M) = <i, gr, hr, (PKi)r M> • Decrypt via: DSKi(<i, (u, v, z)>) = z/up(i)vq(i) • Thm: Scheme achieves strong (t, N)security against adaptive adversary • Remark: Modification based on Cramer. Shoup achieves CCA 2 (security even when adversary probes the system freely with ciphertexts of its choice. )

Proof Sketch • DDH: given (g, h, u, w) decide if loggu = loghw • Use g and h, choose all secret keys, publish PK. Note: all Exp-queries can be answered! • When Adv asks LR-query (i, m 0, m 1), choose random b and return (u, w, up(i)wq(i)mb) – If loggu = loghw, perfect simulation – If u, w random, view of Adv is infotheoretically independent of b

Conclusions • Formal definition of “key-insulated” model • Many advantages over previous models • Variety of efficient implementations • Key-insulated paradigm is relevant to many algorithms and protocols – Inspired further research (e. g. , intrusion-resilient model); relation to ID-based. . • Applications to delegation, key escrow, IDbased sig. etc.

Conclusions • Cryptography should evolve as technology evolves • Cryptography should be part of a solution, even when the problem does not look “cryptographic • …and sometimes relatively efficient/ simple solutions are found… • Also…better security solution may lead to new functionality!