Key Concepts Representation Inference Semantics

Key Concepts • • • Representation Inference Semantics Discourse Pragmatics Computation

Key Concepts • Representation a formula of some logic (FOL) • Inference – constency checking task; – informativity checking • Semantics – language world

Key Concepts • Discourse – anaphora; – time; – rhetorical structure • Pragmatics – presupposition • Computation – computability – implementability

First Order Logic from a Model -Theoretic Perspective

Fundamental Syntactic Concepts • Vocabularies • First Order Languages

Vocabulary Example { (love, 2), (customer, 1), (robber, 1), (mia, 0), (vincent, 0), (honey-bunny, 0), (yolanda, 0) }

Vocabulary • Vocabularies specify the basic elements of te language we are going to use. • Items in a vocabulary associated with the number 0 are called constants. For example • Items in a vocabulary associated with a number greater than 0 are called relation symbols, (or, sometimes, predicate symbols) • For example, love is a relation symbol. In fact, it is a 2 -place relation symbol of arity 2.

First Order Languages • All symbols in the vocabulary (non-logical symbols). • An infinite collection of variables x, y, z, w, . . . • Boolean operators ¬ (negation), → (implication), ∨ (disjunction), and ∧ (conjunction). • The quantifiers ∀ (the universal quantifier) and ∃ (the existential quantifier). • The equality symbol =. • The round brackets ) and ( and the comma.

Terms • Terms are the noun phrases of firstorder languages. • All constants and variables are terms. • Nothing else is a term.

Atomic Formula • We combine our noun phrases with our predicates to form atomic formulas: • If R is a relation symbol of arity n, and τ1 , . . . , τn are terms, then R(τ1 , . . . , τn ) is an atomic (or basic) formula. • One special case of this definition is worth drawing attention to: as = is a two place relation symbol, then τ1 = τ2 is an atomic formula.

Well formed formulas • All atomic formulas are wffs • If φ and ψ are wffs then so are φ, (φ → ψ), (φ ∨ ψ), and (φ ∧ ψ) • If φ is a wff, and x is a variable, then both ∃xφ and ∀xφ are wffs (We call φ the matrix of such wffs) • Nothing else is a wff

Free and Bound Variables ( customer(x) ∨ ∀x(robber(x) ∧ ∀y person(y))) • It is useful to think of a free variable as deictic pronoun. • A sentence of first-order logic is a formula that contains no free variables.

Proof Theory • We now have a formal language • We might start by exploring syntactical patterns of inference. • In fact, the pioneers of formal logic did precisely this.

Examples • Butch is boxer and Butch is happy therefore Butch is happy φ ∧ ψ therefore φ • All boxers are brutal, Butch is boxer, therefore Butch is brutal ∀x(φ(x) → ψ(x)) φ[c/x] therefore ψ[c/x]

Model Theory • But around 1930 this syntactic view was broadened with the development of model theory, and the semantic turn • The key figure here is Alfred Tarski, a Polish logician who emigrated to the US in 1939. • He gave his celebrated satisfaction definition and thereby founded the subject that is now known as model theory.

Semantic Perspective • Language World • LOGIC MODEL

Models • In a nutshell, models are like little worlds • They are mathematical entities that first-order language talk about. • The crucial idea is to say exactly how firstorder languages talk about models, via Tarski's famous satisfaction definition • That is, we are giving a precise model concerning how first-order languages can be about something. • Tarski added aboutness.

Model: definition • A model is a pair (D, F) where • D is a domain containing the set of entities we want to talk about. It must be non-empty. • F is the interpretation function. It specifies what each symbol in the vocabulary stands for. • F associates each symbol in the vocabulary with an appropriate entity built from items in D.

Example Model • D = {d 1 , d 2 , d 3 , d 4 , d 5 } • F (mia) = d 2 F (honey-bunny) = d 1 F (vincent) = d 4 F (yolanda) = d 1 F (customer) = {d 1 , d 2 , d 4 } F (robber) = {d 3 , d 5 } F (love) = {(d 3 , d 4 )} • NB. not every entity has a name and one entity can have 2 names.

Variable Assignment Functions • Suppose we are working with a model M = (D, F ) • Then an assignment g of values to variables in M is a function from the set of variables to D • Think of g as a context which specifies values for our pronouns (free variables) • Assignment functions allows us to define satisfaction for any formula.

Interpretation of Terms • Let M = (D, F ) be a model g be an assignment of values to variables in M τ be a term • Then by the interpretation of τ with respect to M and g is meant: • F (τ ) if τ is a constant • g(τ ) if τ is a variable • We denote the interpretation of τ by Ig. F (τ ).

Satisfaction Definition M, g |= R(τ1 , · · · , τn ) iff (I(τ1 ), · · · , I(τn )) ∈ F(R) M, g |= τ1 = τ2 iff I(τ1 ) = I(τ2 ) M, g |= ¬φ iff not M, g |= φ ∧ ψ iff M, g |= φ and M, g |= ψ M, g |= φ ∨ ψ iff M, g |= φ or M, g |= ψ M, g |= φ → ψ iff not M, g |= φ or M, g |= ψ M, g |= ∃xφ iff M, g |= φ, for some x-variant g M, g |= ∀xφ iff M, g |= φ, for all x-variants g

What Does this Buy Us? • Fundamental inferential concepts – Consistency – Validity (or Noninformativity) • Framework for natural language semantics • Precise and intuitively appealing accounts of what these concepts actually are.

Consistency • A formula is consistent if it is satisfied in at least one model. • So consistent formulas describe conceivable or possible states of affairs. • For example, robber(mia) is consistent. • A formula that is not consistent is called inconsistent. So inconsistent describes inconceivable or impossible states of affairs: • robber(mia) ∧ ¬ robber(mia) is inconsistent. ･

Consistency of a Set of Formulas • A finite set of formulas {φ1 , . . . , φn } is consistent if φ1 ∧. . . ∧ φn is consistent. • A finite set of formulas that is not consistent is called inconsistent.

Validity • A valid (or uninformative) formula is a formula that is satisfied in all models (under any variable assignment) • for example: robber(mia) ∨ ¬robber(mia)). • A formula that is not valid is called invalid (or informative).

Validity • The notation |= φ means that φ is a valid formula. • The notation |/=φ means that φ is not a valid formula. That is, it means that there is at least one model in which φ is false, or to put it another way, at least one model in which ¬φ is true.

Validity of an Argument • Suppose φ1 , . . . , φn , and ψ are a finite collection of first-order sentences. • The argument with premises φ1 , . . . , φn and conclusion ψ is a valid argument if whenever all the premises are true in some model, the conclusion is true in that model also. • The notation φ1 , . . . , φn |= ψ is used to indicate a valid argument. • The notation φ1 , . . . , φn |/= ψ is used to indicate a invalid argument.

Deduction Theorem • Suppose φ1 , . . . , φn , and ψ is a finite collection of first-order sentences. Then: φ1 , . . . , φn |= ψ iff |= φ1 ∧. . . ∧ φn → ψ • DT shows that the notions of formula validity and argument validity are intimately interrelated. • DT says that an argument is valid iff the given sentence is valid.

Informativity/Validity • φ is informative (that is, not valid) if and only if ¬φ is consistent. • That is, informativity means the opposite really was an option. • φ is uninformative (that is, valid) if and only if ¬φ is inconsistent. • That is, uninformativity means that the opposite simply was not an option.

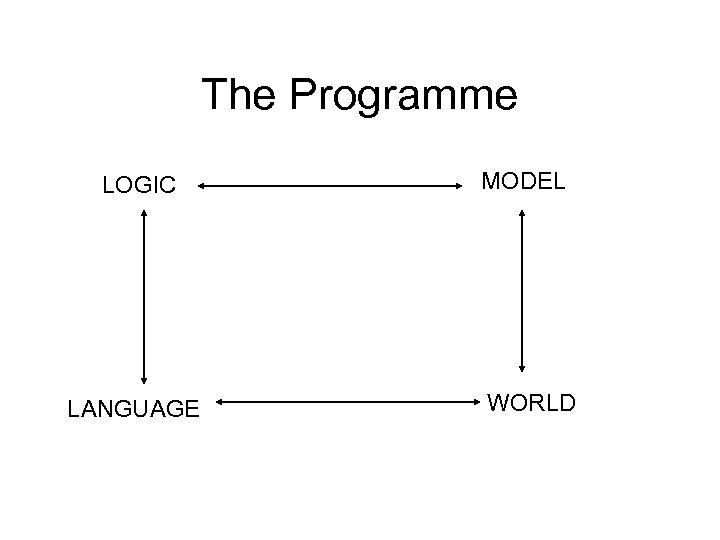The Programme LOGIC LANGUAGE MODEL WORLD

Conclusion • We have a map and a method • Much work in formal semantics can be seen as filling in aspects of this diagram • Computational semantics can be seen as giving the diagram computational content.